اثر مگنوس — از صفر تا صد

در سال 1997 میلادی، در بازی فوتبال بین دو تیم برزیل و فرانسه، تیم ملی برزیل صاحب یک ضربه مستقیم شد. روبرتو کارلوس، توپ را در فاصله 35 متری دروازه کاشت و پشت آن قرار گرفت. در حالی که بازیکنان حریف، دیوار دفاعی را به خوبی بسته بودند، این مدافع برزیلی، یکی از به یاد ماندنیترین گلهای دوران بازیگریاش را به ثمر رساند. تصویر متحرک این گل را در زیر مشاهده میکنید. در این مقاله از مجله فرادرس با معرفی اثر مگنوس پدیدههایی از این دست را تحلیل خواهیم کرد.
براساس قانون اول نیوتن، تا زمانی که نیرویی به جسم وارد نشود، سرعت و مسیر حرکت آن جسم، تغییر نخواهد کرد. وقتی بازیکنی به توپ ضربه میزند، سرعت و مسیر حرکت اولیه توپ مشخص میشود. پس در میانه راه، چه نیرویی جهت توپ را تغییر میدهد؟ پاسخ این سؤال در حرکت اسپین توپ نهفته است. هنگامی که زننده ضربه، نقطهای غیر از مرکز توپ را هدف میگیرد، توپ شروع به چرخیدن به دور محور خودش میکند. در این حالت، توپ از روی زمین بلند شده و به حرکت درمیآید. هوا در دو طرف (چپ و راست) توپ جریان دارد و رفته رفته از سرعت آن میکاهد. در یک سمت، حرکت هوا در خلاف جهت چرخش توپ است. در نتیجه، فشار افزایش مییابد. در طرف دیگر، هوا و چرخش توپ هم جهت هستند. در این ناحیه، افت فشار اتفاق میافتد. این موضوع در شکل زیر نشان داده شده است.

در ادامه، این اختلاف فشار بین دو طرف توپ به حدی میرسد که مسیر حرکت توپ به سمت ناحیه کمفشار متمایل میشود. به این پدیده، اثر مگنوس میگویند. این اتفاق در ورزشهای دیگر و با توپهایی مثل توپ بیسبال، توپ گلف و حتی فریزبی هم رخ میدهد.
تاریخچه اثر مگنوس
اثر مگنوس، ابتدا توسط نیوتن ثبت شده بود. نیوتن در سال 1672 میلادی، این اثر را به درستی در پرتاب توپ تنیس درک کرده بود. ولی «گوستاو مگنوس» (H. Gustav Magnus) فیزیکدان آلمانی، اولین کسی بود که به تشریح کامل این پدیده پرداخت.
سیالات
او در آزمایشاتش روی گلولههای شلیک شده از توپ جنگی، این موضوع را کشف کرد. شکل زیر، شماتیک آزمایشهای او روی این پرتابهها را برای توضیح اثر مگنوس نشان میدهد.

محاسبات ریاضی اثر مگنوس
با توجه به مقالههای تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد و ورتکس (Vortex) چیست؟ — به زبان ساده که پیشتر در مجله فرادرس منتشر شدهاند، این پدیده را میتوان به عنوان ترکیبی از جریان دوتایی (doublet) و ورتکس (vortex) در نظر گرفت. شکل زیر، استوانهای چرخان را در مسیر جریان نشان میدهد. در چنین شرایطی، تابع جریان را میتوان به صورت زیر نوشت.
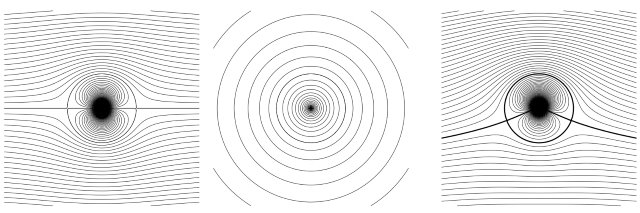
$$\large \psi = V_{\infty}r\sin\theta(1-\frac {R^2}{r^2})+\frac {\Gamma}{2\pi} \ln r$$
با محاسبه مشتق تابع جریان به طریق زیر، سرعتهای شعاعی و مماسی به دست خواهند آمد.
$$\large V_r = \frac {1}{r} \frac{\partial \psi}{\partial \theta} = V_\infty \cos\theta (1- \frac {R^2}{r^2})\\~\\
\large V_\theta = \: - \frac{\partial \psi}{\partial r} = \: - V_\infty \sin\theta (1+ \frac {R^2}{r^2}) \: - \frac {\Gamma}{2\pi r}$$
حال، سرعت و فشار را روی سطح به دست میآوریم. روی سطح استوانه، $$\large r = R$$. در نتیجه، به شیوه زیر عمل میکنیم.
$$\large V_r = 0\\~\\
\large V_\theta = \: -2V_\infty\sin\theta \: - \frac {\Gamma}{2\pi r}\\~\\
\large C_p(\theta) = 1-\frac {V^2}{V^2_\infty} = 1-4\sin^2\theta \: - (\frac {\Gamma}{2\pi V_\infty R})^2-(\frac {2\Gamma}{\pi V_\infty R})\sin \theta$$
رابطه آخر، ضریب فشار سطحی را نشان میدهد. برای به دست آوردن نیروی برآیند، باید از نیروی فشار روی سطح استوانه انتگرال بگیریم.
$$\large \overrightarrow{R} \equiv \overrightarrow{D} \hat{i} + \overrightarrow{L} \hat{j} = \huge { \oint_{} \large {-p \hat{n}dA}} $$
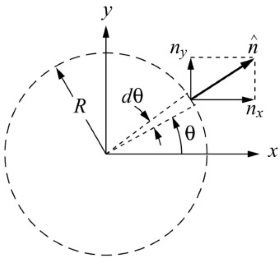
اکنون میتوانیم رابطه بالا را با توجه به شکل پایین، برحسب دو مؤلفه در جهت محورهای $$x$$ و $$y$$ بنویسیم. با تقسیم این مؤلفهها به عبارت $$\large \frac {1}{2}\rho V^2_\infty \times 2R$$ ضرایب درگ و لیفت به صورت زیر، قابل محاسبه است.
$$\large c_d = \frac {1}{2R} \oint -C_p n_x dA\\~\\
\large c_l = \frac {1}{2R} \oint -C_p n_y dA$$
با کمک هندسه استوانه، روابط زیر معلوم است.
$$\large n_x = \cos \theta, ~~~~ n_y = \sin \theta, ~~~~ dA = R d \theta$$
اکنون با کمک رابطههای بالا و جایگذاری مقدار ضریب فشار سطحی، ضرایب درگ و لیفت به شکل زیر بازنویسی میشود.
$$\large c_d = \frac {1} {2} \int_{0}^{2\pi} -C_p \cos \theta d\theta = \frac {1} {2} \int_{0}^{2\pi} [-1 + 4 \sin^2 \theta + (\frac {\Gamma} {2 \pi V_ \infty R})^2 + (\frac {2 \Gamma} { \pi V_ \infty R}) \sin \theta] \cos \theta d \theta \\~\\
\large c_l = \frac {1} {2} \int_{0}^{2\pi} -C_p \sin \theta d\theta = \frac {1} {2} \int_{0}^{2\pi} [-1 + 4 \sin^2 \theta + (\frac {\Gamma} {2 \pi V_ \infty R})^2 + (\frac {2 \Gamma} { \pi V_ \infty R}) \sin \theta] \sin \theta d \theta$$
با محاسبه دو انتگرال، مقدار این دو ضریب به دست میآید.
$$\large c_d = 0 , ~~~~~ c_l = \frac {\Gamma}{V_\infty R}$$
صفر شدن ضریب درگ در رابطه بالا، به عنوان پارادوکس دالامبر شناخته میشود. زیرا طبق مشاهدات، میدانیم به تمامی اجسام در جریان یکنواخت، همواره نیروی درگ وارد میشود. البته این اتفاق، غیر از چشمپوشی از ویسکوزیته، دلیل دیگری ندارد. با استفاده از ضریب لیفت، نیروی لیفت به صورت $$\large \rho V_\infty \Gamma$$ تعریف میشود. این نتیجه، به عنوان نظریه «کوتا - جوکوفسکی» (Kutta-Joukowsky) شناخته میشود و برای تمام اجسام دو بعدی معتبر است.
جریان واقعی روی استوانه
در جریان واقعیِ ویسکوز روی یک استوانه با عدد رینولدز بالا، جدایش جریان و نیروی درگ، بزرگ خواهد بود. در حالت عادی، جریان در بین بالا و پایین استوانه صفر است و نیروی لیفتی وارد نخواهد شد. اما اگر استوانه، سرعت زاویهای هم داشته باشد، جدایش جریان موجب به هم زدن تقارن جریان میشود. در اینجا اثر مگنوس رخ میدهد. ممکن است نیروی لیفت در این حالت، از نیروی لیفت بال هواپیما با همین اندازه هم بیشتر شود. ولی به طور همزمان، نیروی درگ بزرگی هم ایجاد شده است. همین موضوع، استفاده مثبت از نیروی لیفت را با پیچیدگی مواجه میکند.
کاربردهای دیگر اثر مگنوس
با وجود توضیحات ارائه شده، میتوان تحت شرایطی خاص، از اثر مگنوس استفاده مثبت کرد. در صنعت هوانوردی، برخی از هواپیماها برای ایجاد نیروی لیفت از اثر مگنوس استفاده میکنند. استوانهای در قسمت بال هواپیما قرار میگیرد. نیروی لیفتی که بدین طریق ایجاد میشود، به هواپیما کمک میکند با سرعت افقی کمتری پرواز کند. در برخی طراحیها، تمام بال به شکل استوانه ساخته میشود.
کشتیهای روتوری، با کمک روتورهای فلتنر از اثر مگنوس بهره میبرند. این روتورها به پاس خدمات مخترع آن، «آنتون فلتنر» (Anton Flettner) مهندس آلمانی، نامگذاری شده است. روتور فلتنر، استوانه بلندی است که حول محور طولی خود حرکت چرخشی دارد. با عبور جریان هوا از روی سطح این روتور، اثر مگنوس، نیرویی آیرودینامیکی ایجاد میکند. این نیروی آیرودینامیکی، بر محور طولی استوانه و مسیر جریان عمود است. به دلیل نصب عمودی این استوانههای بلند، نیروی لیفت ایجاد شده، به عنوان نیروی پیشرانه کشتی عمل میکند. در شکل زیر، این کاربردها را مشاهده میکنید.

در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز پیشنهاد میشوند:
- تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
- ورتکس (Vortex) چیست؟ — به زبان ساده
- جریان تراکم پذیر (Compressible Flow) — اصول و مفاهیم
^^










سلام
ببخشید استفاده از مطالب سایت با ذکر منبع برای یک ارائه ی دانشگاهی اشکال داره ؟
سلام، وقت شما بخیر؛
شرایط استفاده از مجله فرادرس را میتوانید به صورت کامل در این لینک مطالعه کنید.
از اینکه با ما همراه هستید بسیار سپاسگزاریم.
سلام اثر مگنوس با اثر برنولی چه فرقی میکند،این مگه همون نیست؟؟؟!!!!!لطفا جواب بدید ، ممنون
سلام و روز شما به خیر؛
اثر مگنوس بیان میکند که مسیر حرکت جسم در حال چرخش به گونهای منحرف میشود که این انحراف در حالت حرکت غیرچرخشی جسم وجود ندارد. این در حالی است که اثر برنولی بیان میکند که افزایش سرعت سیال همراه با کاهش فشار استاتیک یا کاهش انرژی پتانسیل سیال است. برای آشنایی بیشتر با اثر برنولی مطلب معادله برنولی — به زبان ساده را مطالعه کنید.
از اینکه با فرادرس همراه هستید خرسندیم.