آزمون کوکران Q در آمار | پیاده سازی در SPSS

یکی از انواع دادههای آماری، مقادیر طبقهای به صورت ۰ و ۱ هستند که گاهی به آن دادههای باینری نیز میگویند. تجزیه و تحلیل و انجام آزمون روی این گونه دادهها، براساس توزیعهای گسسته یا روشهای ناپارامتری صورت میگیرد. برای مثال «آزمون دوجملهای» (Binomial Test) یکی از آزمونهایی است که برای سنجش نسبت دو گروه به کار میرود. اما آزمون کوکران Q برای سنجش برابری یا یکسان بودن توزیع یا نسبت در بیش از دو گروه صورت میپذیرد. این آزمون از نوع ناپارامتری است و کمترین فرضها را در مورد جامعه آماری دارد. البته توجه داشته باشید که دادههای به کار رفته در این آزمون مانند آزمون دو جملهای، باید از نوع «دو وضعیتی» (Dichotomous) باشد. در این بین برای انجام تحلیل و اجرای آزمون، از نرمافزار محاسبات آماری SPSS استفاده کرده و در انتها نیز خروجیها را تفسیر خواهیم کرد.
به منظور آشنایی بیشتر با دادههای باینری و نحوه ورود و ثبت آنها در SPSS نوشتارهای دیگر مجله فرادرس با عنوان متغیر دو وضعیتی (Dichotomous) در SPSS — راهنمای کاربردی و جامعه آماری — انواع داده و مقیاسهای آنها را مطالعه کنید. همچنین مطالعه مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری و آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات نیز خالی از لطف نیست.
آزمون کوکران Q
در آمار، در تجزیه و تحلیل «طرحهای بلوک تصادفی دو طرفه» (two-way randomized block designs) که متغیر پاسخ میتواند تنها دو نتیجه ممکن را به همراه داشته باشد (با کد 0 و 1) از «آزمون کوکران» (Cochran's Q test) که یک «آزمون آماری ناپارامتری» (Non-parametric Test) است استفاده میشود. در حقیقت این آزمون به بررسی نسبتها در بین چندین جامعه یا یکسان بودن اثرات k تیمار میپردازد.
این آزمون به افتخار «ویلیام کوکران» (William Gemmell Cochran)، آزمون کوکران Q نامیده شده است. او این روش آزمون آماری را در مقالهای با عنوان «مقایسه درصدها در نمونههای منطبق» (The Comparison of Percentages in Matched Samples) که در سال ۱۹۵۰ در «مجله بایومتریکا» (Biometrika) منتشر کرد، معرفی و ارائه نمود و آماره آزمون را Q نامید.
نکته: آزمون کوکران Q را نباید با آزمون کوکران C که یک آزمون واریانس «نقاط دورافتاده» (Outlier) است، اشتباه گرفت.
به زبان ساده، آزمون کوکران Q، مستلزم این است که فقط یک متغیر پاسخ با مقادیر باینری (یا دو وضعیتی) وجود داشته باشد. به عنوان مثال موفقیت/شکست یا 1/0، نمونههایی از مقادیر متغیر پاسخ دو وضعیتی هستند. از طرفی این مقادیر باید برای بیش از دو گروه از تیمارها، ثبت شده باشد. این آزمون ارزیابی میکند که آیا نسبت موفقیت (که معمولا نامیده میشود) در بین گروهها یا تیمارها، یکسان است یا خیر. غالباً از این روش برای ارزیابی اینکه آیا داورانی که در مورد یک پدیده نظر ارائه کردهاند، دیدگاه یکسانی دارند یا خیر. به این ترتیب سازگاری در نظرات و درصدهای اخذ شده، مورد بررسی قرار میگیرد.
طرح بلوک تصادفی و آزمون کوکران Q
همینطور که گفته شد، اگر تعداد تیمارها روی آزمودنیها، بیشتر از ۲ تیمار باشد، آزمون کوکران Q مناسب خواهد بود. در طرح آزمایشات چنین آزمونی، یک بلوک تصادفی به صورت زیر را در نظر میگیریم.
جدول طرح بلوکی برای تیمار و بلوک تصادفی
| شماره بلوک | تیمار ۱ | تیمار ۲ | تیمار k |
| بلوک ۱ | |||
| بلوک ۲ | |||
| بلوک b |
در ادامه بر اساس خانههای این جدول، آماره آزمون و توزیع آن معرفی میشود.
آماره آزمون کوکران Q
طبق طرح جدول بالا، آماره آزمون کوکران Q بر حسب مجموع سطرها و ستونها، به صورت زیر محاسبه میشود. توجه داشته باشید که مقادیر به صورت ۰ و ۱ هستند.
که در آن منظور از ، تعداد تیمارها و نیز تعداد بلوکها است. از طرفی به معنی مجموع ستون برای تیمار ام و نیز جمع سطر برای بلوک ام است. واضح است که جمع کل نیز برابر با (تعداد ۱ها) خواهد بود.
فرض صفر در آزمون کوکران Q یکسان بودن اثر تیمارها است. در فرض مقابل نیز اختلاف در اثر تیمارها قرار گرفته است. به این ترتیب در صورتی که فرض صفر رد شود، مشخص خواهد شد که حداقل یکی از تیمارها با بقیه متفاوت است.
به این ترتیب، زمانی که صورت کسر بزرگ باشد، مشخص است که تیمارها با یکدیگر اختلاف دارند و فرض صفر رد میشود. و برعکس کوچک بودن آن، نشانگر یکسان بودن اثر تیمارها خواهد بود. به منظور تعیین ناحیه بحرانی برای چنین آمارهای، باید توزیع آن و همینطور سطح آزمون را مشخص کنیم. آماره آزمون کوکران Q به صورت مجانبی دارای توزیع کای ۲ با درجه آزادی است. ناحیه بحرانی برای این آزمون به صورت نوشته میشود. میدانید که صدک توزیع کای ۲ با درجه آزادی است.
بنابراین اگر مقدار آماره آزمون بیشتر از صدک ام توزیع کای ۲ باشد، فرض صفر رد خواهد شد. در این صورت برای مشخص کردن عامل اختلاف، احتیاج به «آزمونهای مقایسه چندگانه» (Multiple Comparisons) یا «آزمونهای تعقیبی» (Post-Hoc) است.
نکته: توزیع دقیق آماره آزمون در صورتی که تعداد نمونهها کوچک باشد قابل محاسبه است. در این صورت از مقدار بحرانی دقیق استفاده میشود ولی به دلیل پیچیدگی محاسباتی کمتر برای آزمون به کار میآید.
پیشفرضهای آزمون کوکران Q
آزمون کوکران Q بر اساس مفروضات زیر محاسبه و عمل میکند.
- اگر از تقریب نمونه بزرگ استفاده شود (و نه توزیع دقیق)، لازم است که مقدار بزرگ انتخاب شود.
- بلوکها به طور تصادفی از جمعیت تمام بلوکهای ممکن انتخاب شدند.
- نتایج تیمارها را باید به صورت پاسخهای دودویی کدگذاری کرد، به عنوان مثال 0 یا 1. این شیوه کدگذاری باید برای همه بلوکها (تیمارها) یکسان در نظر گرفته شود.
آزمونهای مرتبط
روشهای ناپارامتری «آزمون فریدمن» (Friedman Test) یا «آزمون دوربین-واتسون» (Durbin-watson Test) را میتوان زمانی استفاده کرد که متغیر پاسخ مقادیر دو دویی نداشته و شامل دادههای ترتیبی یا کمی باشند. در ضمن اگر دقیقاً دو تیمار یا گروه وجود داشته باشد، آزمون کوکران Q معادل «آزمون مکنمار» (McNemar Test) خواهد بود که مشابه «آزمون علامت دو طرفه» (Two-tailed sign test) است.
آزمون کوکران Q در SPSS
آزمون SPSS Cochran Q روشی برای اجرای آزمون آماری است که برای بررسی یکسان بودن نسبت 3 متغیر یا بیشتر در جمعیت به کار میآید. این متغیرهای پاسخ، بر روی همان افراد یا سایر واحدهای آماری اندازهگیری شدهاند. در نتیجه یک طرح با مقادیر تکراری داریم. برای روشن شدن نحوه اجرای این آزمون از نرمافزار SPSS استفاده کردهایم و براساس یک فایل داده، مثال را دنبال خواهیم کرد.
مثال آزمون کوکران Q برای دشواری امتحان پذیرش دانشجو در SPSS
مدیر دانشگاهی میخواهد بداند که سه آزمون اجرا شده برای جذب دانشجو در رشته آمار، به یک اندازه دشوار بودهاند یا خیر. پانزده دانشجو در این سه نوع آزمون شرکت کردهند و نتایج آنها در فایل اطلاعاتی examn_results.sav ثبت شده است. این فایل را میتوانید با قالب فشرده از اینجا دریافت کنید و پس از خارج کردن از حالت فشرده در نرمافزار SPSS بارگذاری نمایید.
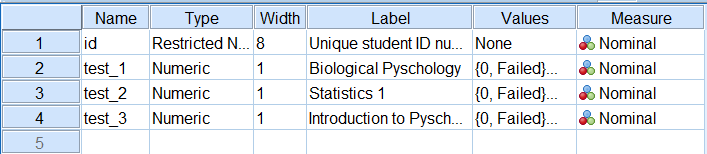
ابتدا نگاهی به این مجموعه داده میاندازیم. در تصویر ۱، نمای دادهها (Data View) و در تصویر ۲ نیز نمای متغیرها (Variable View) دیده میشود. مشخص است که گزینه Failed نشانگر مردود شدن در آزمون (با کد ۰) و قبولی نیز با با کد ۱ در این مجموعه داده قرار گرفته است. به این ترتیب سازگاری در داوری توسط این سه آزمون برای دانشجویان توسط آزمون کوکران Q مورد بررسی و ارزیابی قرار میگیرد.
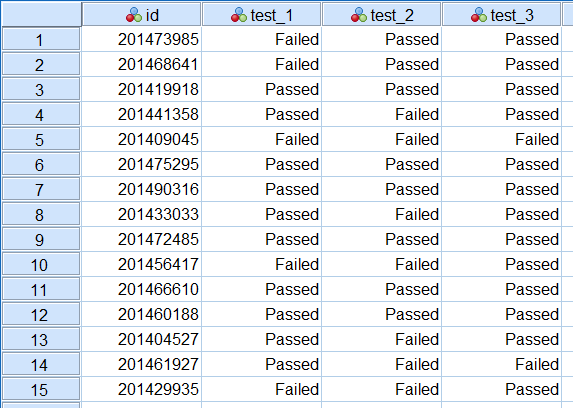
واضح است که سطوح مقادیر متغیرها ۰ و ۱ بوده و متغیرها نیز تیمارها را مشخص کردهاند. در اینجا هر سطر نشانگر یک بلوک است. در ادامه بعضی از بررسیهای توصیفی در مورد این مجموعه داده را اجرا کرده، سپس به آزمون آماری کوکران Q خواهیم پرداخت.
بررسی سریع داده ها
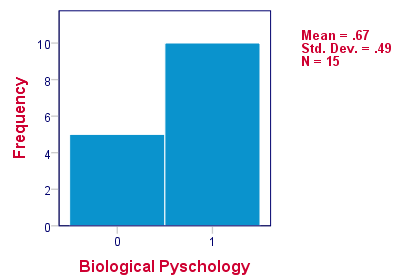
همیشه بهتر است قبل از انجام هرگونه تست آماری، نگاهی سریع به شکل ظاهری یا توزیع دادهها بیندازید. با اجرای دستور FREQUENCIES با نحو زیر، فایل دادهها را باز کرده و نمودار فراوانی یا «هیستوگرام» (Histogram) برای متغیرها را بازرسی میکنیم. این کار را در سه مرحله یا بخش توسط کد زیر اجرا کردهایم. توجه داشته باشید که این دستورات را باید در پنجره Syntax از نرمافزار SPSS کپی و اجرا کنید.
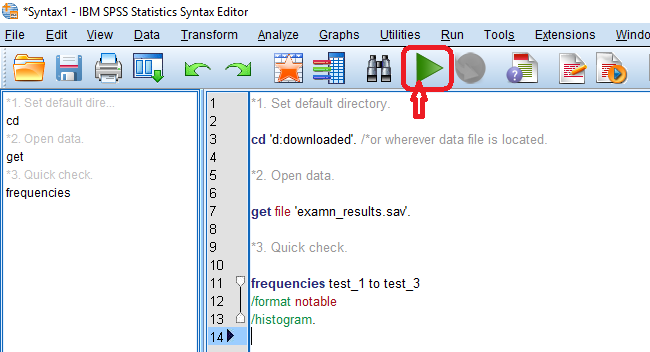
ابتدا پوشه فعال را با استفاده از دستور cd به درایو D و پوشه download تبدیل کردهایم و با دستور get file، فایل اطلاعاتی را فراخوانی کردهایم. فرض بر این است که فایل مورد نظر در این پوشه قرار دارد. در انتها هم، دستور frequencies برای رسم نمودار فراوانی به کار رفته است.
1*1. Set default directory.
2
3cd 'd:downloaded'. /*or wherever data file is located.
4
5*2. Open data.
6
7get file 'examn_results.sav'.
8
9*3. Quick check.
10
11frequencies test_1 to test_3
12/format notable
13/histogram.به کلید واژه to در مرحله 3 توجه کنید. عبارت frequencies test_1 to test_3 نشانگر آن است که از تیمار اول تا سوم برای رسم نمودار فراوانی به کار رفتهاند. به این ترتیب دیگر احتیاجی به نامبردن تک تک متغیرها نیست.
اجرای آزمون کوکران Q در SPSS
به منظور دسترسی به این آزمون لازم است از فهرست Analyze گزینه Nonparametric Tests را انتخاب و گزینه Legacy Dialogs را فعال کنید. انتخاب دستور K Related Samples شما را به پنجره این آزمون هدایت خواهد کرد.
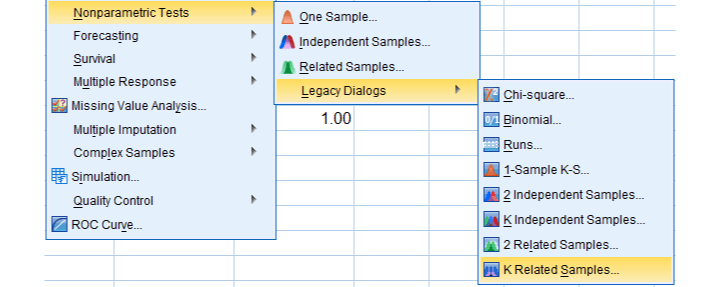
به این ترتیب، پنجرهای به نام Tests for Several Related Samples و به صورت زیر ظاهر شده تا پارامترهای مربوط به آزمون کوکران Q را از شما دریافت کند. واضح است که چون طرح به صورت بلوک است، هر نفر در بیش از یک تیمار اندازهگیری شده است. بنابراین مقادیر مرتبط (Related) هستند.
در تصویر 6، نمونهای از این پنجره را میبینید که برای حل این مثال تنظیم شده است. کافی است متغیرهای test_1, test_2 و test_3 را به کادر Test Variables ببرید و گزینه Cochran's Q را فعال کنید. برای مشاهده شاخصهای آماری نیز از دکمه Statistics کمک بگیرید.
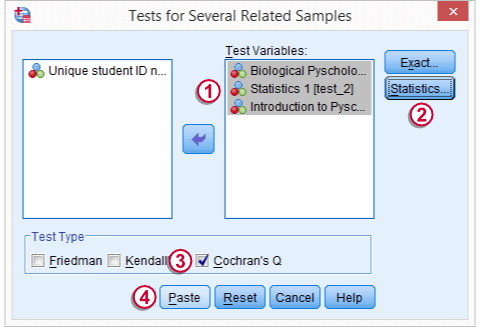
برای استفاده از توزیع دقیق آماره آزمون نیز از دکمه Exact کمک بگیرید.
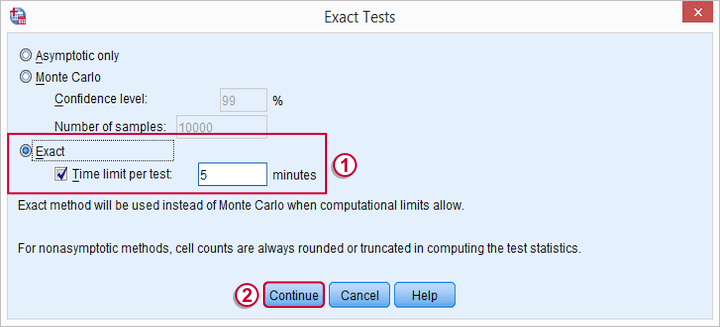
اگر به جای فشردن دکمه OK، از دکمه Paste استفاده کنید، کد مربوط به اجرای این آزمون براساس پارامترهای تنظیم شده در پنجره Syntax ظاهر خواهد شد. این کد را در ادامه مشاهده میکنید.
1*Run Cochran Q test.
2
3NPAR TESTS
4/COCHRAN=test_1 test_2 test_3
5/STATISTICS DESCRIPTIVES
6/MISSING LISTWISE.نکته: آزمونهای مشابه نظیر «آزمون فریدمن» (Friedman Test) و «آزمون کندال» (Kendall's W) نیز در این پنجره قابل انتخاب هستند ولی توجه داشته باشید که از این آزمونها برای دادههای دودویی نباید استفاده کرد.
خروجی و تفسیر آزمون کوکران Q
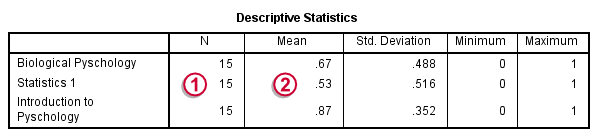
اولین جدول خروجی به نام Descriptive Statistics ظاهر میشود. در این جدول ستونهایی N و Mean (که با شماره ۱ و ۲ در تصویر 8، مشخص شدهاند) اهمیت دارند. از آنجایی که N=15 است، هیچ مشاهدهای شامل «مقدار گمشده» (Missing) نیست.
از طرفی میانگین یا همان درصد مقادیر ۱، برای هر سه نوع تیمار در ستون Mean دیده میشود که از ۰٫۵۳ تا ۰٫۸۷ تغییر میکنند. میخواهیم بدانیم که این تفاوتها، تصادفی است یا از لحاظ آماری معنیدار است. از آنجایی که دادهها، باینری هستند، میانگین به معنی درصد بوده و «واریانس» (Variance) یا «انحراف معیار» (Std. Deviation) معنی خاصی نخواهند داشت. مشخص است که «حداقل» (Minimum) و «حداکثر» (Maximum) مقادیر نیز به ترتیب ۰ و ۱ هستند.
در جدول بعدی که Test Statistics نام دارد، «آماره آزمون» (Cochran's Q) و «درجه آزادی» (df) به همراه «مقدار احتمال مجانبی» (Asymp. Sig) دیده میشود. با توجه به سطح آزمون ۰٫۰۵ و مقایسه با مقدار احتمال مجانبی (شماره ۱ در تصویر 9) فرض صفر رد نمیشود.
Asymp. Sig. = 0.093 > 0.05
میتوان نتیجه گرفت که این سه تیمار در سطح خطای ۰٫۰۵، یکی بوده و این نمونه دلیلی برای رد فرض صفر (برابری درصد تیمارها) ارائه نمیکند.

توجه داشته باشید که مقدار آماره Q، دقیق محاسبه شده است ولی توزیع آن به صورت مجانبی حاصل شده که همان توزیع کای ۲ است. معمولا در گزارشات و تحقیقات آماری این نتیجه را در یک جمله به مانند عبارت زیر خلاصه میکنند.
آزمون کوکران Q، نتوانست اختلاف معنیداری در نسبت سه تیمار مشخص کند، .
خلاصه و جمعبندی
آزمون کوکران Q برای زمانی که با دادههای دو وضعیتی (مثل ۰ و ۱) مواجه هستیم و میخواهیم بیش از ۳ تیمار را مورد بررسی و آزمون آماری قرار دهیم، به کار میآید. از آنجایی که این آزمون ناپارامتری است، به توزیع دادهها کمتر توجه شده و براساس فراوانیها (تعداد مقادیر ۱) در هر تیمار، محاسبات آماره آزمون صورت گرفته و ناحیه بحرانی تعیین میگردد. در این متن، به منظور اجرای چنین آزمونی از نرمافزار محاسبات آماری SPSS استفاده کرده و بر طبق یک مثال کاربردی با دادههای واقعی، نحوه اجرای این آزمون را در SPSS فرا گرفتیم.












