متغیر دو وضعیتی (Dichotomous) در SPSS — راهنمای کاربردی

بیشتر اطلاعاتی که در تحلیل داده‌ها به کار گرفته می‌شوند باید در قالب اعداد ثبت و پردازش شوند. به این ترتیب داده‌های کمی با توجه به ماهیت عددی، بیشتر در تحلیل‌های آماری به کار می‌روند. ولی از طرفی برای داده‌های کیفی نیز روش‌های خاصی به منظور استنباط آماری وجود دارد. اما برای ورود این متغیرها به نرم‌افزارهای محاسبات و تحلیل آماری از تبدیل‌هایی استفاده می‌شود که به کمک آن‌ها می‌توان مقادیر متنی را به صورت عددی نمایش داد. در این نوشتار به بررسی متغیرهای «دو وضعیتی» (Dichotomous) پرداخته و شیوه کار با آن‌ها را در نرم‌افزار SPSS فرا می‌گیریم.

در دیگر نوشته‌های فرادرس مانند جامعه آماری — انواع داده و مقیاس‌های آن‌ها با انواع مقیاس‌ها و نوع داده آشنا شده‌اید. در این مطلب سعی داریم که کار با داده و اطلاعاتی که به صورت دو وضعیتی هستند را فرا گرفته و با شیوه شناسایی، کاربردهای آماری آن ها بیشتر آشنا شویم. به منظور آگاهی از مفاهیم مربوط به آزمون‌های آماری بهتر است مطلب را مطالعه کنید. همچنین خواندن مطلب رگرسیون خطی با متغیرهای طبقه‌ ای در SPSS — راهنمای گام‌ به‌ گام و رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS که در مورد استفاده از داده‌های دو وضعیتی در ایجاد مدل‌های رگرسیونی است، نیز خالی از لطف نیست.

متغیر دو وضعیتی

اگر یک ویژگی یا صفت بطوری باشد که مقدار آن برای هر یک از مشاهدات مربوط به نمونه‌های تصادفی، براساس وجود یا ناموجود بودن آن ویژگی، قابل اندازه‌گیری باشد، به آن متغیر دو وضعیتی گفته می‌شود.

فیلم آموزش مدل سازی معادلات ساختاری با نرم افزار آموس AMOS در فرادرس

کلیک کنید

برای ثبت چنین ویژگی‌هایی در نرم‌افزارهای آماری از متغیرهای «دو وضعیتی» (Dichotomous) استفاده می‌شود. اگر به تصویر زیر دقت کنید متغیرهای «جنسیت» و q1 از نوع کیفی و به صورت متغیر دو وضعیتی ثبت شده‌اند.

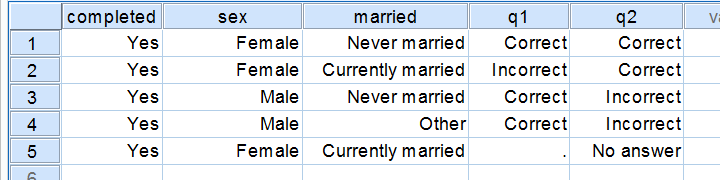
با توجه به تصویر بالا، می‌توانیم متغیرهای دوتایی یا دو وضعیتی را مطابق فهرست زیر شناسایی کنیم.

• در ستون اول completed متغیر دو وضعیتی نیست. زیرا به نظر می‌رسد که همیشه دارای مقدار ثابت Yes است.
• در ستون دوم «جنسیت» یک متغیر دو وضعیتی است. زیرا حالت‌های مختلف آن فقط دو مقدار Female و Male است.
• ستون سوم یا متغیر married یا متغیر «وضعیت تاهل» ممکن بود که به صورت دو وضعیتی در آید ولی وجود مقدار Other باعث شده که سه نوع مقدار برای چنین متغیری در نظر گرفته شود.
• ستون چهارم یعنی q1 متغیر دو وضعیتی است که دو مقدار Correct و Incorrect برایش در نظر گرفته شده است. هر چند یک مقدار گمشده (Missing Value) در این ستون قرار گرفته است ولی چون مقادیر گمشده در محاسبات و تحلیل‌ها به کار گرفته نمی‌شوند، متغیر q1 دو وضعیتی خواهد بود.
• ستون پنجم نیز که با نام q2 مشخص شده است، متغیر دو وضعیتی نیست زیرا برای مقدارهای مختلف آن سه حالت متفاوت Correct، Incorrect و البته No answer منظور شده است. البته اگر No answer را به عنوان مقدار گمشده در نظر بگیریم می‌توان متغیر q2 را هم به صورت دو وضعیتی در نظر گرفت.

اهمیت استفاده از داده‌ها یا متغیرهای دو وضعیتی

یکی از ویژگی‌های مهم در متغیرهای دو وضعیتی در تحلیل‌های آماری، آگاهی از اندازه نمونه و جدول فراوانی است. به این ترتیب اگر بدانیم که در بین نمونه تصادفی با اندازه ۱۰۰، مردان ۴۵٪ از نمونه را تشکیل می‌دهند، همه اطلاعات در مورد توزیع جمعیت را می‌دانیم. به این معنی که مشخص است ۴۵ نفر از افراد نمونه مرد و ۵۵ نفر نیز زن هستند. بر این اساس رسم یک نمودار فراوانی به خوبی این توزیع را نشان می‌دهد.

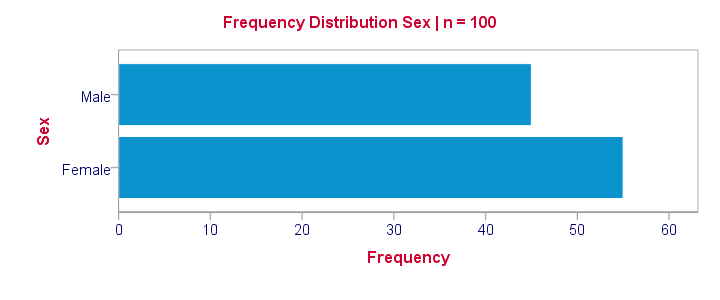
باید توجه داشت که این وضعیت برای «متغیر طبقه‌ای» (Categorical Variable) وجود ندارد. برای مثال اگر بدانیم که ۴۵٪ یک نمونه ۱۰۰ تایی از دانشجویان، ترم یک هستند، نمی‌توانیم اطلاعاتی در مورد تعداد دانشجویان ترم‌های دیگر کسب کنیم. تنها اطلاعاتی که از عبارت بالا درک خواهیم کرد این است که ۵۵٪ دانشجویان ترم یک نیستند. به این ترتیب ترم تحصیلی دانشجویان را به یک متغیر دو وضعیتی تبدیل کرده‌ایم که بیانگر حضور دانشجو در ترم یک یا غیر از آن است. در ادامه متوجه خواهیم شد که این کار باعث ایجاد متغیر دو وضعیتی مصنوعی شده است.

متغیر دو وضعیتی و متغیرهای طبقه‌ای و کمی

برای انجام تجزیه و تحلیل آماری باید نوع داده از قبل مشخص باشد تا بتوان بهترین روش یا تکنیک را برای بررسی چنین داده‌هایی به کار برد. داده‌ها و مقیاس‌های آن‌ها، معمولا به دو گروه تقسیم می‌شود. گروه اول «داده‌های طبقه‌ای» (Categorical) و گروه دوم «داده‌های کمی» (Metric) نامیده می‌شوند. داده‌های طبقه‌ای نیز ممکن است به صورت «اسمی» (Nominal) یا «ترتیبی» (Ordinal) باشند. همچنین داده‌های کمی نیز به دو دسته «فاصله‌ای» (Interval) و «نسبی» (Ratio) تقسیم می‌شوند. ولی داده‌های دو وضعیتی به علت ماهیتی که دارند در هر دو گروه قرار می‌گیرند. این وضعیت به چنین متغیرهایی امکان تفکیک جامعه یا گروهی از مشاهدات را به دو دسته جدا از هم می‌دهد.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

متغیر دو وضعیتی در تحلیل‌های آماری

هر چند ماهیت متغیرهای دو وضعیتی مشخص است ولی نقش آن‌ها در تحلیل‌های آماری بخصوص هنگام انجام آزمون‌ها آماری متفاوت است. در ادامه به بررسی کارکردهای این نوع متغیرها در حل مسائل تحلیل داده و آزمون فرض آماری خواهیم پرداخت.

آزمون فرض آماری برای نسبت

در بعضی از پرسشنامه‌ها یا تحقیق‌های میدانی، به وضعیتی بر می خوریم که ویژگی قابل اندازه‌گیری برای هر مشاهده فقط یکی از دو مقدار تعیین شده است. برای مثال ممکن است از هر نفر پرسیده شود که در یک سال گذشته آیا به سفر رفته‌اند یا خیر. این وضعیت در تصویر زیر دیده می‌شود. همانطور که مشخص است، برای سنجش درصد کسانی که در سال گذشته به سفر رفته‌اند بطور مستقیم از متغیر consider که تعیین کننده نوع پاسخ است، استفاده می‌شود. روش‌های تحلیل آماری و آزمون‌ها مرتبط در چنین حالتی، می‌توانند «آزمون‌ دوجمله‌ای» (Binomial test) یا «آزمون Z برای نسبت» (Z-test for one proportion) باشند.

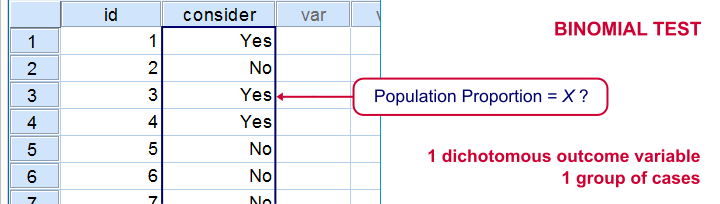
همانطور که در تصویر بالا می‌بینید در آزمون دوجمله‌ای، هدف پیدا کردن نسبت افرادی است که به مسافرت رفته‌اند. در نتیجه به نظر می‌رسد که در این حالت علت استفاده از متغیر دو وضعیتی، شناسایی و انجام آزمون برای نسبت یا درصد یک گروه از مشاهدات (groups of cases) باشد.

آزمون فرض آماری برای دو گروه مستقل

ولی از طرفی ممکن است که به کمک متغیر دو وضعیتی، جامعه را به دو گروه مستقل تفکیک کنیم. در این وضعیت، هدف از انجام آزمون آماری ممکن است مقایسه میانگین بین دو گروهی باشد که توسط متغیر دو وضعیتی ایجاد شده است. تصویر زیر چنین حالتی را نشان می‌دهد.

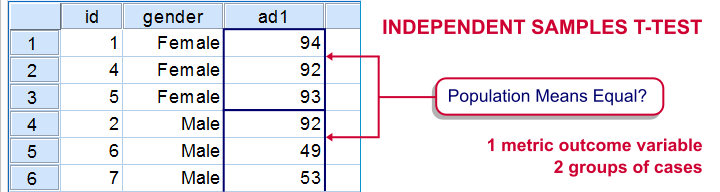
همانطور که می‌بینید، می‌توانیم بوسیله آزمون‌های مقایسه میانگین در دو جامعه مستقل (Independent Sample T-Test) در SPSS، تشخیص دهیم آیا در بین دو گروه زن و مرد که توسط متغیر gender‌ مشخص شده‌اند، میانگین متغیر ad1 تفاوت معنی‌داری ایجاد می‌کند یا خیر. به بیان دیگر، می‌توانیم آزمون کنیم که آیا جنسیت در مقدار متغیر ad1 تغییر ایجاد می‌کند. مشخص است که متغیر دو وضعیتی در اینجا به طور مستقیم در تحلیل حضور ندارد بلکه دو گروه‌‌‌ ایجاد شده توسط آن، برای مقایسه مشاهدات به کار می‌روند.

رگرسیون خطی و متغیرهای مجازی

فرض کنید قرار است یک مدل رگرسیونی را بین متغیرهای مستقل و وابسته ایجاد کنید. ممکن است در بین متغیرهای مستقل، یک یا چند متغیر طبقه‌ای نیز وجود داشته باشد. در چنین حالتی، استفاده از متغیر طبقه‌ای ممکن است الگوی مدل رگرسیونی را دچار اشتباه کند. برای مثال فرض کنید که مدل رگرسیونی با متغیر طبقه‌ای $$X$$ با سه سطح (کم، متوسط، زیاد) به صورت زیر در آمده است.

$$\large y = b_0+b_1x$$

در این صورت اگر مقدار «کم» را با عدد صفر و مقدار «متوسط» را با عدد ۱ و در انتها مقدار «زیاد» را با عدد ۲ بیان کنیم به نظر می‌رسد که اگر $$b_0=0$$ باشد، مقدار پیش‌بینی شده برای متغیر $$y$$ در سطح «زیاد» همیشه دو برابر مقدار پیش‌بینی شده برای سطح «متوسط» باشد که به نظر صحیح نمی‌رسد. راه حل عبور از این تبدیل متغیرهای طبقه‌ای به «متغیرهای مجازی» (Dummy Variable) هنگام ایجاد مدل رگرسیونی است. به این ترتیب یک متغیر طبقه‌ای با $$n$$ سطح یا مقدار مختلف تبدیل به $$n$$‌ متغیر مجازی یا دو وضعیتی می‌شود تا در تحلیل رگرسیونی به کار رود. تصویر زیر چنین وضعیتی را نشان داده است. نوع «حیوان خانگی» (pet) از هر یک از افراد پرسیده شده است. با توجه به کد 1 تا 4 برای حیوانات خانگی، استفاه از متغیر مجازی در مدل‌بندی رگرسیونی در چنین حالتی ضروری است. همانطور که می‌بینید متغیرهای مجازی ایجاد شده در ستون‌های pet_d1 تا pet_d4 دارای دو مقدار یا وضعیت 0 یا 1هستند.

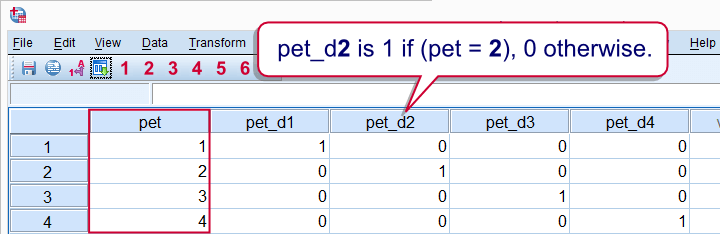
ایجاد متغیرهای دو وضعیتی در SPSS

باید توجه داشت که متغیرهای دو وضعیتی در SPSS، ممکن است به دو شکل ایجاد شوند. البته ذکر این نکته نیز ضروری است که نقشی که این دو نوع در انجام تحلیل‌های آماری دارند، نیز متفاوت خواهد بود.

• با توجه به ماهیت واقعی متغیر یا ویژگی که به صورت موجود یا ناموجود بودن یک خصیصه در مشاهده مورد نظر تعیین شده.
• براساس نیاز برای تفکیک مشاهدات به دو گروه مختلف با استفاده از تبدیلاتی روی متغیرهای دیگر

در حالت اول متغیر دو وضعیتی را «طبیعی» (Natural Dichotomous) نامیده ولی در حالت دوم آن را «غیرطبیعی» یا «مصنوعی» (Unnatural Dichotomous) نام‌گذاری کرده‌اند.

ایجاد متغیرهای دو وضعیتی طبیعی

به منظور ایجاد متغیرهای دو وضعیتی طبیعی در SPSS‌ کافی است که در برگه Variable View در پنجره Data Editor ویژگی‌های متغیر مورد نظرتان را وارد کنید و فقط در قسمت Value Label سطوح متغیر دو وضعیتی را برای حالت 0 و 1 تعیین و نام‌گذاری کنید. برای مثال اگر قرار است متغیری با نام Confirm ایجاد کنید که دارای دو مقدار Yes و No است، مطابق با تصویر زیر عمل کنید.

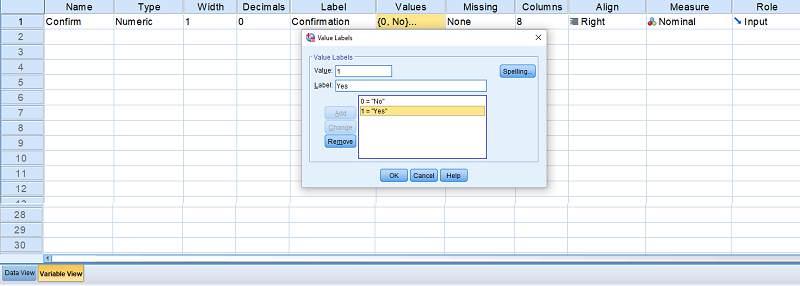
اگر پس از ایجاد این متغیر در برگه Data View‌ به جای نمایش برچسب فقط مقدارهای 0 و 1 نمایش داده می‌شود کافی است با فشردن دکمه‌ای از نوار ابزار که در تصویر زیر دیده می‌شود، نمایش برچسب‌های مقدارها (Value Label) را فعال کنید.

ایجاد متغیرهای دو وضعیتی مصنوعی

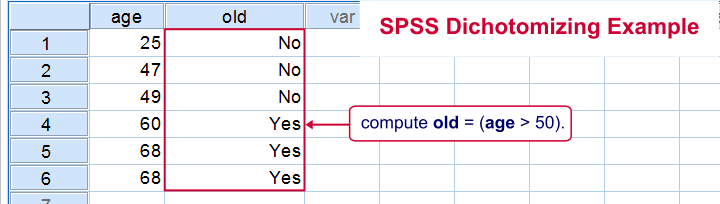
فرض کنید متغیری به نام «سن» (age) در مجموعه داده قرار دارد. می‌خواهید براساس این متغیر، جامعه را به دو گروه مجزا تفکیک کنید. قاعده یا قانون برای این کار نیز به این صورت است که افراد با سن کمتر از ۱۸ در گروه ۱ قرار گرفته و افرادی که بیش از 19 سال سن دارند در گروه ۲ دسته‌بندی شوند. ممکن است بعدها بخواهیم براساس متغیر جدید ساخته شده دست به انجام آزمون‌های آماری بزنیم.

فیلم آموزش تحلیل های رگرسیونی با اس پی اس اس SPSS در فرادرس

کلیک کنید

برای انجام این کار در SPSS روش‌های مختلف وجود دارد. یکی از این روش‌ها، ایجاد متغیر جدید به کمک دستور ...Recode into Different variables از فهرست Transform است. تصویر زیر این امر را به خوبی نشان داده است.

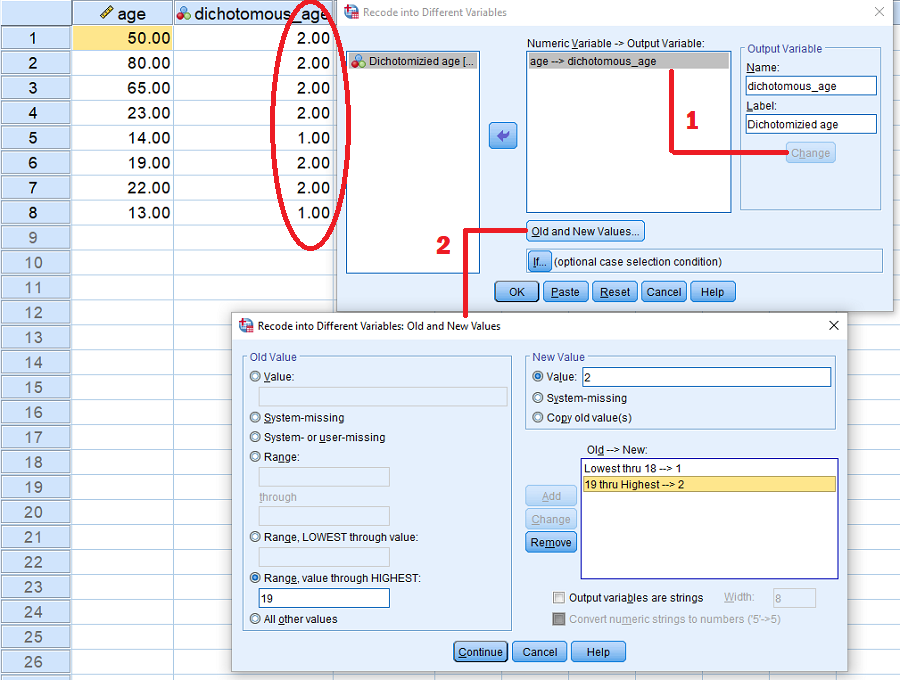
دقت کنید که متغیر جدید با نام dichotomous_age با دو سطح یا مقدار 1 و 2 ایجاد شده است. مقادیر مربوط به این تبدیل در ستون مربوطه قابل مشاهده است.

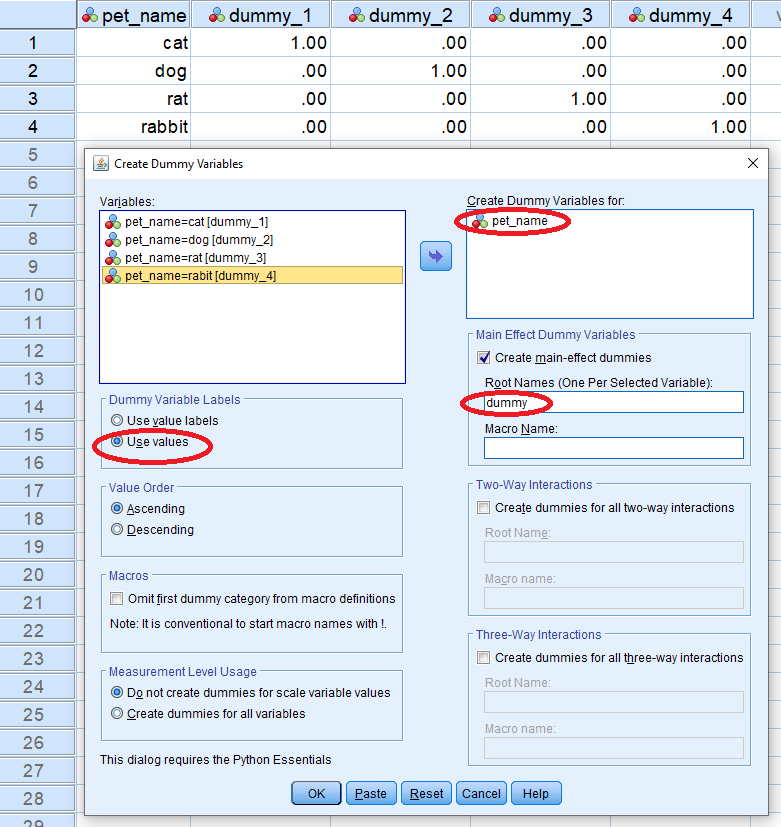
روش دیگر برای ایجاد متغیرهای دو وضعیتی از روی متغیرهای طبقه‌ای، استفاده از دستور Create Dummies از فهرست Transform است. انجام چنین کاری وابسته به وجود افزونه Python در SPSS است. در تصویر زیر مشاهده می‌کنید که متغیر pet_name با مقادیر عددی 1 تا 4 با توجه به برچسب‌های cat, dog, rat, rabbit تبدیل به متغیرهای مجازی با مقدارهای 0 و 1 شده است. واضح است که تعداد متغیرهای مجازی برابر با تعداد سطوح متغیر طبقه‌ای است.

خلاصه

مشخص است که از متغیرهای دو وضعیتی برای دسته‌بندی یا گروه‌بندی جامعه یا نمونه آماری می‌توان استفاده کرد. برای مثال می‌توانید به کمک این روش، میانگین درآمد افراد را در بین دو طبقه سنی ایجاد شده مقایسه کنید. از طرفی رسم نمودارهایی نیز به کمک چنین متغیرهایی برای درک و مقایسه بهتر مقادیر متغیرهای کمی بین دو گروه یا دو جامعه مناسب است. همانطور که گفته شد ایجاد متغیرهای مجازی که به از نوع متغیرهای دو وضعیتی هستند، هنگام استفاده از متغیرهای طبقه‌ای در مدل‌سازی به کمک رگرسیون خطی لازم است تا مدل ساخته شده، به درستی مقادیر را پیش‌بینی یا پیش‌گویی کند.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های SPSS
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش همبستگی و رگرسیون خطی در SPSS
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• رگرسیون خطی با متغیرهای طبقه‌ ای در SPSS — راهنمای گام‌ به‌ گام
• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی

^^