آزمون دوربین واتسون (Durbin–Watson Test) – به زبان ساده

در آمار، یکی از روشهای تشخیص وابستگی بین باقیماندهها، مثلا در یک مدل رگرسیونی (Ordinary Linear Regression) یا سری زمانی (Time Series)، استفاده از آزمون دوربین واتسون (Durbin-Watson) است. با این تکنیک همچنین میتوانیم وابستگی بین مشاهدات سری زمانی با تاخیر یک واحد را مشخص کنیم. این آزمون به افتخار «جیمز دوربین» (James Durbin) آمارشناس انگلیسی و «جوفری واتسون» (Geoffery Watson) دانشمند استرالیایی آمار که در سالهای 1950-1951 روی این موضوع کار کردند، آزمون دوربین واتسون نامیده میشود. البته در سال 1941 «جان فون نومن» (John von Neumann) گونهای از این آزمون را برای اندازه نمونههای کوچک ابداع کرده بود.
خودهمبستگی (Autocorrelation) و یا اصطلاح همبستگی سریالی (Serial Correlation) زمانی به کار میرود که مقادیر یک متغیر با یکدیگر وابستگی داشته باشند. به این ترتیب مشخص است که از آزمون دوربین واتسون بخصوص در مدلهای رگرسیون و تحلیل استقلال بین باقیماندههای مدل باید استفاده شود. برای آشنایی بیشتر با آزمون فرض آماری به نوشتار استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات مراجعه کنید. همچنین اگر لازم است در مورد تحلیل رگرسیونی، اطلاعاتی به عنوان مقدمه این بحث داشته باشید، خواندن مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده توصیه میشود. علاوه بر این موارد خواندن آزمون نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای۲ نیز خالی از لطف نیست.


آزمون دوربین واتسون
آزمون دوربین واتسون یا به اختصار (DW)، روشی برای تشخیص همبستگی در باقیماندههای تحلیل مدل رگرسیونی است. همچنین در زمانی که از تحلیل سری زمانی با مدل خودهمبستگی (Autoregresive) استفاده میکنید، باید باقیماندههای مدل با تاخیر واحد یا مدل مستقل از یکدیگر باشند. این امر را میتوان بوسیله آزمون دوربین واتسون هم، مورد بررسی قرار داد.
در صورتی که در یک مدل، خودهمبستگی وجود داشته باشد، برآورد واریانس و انحراف استاندارد دچار مشکل شده و ممکن است پارامترهای مدل به درستی برآورد نشوند. به این ترتیب استفاده از آزمون دوربین واتسون موثر بوده و نتایج تحلیلها را قابل اعتماد میکند.
پیشفرضهای به کارگیری آزمون دوربین واتسون به صورت زیر هستند:
- فرض صفر (Null Hypothesis) در این جا عدم خودهمبستگی مرتبه اول است. به این معنی که برای دادهها (باقیماندهها) همبستگی بین باقیمانده در زمان و وجود ندارد یا صفر است که آن را بر حسب تابع خودهمبستگی (Autocorrelation Function) یا ACF به صورت نشان میدهیم.
- فرض مقابل در آزمون دوربین واتسون، وجود همبستگی سریالی بین مشاهدات یا باقیماندههای تاخیر واحد است. به این معنی که همبستگی بین باقیماندههای زمان و مخالف صفر است. البته این وابستگی را با مشخص میکنیم.
- دادهها (باقیماندههای مدل) دارای توزیع نرمال هستند. بررسی صحت این فرض را میتوان بوسیله آزمونهای نرمال بودن (Normality Test) نظیر آزمون کولموگروف اسمیرنف (Kolmogorov-Smirnov) یا آزمون شاپیرو ویلک (Shapiro-Wilk's Test) انجام داد. در صورتی که باقیماندهها دارای توزیع نرمال نباشند، امکان استفاده از آزمون دوربین واتسون وجود ندارد.
- دادهها (باقیماندههای مدل) ایستا (Stationary) هستند. به این معنی که با تغییر زمان میانگین تغییر نخواهد کرد و باقیماندهها در طول زمان دارای روند صعودی یا نزولی نیستند. این امر، یکی از شرطهای تحلیل سری زمانی نیز هست.
برای مثال فرض کنید که ارزش سهام یک شرکت خودهمبستگی مثبت را نشان دهد. این امر به این معنی است که ارزش سهام دیروز دارای همبستگی مثبت با ارزش سهام امروز دارد. بنابراین اگر ارزش سهام دیروز مشخص شده باشد، میتوانیم ارزش سهام امروز را حدس بزنیم و اگر دیروز ارزش سهام نزولی بوده امروز نیز نزولی خواهد بود. البته نمیتوان میزان نزولی بودن آن را دقیق مشخص کرد ولی با وجود خودهمبستگی مثبت بین ارزش سهام شرکت انتظار داریم که براساس اطلاعات گذشته، بتوانیم ارزش آتی سهام شرکت را حدس بزنیم.
نکته: این موضوع برای دادهها، یعنی وجود یک همبستگی بین دادههای زمانی، منجر به استفاده از تحلیل سری زمانی خواهد شد که البته برای ایجاد مدل مناسب است. ولی آنچه در آزمون خودهمبستگی در این بحث وجود دارد، شرط استقلال باقیماندهها است که در آزمون دوربین واتسون به کار میرود. در نتیجه مثال بالا فقط برای توضیح وجود خودهمبستگی به کار رفت ولی هدف از انجام آزمون دوربین واتسون روی باقیماندههای مدل است نه دادههای مربوط به متغیرهای مستقل یا وابسته.
به این ترتیب فرض صفر و مقابل برای آزمون دوربین واتسون را به صورت زیر نشان میدهیم.
آماره آزمون دوربین واتسون
فرض کنید باقیمانده مدل در زمان باشد، رابطه بین باقیماندهها نیز به صورت زیر در نظر گرفته شده است که بیانگر رابطه با تاخیر زمان واحد است.
اگر ضریب میزان خطا در زمان صفر باشد یعنی داشته باشیم آنگاه، میتوان وابستگی با تاخیر زمان واحد را صفر در نظر گرفت.
بنابراین فرض صفر به صورت نوشته شده و فرض مقابل نیز به شکل خواهد بود. پس فرض صفر و مقابل برای آزمون دوربین واتسون را به صورت زیر نیز میتوان نشان داد.
اگر آماره آزمون را به صورت زیر در نظر بگیریم، میتوانیم از آن برای بررسی فرض صفر در آزمون دوربین واتسون استفاده کنیم.
رابطه ۱
در رابطه ۱، مقدار ، همان تعداد مشاهدات است. صورت این کسر شبیه کوواریانس بوده و مخرج نیز به واریانس شباهت دارد. به این ترتیب میتوان آماره آزمون دوربین واتسون را مشابه ضریب همبستگی پیرسون (Pearson Correaltion) در نظر گرفت. اگر برآورد مقدار باشد، میتوان نتیجه گرفت که بین و رابطه زیر برقرار است.
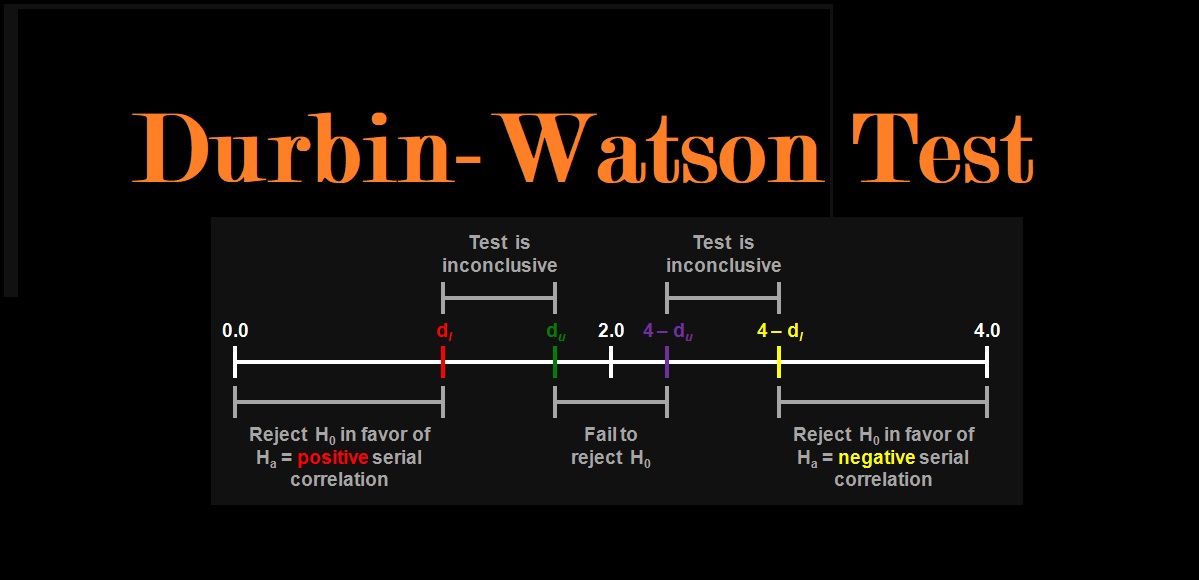
به این ترتیب صفر بودن مقدار نشانگر آن است که باید باشد. مقدار 2.0 برای به این معنی است که هیچ همبستگی در نمونه مشاهده نشده است. آماره Durbin-Watson یعنی ، همیشه یک مقدار بین 0 تا 4 خواهد داشت. مقادیر 0 تا کمتر از 2 بیانگر همبستگی مثبت است و مقادیر 2 تا 4 بیانگر همبستگی منفی است. به بیان دیگر اگر مقدار آماره آزمون کمتر از ۱ یا بیشتر از ۳ باشد، نشانگر خودهمبستگی مرتبه ۱ شدید در بین دادهها است. در مدلی با این وضعیت برآوردگرهای مدل، دچار کمبرآورد (Underestimate) شدهاند و خطای زیادی برای مدل کردن دادههای جدید رخ خواهد داد.
نواحی بحرانی برای آزمون دوربین واتسون
برای مقدارهای مثبت خودهمبستگی در سطح و نواحی بحرانی میتوان آزمون را به صورت زیر در نظر گرفت. توجه داشته باشید که منظور از مقدار پایینی برای ناحیه بحرانی آزمون دوربین واتسون است. همچنین نیز کران بالایی را نشان میدهد.
- اگر باشد فرض صفر را در سطح رد میکنیم.
- اگر باشد، در سطح شواهدی مبنی بر رد فرض صفر نداریم.
- اگر باشد فرض صفر را در سطح نه میتوان رد کرد و نه شواهدی مبنی بر تاییدی آن در اختیار داریم.
در اینجا منظور از خودهمبستگی یا همبستگی سریالی مثبت، آن است که جهت تغییرات خطاها یکسان است یعنی اگر یکی از باقیماندهها یا مقادیر خطا افزایش یابد، احتمال آنکه دیگری نیز افزایش داشته باشد، زیاد خواهد بود.
این آزمون برای خودهمبستگی منفی نیز در سطح خطای آزمون ، براساس نوشته خواهد شد. به این ترتیب خواهیم داشت:
- اگر باشد، آنگاه فرض صفر را رد میکنیم. در این صورت آزمون نشانگر وجود همبستگی منفی بین جملات خطا خواهد بود.
- اگر باشد، آنگاه شواهد یا دلیلی مبنی بر وجود خودهمبستگی منفی نخواهیم داشت و فرض صفر رد نمیشود.
- اگر باشد فرض صفر را در سطح نه میتوان رد کرد و نه شواهدی مبنی بر تاییدی آن در اختیار داریم.
همبستگی سریالی منفی، نشانگر آن است که اگر مقدار خطا در یک مشاهده افزایش داشته باشد، شانس کاهش برای مقدار خطای بعدی زیاد خواهد بود و برعکس اگر مقدار خطا کاهش داشته باشد، احتمال مشاهده افزایش در خطای بعدی نیز وجود دارد. به این ترتیب در خودهمبستگی منفی، رابطه به صورت معکوس بین خطای مشاهدات در جملات متوالی وجود دارد.
مقدار کرانهای بالایی و پایینی برای آماره دوربین واتسون وابسته به سطح آزمون () بوده و براساس آن تغییر میکند. در ادامه جدولی از این مقادیر را برای سطح آزمون مشاهده میکنید.
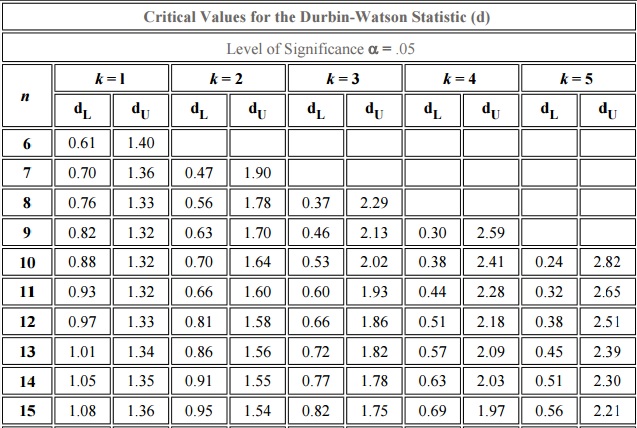
در این جدول نشانگر تعداد مشاهدات (Observations) و نیز تعداد متغیرهای مدل (Regressor) بدون در نظر گرفتن عرض از مبدا (مقدار ثابت) است. برای مثال اگر از مدلی استفاده میکنید که مقدار ثابت و فقط یک متغیر مستقل در آن وجود داشته باشد، برای تعداد مشاهدات برابر با ۱۰، کران بالا برای آماره دوربین واتسون 1٫32 و کران پایین نیز 0٫88 خواهد بود.
مثال 1
فرض کنید زوجهای مرتبی از مقادیر در اختیار داریم. مولفه اول این زوج مربوط به متغیر مستقل و مولفه دوم نیز متغیر وابسته را نشان میدهد. جدول اطلاعاتی به صورت زیر است.
| مشاهده | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ |
| مولفه اول () | 10 | 20 | 35 | 40 | 50 | 45 |
| مولفه دوم () | 1100 | 1200 | 985 | 750 | 1215 | 1000 |
جدول ۲: مقادیر متغیرهای وابسته و مستقل برای مدل رگرسیونی
مدل رگرسیونی خطی ساده (OLS) برای این دادهها به صورت زیر در خواهد آمد.
رابطه ۲
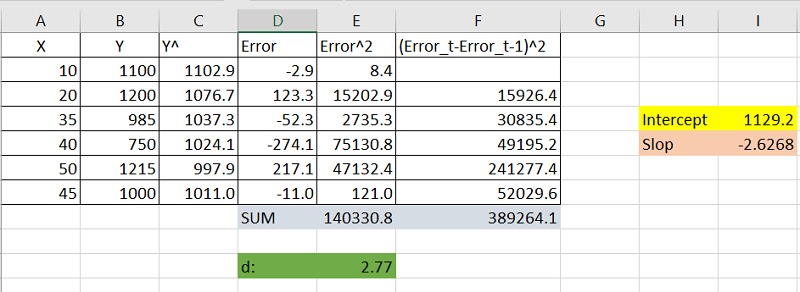
ارقام مربوط به رابطه ۲ را به وسیله اکسل محاسبه خواهیم کرد. واضح است که 1129.2 عرض از مبدا و 2.6268- شیب خط رگرسیونی است. تابع Intercept برای محاسبه عرض از مبدا و تابع Slope هم برای محاسبه شیب خط مناسب است.
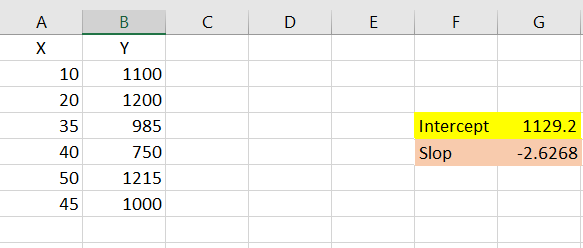
پارامترهای این توابع در تصویر زیر مشخص شدهاند.
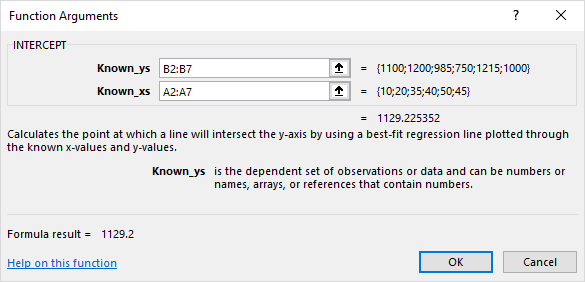
پارامتر اول نشانگر ستون یا بردار مقادیر متغیر وابسته است و پارامتر دوم نیز ناحیه مربوط به متغیر مستقل را مشخص میکند. با توجه به جدول یا کاربرگ ارائه شده، این نواحی باید برای پارامتر اول از سلول B2 تا B7 بوده و برای پارامتر دوم نیز ناحیه A2 تا A7 در نظر گرفته شود. پارامترهای تابع Slope نیز دقیقا به همین شکل است.
اولین گام برای محاسبه آماره آزمون دوربین واتسون، بدست آوردن خطا است که بوسیله برآورد مولفه دوم () برای مشاهدات حاصل میشود. جدول زیر مقادیر برآورده شده برای مولفه دوم توسط مدل رابطه ۲ را نشان میدهد.
| مشاهده | 1 | 2 | 3 | 4 | 5 | 6 |
| مولفه اول () | 10 | 20 | 35 | 40 | 50 | 45 |
| برآورد مولفه دوم () | 1102.9 | 1076.۷ | 1037.۳ | 1024.1 | 997.۹ | 1011 |
| خطا () | -2.9 | 123.3 | -52.۳ | -274.1 | 217.1 | -11 |
(جدول ۳: مقادیر پیشبینی شده و باقیماندهها (خطا
به این ترتیب براساس رابطه ۱ میتوان مقدار آماره دوربین واتسون را محاسبه کرد. کافی است که اختلاف خطای هر مشاهده را از مشاهده قبلی کم کنیم. این کار در جدولی که در ادامه قابل مشاهده است صورت گرفته است.
| مشاهده | 1 | 2 | 3 | 4 | 5 | 6 |
| اختلاف با تاخیر واحد | - | 123.3-(-2.9)=126.2 | -52.3-123.3=-175.6 | -274.1-(-52.33)=221.8 | 217.1-(-274.1)=491.2 | -11-217.1=-228.1 |
جدول ۴: اختلاف باقیماندهها (خطا) با تاخیر واحد (Lag=1)
مجموع مربعات مقادیر جدول ۴ را اگر بر مجموع مربعات سطر آخر جدول ۳ تقسیم کنیم، آماره دوربین واتسون بدست خواهد آمد. یعنی خواهیم داشت:
در تصویر زیر محاسبات صورت گرفته در اکسل را مشاهده میکنید.
حال با توجه به مقادیر بحرانی در سطح آزمون و با در نظر گرفتن و (مدل به صورت یک مقدار ثابت و شیب خط نوشته شده است)، کران بالا و پایین به صورت زیر خواهند بود.
در نتیجه با توجه به قواعدی که برای استنباط براساس کرانهای آماره دوربین واتسون ارائه کردیم، خواهیم داشت:
پس نمونه تصادفی، شاهدی بر داشتن خودهمبستگی مثبت (Positive Autocorrelation) بین باقیماندهها ارائه نکرده است. پس دلیلی بر رد صفر توسط این نمونه تصادفی وجود ندارد.
از طرفی برای همبستگی منفی نیز داریم:
پس از این آزمون برای سنجش همبستگی منفی (Negative Autocorrelation) در سطح خطای ۵٪ نمیتوان استفاده کرد.
البته در تصویر زیر محاسبات صورت گرفته توسط اکسل نیز دیده میشود. میتوانید فایل اطلاعاتی مربوط به این محاسبات را نیز از اینجا دریافت کنید.
کاربردهای آزمون دوربین واتسون
یکی از کاربردهای آزمون دوربین واتسون، بررسی داده پانلی به منظور به کارگیری مدل اثرات ثابت است.
تحلیل داده پانلی (Panel Data)
آماره آزمون دوربین واتسون برای استفاده در داده پانلی توسط «الوک بهارگوا» (Alok Bhargava) به صورت زیر در آمده است.
رابطه 3
در این جا فرض شده است که باقیمانده مدل رگرسیونی با اثرات ثابت (Fixed Effect) برای واحد ام هر مشاهده است به این معنی که در زمان مشاهده پنل دارای باقیمانده در مدل به صورت است.
برای بررسی نقاط بحرانی این آزمون نیز نیاز به جدولهای آماری از توزیع داریم که به ازای مقادیر مختلف و و البته تعداد متغیرهای پیشگو (Regressor) تهیه شدهاند. این جدولها برحسب خطای نوع اول جداگانه ارائه شده و به کار میروند.

آزمون خودهمبستگی برای مدل ARMA
متاسفانه آماره دوربین واتسون که در رابطه ۱ ارائه شد برای مدلهای میانگین متحرک خودهمبسته (Autoresgressive-Moving Average) یا ARMA مناسب نیست و دارای ارایبی (Basie) است.
برای نمونههای بزرگ میتوان از آماره استفاده کرد که با توجه به بزرگ بودن مقدار (تعداد مشاهدات) دارای توزیع نرمال است.
که در آن برآورد واریانس برآوردگرهای مدل رگرسیونی با تاخیر زمانی واحد است. البته این نکته نیز ضروری است که باید شرط زیر برای چنین واریانسی صدق کند در غیر اینصورت آماره قابل محاسبه نخواهد بود.
نحوه محاسبه آماره و آزمون دوربین واتسون در نرمافزارهای محاسبات آماری
در بیشتر نرمافزارهای محاسبات آماری نظیر SAS ،SPSS و R محاسبه آماره دوربین واتسون وجود دارد در ادامه فهرستی از این نرمافزارها و دستور یا تابع محاسباتی این آماره معرفی شده است.
- زبان برنامهنویسی محاسبات آماری R: تابع dwtest از کتابخانه lmtest یا تابع durbinWatsonTest یا (dwt) در کتابخانه car و نسخه داده پانلی این آماره با تابع pdwtest و pbnftest در کتابخانه plm قابل استفاده است.
- زبان برنامهنویسی متلب: با استفاده جعبه ابزار آمار (Statistics Toolbox) و تابع dwtest امکان محاسبه آماره آزمون دوربین واتسون وجود دارد.
- زبان و بسته نرمافزاری محاسبات آماری SAS: در این نرمافزار خروجی استاندارد مدل رگرسیونی در رویه model شامل آماره دوربین واتسون است همچنین اگر از رویه (Procedure) رگرسیون خطی reg استفاده کنید میتوانید گزینه dw را هم فعال کنید تا آزمون دوربین واتسون اجرا شود.
- نرمافزار کاربردی اکسل: متاسفانه در اکسل تابعی برای انجام محاسبات مربوط به آماره دوربین واتسون وجود ندارد ولی به کمک فرمول زیر میتوانید این کار را انجام دهید. البته نحوه محاسبه آمار دوربین واتسون نیز در مثال ۱ مورد بررسی قرار گرفت.
- نرمافزار محاسبات آماری SPSS: هنگامی که از دستور رگرسیون خطی Linear Regression در SPSS استفاده میکنید امکان بهرهگیری از آزمون دوربین واتسون توسط فعال کردن دکمه Statistics وجود دارد.
همچنین در محیط کد نویسی SPSS نیز هنگام ایجاد مدل رگرسیونی میتوانید به عنوان یک انتخاب از آزمون دوربین واتسون کمک بگیرید. برای انجام این کار، کافی است از کدی به شکل زیر استفاده کنید.
- زبان برنامهنویسی پایتون: تابع durbin_watson در کتابخانه statsmodels وجود دارد و کافی است دستوری به صورت زیر را وارد کنید.
مثال ۲
در این مثال به بررسی آزمون دوربین واتسون در محیط SPSS میپردازیم. دادههای مثال ۱ را در نظر بگیرید. قرار است این مدل رگرسیونی را بوسیله SPSS اجرا و آزمون مربوط به وجود استقلال بین باقیماندهها را اجرا کنیم. میدانیم که مستقل بودن باقیمانده در مدل رگرسیونی، یکی از پیش شرطهای این گونه تحلیلها محسوب میشود.
نکته: اگر باقیمانده نرمال باشند، شرط عدم خودهمبستگی یا عدم همبستگی پیرسونی تبدیل به شرط استقلال میشود زیرا میدانیم اگر دو متغیر تصادفی مستقل با توزیع نرمال وجود داشته باشد، اگر ضریب همبستگی صفر باشد میتوان استقلال را نتیجه گرفت.
دادههای مثال ۱ را به صورت زیر در SPSS وارد کردهایم. برای دسترسی به تحلیل رگرسیون خطی نیز از فهرست Analysis گزینه Regression و سپس دستور Linear را انتخاب کردهایم. تنظیمات پنجره ظاهر شده مطابق با تصویر زیر است.
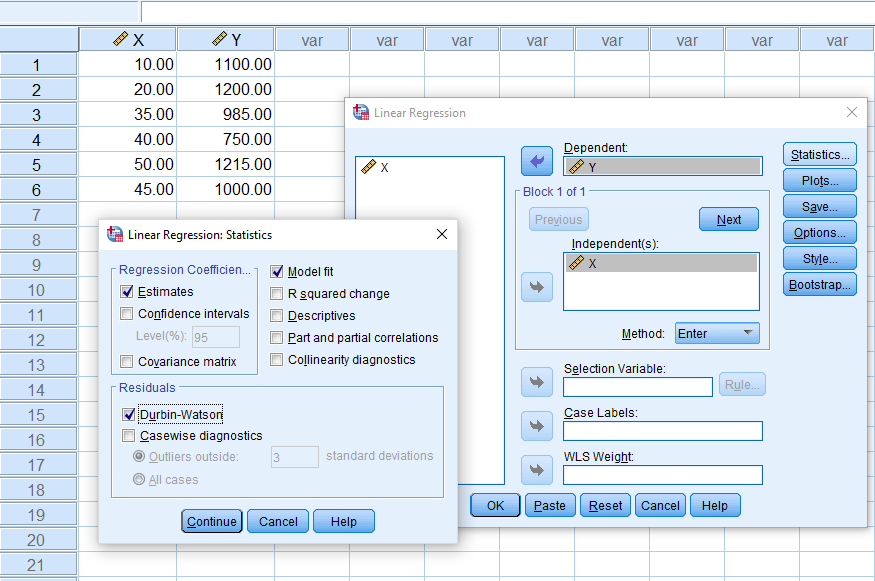
با تایید پارامترهای وارد شده توسط دکمه OK، خروجی مدل رگرسیونی به همراه آزمون دوربین واتسون ظاهر خواهد شد.

در جدول Model Summary خروجی تحلیل مربوط به مناسب بودن مدل ظاهر شده است. از آنجایی که ضریب تعیین () یا R Squared مقداری کوچک است به نظر میرسد که میزان سهمی از تغییرات متغیر وابسته که توسط مدل رگرسیونی بیان میشود بسیار کوچک است. از طرفی آماره دوربین واتسون نیز برابر با 2.77 است که بیانگر مستقل بودن باقیماندهها است. ولی با این وجود به نظر میرسد مدل رگرسیونی ارائه شده مناسب نیست.
همچنین مقدار Sig برای متغیر X در جدول Coefficients نیز بزرگتر از 0.05 بوده که نشانگر بیمعنا بودن این متغیر در مدل رگرسیونی است. پس اینطور به نظر میرسد حتی زمانی که آزمون دوربین واتسون بیانگر استقلال باقیماندهها است، نمیتوان یک مدل رگرسیون خطی بین متغیر و توسط این نمونه تصادفی ایجاد کرد.
خلاصه و جمعبندی
در این نوشتار با نحوه محاسبه آماره آزمون دوربین واتسون (Durbin-Watson) آشنا شدیم. همچنین به کمک مثالی نحوه محاسبه آماره این آزمون را فرا گرفتیم. قواعد تصمیم و نواحی بحرانی نیز برای آزمون دوربین واتسون ارائه و براساس یک مثال عددی نیز آزمون آماری را اجرا کردیم. همانطور که در تجزیه و تحلیل دادههای پانلی اشاره شد، یکی از روشهای بررسی وجود خودهمبستگی در داده پانلی، استفاده از آزمون دوربین واتسون است که محاسبات مربوط به این آزمون در تحلیلهای داده پانلی نیز در این متن مورد بررسی قرار گرفت. به این ترتیب با استفاده از آزمون دوربین واتسون، استقلال یا عدم وابستگی بین مشاهدات قابل سنجش است. البته برای مدلهای رگرسیونی و سری زمانی، شرط تصادفی بودن باقیمانده نیز باید مورد بررسی قرار گیرد. در دیگر نوشتار فرادرس به نام تصادفی بودن و آزمون گردش — به زبان ساده به این موضوع نیز پرداختهایم.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش SPSS
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای آمار و احتمالات
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
- فرایند تصادفی (Random Process) — مفاهیم اولیه
^^













سلام.
چطور میشه اثبات کرد که اگر در رگرسیون خوهمبستگی مثبت داشته باشیم، واریانس کمتر از مقار واقعی خودش نشون داده میشه؟
سوال دوم. اگر خودهمبستگی منفی داشتیم چطور باید رفعش کنیم؟