آزمون ناپارامتری میانه در آمار | به زبان ساده

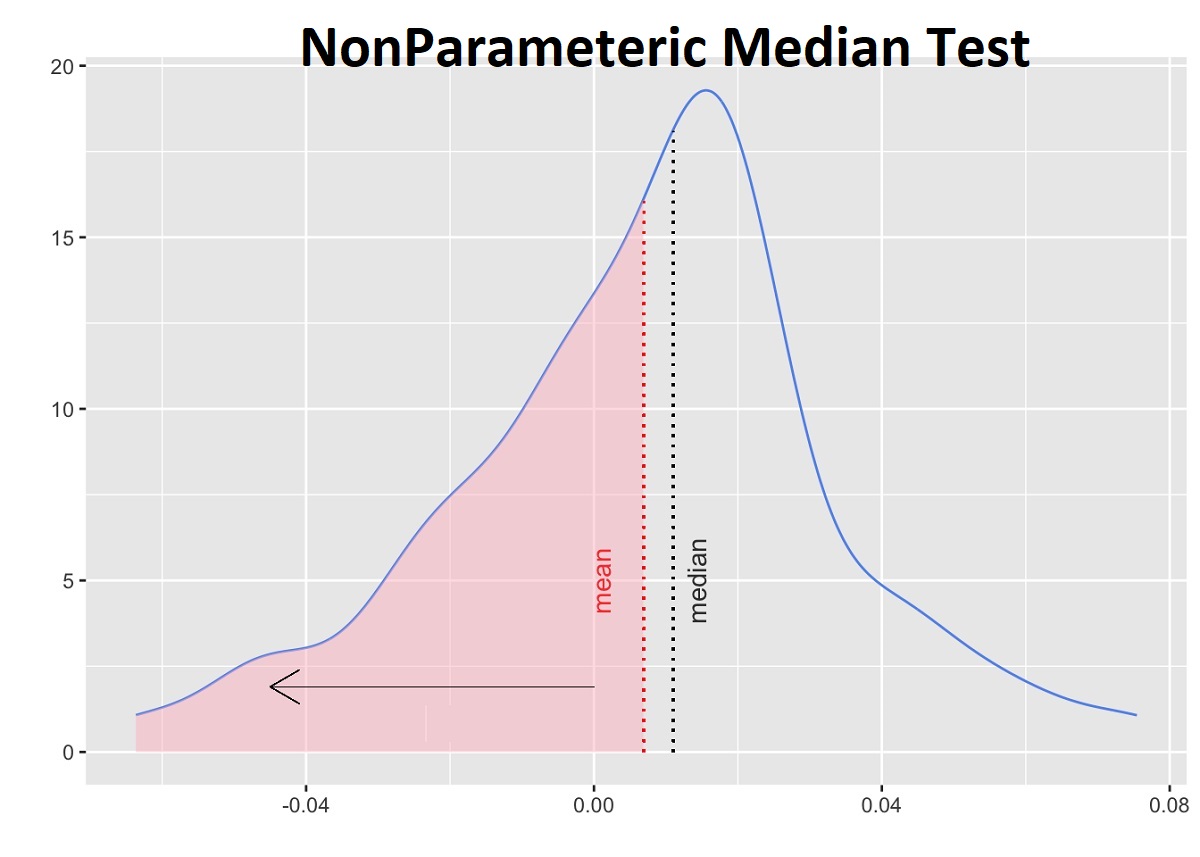
یکی از روش‌های آماری برای تحلیل داده‌ها، روش‌های ناپارامتری است که در اغلب موارد با فرضیه‌های کمتر نسبت به «روش‌های آمار پارامتری» (Parametric Methods) یا آمار کلاسیک، داده‌ها را تحلیل و آزمون فرض انجام می‌دهند. «روش‌های ناپارامتری» (Nonparameteric Methods) باید در مقابل «داده‌های پرت» (Outlier) مقاوم یا استوار باشند، بنابراین برای اندازه‌گیری شاخص تمرکز از «میانه» (Median) به جای «میانگین» (Mean) استفاده می‌شود. به همین دلیل محور اصلی در آزمون‌های ناپارامتری میانه یا «نما» (Mode) هستند. در این نوشتار به بررسی آزمون ناپارامتری میانه در آمار خواهیم پرداخت و با ذکر مثالی، نحوه اجرای آن را برای مقایسه دو جامعه آماری مرور و معرفی خواهیم کرد.

اگر می‌خواهید با آزمون‌های آماری و روش‌های ناپارامتری بیشتر آشنا شوید، بهتر است مطالب استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات و آمار پارامتری و ناپارامتری – انتخاب روش های تحلیل را مطالعه کنید. همچنین خواندن آزمون آماری مناسب در SPSS | راهنمای کاربردی و  مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری نیز خالی از لطف نیست.

آزمون ناپارامتری میانه در آمار

از «آزمون میانه» (Median Test) برای آزمایش اینکه آیا دو گروه از نظر مقدار میانه متفاوت هستند یا خیر، استفاده می‌شود. در حقیقت اختلاف در دو جامعه به جای مقایسه میانگین، برحسب میانه آن‌ها سنجیده می‌شود. به زبان ساده، آزمون میانه بر این موضوع تمرکز خواهد کرد که آیا دو گروه یا دو جامعه مستقل، دارای میانه‌های مختلف هستند و در نتیجه می‌توان آن‌ها را از لحاظ ساختاری، مجزا و تفاوتشان را از لحاظ آماری، معنی‌دار در نظر گرفت.

فیلم آموزش آزمون آماری ناپارامتریک و اجرای آن با SPSS – ویژه مدیریت و علوم انسانی در فرادرس

کلیک کنید

در نوشتارهای مجله فرادرس با روش‌های ناپارامتری دیگر نظیر آزمون علامت (Sign Test) نیز آشنا شده‌اید. در آنجا هم به جای استفاده از مقادیر، از علامت اختلاف‌ها یا رتبه‌ها استفاده می‌شود. بنابراین انتظار داریم که در آزمون ناپارامتری میانه نیز از رتبه‌بندی مقادیر برای سنجش یا ساختن آماره آزمون بهره ببریم.

هر چند در مورد توزیع یا بررسی نقاط پرت در این آزمون شرط‌هایی وجود ندارد ولی باید به دو نکته مهم در رابطه با این آزمون توجه داشت. فرض اولیه بر این موضوع استوار است که مشاهدات حاصل از نمونه‌های تصادفی بوده و هم توزیع هستند. هر چند ممکن است مقدار پارامتر (مثلا میانه) برای هر دو جامعه متفاوت باشد ولی معیارهای دیگری که شاید باعث اختلاف دو جامعه می‌شوند (مثلا واریانس یا پراکندگی) باید در بین آن‌ها یکسان در نظر گرفته شود. بنابراین تنها مشخصه‌ای که باعث ایجاد اختلاف در ساختار دو جامعه بوده از نابرابری میانه‌های (یا معیار تمرکز) آن‌ها نشات گرفته است. این عبارت‌ها، فرض اولیه را توجیه می‌کند.

دومین شرط نیز در اینجا کمّی بودن متغیر مورد بررسی است. به این ترتیب می‌توان میانه را برای چنین مقادیری محاسبه کرد. البته به یاد دارید که برای داده‌های کیفی که به صورت ترتیبی باشند نیز محاسب میانه امکان‌پذیر است. بنابراین شرط را گسترش داده و فرض می‌کنیم که متغیر اندازه‌گیری شده در بین دو جامعه، کمّی یا کیفی و با مقیاس ترتیبی است.

در ادامه با مثالی آشنا می‌شویم تا به ما در درک صحیح عملکرد و نحوه اجرای آزمون ناپارامتری میانه کمک کند.

معرفی مثال برای اجرای آزمون ناپارامتری میانه

برای بررسی آزمون میانه، یک بانک خصوصی را در نظر بگیرید که علاقمند است دریابد که آیا دو طبقه یا گروه از مشتریان از نظر رضایت از خدمات، نظر یکسانی دارند یا خیر. رضایت از خدمات بانکی، در بین گروه افرادی که دارنده حساب پس‌انداز هستند و کسانی که از خدمات حساب جاری بهره می‌برند، سنجیده و اندازه‌گیری شده است.

یک نمونه تصادفی از 20 مشتری از هر گروه با توجه به برداشت آنها از کیفیت خدمات بانک با استفاده از میزان رضایت به صورت درصدی و با مقیاس ترتیبی جمع‌آوری و در جدولی ثبت شده است. نمره یا «امتیاز 1» نشانگر «بسیار ناراضی» و «نمره 100» نیز بیانگر «بسیار راضی» است. نمرات جمع آوری شده برای هر پاسخ دهنده در هر گروه در جدول شماره ۱ دیده می‌شود.

جدول 1: امتیاز رضایت از خدمات بانکی برای مشتریان دو گروه حساب جاری و پس‌انداز

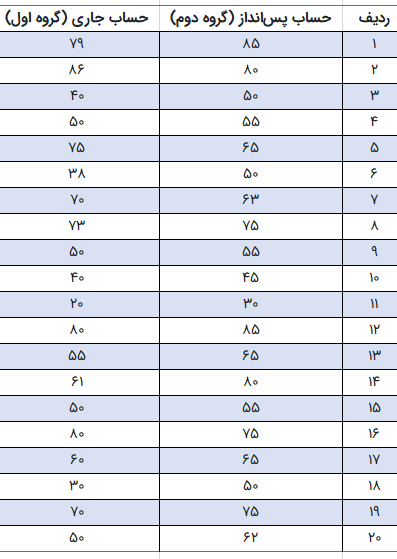
با توجه به این داده‌ها، در مورد میزان رضایت بین این دو گروه چه قضاوتی دارید. آیا هر دو گروه از خدمات بانکی رضایت یکسانی دارند؟ برای پاسخ به این سوال دست به یک آزمون آزمون آماری از نوع ناپارامتری می‌زنیم. واضح است که با توجه به کمبود تعداد نمونه‌ها، نمی‌توانیم توزیع را نرمال در نظر گرفته و از آزمون Z یا آزمون t استفاده کنیم.

رتبه‌ها و محاسبه آماره آزمون ناپارامتری میانه

اولین کار در آزمون میانه بدست آوردن «میانه کلی» (Grand Median) است. داده‌های ترکیب شده از هر دو گروه را به ترتیب نزولی مرتب کنید. یعنی آن‌ها را از بزرگترین به کوچکترین مقدار مرتب کرده و به هر یک رتبه بدهید. در این حالت، میانه کلی، معدل مقدار بیستم و بیست و یکم از مشاهداتی است که به ترتیب نزولی مرتب شده‌اند. در رابطه‌ای که در ادامه مشاهده می‌کنید، این مقادیر به صورت $$X_{(20)}$$ و $$X_{(21)}$$ نشان داده شده است. با توجه به رابطه‌های زیر، میانه کلی برابر با ۶۱٫۵ خواهد بود.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS در فرادرس

کلیک کنید

به یاد دارید که محاسبه میانه ($$m$$) برای تعداد مشاهدات زوج (در اینجا n = 20 + 20 = 40) به صورت زیر بدست می‌آید.

$$ \large m = \dfrac{X_{( \frac{n}{2}) } + X_{ (\frac{n}{2} + 1)} } {2}$$

پس خواهیم داشت:

$$ \large m = \dfrac{X_{( 20) } + X_{ (21)} } {2} = \dfrac{62 + 61 }{2} = 61.5 $$

نکته: اگر داده‌ها دارای «رتبه‌های گره دار» (Tied Rank) هستند، میانگین رتبه‌ها را در نظر بگیرید.

در جدول شماره ۲، مقادیر مرتب شده به صورت نزولی و رتبه‌های آن‌ها دیده می‌شود. البته باید توجه داشت که این جدول را می‌توانستیم براساس مقادیر مرتب شده صعودی نیز تشکیل دهیم. روال کار برای پیدا کردن آماره آزمون و انجام آزمون دقیقا مشابه با حالت مرتب‌سازی نزولی خواهد بود.

جدول ۲: مقادیر مرتب شده و رتبه‌های گره‌دار برای میزان رضایت از خدمات بانکی

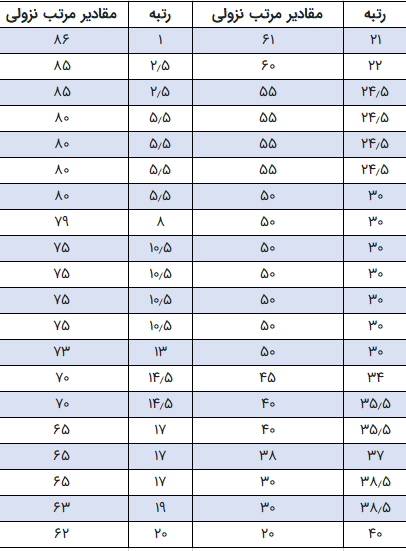
در بخش بعدی با توجه به مقادیر مربوط به رضایت، یک «جدول توافقی» (Contingency Table) از تعداد مشاهداتی تشکیل می‌دهیم که در هر گروه از میانه کل بیشتر یا کمتر هستند. چنین کاری را در جدول ۳، مشاهده می‌کنیم. البته هر کدام از خانه‌های داخلی این جدول را به صورت a,b,c,d نام‌گذاری کرده و برحسب آن‌ها محاسباتی انجام داده‌ایم تا به آماره آزمون ناپارمتری میانه برسیم.

جدول ۳- شمارش مشاهدات بیشتر و کمتر از میانه کل در هر گروه

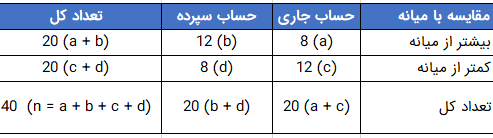
پس از انجام محاسبات طبق جدول ۳، آماره آزمون طبق رابطه زیر محاسبه می‌شود. این آماره که به نماد $$\chi^2$$ نشان داده شده، به طور مجانبی دارای «توزیع کای ۲» (Chi-square Distribution) بوده و طبق جدول‌های این توزیع مقادیر بحرانی آن محاسبه می‌شود.

$$ \large \chi^2 = \dfrac{n \left( \mid ad - bc \mid - \dfrac{n}{2} \right) ^2}{(a + b)(c + d)(a + c)(b + d) }$$

بعد از جایگذاری مقادیر a,b, c  و d در فرمول یاد شده، به مقدار ۰٫۹۰ خواهیم رسید.

$$ \large \chi^2 = \dfrac{40( 80 - 20) ^2}{(20)(20)(20)(20) } = 0.90 $$

توجه داشته باشید که در آزمون ناپارامتری میانه فرضیه‌های صفر و مقابل به صورت زیر در نظر گرفته می‌شوند.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

فرضیه صفر: در سطح رضایت اندازه‌گیری شده تفاوتی بین دارندگان حساب جاری و دارندگان حساب پس انداز وجود ندارد.

فرضیه مقابل: بین دارندگان حساب جاری و دارندگان حساب پس انداز در سطح رضایت تفاوت معنی‌داری وجود دارد.

انتظار داریم که اگر هر دو گروه از لحاظ رضایت، مقدار یکسانی را بیان می‌کردند، آماره آزمون ناپارامتری میانه کوچک باشد، ولی اگر آماره آزمون از صدک بالایی مربوطه به توزیع کای ۲، با توجه به سطح خطای آزمون، یعنی $$\alpha = 0.05$$، بزرگتر باشد، فرض صفر را رد خواهیم کرد.

با توجه به جدول توزیع کای ۲، در سطح ۰٫۰۵ و درجه آزادی $$(k - 1) (r - 1) = (2 - 1)(2 - 1) = 1 $$ فرض صفر رد نمی‌شود، بنابراین با توجه به نمونه ارائه شده، دلیل کافی برای رد فرض صفر در اختیار نداریم.

$$ \chi^2_{1 - \alpha}(df) = \chi^2_{0.95}(1) = 3.84$$

توجه داشته باشید که  درجه آزادی توسط رابطه $$df = (k - 1 ) (r - 1)$$ محاسبه شده که در آن $$k$$ تعداد ستون‌ها و $$r$$ تعداد سطرهای جدول توافقی گفته شده است.

خلاصه و جمع‌بندی

در این نوشتار با آزمون ناپارامتری میانه و کاربردهای آن آشنا شده و نحوه محاسبه آماره آزمون را براساس رتبه‌های مربوط مقادیر دو جامعه مستقل نشان دادیم. از آنجا که این آزمون در گروه روش‌های ناپارامتری قرار دارد، به جز تصادفی و هم توزیع بودن نمونه‌های هر گروه، شرط دیگری نداریم. همانطور که دیده شد، این آزمون محاسبات ساده‌ای داشته و توزیع آماره آزمون مربوطه نیز براساس جدول‌های اکثر کتاب‌های آمار ناپارامتری مشخص شده است. البته توان آزمون‌های مشابه مانند آزمون ویلکاکسون بیشتر از آزمون میانه است.