آزمون مقایسه میانگین ها در SPSS | راهنمای گام به گام
استنباط آماری معمولا به وسیله آزمون فرض آماری شناخته میشود. براساس این روش آماری، به کمک نمونهگیری از جامعه آماری و اطلاعات بدست آمده، به یک تصمیم در مورد پارامتر جامعه آماری میرسیم. اغلب برای نمونههای بزرگ، از نرمافزارهای رایانهای مانند SPSS برای انجام محاسبات استفاده میکنند. به این منظور در این نوشتار از مجله فرادرس نیز به بررسی آزمون مقایسه میانگین ها در SPSS خواهیم پرداخت. با توجه به اینکه واریانس جامعه آماری از قبل مشخص نیست، توزیع آماره آزمون در این حالت با توزیع t یکسان در نظر گرفته شده و چنین آزمونهایی را آزمون t مینامند.
به منظور آشنایی بیشتر با اصطلاحات و نحوه اجرای آزمون آماری مربوط به میانگین جامعه، مطالب دیگر مجله فرادرس مانند آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و آزمون فرض میانگین جامعه در آمار — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتار مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری و آزمون تی (T Test) در R — راهنمای کاربردی نیز خالی از لطف نیست.
آزمون مقایسه میانگین ها در SPSS
قبل از هر چیز، باید مشخص کنیم که هدف از اجرای آزمون مقایسه میانگین در SPSS چیست. فرض کنید یک نمونه از جامعه آماری با توزیع نرمال، در اختیارتان قرار گرفته است و باید در مورد پارامتر میانگین چنین جامعهای دست به قضاوت بزنید. البته از قبل، بوسیله اطلاعاتی که در اختیارتان قرار گرفته، حدسهایی در مورد میانگین جامعه، دارید ولی میخواهید بدانید که این حدس، چقدر با واقعیتی که نمونه آماری برایتان رقم زده است، هماهنگ است. در حقیقت میخواهید مشخص کنید که آیا بین میانگین حدسی و میانگین جامعه، اختلاف آماری وجود دارد یا خیر. این کار را به کمک نرمافزار و اجرای آزمون مقایسه میانگین ها در SPSS انجام خواهیم داد.
به این منظور، میانگین حدسی و نمونه جمعآوری شده را به بوته آزمایش میسپاریم که این کار در آمار به آزمون فرض آماری مشهور است. واضح است که نتیجه گرفته شده، وابسته به شانس و تصادف است زیرا نتیجه و مشاهدات، از یک نمونه به نمونه دیگر، تفاوت خواهند داشت. ولی میخواهیم کاری کنیم که اختلاف مشاهده شده بین میانگین حدسی و میانگین نمونه، بتواند به عنوان یک متغیر تصادفی در نظر گرفته شده و براساس آن آماره آزمون و ناحیه بحرانی (Critical Area) را به کمک حداکثر خطای نوع اول (Error Type I)، بسازیم. این همان کاری است که قرار است نحوه اجرای آزمون مقایسه میانگین ها در SPSS را به ما آموزش دهد.
آزمون مقایسه میانگین یک جامعه با مقدار ثابت در SPSS
همانطور که گفته شد، اجرای آزمون آماری، نیاز به یک آماره آزمون و ناحیه بحرانی دارد. زمانی که با یک جامعه نرمال مواجه هستیم و میخواهیم در مورد میانگین آن دست به قضاوت بزنیم، آماره آزمون به صورتی که در رابطه ۱ دیده میشود، قویترین یا «پرتوانترین آزمون» (Most Powerfull Test) را برایمان به ارمغان میآورد.
رابطه ۱
در رابطه ۱، میانگین نمونه، مقدار حدسی برای میانگین و انحراف استاندارد نمونه بوده که برآوردی برای انحراف معیار جامعه است. واضح است که در این رابطه، تعداد نمونه یا مشاهدات گرفته شده از جامعه آماری است. به این ترتیب، آماره آزمون در این حالت دارای توزیع t با n-1 درجه آزادی (Degree of Freedom) است. یعنی داریم:
رابطه ۲
نکته: زمانی که با یک جامعه آماری نرمال و مشاهدات تکی مواجه هستیم، آماره آزمون مربوط به رابطه ۱، پرتوانترین آزمون پارامتری را در اختیارمان قرار میدهد. ولی اگر از نرمال بودن جامعه، اطلاعی نداشته باشیم یا فرض نرمال بودن جامعه توسط آزمونهای نرمالیتی رد شود، آزمونهای ناپارامتری مانند آزمون ویلکاکسون (Wilcoxon)، دارای توان بیشتری خواهند بود.
اگر میانگین جامعه را و مقدار حدس زده شده را با نشان دهیم، فرضیات یعنی «فرض صفر» (Null Hypothesis) و «فرض مقابل» یا «فرض یک» (Alternative Hypothesis) مربوط به آزمون تک نمونهای، به صورت زیر نوشته میشوند.
رابطه ۳
توجه داشته باشید که در اینجا آزمون دو طرفه (Two-Tailed) است. به این معنی که ناحیه بحرانی، هم شامل مقادیر بزرگتر و هم کوچکتر از یک مقدار مشخص است. واضح است که در آزمون دو طرفه، «فرض صفر» (Null Hypothesis) یا بیان میکند، میانگین جامعه با مقدار حدسی برابر است در حالیکه «فرض مقابل» یا «فرض مخالف» (Alternative Hypothesis) نابرابری بین این دو مقدار را نشان میدهد. اغلب، فرض صفر را به عنوان گزارهای به صورت «میانگین جامعه با مقدار برابر است» در نظر گرفته و فرض مقابل را گزارهای به شکل «میانگین جامعه با مقدار برابر نیست» مشخص میکنیم.
نکته: آزمونهای یک طرفه نیز به شکلی به کار میروند که فرض مقابل فقط به یک ناحیه از مقادیر پارامتر جامعه اشاره دارد. برای مثال یا اگر در فرض مقابل به کار روند، آزمون یک طرفه خواهد بود.
برای دسترسی به آزمون مقایسه میانگین با مقدار ثابت در SPSS از مسیر زیر اقدام میکنیم.
Analyze - Compare Means - One-sample T Test
کافی است متغیر مورد آزمون را در کادر Test Variable قرار داده و مقدار حدسی برای میانگین را در کادر Test Value وارد کنید.
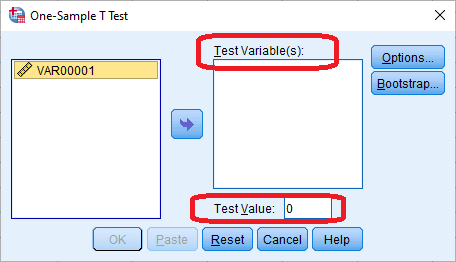
با کلیک بر روی دکمه OK، آزمون اجرا شده و نتیجه در خروجی ظاهر خواهد شد. برای آشنایی بیشتر با این آزمون و تفسیر خروجیها، بهتر است نوشتار آزمون میانگین نمونه تکی در SPSS — راهنمای کاربردی از مجله فرادرس را مطالعه کنید.
آزمون مقایسه میانگین ها در SPSS برای دو جامعه مستقل
گاهی به کمک آمار و آزمون فرض، میخواهیم براساس دو نمونه تصادفی، یکسان بودن ویژگی در بین دو جامعه را مورد تحقیق قرار دهیم. در حقیقت اگر را میانگین جامعه اول و را میانگین جامعه دوم در نظر گرفته باشیم، به کمک این روش میخواهیم آزمون فرض زیر را انجام دهیم.
رابطه ۴
البته میتوان با تغییراتی در ظاهر مسئله، آن را به یک آزمون تک نمونهای تبدیل کرد. به رابطه زیر دقت کنید.
رابطه ۵
آماره آزمون (T) در این حالت طبقه رابطه ۶ خواهد بود.
رابطه ۶
که در آن میانگین نمونه اول (مربوط به جامعه اول) و میانگین نمونه دوم (مربوط به جامعه دوم) است. مخرج این کسر نیز برآورد انحراف معیار آمیخته دو جامعه را نشان میدهد. در حالتی که شرط برابری واریانسها (مثلا توسط آزمون لون- Leven's Test) در دو جامعه مورد تایید قرار گیرد، مقدار واریانس آمیخته از رابطه زیر حاصل میشود.
رابطه ۷
مشخص است که و به ترتیب تعداد مشاهدات نمونه از جامعه اول و دوم هستند. همچنین و نیز برآورد واریانس برای هر یک از جوامع محسوب میشوند.
در صورتی که شرط برابری واریانسها برقرار نباشد، واریانس آمیخته را برحسب رابطه ۸، محاسبه خواهیم کرد.
رابطه ۸
نکته: میدانید که محاسبه ریشه دوم از واریانس، همان انحراف معیار نامیده میشود. بنابراین کافی است از ، جذر گرفته و حاصل را در مخرج رابطه مربوط به محاسبه آماره آزمون، قرار دهیم.
توزیع این آماره نیز توزیع تی (T- Distribution) است ولی درجه آزادی () آن به صورت زیر بدست میآید.
رابطه ۹
برای دسترسی به آزمون مقایسه میانگین ها در SPSS برای دو جامعه مستقل از مسیر زیر اقدام کنید.
Analyze - Compare Means - Independent-Samples T Test
با اجرای این دستور، پنجرهای مطابق با تصویر ۲، ظاهر شده که در آن باید پارامترهای مربوط به «متغیرهای آزمون» (Test Variable) و «متغیر گروه بندی» (Grouping Variable) را مشخص کنید.
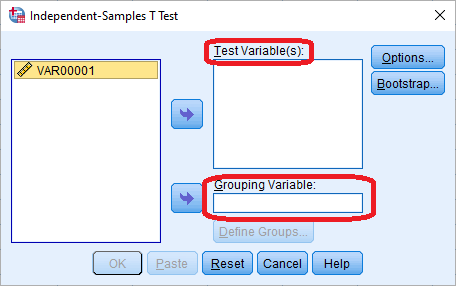
توجه داشته باشید که پس از معرفی متغیر گروهبندی و قرار دادن آن در کادر مربوطه، با دکمه Define Groups، مقادیری را معرفی کنید دستهها را مشخص میکند. اگر متغیر مربوطه، فقط دارای دو سطح یا مقدار متفاوت است، اولی را در قسمت Group1 و دومی را در Group2 وارد کنید. البته اگر بیش از دو مقدار برای چنین متغیری وجود داشته باشد، با مشخص کردن دو مقدار اصلی، مقایسه میانگینها برای این دو گروه صورت خواهد گرفت.
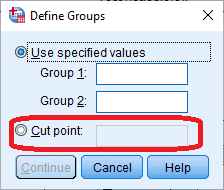
همچنین میتوانید با تعیین یک مقدار آستانه، مقادیر متغیر گروهبندی را به دو دسته تفکیک کنید. گروه اول مقادیری است که از آستانه کمتر بوده و دسته دوم، مقادیری که از آستانه بزرگتر یا مساوی باشند. به تصویر ۳ توجه کنید. گزینه یا کادر Cut point، آستانه یا نقطه بُرش را برای تبدیل متغیرهای کمی به طبقهای تعیین میکند.
به این موضوع توجه کنید که در این حالت، نرمافزار SPSS دو گونه خروجی ارائه میدهد. در یک سطر، محاسبات را براساس فرض تساوی واریانسها انجام داده و مقدار p-value را گزارش مینماید. در سطری دیگر، با فرض نابرابری در بین واریانسها، آزمون T را اجرا کرده و خروجی را تولید میکند.
البته آزمون مربوط به برابری واریانسها نیز در ابتدا ظاهر شده، تا کاربر با توجه به میزان احتمال خطای نوع اول، نسبت به رد یا تایید فرض صفر برای واریانسها، اقدام کرده، سپس به سطر اول یا دوم برای دریافت نتیجه آزمون مقایسه میانگین ها در SPSS بپردازد. در تصویر ۴، نمونهای از خروجی این آزمون را مشاهده میکنید، بخش مربوط به آزمون واریانس و آزمون میانگینها در این تصویر مشخص شده است.
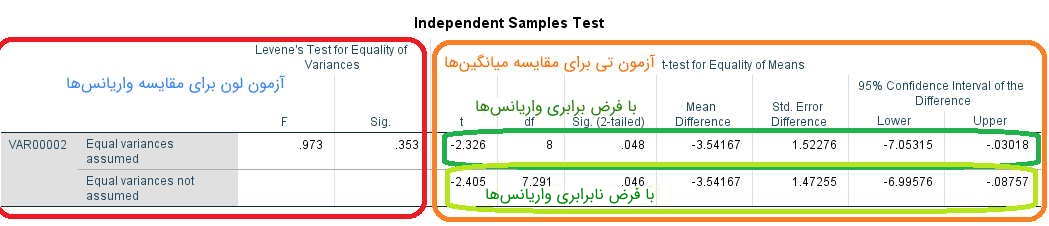
همانطور که در تصویر ۴ به عنوان نتیجه آزمون مقایسه میانگین ها در SPSS برای دو جامعه مستقل، مشاهده میکنید، کادر قرمز رنگ مربوط به آزمون لون و مقایسه واریانسها است. از آنجایی که مقدار Sig برابر با ۰٫۳۵۳ بوده و بزرگتر از ۰٫۰۵ است، فرض برابری واریانسها رد نشده و باید به سطر اول جدول آزمون تی توجه کنیم. در اینجا هم با توجه به مقدار Sig (آزمون دو طرفه) که برابر با ۰٫۰۴۸ و کوچکتر از سطح خطای نوع اول ۰٫۰۵ است، فرض برابری میانگینها رد خواهد شد. در انتهای جدول نیز، فاصله اطمینان شامل نقطه صفر نبوده که باز هم دلیلی بر رد فرض صفر خواهد بود.
آزمون مقایسه میانگین ها در SPSS برای مشاهدات زوجی
نوع دیگری از آزمونهای مقایسه میانگین ها در SPSS مربوط به مقایسههای زوجی است. به این معنی که تعداد مشاهدات در هر دو گروه با هم برابر بوده و از طرفی مشاهدات به یکدیگر مرتبط هستند. برای مثال فرض کنید میخواهیم تاثیر یک دارو را روی یک بیماری (مثلا فشار خون) بسنجیم. از آنجایی که افراد از نظر جسمی با یکدیگر تفاوت دارند، بهتر است درمان را روی دو گروه همسان (مثلا دوقلوها) انجام دهیم تا تفاوتهای مشاهده شده بین گروه تیمار (Treatment) و کنترل (Control)، فقط به علت مصرف دارو باشد. بنابراین برای گروه اول (تیمار) که دارو مصرف کرده با گروه کنترل که دارونما (Placebo) مصرف کرده یا بدون مصرف دارو، فشار خونها اندازهگیری شده و تفاوت مصرف دارو را روی کاهش فشار خون اندازهگیری میکنیم.
گاهی این روش استنباط آماری را به پیشآزمون (Before Test) و پسآزمون (After Test) نیز میشناسند. افراد، قبل از خوردن دارو، فشار خونشان اندازهگیری شده و پس از مصرف نیز مورد اندازهگیری واقع میشود. وجود اختلاف آماری در بین مقادیر قبل و بعد، نشان از موثر بودن دارو فشار خون دارد.
فرضیههای این آزمون درست به مانند (رابطه ۴ یا ۵) نوشته شده و آماره آزمون نیز به صورت زیر خواهد بود.
رابطه ۱۰
توجه داشته باشید که در رابطه ۱۰، ، اختلاف مقادیر نمونههای زوج اول از دوم است و نیز انحراف معیار این اختلافها محسوب میشود. از آنجایی که مشاهدات به صورت زوج مرتب هستند، ، تعداد زوجها را مشخص میکند.
برای دسترسی به آزمون مقایسه میانگین ها در SPSS برای مشاهدات زوجی از مسیر زیر اقدام کنید.
Analyze - Compare Means - Paired-Samples T Test
به این ترتیب پنجرهای مانند تصویر 5 ظاهر شده که پارامترهای این آزمون که همان زوج متغیرها است را از شما درخواست میکند.
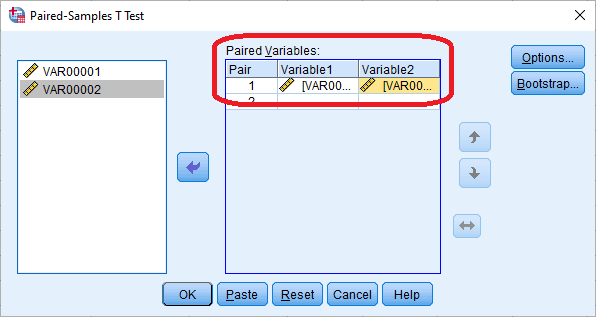
خروجیهای حاصل مانند تصویر ۶ ظاهر میشوند. باز هم با توجه به مقدار Sig نسبت به رد یا تایید فرض صفر اقدام میکنیم. در مثالی که در تصویر زیر، برای اجرای آزمون مقایسه میانگین ها در SPSS به صورت زوجی دیده میشود، با توجه به کوچک بودن مقدار Sig (تقریبا برابر با صفر)، فرض صفر در سطح خطای ۰٫۰۵ در میشود.

نکته: به یاد داشته باشید که در اینجا دو متغیر مورد آزمون قرار میگیرند. در حالیکه در آزمون نمونههای مستقل، دو گروه از مشاهدات تجزیه و تحلیل و برابری میانگین آنها، آزمون میشود.
آزمون مقایسه میانگین ها در SPSS برای چند جامعه مستقل
گاهی لازم است بین چند گروه یا جامعه، به بررسی شاخص میانگین بپردازیم. برای مثال فرض کنید میخواهیم میزان کاهش کلسترول خون را با دوزهای مختلف از یک دارو مشخص کنیم. قرار است به کمک یک آزمون آماری تشخیص دهیم که آیا تغییر دوز دارو، بر میزان کاهش کلسترول تاثیر گذار است یا تفاوتی بین دوزها وجود ندارد.
از آنجایی بیش از یک میانگین در این حالت مورد بررسی قرار میگیرد، نمیتوان از آزمونهایی مانند آزمون t و آمارههای مشابه استفاده کرد. روشی که «رونالد فیشر» (Ronald Fisher) پیشنهاد کرد، تجزیه واریانس کل به واریانسهای «درون گروهی» (Within-group Variation) و «بین گروهی» (Between-group Variation) است. به این ترتیب اگر میانگینها یکسان باشند، نسبت پراکندگی بین گروهی به کل پراکندگی کم بوده و بیشتر سهم پراکندی، توسط پراکندگی درون گروهی قابل توصیف است.
به همین علت، آماره آزمونی که در «تحلیل واریانس» (ANOVA) به کار میرود به صورت زیر خواهد بود. واضح است که این نسبت دارای توزیع F بوده و ناحیه بحرانی، با این توزیع مشخص میشود. جالب است که این آزمون براساس تفکیک پراکندگی صورت گرفته ولی برای قضاوت در مورد میانگین اجرا میشود.
که در آنها، و به صورت زیر محاسبه میشوند.
توجه داشته باشید که ، درجه آزادی صورت و درجه آزادی مخرج است.
فرضیههای مربوط به این آزمون به صورت زیر هستند.
بنابراین اگر تعداد جامعهها برابر با باشد، فرض صفر نشان میدهد که همه میانگینها یکسان هستند. بنابراین با فرض برابر بودن واریانسها، میتوان نتیجه گرفت که واقعا چندین جامعه وجود نداشته و همه یکسان هستند. در عوض فرض مقابل میگوید که بعضی از جوامع، دارای میانگین متفاوت با بقیه هستند. البته ممکن است تفاوت فقط در مورد یک جامعه برقرار باشد. به این ترتیب باز هم فرض صفر رد خواهد شد.
فرض کنید که سه جامعه مورد بحث باشند و بخواهیم میانگین آنها را با یکدیگر بوسیله آزمون مقایسه میانگین ها در SPSS به کمک آنالیز واریانس، اجرا کنیم. مجموعه دادهای، مطابق با تصویر ۷ را در نظر بگیرید.
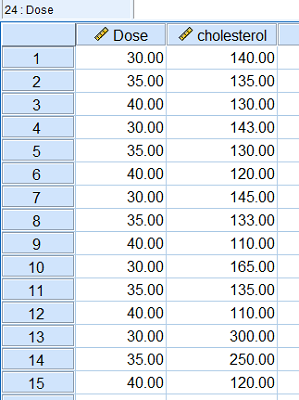
واضح است که متغیر Doze دارای سه سطح است و با اندازههای ۳۰، ۳۵ و ۴۰ مشخص شدهاند. به این ترتیب میتوانیم آن را به عنوان یک متغیر طبقهای در نظر بگیریم. از طرفی متغیر Cholesterol نیز متغیر کمی بوده که باید میانگین آنها را در هر سطح از میزان یا دوز دارو با یکدیگر مقایسه کرده و مورد آزمون قرار دهیم. به این منظور از مسیر زیر، دستور تحلیل واریانس در SPSS را اجرا میکنیم.
Analyze - Compare Means - One-way ANOVA
به این ترتیب پنجرهای به مانند تصویر ۸، ظاهر شده که کافی است تنظیمات را مطابق با آن انجام داده تا پاسخ را در خروجی SPSS مشاهده کنید.
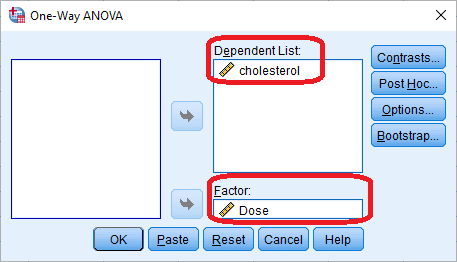
قسمت Dependent List، مخصوص قرار گرفتن متغیرهایی است که باید میانگین آنها مقایسه شود. همچنین بخش Factor برای تعیین متغیر گروهبندی است. پس از فشردن OK خروجی مطابق با تصویر ۹ ظاهر میشود.
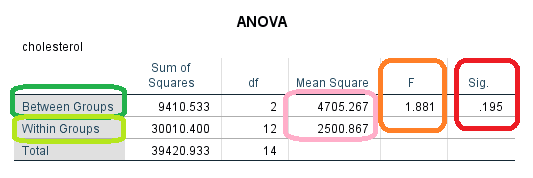
در هر بخش، میزان پراکندگی «درون گروهی» (Between Groups) و «بین گروهی» (Within Groups) دیده میشود. همانطور که در کادر صورتی رنگ مشاهده میکنید، میانگین مربعات پراکندگیهای بین گروهی نسبت به میانگین مربعات پراکندگی درون گروهی، مقدار بزرگی نیست. از طرفی در ستون Sum of Squares، مشخص است که مجموع مربعات درون گروهی، سهم بیشتری از کل پراکندگی را بیان کرده است. بنابراین باید فرض یکسان بودن گروهها را تایید کنیم.
توجه داشته باشید که مقدار F و Sig، به ترتیب، نشانگر ناحیه بحرانی و «پی مقدار» (p-Value) هستند. از آنجایی که مقدار F کوچک (۱٫۸۸۱) و Sig=۰٫۱۹۵، بزرگتر از ۰٫۰۵ است، فرض صفر رد نشده و نتیجه میگیریم که هر سه دوز، به یک میزان کلسترول خون را کاهش میدهند.
برای کسب اطلاعات بیشتر در مورد شرطهای اجرای آزمون مقایسه میانگین در SPSS بین چندین گروه مستقل، بهتر است این موضوع را در نوشتارهای آنالیز واریانس یک طرفه در SPSS | راهنمای کاربردی و تحلیل کوواریانس (چند متغیره) در SPSS — راهنمای کاربردی دنبال کنید.
خلاصه و جمعبندی
همانطور که در این متن خواندید، آزمون مقایسه میانگین ها در SPSS با توجه به ویژگیهای این نرم افزار به سادگی انجام شده و نتایج به راحتی قابل گزارش هستند. نکتهای که باید در هنگام به کارگیری این آزمون مورد نظر داشت، نرمال بودن توزیع جامعه آماری است تا به توان آزمون با بیشترین توان را اجرا کرد. در صورتی که چنین شرطی برقرار نباشد، آزمونهای ناپارامتری که به نرمال بودن توزیع جامعه آماری، توجهی ندارند، آزمونهای پرتوانتری محسوب شده و قابل استفاده هستند. کم بودن تعداد مشاهدات یا نمونه یکی از دلایلی است که ممکن است لزوم به کارگیری آزمونهای ناپارامتری محسوب شود. از طرفی چولگی زیاد در مشاهدات میتواند شرط نرمال بودن را از بین برده و ناگزیر به استفاده از آزمونهای ناپارامتری باشیم.
همچنین به یاد داشته باشید که مقایسه میانگین برای چندین جامعه، توسط تحلیل یا آنالیز واریانس صورت میگیرد. در نرمافزار SPSS، برای حالتی که فقط با یک متغیر طبقهای مواجه باشیم از «آنالیز واریانس یک طرفه» (One-way ANOVA) استفاده میشود. ولی اگر بیش از یک متغیر طبقهای باعث تفکیک جامعه شوند، میتوان از «آنالیز واریانس دو طرفه» (Two-way ANOVA) استفاده کرد.













با سلام در تایید فرض های آماری از طریق تحلیل مسیر، چه رابطه ای بین میانگین و انحراف معیار هست؟ انحراف معیار باید حدی داشته باشد که از آن بالاتر نرود. بعضی جاها دیدم که گفته شده حد آن از 0.9 بالاتر نباشد؟ ممنون
نمیدونم چجوری ازتون تشکر کنم فقط میتونم بگم خیلی ماهین
جای بی کفایتی مشاور آمارم رو برام پر کردین واقعا ممنونم .خدا خیرتون بده.
سلام
من میخاستم یک متغیر رو با یک معیار مقایسه کنم. برای اینکار اول باید از اون متغیر چارک بگیرم.
ولی در حالی که تعداد پرسشنامه مون 50 است. ولی تو خروجی چارک 25 فیصد شده 2 نفر، 50 فیصد شده 4 نفر و 75 فیصد شده 7 نفر.
به نظر تون مشکل در کجاست؟
سلام. لطف میکنید منبعی که مبحث آزمون مقایسه میانگی ها رو ازونجا ذکر کردید بفرمایید؟