تحلیل کوواریانس (چند متغیره) در SPSS — راهنمای کاربردی

در تحلیل مدل‌های خطی، روش‌های متعددی وجود دارد که برای تشخیص و مدل‌سازی ارتباط بین متغیر وابسته با متغیرهای مستقل به کار می‌رود. در این میان تحلیل کوواریانس یا ANCOVA که مخفف Analysis of Covariance است، تلفیقی از رگرسیون و تحلیل واریانس ANOVA است. در این نوشتار سعی داریم با مفاهیم اولیه مربوط به تحلیل کوواریانس ANCOVA و روش‌های محاسباتی آن در نرم‌افزار SPSS آشنا شده و با مثال‌هایی آن را بررسی کنیم.

برای کسب اطلاعات بیشتر در مورد محاسبات مربوط به تحلیل واریانس و شیوه تجزیه پراکندگی کل، بهتر است مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتار آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی نیز لازم به نظر می‌رسد. برای کسب دانش بیشتر در این زمینه نیز خواندن مطلب متغیر فاکتور (Factor) یا متغیر عامل در R — راهنمای کاربردی و تحلیل واریانس دو طرفه در پایتون — راهنمای گام به گام خالی از لطف نیست.

تحلیل کوواریانس (چند متغیره) در SPSS

اغلب زمانی که می‌خواهیم ارتباط بین یک متغیر عامل (Factor) با یک متغیر وابسته (Dependent) را مشخص کنیم از تحلیل واریانس استفاده می‌کنیم. ولی گاهی متغیر سومی نیز وجود دارد که بر متغیر وابسته اثر گذار است و باعث می‌شود که میانگین متغیر وابسته برای هر سطح از متغیر عامل تغییر کند، در حالیکه هدف تحقیق ما، اثری است که سطوح متغیر عامل (تیمارها) روی متغیر وابسته دارند. در این حالت متغیر سوم را مزاحم یا مداخله‌گر (Nuisance Variable) می‌نامند. از این جهت این تحلیل را به آنالیز کوواریانس می‌شناسند، که همبستگی و رابطه بین متغیر وابسته و مزاحم نیز مورد تحلیل قرار می‌گیرد.

فیلم آموزش تجزیه و تحلیل اطلاعات با نرم افزار SAS ساس

اینجا کلیک کنید

برای مثال اگر بخواهیم یک طرح آماری مربوط به اثر بخشی یک تیمار (پیش آزمون و پس آزمون) را در حضور یک متغیر مداخله‌گر بررسی کنیم از تحلیل کوواریانس استفاده خواهد شد. فرض کنید هوش افراد را بر اساس یک آزمون سنجیده‌ایم. حال برای ارزیابی اثر بخشی یک روش تدریس، افراد را به دو گروه تقسیم کرده‌ایم و به گروه اول (که گروه کنترل گفته می‌شود) به روش تدریس عادی و در گروه دوم نیز روش تدریس از راه دور برای انتقال مفاهیم و آموزش مورد استفاده قرار گرفته است. در پایان دوره از هر دو گروه آزمون ریاضی گرفته‌ایم. می‌خواهیم براساس حذف اثر هوش دانش‌آموزان اثر بخشی آموزش از راه دور را در یادگیری ریاضیات بسنجیم.

در آنالیز کوواریانس (ANCOVA) سعی داریم با ثابت نگه داشتن اثرات متغیر مزاحم، برابری مقدار میانگین متغیر وابسته را در سطوح مختلف متغیر عامل شناسایی کنیم. خوشبختانه متغیر مزاحم قابل اندازه‌گیری است و اغلب به صورت کمی در نظر گرفته می‌شود ولی متاسفانه نمی‌توانیم هنگام بررسی و اندازه‌گیری متغیر وابسته، اثر آن را حذف یا نادیده بگیریم. به این جهت تحلیل کوواریانس ANCOVA به بالا بردن دقت تحلیل‌های واریانس (ANOVA) کمک بسیاری می‌کند.

در تحلیل کوواریانس ANCOVA، پراکندگی کل متغیر وابسته به اجزای دیگری نظیر پراکندگی متغیر مزاحم، پراکندگی در هر سطح از متغیر عامل و پراکندگی خطای تصادفی تفکیک می‌شود. اگر متغیر وابسته را با $$y$$‌ و سطوح متغیر عامل را با $$\tau_i$$ و متغیر مزاحم را با $$x$$ مشخص کنیم مدل آنالیز کوواریانس ANCOVA به صورت زیر نوشته خواهد شد.

$$\large {\displaystyle y_{ij}=\mu +\tau _{i}+\mathrm {B} (x_{ij}-{\overline {x}})+\epsilon _{ij}}$$

رابطه ۱

همانطور که دیده می‌شود، رابطه ۱ بیانگر ارتباط خطی بین متغیرهای وابسته و مزاحم و همچنین متغیرهای عامل است. واضح است که در رابطه ۱، منظور از $$\mu$$‌ میانگین کل، $$y_{ij}$$ هم مشاهده $$j$$ام از سطح $$i$$ام متغیر عامل یا فاکتور است. $$\tau_i$$ هم اثر متغیر عامل در سطح $$i$$ام است که البته هدف برآورد یا آزمون در مورد آن‌ها است. به همین ترتیب $$\epsilon_{ij}$$‌ نیز خطا را نشان می‌دهد. $$x_{ij}$$‌ مقدار متغیر مزاحم را در سطح $$i$$ام فاکتور برای مشاهده $$j$$ام نشان می‌دهد. از طرفی $$\bar{x}$$ نیز میانگین کل متغیر مزاحم است. ضریب $$B$$ هم شیب خط رگرسیونی است که بین متغیر وابسته و متغیر مزاحم وجود دارد و رابطه خطی را بین آن دو مشخص می‌کند.

فرضیات مدل کوواریانس ANCOVA

در تحلیل کواریانس (ANOVA) برای متغیر وابسته و عامل فرضیاتی وجود داشت. در این جا هم همین فرضیات برای تحلیل کوواریانس باید صادق بوده و بعلاوه فرضیاتی نیز در مورد متغیر مزاحم خواهیم داشت. از آنجایی که از یک مدل رگرسیونی در آنالیز کوواریانس استفاده می‌شود، شرط‌های مربوط به صحت مدل رگرسیونی نیز باید مورد نظر قرار گیرد. همانطور که در تحلیل واریانس یک و دو طرفه گفته شد، شرطی که باید برای مولفه‌های متغیر عامل رعایت کرد صفر بودن مجموع آن‌ها است.

$$\large {\displaystyle \left(\sum _{i}^{a}\tau _{i}=0\right)}$$

• در مورد تحلیل کوواریانس نیز باید این شرط محقق شود. همچنین متغیر عامل باید طبقه‌ای (Categorical) باشد. متغیرهای وابسته و مزاحم نیز از نوع نسبی بوده و به صورت کمی بیان می‌شوند.
• مشابه تحلیل واریانس، در تحلیل کوواریانس نیز باید در هر سطح از متغیر عامل، توزیع متغیر وابسته نرمال یا نزدیک به نرمال باشد. از طرفی باید واریانس متغیر وابسته نیز در هر سطح از متغیر عامل، ثابت در نظر گرفته شود و تنها چیزی که ممکن است باعث تغییر در متغیر وابسته در هر سطح از متغیر عامل شود، تغییر در میانگین است.
• شرط تصادفی و مستقل بودن جمله یا عبارت خطا نیز باید مورد بررسی قرار گیرد.

تحلیل کوواریانس (ANCOVA) و کاربردهای آن

در ادامه حوزه و مسائلی را معرفی خواهیم کرد که روش آنالیز کوواریانس برای حل آن‌ها موثر واقع می‌شود.

• حوزه پزشکی
  •  آیا یک دارو بخصوص در درمان بیماری موثر است؟
  • آیا بین میانگین امید به زندگی بین دو گروه: دریافت کننده دارو، بدون مصرف دارو (گروه کنترل) از لحاظ آماری تفاوت معنی‌داری وجود دارد؟

همانطور که مشخص است، از تحلیل کوواریانس می‌توان برای تعیین اثر یک تیمار با کنترل یک متغیر دیگر (مثلا فشار خون قبل از اجرای تیمارها) کمک گرفت.

• حوزه جامعه شناسی
  • آیا افراد ثروتمند شادتر از گروه‌های دیگر هستند؟
  • آیا طبقات مختلف درآمدی، دارای میانگین متفاوت در سطح رضایت از زندگی از لحاظ آزمون فرض آماری هستند؟

این سوال‌ها را می‌توان با ANOVA نیز پاسخ داد. ولی آنالیز کوواریانس اجازه می‌دهد تا کنترل عامل مداخله‌گر یا مزاحم نیز صورت گیرد. به عنوان مثال با استفاده از حذف متغیر مزاحم سبک زندگی (Life Style)، می‌توان نتیجه دقیق‌تری از ارتباط خالص بین رضایت یا شادی با طبقات مختلف در‌آمدی کسب کرد.

• حوزه مطالعات مدیریتی
  • چه عاملی باعث سودآوری شرکت می‌شود؟
  • آیا چرخه استراتژی یک ، سه یا پنج ساله، باعث موفقیت شرکت در رسیدن به اهداف خود خواهد شد؟

اگر اندازه یا بزرگی شرکت و سرمایه آن را در تعیین ارتباط بین سودآوری و عامل نوع مدیریت به عنوان یک متغیر مداخله‌گر در نظر بگیریم، براساس آنالیز کوواریانس (ANCOVA)،  می‌توان انتخاب نوع استراتژی در موفقیت سازمان را مورد بررسی قرار داد و اثر بخشی هر یک از چرخه‌های استراتژی را تجزیه و تحلیل کرد.

کوواریانس یک طرفه در SPSS

آنالیز کوواریانس یک طرفه، بخشی از مدل‌های خطی عمومی (General Linear Model) یا GLM در SPSS محسوب می‌شود. در روش‌های GLM که توسط SPSS‌ قابل استفاده است، می‌توان از یک تا ۱۰ متغیر مداخله‌گر را در نظر گرفت. البته در بیشتر تحقیقات تعداد متغیرهای مداخله‌گر بیش‌ از ۳ متغیر نخواهد بود زیرا اندازه‌گیری بیش از ۳ متغیر مداخله‌گر هزینه‌های نمونه‌گیری را افزایش داده در حالی که ممکن است دقت در تحلیل را به میزان موثر تغییر ندهد. اگر چنین متغیر یا متغیرهایی وجود نداشته باشند و هیچ متغیر کمی، با متغیر وابسته همبسته نباشد، آنالیز کوواریانس همان نتایج تحلیل واریانس را نشان می‌دهد.

فیلم آموزش روش تحقیق – نحوه نگارش پایان نامه

اینجا کلیک کنید

در SPSS، دستور GLM اجازه می‌دهد تا مدل‌ فاکتورهای تصادفی را که جزئی از طرح ANCOVA نیستند نیز به کار گرفته شوند. برای اجرای صحیح روش GLM باید سطح سنجش یا مقیاس متغیرها (Measurement) در SPSS با دقت مشخص شده باشد.

در آنالیز کوواریانس یک طرفه، احتیاج به حداقل سه متغیر داریم که در ادامه معرفی و خصوصیاتشان در SPSS فهرست شده‌ است.

1. متغیر مستقل (Independent Variable): این متغیر کیفی بوده و به عنوان یک عامل در نظر گرفته می‌شود که باید از نوع اسمی (Nominal) یا رتبه‌ای (Ordinal) باشد. لازم به توضیح است که اگر تعداد متغیرهای عامل بیش از یکی در نظر گرفته شود، تحلیل کوواریانس دو یا چند طرفه خواهیم داشت.
2. متغیر وابسته (Dependent Variable): این متغیر کمی بوده و از نوع مقیاس (Scale) در نظر گرفته شود. به نظر می‌رسد که مقدار این متغیر با تغییر سطوح متغیر عامل، تغییرات مشخصی دارد. هدف از تحلیل کوواریانس یک طرفه نیز بررسی این تغییرات است. این متغیر باید دارای توزیع نرمال (نرمال چند متغیره) بوده و در هر سطح از متغیر عامل، دارای واریانس ثابت و برابر باشد.
3. متغیر مزاحم یا همبسته (Covariate Variable): این متغیر نیز به مانند متغیر وابسته از نوع کمی و از نوع مقیاس (Scale) می‌باشد. ولی منظور از تحقیق، اثر این متغیر نیست بنابراین آن را مزاحم می‌نامیم. گاهی این متغیر را به عنوان متغیر پیش‌آزمون نیز در نظر می‌گیرند.

براساس یک مثال که از میان مجموعه فایل‌های نمونه SPSS‌ انتخاب شده است، متغیرها و مراحل اجرای آنالیز کوواریانس یک طرفه را مرور کرده و نتایج را بررسی می‌کنیم. فایل نمونه را می‌توانید از مسیر زیر در SPSS فراخوانی کنید.

C:\Program Files\IBM\SPSS\Statistics\26\Samples\English\workprog.sav

در این فایل، دو شیوه و رویکرد به منظور افزایش درآمد افراد به کار گرفته شده است. ابتدا درآمد هر یک از کسب و کارها اندازه‌گیری شده و به عنوان متغیر مزاحم به کار می‌رود. متغیر درآمد بعد از اجرای رویکرد آموخته شده نیز برای هر دو روش اندازه‌گیری شده است. هدف این است که نشان دهیم که روش‌های افزایش درآمد با یکدیگر تفاوت دارند به شرطی که اثر درآمد قبل از به کارگیری روش‌های افزایش درآمد را حذف کرده باشیم.

متغیرها به صورت زیر نام‌گذاری شده‌اند.

1. متغیر مستقل: روش افزایش کسب درآمد با نام prog با دو سطح صفر و یک مورد استفاده قرار می‌گیرد. مثلا فرض کنید اگر مقدار متغیر prog برابر با ۱ باشد، روش تبلیغاتی اینترنتی مورد نظر بوده و اگر مقدار این متغیر برابر با صفر باشد، تبلیغات تلویزیونی به کار رفته است. واضح است که این متغیر از نوع طبقه‌ای و Nominal و در لیست متغیرهای SPSS، به صورت سه دایره تو در تو نشان داده شده است.
2. متغیر وابسته: درآمد بعد از اجرای طرح افزایش درآمد با نام incaft به عنوان متغیر وابسته در نظر گرفته شده که مخفف Income After است. همانطور که دیده می‌شود این متغیر کمی و از نوع Scale بوده و در پنجره متغیرهای SPSS با علامت خطکش نشان داده می‌شود.
3. متغیر مداخله‌گر یا Covariate: در این‌جا درآمد قبل از اجرای روش افزایش درآمد که با نام incbef مشخص شده است، متغیر مداخله‌گر در نظر گرفته شده. واضح است که این نام مخفف income before است که نشان از درآمد قبل از به کارگیری و اعمال سطوح متغیر عامل دارد. این متغیر نیز در لیست متغیرهای SPSS‌ با نماد خطکش مشخص شده است.

برای دسترسی به دستور GLM و پنجره تعیین پارامترهای آن از مسیر زیر اقدام کنید.

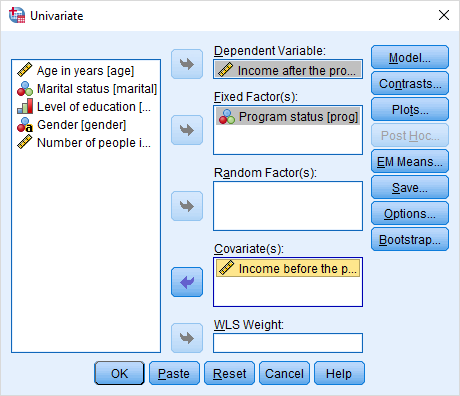
$$Analyze\rightarrow\;General\;Linear\;Model\rightarrow\;Univariate$$

تصویر زیر تنظیماتی که در این پنجره به منظور شناسایی متغیرها لازم است نشان داده شده است.

با کلیک بر روی دکمه Model، طرحی که برای آن می‌خواهید آزمون را انجام دهید، انتخاب می‌کنید. ساده‌ترین مدل به نام مدل اثرات اصلی (Main Effect) است که در آن فقط مدل‌سازی براساس متغیرهای عامل و متغیر مداخله‌گر به صورت مجزا صورت می‌گیرد ولی اگر لازم باشد که اثرات اصلی (Main Effect) متغیر عامل (روش کسب درآمد) را با حضور متغیر درآمد قبلی به طور هم‌زمان نیز بررسی کنیم، باید یک مدل اثرات متقابل (Interaction) نیز در نظر بگیریم. در تصویر زیر متغیر مداخله‌گر incbef به همراه متغیر prog و همچنین اثرات متقابل آن‌ها که به صورت incbef*prog نشان داده شده است، برای ایجاد مدل در نظر گرفته شده.

نکته: برای مشخص کردن هر دو متغیر و ایجاد یک مدل اثرات متقابل، باید هر دو متغیر (incbef‌ و prog) را انتخاب کنید و سپس گزینه Interaction را در قسمت (Build Term(s انتخاب کنید.

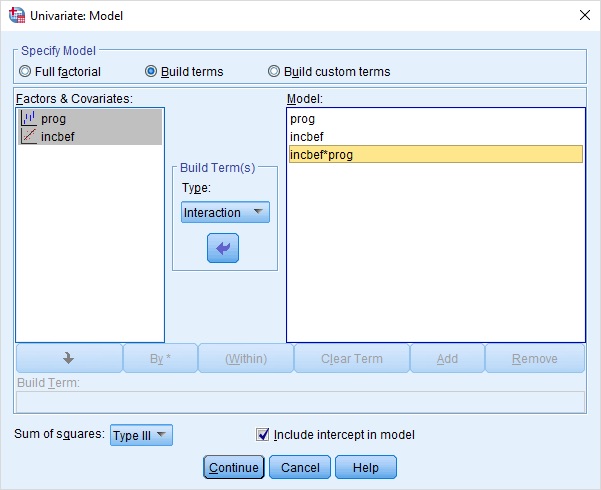
به این ترتیب مشخص می‌شود که آیا درآمد قبلی و نوع برنامه افزایش درآمد همزمان روی متغیر درآمد بعد از برنامه آموزشی موثر است یا خیر. پس از فشردن دکمه Continue به پنجره قبلی برگشته و برای انجام تحلیل بیشتر دکمه Options را کلیک کنید. پنجره‌ای به نام Options ظاهر می‌شود. کافی است تنظیمات را مطابق با تصویر زیر در آن انجام دهید تا فرضیات مربوط به صحت مدل تحلیل کوواریانس ANCOVA نیز صورت گیرد.

نکته: اگر بخواهید مدل بدون عرض از مبدا در نظر گرفته شود، با برداشتن انتخاب از گزینه Include intercept in model باعث می‌شوید که در رابطه 1‌ مقدار $$\mu\neq 0$$‌ فرض شود.

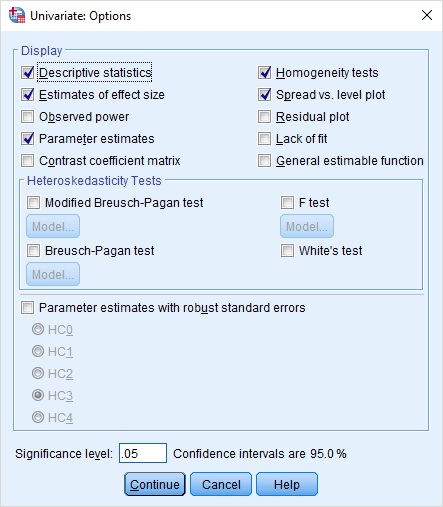
گزینه اولیه یا Descriptive statistics آماره‌های توصیفی مانند میانگین و انحراف معیار (Standard Deviation) را برای هر سطح از متغیر عامل نشان می‌دهد. گزینه Estimates of effect size برای نمایش و محاسبه اندازه اثر هر یک از متغیرهای عامل یا متغیر مداخله‌گر به کار می‌رود. همچنین برآورد پارامترهای $$B$$ در رابطه ۱ توسط گزینه Parameter estimates صورت می‌گیرد.

اگر بخواهیم ثابت بودن واریانس در بین گروه‌های تولید شده توسط متغیر عامل را نیز بررسی کنیم، گزینه Homogeneity tests و spread vs. level plot مناسب هستند. با فشردن دکمه Continue و بازگشت به پنجره اصلی، کافی است دکمه OK را کلیک کنید تا دستورات انجام و خروجی‌های آنالیز کوواریانس در پنجره Output ظاهر شوند.

تفسیر خروجی‌ها تحلیل کوواریانس (ANCOVA) یک طرفه در SPSS

پس از اجرای دستورات فوق، خروجی ظاهر خواهد شد. در ادامه هر قسمت از خروجی‌ها را تفسیر و نتیجه را گزارش می‌کنیم.

فیلم آموزش کنترل کیفیت آماری با اس پی اس اس SPSS

اینجا کلیک کنید

اولین قسمت از خروجی به علت درخواست مشاهده آماره‌های توصیفی Descriptive Statistics، مطابق با جدول زیر خواهد بود.

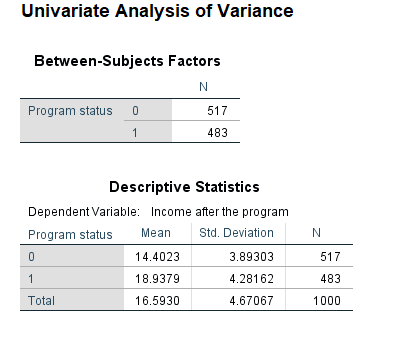
این جدول نشان می‌دهد که میانگین درآمد برای گروه prog=0 برابر با 14.40 و برای گروه prog=1 نیز با 18.93 برابر است. پس از لحاظ عددی این دو میانگین با یکدیگر اختلاف دارند. ولی آنچه انجام آزمون توسط تحلیل کوواریانس را ضروری می‌کند اختلاف در انحراف استاندارد Std. Deviation و اندازه یا حجم نمونه‌ها از هر دو گروه است زیرا این میانگین‌ها براساس 517 نفر از گروه صفر و 483 نفر از گروه یک بدست آمده که متاسفانه انحراف استاندارد گروه دوم نیز بزرگتر از گروه اول است. به همین علت است که باید توسط آزمون آماری بتوانیم اختلاف در نمونه‌ها را به اختلاف در جامعه نسبت دهیم.

از آنجایی که یکی از شرایط اجرای تحلیل کوواریانس ، برابر بودن واریانس در بین گروه‌ها است، SPSS یک آزمون لون (Leven's Test) برای بررسی این موضوع انجام داده است. جدول خروجی این آزمون در تصویر زیر دیده می‌شود.

با توجه به مقدار Sig که در انتهای جدول دیده می‌شود، به نظر می‌رسد که فرض برابری واریانس جمله خطا در سطح متغیر عامل، رد شده است زیرا $$sig=0.026<0.05$$ است. پس فرض صفر که برابری واریانس‌ها بود، رد خواهد شد. ولی شاید این موضوع زیاد اهمیت نداشته باشد زیرا اختلاف واریانس‌ها (انحراف معیارها) بسیار ناچیز است و می‌توان در تحلیل کوواریانس از آن صرف‌نظر کرد.

جدول بعدی در مورد اثرات متغیر عامل روی متغیر وابسته است که در حقیقت مدل تحلیل کوواریانس را بررسی می‌کند.

در اولین سطر این جدول، Corrected model قرار دارد که برآورد مجموع مربعات خطا را بدون در نظر گرفتن مقدار عرض از مبدا ($$\mu$$) نشان می‌دهد. به نظر می‌رسد با کوچک بودن مقدار $$sig$$ مدل مناسبی حاصل شده است. از طرفی اگر مقدار عرض از مبدا را صفر در نظر نگیریم، عامل prog با مقدار $$sig\approx 0 <0.05$$ روی تغییر میانگین متغیر وابسته تاثیر گذار است. همچنین بین متغیر incbef و incaft رابطه خطی برقرار است، به این معنی که با افزایش یکی، دیگری نیز افزایش می‌یابد. ولی از طرفی اثر متقابل متغیر عامل و متغیر مداخله‌گر وجود ندارد زیرا prog*incbef دارای $$sig=0.502$$ بزرگتر از $$0.05$$ است، پس فرض صفر بودن اثرش رد نشده و به نظر می‌رسد که همزمان این دو متغیر روی متغیر وابسته تاثیر گذار نیستند.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS

اینجا کلیک کنید

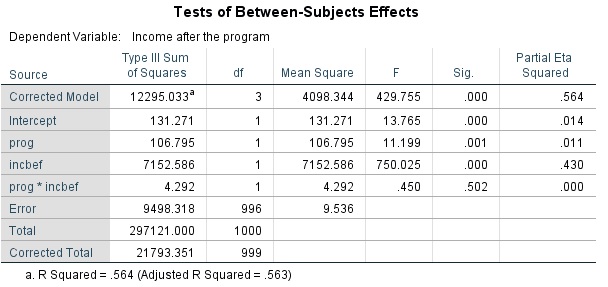
مقدار اثر (Effect Size) برای هر یک از این متغیرها نیز در ستون Partial Eta Squared در مدل تحلیل کوواریانس دیده می‌شود. هر چه مقدار این ستون برای هر یک از سطرها بیشتر باشد، تاثیر آن روی متغیر وابسته بیشتر است. مقدار «اتای جزئی مربع» (Partial Eta Squared) به صورت تقسیم تغییرات آن عامل به کل تغییرات حاصل می‌شود.

جدول بعدی به بررسی ضرایب مدل رگرسیونی در رابطه ۱ پرداخته است.

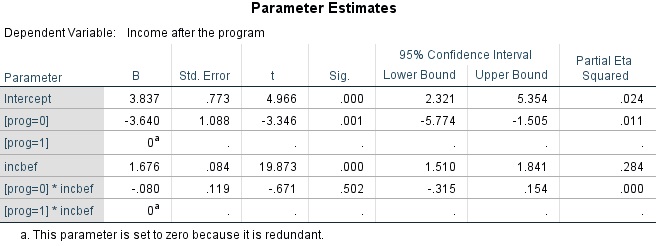
این طور به نظر می‌رسد که در هر سطح از متغیر عامل باید یک مدل رگرسیونی برای متغیر وابسته و متغیر مزاحم (Covariate) ایجاد شود. به همین علت هر سطح از متغیر عامل در ستون اول جدول دیده می‌شود.

عرض از مبدا (Intercept) برای مدل رگرسیونی برابر با 3.837 است به این معنی که اگر مقدار متغیر عامل را در نظر نگرفته باشیم، با افزایش هر واحد به درآمد بعد از آزمایش مقدار 3.837 واحد درآمد افراد افزایش می‌یابد. ولی اختلاف در درآمد کسانی که روش prog=0 را انتخاب کرده‌اند نسبت به افرادی که روش prog=1 را به کار گرفته‌اند مقدار 3.640 واحد کمتر است، به شرطی که اثر درآمد قبل از طرح یعنی incbef را کنار گذاشته باشیم. بنابراین فرض صفر که بی‌اثر بودن روش درآمدزیایی است را رد می‌کنیم. مقدار اثر برای هر یک از این متغیرها نیز در ستون Partial Eta Squared در مدل رگرسیونی دیده می‌شود. برای مشاهده نحوه محاسبه مقدار اثر Eta بهتر است مطلب تحلیل واریانس دو طرفه در پایتون — راهنمای گام به گام را مطالعه کنید.

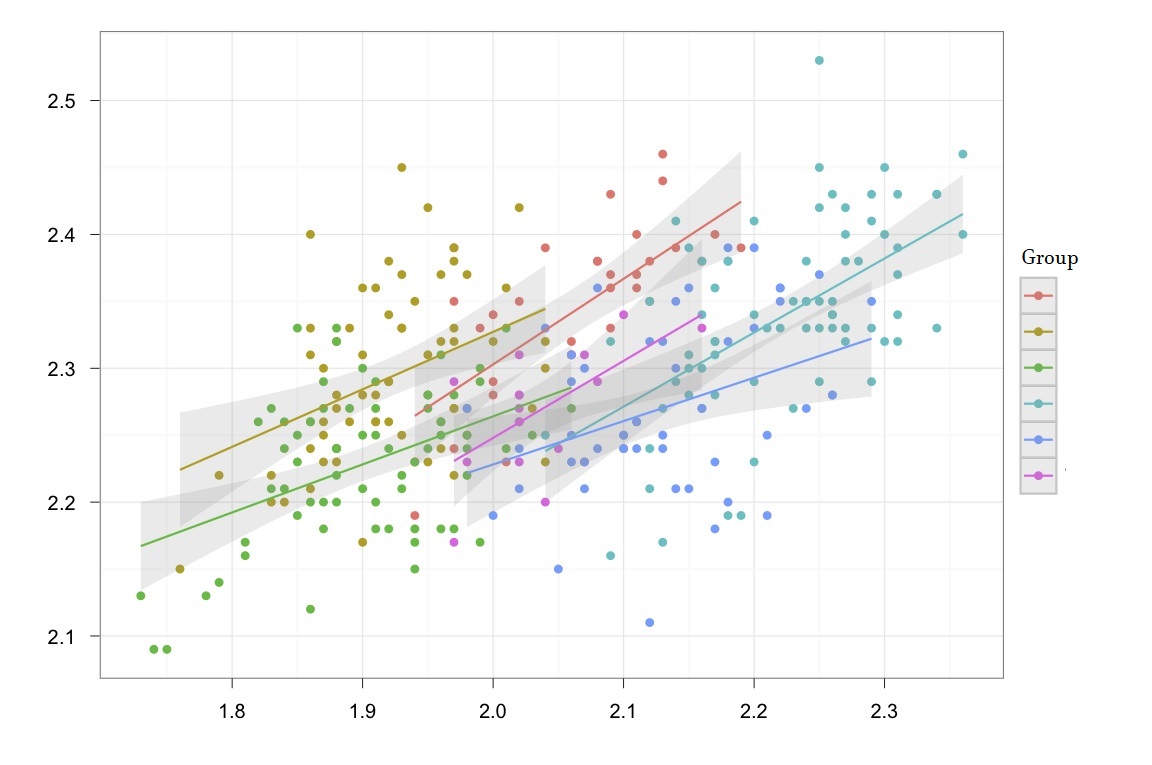
در انتها نیز نمودارهای درخواستی به نام Spread vs Level ترسیم شده است که در آن‌ها تغییرات میانگین در محور افقی و تغییرات پراکندگی در محور عمودی دیده می‌شود. انتظار داریم با فرض برابری واریانس‌ها در بین گروه‌های تولید شده توسط متغیر عامل، بتوان به شکل ذهنی خطی بین دو نقطه ترسیم کنیم که شیب آن صفر بوده یا شیب بسیار ملایمی داشته باشد ولی متاسفانه در این نمودارها چنین نیست. البته این امر به این علت رخ داده است که نسبت واحدها روی محور افقی و عمودی به صورت یکسان در نمودار ظاهر نشده است. روی محور افقی مقیاس برحسب ۱ واحد طولی است ولی در محور عمودی این تغییرات بر حسب 0.1 واحد است. بنابراین تغییرات روی محور افقی باید ۱۰ برابر تغییرات روی محور عمودی نشان داده و در نظر گرفته شود.

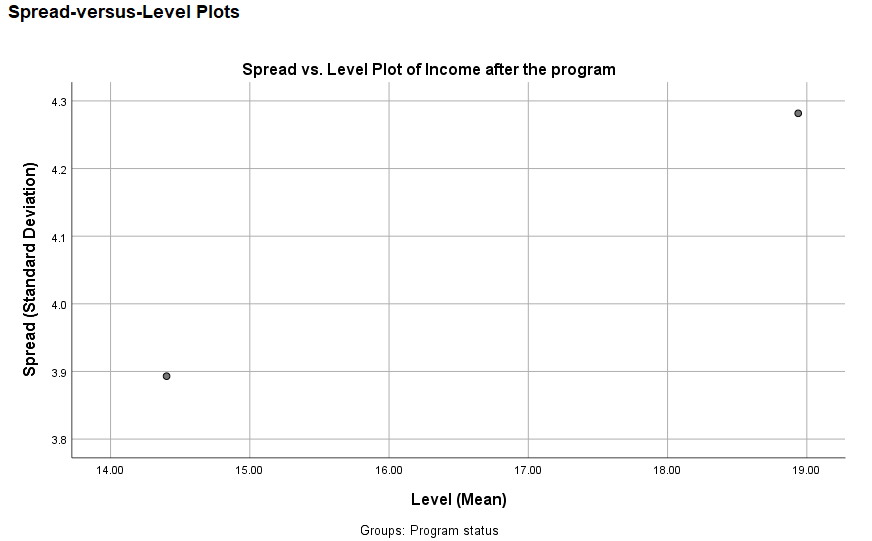
هر چند به نظر می‌رسد که خط فرضی ما شیب زیادی دارد ولی باید به این موضوع نیز توجه داشت که تغییر در میانگین برابر با حدود 4.5 واحد است در حالیکه تغییر در انحراف استانداردها فقط حدود 0.4 واحد است. پس به نظر می‌رسد تغییرات زیادی روی انحراف معیار وجود ندارد. در نمودار دوم (که البته در اینجا ترسیم نشده) همین مقایسه بین میانگین‌ها و واریانس صورت گرفته است. شکل و شیب نمودار دوم نیز دقیقا شبیه نمودار اول خواهد بود.

جمع‌بندی و بررسی نتایج

در این نوشتار به بررسی تحلیل کوواریانس (چند متغیره) و مقایسه آن با تحلیل واریانس یک طرفه پرداختیم. همچنین نحوه انجام محاسبات مربوط را هم با استفاده از مثالی در SPSS‌ پی گرفتیم. مشخص شد که وجود یک متغیر مداخله‌گر، می‌تواند در مدل تحلیل واریانس، یک رابطه رگرسیونی را اضافه کند. به همین علت، چنین تحلیلی را به صورت تحلیل کوواریانس می‌نامند تا نشان دهند که متغیر وابسته با متغیر مزاحم یا مداخله‌گر، در مدل به صورت یک رابطه خطی حضور دارد. البته در این میان روش‌هایی ارزیابی صحت مدل را نیز مرور و مورد بررسی قرار دادیم.

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری بیشتر در این زمینه هستید، آموزش‌ها و نوشتارهای زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های برنامه‌نویسی پایتون Python
• آموزش تکمیلی برنامه‌نویسی R و نرم‌افزار RStudio
• آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی
• تحلیل واریانس (Anova) — مفاهیم و کاربردها
• تحلیل واریانس یک طرفه در پایتون — راهنمای گام به گام