برنامه پیدا کردن ریشه های تابع با روش نابجایی – راهنمای کاربردی

در این مطلب، روش نوشتن برنامه پیدا کردن ریشه های تابع با روش نابجایی بیان و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و «پی‌اچ پی» (PHP) انجام شده است.

برنامه پیدا کردن ریشه های تابع با روش نابجایی

تابعf(x) ‎ روی x و دو عدد a و b داده شده است؛ به طوری که، f(a)*f(b) < 0 وf(x) ‎ در [a, b] پیوسته است. در اینجا، f(x)‎ نشانگر یک معادله جبری یا غیر جبری است. هدف، پیدا کردن ریشه تابع در بازه [a, b] (یا پیدا کردن مقدار x به طوری که f(x)‎ برابر با ۰ باشد) است. مثال زیر در این راستا قابل توجه است.

ورودی: یک تابع از x، برای مثال x³ – x² + 2 و دو مقدار a = -200 و b = 300 به طوری است که f(a)*f(b) < 0، یعنی f(a)‎ و f(b)‎ دارای علامت‌های مخالف یکدیگر هستند.

خروجی: مقدار ریشه برابر است با: 1.00‎- یا هر مقدار دیگر نزدیک به ریشه.

توصیه می‌شود که پیش از مطالعه این نوشتار، مطلب «برنامه پیدا کردن ریشه های تابع با روش دو بخشی — راهنمای کاربردی» مطالعه شود. در این مطلب، روش نابجایی (Method Of False Position | Regula Falsi) مورد مطالعه قرار خواهد گرفت.

شباهت‌های روش نابجایی با روش دوبخشی

روش نابجایی، شباهت‌هایی با «روش دوبخشی» (Bisection Method) دارد که در ادامه مورد بررسی قرار گرفته‌اند.

• فرضیات مشابه: این روش نیز فرض می‌کند که تابع در بازه [a, b] پیوسته است و دو عدد a و b داده شده‌اند، به طوری که f(a) * f(b) < 0.
• همیشه همگرا می‌شود: این روش نیز مانند روش دوبخشی، همیشه همگرا می‌شود؛ معمولا همگرایی در این روش، سریع‌تر از روش دوبخشی به  وقوع می‌پیوندد. اما گاهی نیز همگرایی خیلی کندتر از روش دو بخشی اتفاق می‌افتد.

تفاوت‌های روش نابجایی با روش دو بخشی

این دو روش در این رویکرد با یکدیگر متفاوت هستند که در روش نابجایی، وتری ترسیم می‌شود که دو نقطه a, f(a)]‎] و [b, f(b)‎] را به یکدیگر متصل می‌کند. سپس، نقطه‌ای در نظر گرفته می‌شود که وتر، با محور x برخورد می‌کند و این نقطه، c نامیده می‌شود.

گام‌های روش نابجایی

۱. معادله خطی که دو نقطه را به یکدیگر متصل می‌کند، نوشته می‌شود.

y – f(a) =  ( (f(b)-f(a))/(b-a) )*(x-a)

اکنون، باید نقطه‌ای پیدا شود که با x برخورد داشته باشد، بنابراین y = 0 قرار داده می‌شود.

x = a - (f(a)/(f(b)-f(a))) * (b-a)
x = (a*f(b) - b*f(a)) / (f(b)-f(a))

این، در واقع c است که در آن، c = x است.

۲. اگر f(c) == 0، پس c ریشه تابع است.

۳. در غیر این صورت، اگر f(c) != 0:

    ۱. اگر f(a)*f(c) < 0، پس ریشه بین a و c قرار دارد. بنابراین، تکرار برای a و c انجام می‌شود.

    ۲. در غیر این صورت، اگر f(b)*f(c) < 0، پس ریشه بین b و c قرار دارد. بنابراین، تکرار برای b و c انجام می‌شود.

     ۳. در غیر این صورت، تابع داده شده از یکی از فرضیات تبعیت نمی‌کند.

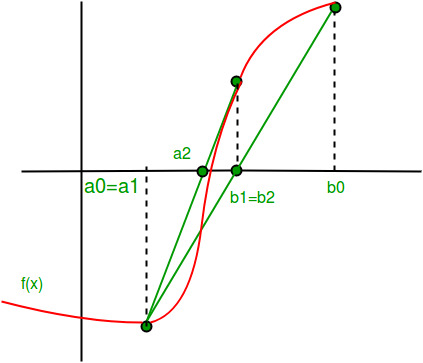
از آنجا که ممکن است ریشه، یک نقطه شناور باشد و در بدترین حالت به آرامی همگرا شود، تکرار به تعداد دفعات بسیار زیادی انجام می‌شود و همین موجب می‌شود تا پاسخ به ریشه نزدیک‌تر شود. در ادامه، پیاده‌سازی این روش در زبان‌های برنامه‌نویسی گوناگون انجام شده است.

برنامه پیدا کردن ریشه های تابع با روش نابجایی در ++C

فیلم آموزش ساختمان داده ها و پیاده سازی در سی پلاس پلاس C++‎ در فرادرس

کلیک کنید

برنامه پیدا کردن ریشه های تابع با روش نابجایی در جاوا

برنامه پیدا کردن ریشه های تابع با روش نابجایی در پایتون

فیلم آموزش برنامه نویسی پایتون Python – مقدماتی + گواهینامه در فرادرس

کلیک کنید

برنامه پیدا کردن ریشه های تابع با روش نابجایی در #C

فیلم آموزش تابع در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

خروجی قطعه کدهای بالا به صورت زیر است.

The value of root is : -1

این روش همیشه همگرا می‌شود و همگرایی در آن، معمولا سریع‌تر از روش دو بخشی اتفاق می‌افتد. اما در بدترین حالت ممکن است بسیار کند باشد.

فیلم مجموعه آموزش برنامه نویسی – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• متن کاوی (Text Mining) — به زبان ساده

^^