روش دو بخشی – به زبان ساده (+ دانلود فیلم آموزش گام به گام)

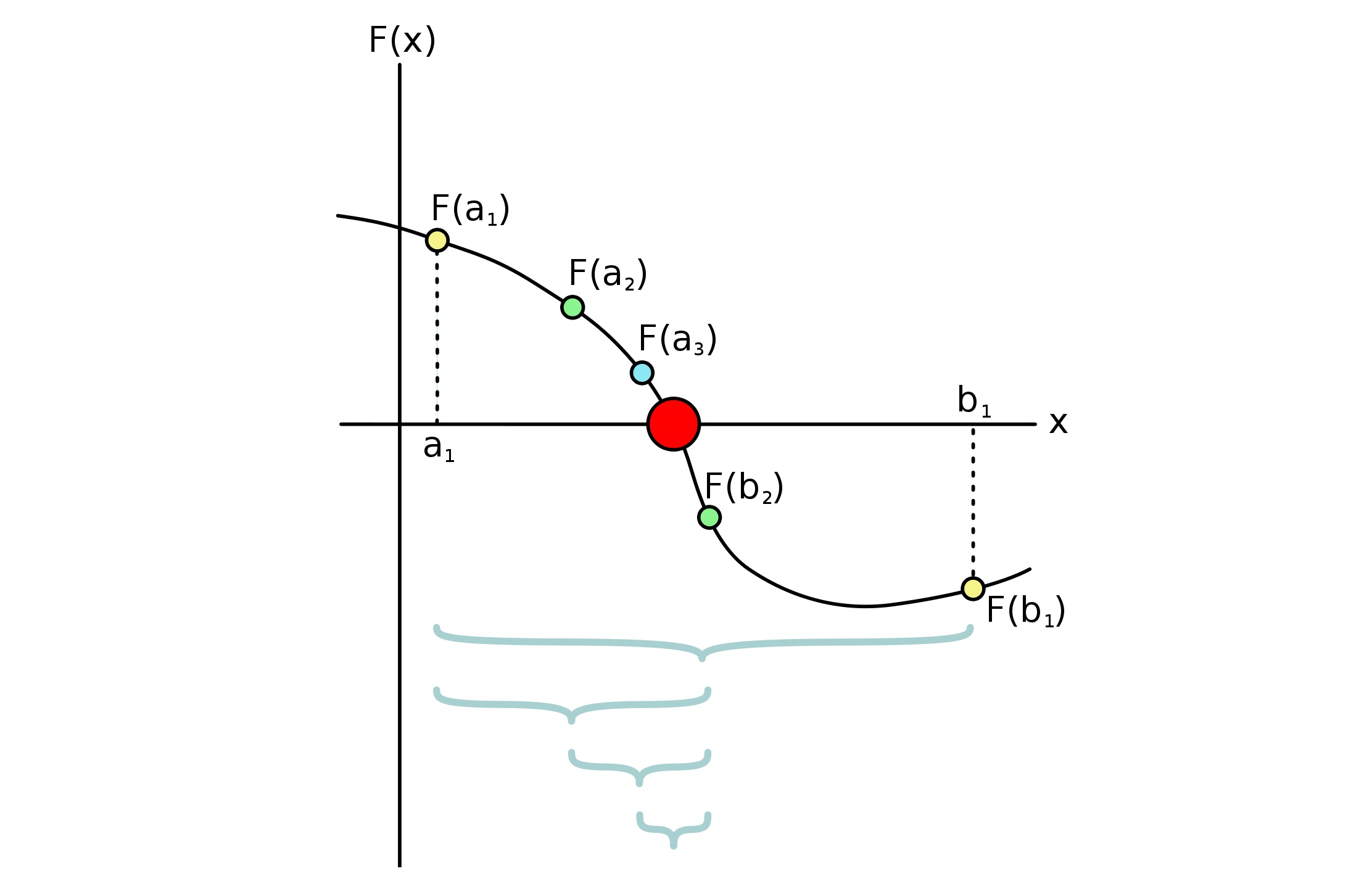
ساده‌ترین الگوریتم یافتن ریشه معادلات روش دو بخشی یا تنصیف (Bisection Method) است. این الگوریتم را می‌توان بر هر تابع پیوسته $$f ( x )$$ در بازه $$[a,b]$$ اعمال کرد که علامت مقدار تابع $$f ( x )$$ از $$a$$ تا $$b$$ تغییر می‌کند. فرایند روش دو بخشی ساده است: بازه به دو قسمت تقسیم می‌کنیم و یک جواب باید در یک زیربازه وجود داشته باشد که در آن، علامت $$f(x)$$ تغییر می‌کند. روند مذکور را تکرار می‌کنیم.

الگوریتم روش دو بخشی

فرایند روش دو بخشی به صورت زیر است:

1. بازه شروع $$[a_0,b_0]$$ را انتخاب کنید، به گونه‌ای که $$f(a_0)f(b_0) < 0$$.
2. نقطه میانی $$f(m_0)$$ که $$m_0 = (a_0+b_0)/2$$ را محاسبه کنید.

1. زیربازه $$[a_1,b_1]$$ را تعیین کنید:
   1. اگر $$f(a_0)f(m_0) < 0$$، آنگاه $$[a_1,b_1]$$ به عنوان بازه بعدی در نظر گرفته می‌شود که در آن، $$a_1=a_0$$ و $$b_1=m_0$$.
   2. اگر $$f(b_0)f(m_0) < 0$$، آنگاه $$[a_1,b_1]$$ به عنوان بازه بعدی در نظر گرفته می‌شود که در آن، $$a_1=m_0$$ و $$b_1=b_0$$.
2. مراحل ۲ و ۳ را تا زمانی که طول بازه $$[a_N,b_N]$$ به یک مقدار از پیش تعیین شده برسد، تکرار کنید.
3. نقطه میانی $$m_N=(a_N+b_N)/2$$ را محاسبه کنید.

طبق قضیه مقدار میانی، یک جواب برای معادله $$f(x)=0$$ در بازه $$[a,b]$$ تضمین شده است که $$f ( x)$$ در بازه $$[a,b]$$ پیوسته بوده و $$f(a)f(b) < 0$$. به عبارت دیگر، علامت تابع در بازه مذکور تغییر کرده و در نتیجه، باید در نقطه (یا نقاطی) درون بازه برابر با صفر شود.

خطای مطلق روش دو بخشی

روش دو بخشی (عموماً) رویکردی برای به دست آوردن جواب دقیق معادله $$f ( x ) = 0$$ به دست نمی‌دهد. البته، می‌توانیم مقدار خطای مطلق را در تقریب تخمین بزنیم.

قضیه

فرض کنید $$f ( x)$$ تابعی پیوسته در بازه $$[a,b]$$ باشد به گونه‌ای که $$f(a)f(b) < 0$$. اگر بعد از $$N$$ تکرار روش دو بخشی، $$x _ N$$ نقطه میانی در $$N$$اُمین زیربازه $$[a_N,b_N]$$ باشد:

$$\large x_N = \frac{a_N + b_N}{2}$$

آنگاه جواب دقیق $$x_{\mathrm{true}}$$ معادله $$f(x)=0$$ در زیربازه $$[a_N,b_N]$$ وجود خواهد داشت و مقدار خطای مطلق برابر است با:

$$\large \left| \ x _ { \text {true} } - x _ N \, \right | \leq \frac { b - a } { 2 ^ { N + 1 } }$$

می‌توانیم محدوده خطا را برای مشاهده حداقل تکرار لازم برای تضمین کمتر بودن خطای مطلق از مقدار از پیش تعیین شده $$\epsilon$$ بازنویسی کنیم:

$$\large \begin {align} \frac { b - a } { 2 ^ { N + 1 } } & < \epsilon \\ \frac { b - a } { \epsilon } & < 2 ^ { N + 1 } \\ \ln \left ( \frac { b - a } { \epsilon } \right ) & < ( N + 1 ) \ln ( 2 ) \\ \frac { \ln \left ( \frac { b - a } { \epsilon } \right ) } { \ln ( 2 ) } - 1 & < N \end {align}$$

پیاده‌سازی در پایتون

تابعی می‌نویسیم و نام آن را "bisection" قرار می‌دهیم. این تابع چهار ورودی "b" ،"a" ،"f" و "N" دارد و خروجی آن، حل معادله $$f ( x ) =0$$ با $$N$$ بار تکرار روش دو بخشی است. اگر در هر نقطه از تکرار داشته باشیم: $$f(a_n)f(b_n) \geq 0$$ (به دلیل بازه اولیه نامناسب یا گرد کردن خطا در محاسبات)، آنگاه در خروجی برنامه، عبارت "Bisection method fails." چاپ می‌شود و خروجی "None" خواهد بود.

برنامه پایتون مربوط به تابع مذکور به صورت زیر است.

برای مثال، پارامترهای ورودی تابع را $$f(x)=x^2 - x - 1$$ و $$N=25$$ تکرار در بازه $$[1,2]$$ در نظر می‌گیریم و می‌خواهیم نسبت طلایی را تقریب بزنیم:

$$\large \phi = \frac { 1 + \sqrt { 5 } } { 2 }$$

نسبت طلایی $$\phi$$، ریشه چندجمله‌ای درجه دوم $$x^2 - x - 1 = 0$$ است.

1.618033990263939

همچنین تضمین می‌شود که مقدار خطای مطلق کمتر از $$(2 - 1)/(2^{26})$$ باشد:

1.4901161193847656e-08

بررسی می‌کنیم که مقدار خطای مطلق کمتر از محدوده خطا باشد:‌

True

پیاده‌سازی در متلب

روش دو بخشی را می‌توان به سادگی در متلب نیز پیاده‌سازی کرد.

فیلم آموزش محاسبات عددی با متلب MATLAB در فرادرس

کلیک کنید

برای مثال، کد متلب روش دو بخشی برای یافتن ریشه $$p(x)=x^3-x-2$$ در بازه $$[0,2]$$ به صورت زیر است:

خروجی این حاصل از اجرای کد بالا به صورت زیر خواهد بود:

n = 1, x = 1, f(x) = -2
n = 2, x = 1.5, f(x) = -0.125
n = 3, x = 1.75, f(x) = 1.6094
n = 4, x = 1.625, f(x) = 0.66602
n = 5, x = 1.5625, f(x) = 0.2522
n = 6, x = 1.5313, f(x) = 0.059113
n = 7, x = 1.5156, f(x) = -0.034054
n = 8, x = 1.5234, f(x) = 0.01225
n = 9, x = 1.5195, f(x) = -0.010971
n = 10, x = 1.5215, f(x) = 0.00062218
n = 11, x = 1.5205, f(x) = -0.0051789
n = 12, x = 1.521, f(x) = -0.0022794
n = 13, x = 1.5212, f(x) = -0.00082891
n = 14, x = 1.5214, f(x) = -0.00010343
n = 15, x = 1.5214, f(x) = 0.00025935
n = 16, x = 1.5214, f(x) = 7.7956e-05
n = 17, x = 1.5214, f(x) = -1.2739e-05
n = 18, x = 1.5214, f(x) = 3.2608e-05
n = 19, x = 1.5214, f(x) = 9.9343e-06
n = 20, x = 1.5214, f(x) = -1.4026e-06

به طور مشابه، کد زیر و نتیجه آن مربوط به روش دو بخشی برای یافتن ریشه معادله $$f ( x ) =0.2\cosh (x) + \cos ( x ) - 3$$ در بازه $$[0,6]$$ است:

نتیجه:

n = 1, x = 3, f(x) = -1.9765
n = 2, x = 4.5, f(x) = 5.792
n = 3, x = 3.75, f(x) = 0.4339
n = 4, x = 3.375, f(x) = -1.047
n = 5, x = 3.5625, f(x) = -0.38476
n = 6, x = 3.6563, f(x) = 0.0037101
n = 7, x = 3.6094, f(x) = -0.19557
n = 8, x = 3.6328, f(x) = -0.097211
n = 9, x = 3.6445, f(x) = -0.047073
n = 10, x = 3.6504, f(x) = -0.021763
n = 11, x = 3.6533, f(x) = -0.0090467
n = 12, x = 3.6548, f(x) = -0.0026734
n = 13, x = 3.6555, f(x) = 0.00051706
n = 14, x = 3.6552, f(x) = -0.0010785
n = 15, x = 3.6553, f(x) = -0.0002808
n = 16, x = 3.6554, f(x) = 0.00011811
n = 17, x = 3.6554, f(x) = -8.1348e-05
n = 18, x = 3.6554, f(x) = 1.838e-05
n = 19, x = 3.6554, f(x) = -3.1484e-05
n = 20, x = 3.6554, f(x) = -6.5521e-06

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• روش نیوتن — به زبان ساده
• دستگاه معادلات خطی — به زبان ساده
• جذر یا محاسبه ریشه دوم عدد — به زبان ساده

^^