برنامه پیدا کردن ریشه های تابع با روش دو بخشی — راهنمای کاربردی

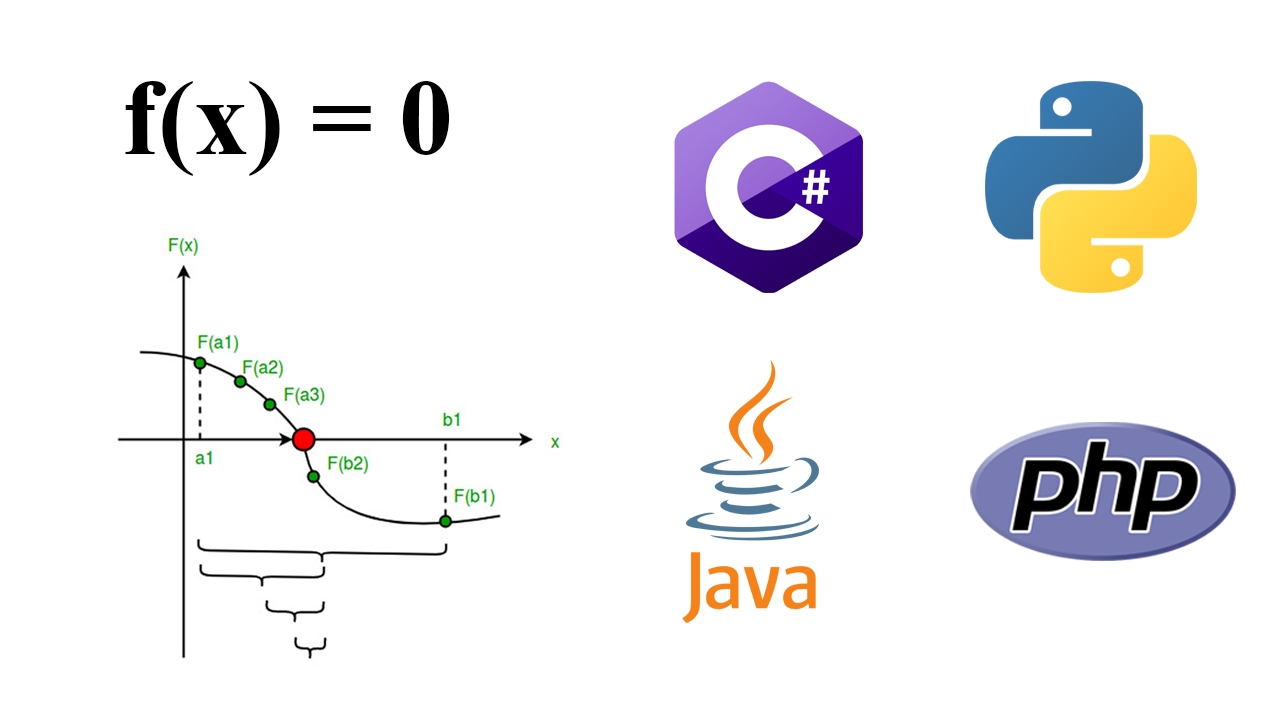
در این مطلب، روش نوشتن برنامه پیدا کردن ریشه های تابع با روش دو بخشی بیان و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و «پی‌اچ پی» (PHP) انجام شده است. تابع f(x)‎ روی عدد ممیز شناور x و همچنین، دو عدد a و b داده شده است؛ به طوری که f(a)*f(b) < 0‎ و f(x)‎ در [a, b] پیوسته است. در اینجا، f(x)‎ نشانگر یک معادله جبری یا غیر جبری است. هدف، پیدا کردن ریشه در بازه [a, b] (یا پیدا کردن مقداری از x به طوری است که f(x) = 0) است. مثال زیر،‌ به درک بهتر این مطلب کمک می‌کند.

ورودی: تابعی از x، مثلا x3 - x2 + 2 و دو مقدار a = -200 و b = 300 به گونه‌ای که f(a)*f(b) < 0 و f(a)‎ و f(b)‎ علامت‌های مخالف هم دارند.

خروجی: The value of root is : -1.0025 (یا هر مقدار ممکن دیگری با انحراف پذیرفته شده از ریشه).

ممکن است این پرسش برای برخی از افراد مطرح شود که توابع جبری و غیر جبری چه هستند؟ توابع جبری، توابعی محسوب می‌شوند که می‌توان آن‌ها را به صورت چند جمله‌ایی‌هایی مانند f(x) = a₁x³ + a₂x² +‎ ….. + e نشان داد که در آن‌ها، aa₁, a₂, …‎ ثابت‌ها و x یک متغیر است. به عنوان مثال‌هایی از توابع غیر جبری، می‌توان به توابعی به صورت f(x) = sin(x)*x – 3 یا f(x) = e^x + x² یا f(x) = ln(x) + x ….‎ اشاره کرد.

روش دو بخشی چیست؟

این روش که آن را روش «تنصیف»، «نصف شدن فاصله» (Interval Halving Method) یا «دو بخشی» (Bisection Method) نیز می‌نامند، یک روش «جستجوی دودویی» (Binary Search Method) یا روش دوگانگی (Dichotomy Method) است. از این روش برای پیدا کردن ریشه یک معادله در بازه داده شده استفاده می‌شود. در واقع روش دو بخشی برای پیدا کردن مقدار x برای f(x) = 0 مورد استفاده قرار می‌گیرد.

فیلم آموزش رایگان اصول و مبانی برنامه نویسی در فرادرس

کلیک کنید

این روش بر اساس «قضیه مقدار میانی» (The Intermediate Value Theorem) است. قضیه مقدار میانی بیان می‌کند که اگر f(x) ‎ یک تابع پیوسته باشد و دو عدد حقیقی a و b به طوری که f(a)*f(b) 0 و f(b) < 0 وجود داشته باشند، تضمین می‌شود که حداقل یک ریشه بین آن‌ها وجود داشته باشد.

فرضیات

• f(x)‎ یک تابع پیوسته در بازه [a, b] است.
• f(a) * f(b) < 0

گام‌ها

1. هدف پیدا کردن نقطه میانی c= (a + b)/2 است.
2. اگر f(c) == 0، بنابراین c ریشه و پاسخ مسئله است.
3. در غیر این صورت، f(c) != 0
   1. اگر مقدار f(a)*f(c) < 0، بنابراین ریشه بین a و c خواهد بود. بنابراین، برای a و c نیز تکرار می‌شود.
   2. در غیر این صورت، اگر f(b)*f(c) < 0، ریشه بین b و c قرار دارد. بنابراین تکرار برای b و c انجام می‌شود.
   3. در غیر این صورت، تابع داده شده هیچ یک از مفروضات را دنبال نمی‌کند.
   4. از آنجا که ریشه ممکن است یک عدد ممیز شناور باشد، گام‌های بالا تا هنگامی که تفاوت بین a و b کمتر از یک مقدار (یک مقدار بسیار کوچک) باشد، تکرار می‌شوند.

در ادامه، پیاده‌سازی گام‌های بالا در زبان‌های برنامه‌نویسی گوناگون انجام شده است.

برنامه پیدا کردن ریشه های تابع با روش دو بخشی در ++C

فیلم آموزش ساختمان داده ها و پیاده سازی در سی پلاس پلاس C++‎ در فرادرس

کلیک کنید

// C++ program for implementation of Bisection Method for 
// solving equations 
#include<bits/stdc++.h> 
using namespace std; 
#define EPSILON 0.01 
  
// An example function whose solution is determined using 
// Bisection Method. The function is x^3 - x^2  + 2 
double func(double x) 
{ 
    return x*x*x - x*x + 2; 
} 
  
// Prints root of func(x) with error of EPSILON 
void bisection(double a, double b) 
{ 
    if (func(a) * func(b) >= 0) 
    { 
        cout << "You have not assumed right a and b\n"; 
        return; 
    } 
  
    double c = a; 
    while ((b-a) >= EPSILON) 
    { 
        // Find middle point 
        c = (a+b)/2; 
  
        // Check if middle point is root 
        if (func(c) == 0.0) 
            break; 
  
        // Decide the side to repeat the steps 
        else if (func(c)*func(a) < 0) 
            b = c; 
        else
            a = c; 
    } 
    cout << "The value of root is : " << c; 
} 
  
// Driver program to test above function 
int main() 
{ 
    // Initial values assumed 
    double a =-200, b = 300; 
    bisection(a, b); 
    return 0; 
}

برنامه پیدا کردن ریشه های تابع با روش دو بخشی در جاوا

فیلم آموزش مبانی برنامه نویسی – الگوریتم و فلوچارت با رویکرد حل مساله در فرادرس

کلیک کنید

// Java program for implementation of Bisection Method  
// for solving equations 
class GFG{ 
    static final float EPSILON = (float)0.01; 
  
    // An example function whose solution is determined using 
    // Bisection Method. The function is x^3 - x^2  + 2 
    static double func(double x) 
    { 
        return x*x*x - x*x + 2; 
    } 
  
    // Prints root of func(x) with error of EPSILON 
    static void bisection(double a, double b) 
    { 
        if (func(a) * func(b) >= 0) 
        { 
            System.out.println("You have not assumed"
                        + " right a and b"); 
            return; 
        } 
  
        double c = a; 
        while ((b-a) >= EPSILON) 
        { 
            // Find middle point 
            c = (a+b)/2; 
  
            // Check if middle point is root 
            if (func(c) == 0.0) 
                break; 
  
            // Decide the side to repeat the steps 
            else if (func(c)*func(a) < 0) 
                b = c; 
            else
                a = c; 
        } 
                //prints value of c upto 4 decimal places 
        System.out.printf("The value of root is : %.4f"
                        ,c); 
    } 
  
    // Driver program to test above function 
    public static void main(String[] args) 
    { 
        // Initial values assumed 
        double a =-200, b = 300; 
        bisection(a, b); 
    } 
    // This code is contributed by Nirmal Patel 
}

برنامه پیدا کردن ریشه های تابع با روش دو بخشی در پایتون

فیلم آموزش برنامه نویسی پایتون Python – مقدماتی در فرادرس

کلیک کنید

# Python program for implementation 
# of Bisection Method for 
# solving equations 
  
   
# An example function whose 
# solution is determined using 
# Bisection Method. 
# The function is x^3 - x^2  + 2 
def func(x): 
    return x*x*x - x*x + 2
   
# Prints root of func(x) 
# with error of EPSILON 
def bisection(a,b): 
  
    if (func(a) * func(b) >= 0): 
        print("You have not assumed right a and b\n") 
        return
   
    c = a 
    while ((b-a) >= 0.01): 
  
        # Find middle point 
        c = (a+b)/2
   
        # Check if middle point is root 
        if (func(c) == 0.0): 
            break
   
        # Decide the side to repeat the steps 
        if (func(c)*func(a) < 0): 
            b = c 
        else: 
            a = c 
              
    print("The value of root is : ","%.4f"%c) 
      
# Driver code 
# Initial values assumed 
a =-200
b = 300
bisection(a, b) 
  
# This code is contributed 
# by Anant Agarwal.

برنامه پیدا کردن ریشه های تابع با روش دو بخشی در #C

// C# program for implementation  
// of Bisection Method for  
// solving equations 
using System; 
  
class GFG 
{ 
static float EPSILON = (float)0.01; 
  
// An example function whose  
// solution is determined using 
// Bisection Method. The function 
// is x^3 - x^2 + 2 
static double func(double x) 
{ 
    return x * x * x -  
           x * x + 2; 
} 
  
// Prints root of func(x)  
// with error of EPSILON 
static void bisection(double a,  
                      double b) 
{ 
    if (func(a) * func(b) >= 0) 
    { 
        Console.WriteLine("You have not assumed" +  
                                " right a and b"); 
        return; 
    } 
  
    double c = a; 
    while ((b - a) >= EPSILON) 
    { 
        // Find middle point 
        c = (a + b) / 2; 
  
        // Check if middle  
        // point is root 
        if (func(c) == 0.0) 
            break; 
  
        // Decide the side  
        // to repeat the steps 
        else if (func(c) * func(a) < 0) 
            b = c; 
        else
            a = c; 
    } 
      
    // prints value of c  
    // upto 4 decimal places 
    Console.WriteLine("The value of " +  
                      "root is : "+ c); 
} 
  
// Driver Code 
static public void Main () 
{ 
    // Initial values assumed 
    double a = -200, b = 300; 
    bisection(a, b); 
} 
} 
  
// This code is contributed by ajit 

برنامه پیدا کردن ریشه های تابع با روش دو بخشی در PHP

فیلم آموزش تابع در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

<?php 
// PHP program for implementation  
// of Bisection Method for solving 
// equations 
$EPSILON = 0.01; 
  
// An example function whose  
// solution is determined  
// using Bisection Method.  
// The function is x^3 - x^2 + 2 
function func($x) 
{ 
    return $x * $x * $x -  
           $x * $x + 2; 
} 
  
// Prints root of func(x) 
// with error of EPSILON 
function bisection($a, $b) 
{ 
    global $EPSILON; 
    if (func($a) *  
        func($b) >= 0) 
    { 
        echo "You have not assumed " .  
                 "right a and b","\n"; 
        return; 
    } 
  
    $c = $a; 
    while (($b - $a) >= $EPSILON) 
    { 
        // Find middle point 
        $c = ($a + $b) / 2; 
  
        // Check if middle  
        // point is root 
        if (func($c) == 0.0) 
            break; 
  
        // Decide the side to 
        // repeat the steps 
        else if (func($c) * func($a) < 0) 
            $b = $c; 
        else
            $a = $c; 
    } 
    echo "The value of root is : " , $c; 
} 
  
// Driver Code 
  
// Initial values assumed 
$a =-200; 
$b = 300; 
bisection($a, $b); 
  
// This code is contributed by ajit 
?>

خروجی قطعه کدهای بالا، به صورت زیر است.

The value of root is : -1.0025

پیچیدگی زمانی این روش بستگی به مقادیر مفروض و خود تابع دارد.

مزایا و معایب روش دوبخشی

مزیت روش دوبخشی در آن است که این روش تضمین می‌کند که همگرا شود. عیب اصلی این روش آن است که نمی‌تواند چندین ریشه را پیدا کند. به طور کلی، روش دو بخشی برای به دست آوردن یک تخمین خام از راهکار، مورد استفاده قرار می‌گیرد. روش‌هایی که سریع‌تر همگرا می‌شوند، برای پیدا کردن جواب‌ها مورد استفاده قرار می‌گیرند.

فیلم مجموعه آموزش برنامه‌نویسی در فرادرس

کلیک کنید

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• متن کاوی (Text Mining) — به زبان ساده

^^