طول قوس منحنی (کاربرد انتگرال) — به زبان ساده (+ دانلود فیلم آموزش رایگان)

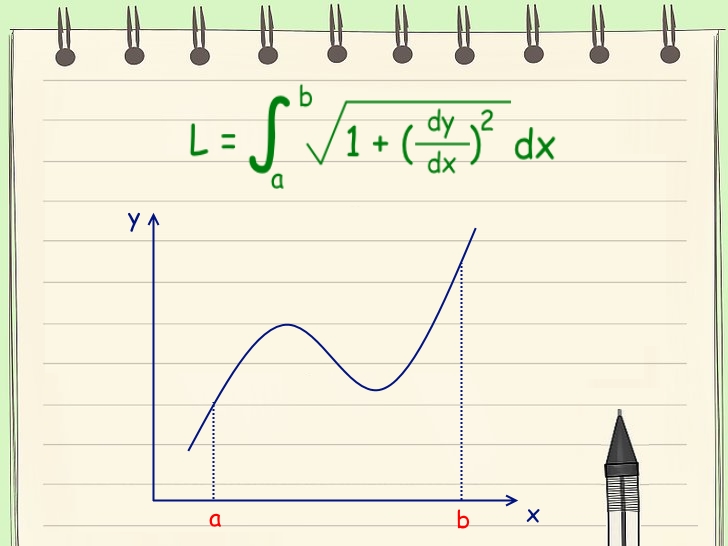
در مباحث قبلی وبلاگ فرادرس، انتگرال توابع مختلف به صورت دقیق مورد بررسی قرار گرفت. همانطور که بیان شد یکی از کاربردهای انتگرال، محاسبه طول قوس منحنی و طول کمان است و این مفهوم کاربرد زیادی در ریاضیات و هندسه دارد. در واقع در صورتی که رابطه یک منحنی و تابع موجود باشد، طول قوس این منحنی در هر بازه به کمک انتگرال‌گیری قابل محاسبه است.

این مطلب به صورت دقیق به بررسی روابط مختلف مربوط به طول قوس منحنی می‌پردازد و با استفاده از چند مثال، شیوه استفاده از این روابط را مورد ارزیابی قرار می‌دهد.

طول قوس منحنی

همانطور که اشاره شد، در این بخش، ما به دنبال یافتن راهی برای محاسبه طول قوس منحنی یا طول منحنی یک تابع در یک بازه مشخص هستیم. در واقع این مطلب به دنبال یافتن طول تابع پیوسته $$ { { y } = { f } \left ( { x } \right ) } $$ در بازه $$ { \left [ { a , b } \right ] } $$ است. نکته دیگر این است که برای محاسبه طول قوس منحنی، باید فرض کنیم که مشتق تابع نیز در محدوده $$ { \left [ { a , b } \right ] } $$ به صورت یک تابع پیوسته قرار دارد.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

توجه کنید که در این قسمت در ابتدا ما باید طول قوس منحنی را تخمین بزنیم. این کار را با تقسیم کردن آن به $$ { n } $$ زیر بازه مساوی انجام می‌دهیم. این موضوع در شکل زیر به تصویر کشیده شده است.

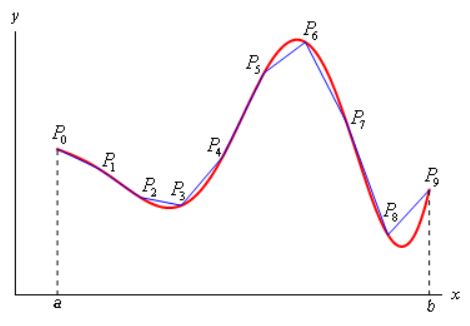
در این فرایند، عرض بازه‌های $$ { \Delta x } $$ با یکدیگر برابر هستند. در واقع این منحنی به کمک نقاط $$ { P _ i } $$ به $$ { n } $$ زیر بازه تقسیم شده است. در ادامه و همانطور که در شکل بالا نشان داده شده، شکل منحنی را به کمک یک سری خط‌های یکنواخت تخمین می‌زنیم. این خط‌های یکنواخت به کمک وصل شدن نقاط $$ { P _ i } $$ به یکدیگر به وجود آمده است. توجه کنید که شکل بالا با استفاده از ۹ نقطه رسم شده است و مقدار پارامتر $$ { n } $$ در روابط آن برابر با $$ { n = 9 } $$ در نظر گرفته می‌شود.

در ادامه، برای محاسبه طول کلی منحنی در بازه نشان داده شده، طول هرکدام از پاره‌خط‌ها یعنی $$ { \left | { { { P } _ { { i } - 1 } } \, \, { P _ { i } } } \right | } $$ را مورد ارزیابی قرار می‌دهیم. بنابراین طول کلی منحنی داده شده به شکل زیر بیان می‌شود.

$$ { \large L \approx \sum\limits_{a}^b { \left | { { { P } _ { i - 1 } } \, \, { P_i } } \right | } } $$

نکته بسیار مهم این است که با بزرگ شدن مقدار پارامتر $$ { n } $$، طول قوس منحنی این تابع به صورت دقیق‌تر محاسبه می‌شود. بنابراین پارامتر $$ { n } $$ را به سمت بینهایت میل می‌دهیم و رابطه بالا را به شکل حد در بینهایت و مطابق با رابطه زیر بیان می‌کنیم.

$$ { \large L = \mathop { \lim } \limits _ { n \to \infty } \sum \limits _ { i = 1 } ^ n { \left | { { P _ { i - 1 } } \, \, { P _ i } } \right | } } $$

در ادامه به صورت دقیق‌تری به دنبال یافتن طول هرکدام از این بخش‌ها هستیم. بنابراین در هرکدام از این بخش‌ها به دنبال یافتن $$ { \Delta { y _ i } = { y _ i } - { y _ { i - 1 } } = f \left ( { { x _ i } } \right ) - f \left ( { { x _ { i - 1 } } } \right ) } $$ هستیم. بر این اساس و همانطور که در مطلب «فاصله بین دو نقطه» بیان شد، طول این خط $$ { \left | { { { P } _ { { i } - 1 } } \, \, { P _ { i } } } \right | } $$ به شکل زیر محاسبه می‌شود.

$$ { \left | { { P _ { i - 1 } } \, \, { P _ i } } \right | = \sqrt { { { \left ( { { x _ i } - { x _ { i - 1 } } } \right ) } ^ 2 } + { { \left ( { { y _ i } - { y _ { i - 1 } } } \right ) } ^ 2 } } = \sqrt { \Delta { x ^ 2 } + \Delta y _ i ^ 2 } } $$

همانطور که در قضیه مقدار میانگین بیان شد، در هر بازه مانند $$ { \left [ { { { x } _ { { i } - 1 } } , { { x } _ i } } \right ] } $$، نقطه‌ای مانند $$ { x _ i ^ * } $$ وجود دارد که رابطه زیر در آن برقرار است.

$$ { \large \begin {align*} f \left ( { { x _ i } } \right ) - f \left ( { { x _ { i - 1 } } } \right ) & = f ^ \prime \left ( { x _ i ^ *} \right ) \left ( { { x _ i } - { x _ { i - 1 } } } \right ) \\ \end{align*} }$$

$$ { \large \begin {align*} \Delta { y _ i } = f ^ \prime \left ( { x _ i ^ * } \right ) \Delta x \end {align*} } $$

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

بنابراین رابطه طول خط $$ { \left | { { { P } _ { { i } - 1 } } \, \, { P _ { i } } } \right | } $$ را می‌توان به شکل زیر بازنویسی کرد.

$$ { \large \begin {align*} \left | { { P _ { i - 1 } } \, \, { P _ i } } \right | & = \sqrt { { { \left ( { { x _ i } - { x _ { i - 1 } } } \right ) } ^ 2 } + { { \left ( { { y _ i } - { y _ { i - 1 } } } \right ) } ^ 2 } } \\ & = \sqrt { \Delta { x ^ 2 } + { { \left [ { f ^ \prime \left ( { x _ i ^ * } \right ) } \right ] } ^ 2 } \Delta { x ^ 2 } } \\ & = \sqrt { 1 + { { \left [ { f ^ \prime \left ( { x _ i ^ * } \right ) } \right ] } ^ 2 } } \, \, \, \Delta x \end {align*} } $$

بنابراین طول دقیق قوس منحنی نشان داده شده را می‌توان به کمک رابطه زیر به دست آورد.

$$ { \large \begin {align*} L & = \mathop { \lim } \limits _ { n \to \infty } \sum \limits _ { i = 1 } ^ n { \left | { { P _ { i - 1 } } \, \, { P _ i } } \right | } \\ & = \mathop { \lim } \limits _ { n \to \infty } \sum \limits _ { i = 1 } ^ n { \sqrt { 1 + { { \left [ { f ^ \prime \left ( { x _ i ^ * } \right ) } \right ] } ^ 2 } } \, \, \, \Delta x } \end {align*} } $$

در ادامه به کمک تعریف انتگرال، طول قوس منحنی را می‌توان با استفاده از رابطه انتگرالی زیر محاسبه کرد.

$$ { \large L = \int _ { { \, a } } ^ { { \, b } } { { \sqrt { 1 + { { \left [ { f ^ \prime \left ( x \right ) } \right ] } ^ 2 } } \, d x } } } $$

البته شیوه نمایش رابطه فوق به شکل زیر، در کتب مختلف رایج‌تر است.

$$ { \large L = \int _ { { \, a } } ^ { { \, b } } { { \sqrt { 1 + { { \left ( { \frac { { d y } }{ { d x } } } \right ) } ^ 2 } } \, d x } } } $$

به صورت مشابه می‌توان بیان کرد که اگر رابطه ما به شکل $$ { x = h \left ( y \right ) } $$ و در بازه $$ { \left [ { c , d } \right ] } $$ موجود باشد، رابطه زیر را برای محاسبه طول قوس منحنی می‌توان بیان کرد.

$$ { \large L = \int _ { { \, c } } ^ { { \, d } } { { \sqrt { 1 + { { \left [ { h ^ \prime \left ( y \right ) } \right ] } ^ 2 } } \, d y } } = \int _ { { \, c } } ^ { { \, d } } { { \sqrt { 1 + { { \left ( { \frac { { d x } } { { d y } } } \right ) } ^ 2 } } \, d y } } } $$

همانطور که در دو رابطه بالا مشاهده می‌شود، عبارت زیر انتگرال در رابطه اول، مشتق y نسبت به x را بیان می‌کند و همچنین عبارت زیر انتگرال در رابطه دوم بیان کننده مشتق x نسبت به y است. بنابراین در این قسمت یک فرمول کلی برای محاسبه طول قوس منحنی ارائه خواهیم کرد. این فرمول به شکل زیر نشان داده می‌شود.

$$ { \large L = \int { { d s } } } $$

$$ { \large \begin {array} { * { 2 0 } { l } } \begin {align*} d s & = \sqrt { 1 + { { \left ( { \frac { { d y } } { { d x } } } \right ) } ^ 2 } } \, d x \, \hspace { 0.25 in } { \mbox { if } } y = f \left ( x \right ) , \, \, a \le x \le b \\ d s & = \sqrt { 1 + { { \left ( { \frac { { d x } } { { d y } } } \right ) } ^ 2 } } \, d y \, \hspace { 0.25 in } { \mbox { if } } x = h \left ( y \right ) , \, \, c \le y \le d \end {align*} \end {array} } $$

در ادامه به کمک چند مثال، شیوه استفاده از این فرمول‌ها را برای محاسبه طول قوس منحنی مورد ارزیابی و مطالعه قرار می‌دهیم.

مثال 1

طول قوس منحنی تابع $$ { y = \ln \left ( { \sec x } \right ) } $$ را در محدوده $$ { 0 \le x \le \frac { \pi } { 4 } } $$ محاسبه کنید.

فیلم آموزش ریاضی پایه دانشگاهی در فرادرس

کلیک کنید

در این حالت، باید از رابطه اول برای محاسبه طول قوس منحنی استفاده کنیم. دلیل این موضوع این است که ما رابطه $$ { y = f \left ( x \right ) } $$ را داریم. بنابراین ابتدا مشتق y نسبت به x را به شکل زیر محاسبه می‌کنیم.

$$ { \large \frac { { d y } } { { d x } } = \frac { { \sec x \tan x } } { { \sec x } } = \tan x} $$

$$ { { \large \left ( { \frac { { d y } } { { d x } } } \right ) ^ 2 } = { \tan ^ 2 } x } $$

حال رابطه به دست آمده را در فرمول $$ ds $$ برای محاسبه طول قوس منحنی قرار می‌دهیم.

$$ { \large d s = \sqrt { 1 + { { \left ( { \frac { { d y } } { { d x } } } \right ) } ^ 2 } } \, d x } $$

$$ { \large \begin {align*} \sqrt { 1 + { { \left ( { \frac { { d y } } { { d x } } } \right ) } ^ 2 } } & = \sqrt { 1 + { { \tan } ^ 2 } x } \\ & = \sqrt { { { \sec } ^ 2 } x } \\ & = \left | { \sec x } \right | \\ & = \sec x \end {align*} } $$

بنابراین طول قوس منحنی به شکل زیر محاسبه می‌شود.

$$ { \large \begin {align*} L & = \int _ { { \, 0 } } ^ { { \, \frac { \pi } { 4 } } } { { \sec x \, d x } } \\ & = \left. { \ln \left | { \sec x + \tan x } \right | } \right | _ 0 ^ { \frac { \pi }{ 4 } } \\ & = \ln \left ( { \sqrt 2 + 1 } \right ) \end {align*} } $$

مثال 2

طول قوس منحنی تابع $$ { x = \frac { 2 } { 3 } { \left ( { y - 1 } \right ) ^ { \frac { 3 } { 2 } } } } $$ را در محدوده $$ { 1 \le y \le 4 } $$ محاسبه کنید.

همانطور که مشاهده می‌شود، در این مثال، رابطه x بر حسب y داده شده، بنابراین یکی از روش‌ها این است که از رابطه طول قوس منحنی استفاده کنیم که برای تابع $$ { x = h \left ( y \right ) } $$ نوشته شده است. روش دیگر نیز این است که ابتدا رابطه مربوط به تابع $$ { y = f \left ( x \right ) } $$ را محاسبه کنیم و در نهایت با استفاده از رابطه مربوط به این تابع، طول قوس منحنی را مورد ارزیابی قرار دهیم. در این قسمت از روش اول استفاده می‌کنیم. بنابراین داریم:

$$ { \large \frac { { d x } } { { d y } } = { \left ( { y - 1 } \right ) ^ { \frac { 1 } { 2 } } } } $$

$$ { \large \sqrt { 1 + { { \left ( { \frac { { d x } } { { d y } } } \right ) } ^ 2 } } = \sqrt { 1 + y - 1 } = \sqrt y } $$

در نهایت طول قوس منحنی به شکل زیر محاسبه می‌شود.

$$ { \large \begin {align*} L & = \int _ { { \, 1 } } ^ { { \, 4 } } { { \sqrt y \, d y } } \\ & = \left. { \frac { 2 } { 3 } { y ^ { \frac { 3 } { 2 } } } } \right | _ 1 ^ 4 \\ & = \frac { { 1 4 } } { 3 } \end {align*} } $$

مثال 3

طول قوس منحنی تابع $$ { x = \frac { 1 } { 2 } { y ^ 2 } } $$ را در محدوده $$ { 0 \le x \le \frac { 1 } { 2 } } $$ محاسبه کنید. برای محاسبه این طول، فرض کنید که y مقادیر مثبت را در بر می‌گیرد.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

برای محاسبه طول قوس منحنی، ابتدا مشتق x نسبت به y را به شکل زیر مورد محاسبه قرار می‌دهیم.

$$ { \large \frac { { d x } } { { d y } } = y } $$

$$ { \large \sqrt { 1 + { { \left ( { \frac { { d x } } { { d y } } } \right ) } ^ 2 } } = \sqrt { 1 + { y ^ 2 } } } $$

توجه کنید که در این حالت، نیاز به تعیین محدوده‌ تغییرات y برای محاسبه انتگرال فوق داریم. با توجه به محدوده تغییرات x می‌توان نتیجه گرفت که y در بازه زیر قرار دارد.

$$ { \large 0 \le y \le 1 } $$

بنابراین می‌توان بیان کرد که انتگرال مربوط به محاسبه طول قوس منحنی به شکل زیر نوشته می‌شود.

$$ { \large L = \int _ { { \, 0 } } ^ { { \, 1 } } { { \sqrt { 1 + { y ^ 2 } } \, d y } } } $$

توجه کنید که این انتگرال را به شکل زیر و با استفاده از تغییر متغیر $$ { y = \tan \theta } $$ می‌توان مورد محاسبه قرار داد. برای این کار روندی که در ادامه توضیح داده شده را طی کنید.

$$ { \large y = \tan \theta \hspace { 0.5 in } d y = { \sec ^ 2 } \theta \, d \theta } $$

$$ { \large \begin {align*} y & = 0 & \hspace { 0.25 in } \Rightarrow \hspace { 0.25 in } 0 = \tan \theta \hspace { 0.25 in } \Rightarrow \hspace { 0.25 in } \theta = 0 \, \, \, \\ y & = 1 & \hspace { 0.25 in } \Rightarrow \hspace { 0.25 in }1 = \tan \theta \hspace { 0.25 in } \Rightarrow \hspace { 0.25 in } \theta = \frac { \pi }{ 4 } \end {align*} } $$

$$ { \large \begin {align*} \sqrt { 1 + { y ^ 2 } } & = \sqrt { 1 + { { \tan } ^ 2 } \theta } \\ & = \sqrt { { { \sec } ^ 2 } \theta } \\ & = \left | { \sec \theta } \right | \\ & = \sec \theta \end {align*} } $$

در ادامه، روابط محاسبه شده در بالا را در رابطه انتگرالی قرار می‌دهیم. بنابراین طول قوس منحنی به شکل زیر محاسبه می‌شود.

$$ { \large \begin {align*} L & = \int _ { { \, 0 } } ^ { { \, \frac { \pi } { 4 } } } { { { { \sec } ^ 3 } \theta \, d \theta } } \\ & = \left. { \frac { 1 } { 2 } \left ( { \sec \theta \tan \theta + \ln \left | { \sec \theta + \tan \theta } \right | } \right ) } \right | _ 0 ^ { \frac { \pi } { 4 } } \\ & = \frac { 1 } { 2 } \left ( { \sqrt 2 + \ln \left ( { 1 + \sqrt 2 } \right ) } \right ) \end {align*} } $$

همانطور که مشاهده می‌شود، انتگرال فوق یک انتگرال مثلثی بود که برای محاسبه آن از روش تغییر متغیر استفاده شد. توجه کنید که روش تغییر متغیر به صورت دقیق در مطلب «تغییر متغیر — به زبان ساده» در وبلاگ فرادرس مورد مطالعه قرار گرفته است.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• قطاع و مقطع دایره و محاسبات آن در هندسه — به زبان ساده و تصویری
• قدر مطلق — به زبان ساده
• مشتق — به زبان ساده
• انتگرال — به زبان ساده
• دامنه و برد تابع — به زبان ساده

^^