انتگرال گیری به روش کسرهای جزئی — از صفر تا صد

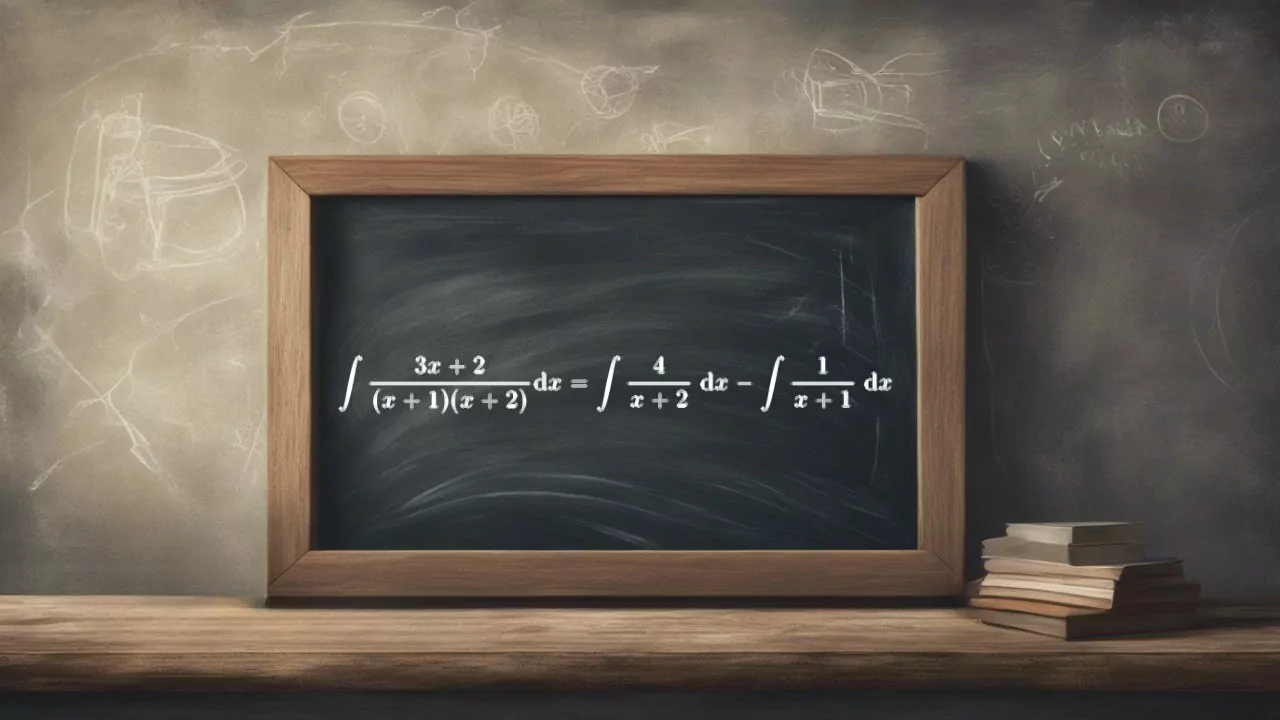
در مطالب قبلی وبلاگ فرادرس، اصول و روش‌های تجزیه کسر به صورت دقیق مورد مطالعه قرار گرفت. همانطور که اشاره شد، تجزیه کسر با استفاده از کسرهای جزئی، کاربرد بسیار زیادی در محاسبه انتگرال دارد و این مبحث با عنوان انتگرال گیری به روش کسرهای جزئی در ریاضیات مورد بررسی قرار می‌گیرد.

این مطلب ابتدا به صورت دقیق، به بررسی انتگرال گیری به روش کسرهای جزئی می‌پردازد. در ادامه، قوانین مختلف مورد استفاده در تجزیه کسر به کسرهای جزئی نیز به صورت جامع مطالعه می‌شوند و در انتهای مطلب نیز با استفاده از چندین مثال، حالات مختلف موجود در انتگرال گیری به روش کسرهای جزئی مورد بررسی قرار می‌گیرند.

انتگرال گیری به روش کسرهای جزئی

حالتی را در نظر بگیرید که عبارت جلوی انتگرال به صورت یک کسر باشد. اگر در این حالت، با استفاده از روش‌های مرسوم نتوان انتگرال را محاسبه کرد، باید از روش کسرهای جزئی و تجزیه کسر برای محاسبه این انتگرال بهره گرفت.

در واقع همانطور که در مطلب تجزیه کسر موجود در وبلاگ فرادرس اشاره شد، برای تجزیه یک کسر به کسرهای جزئی، باید روندی دقیقا مخالف جمع دو کسر طی شود. بنابراین جمع دو کسر به شکل زیر را در نظر بگیرید.

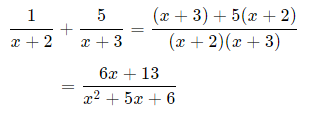
در این قسمت، هدف این است که از سمت راست رابطه بالا به سمت چپ آن برسیم. بنابراین عبارت اولیه مد نظر ما عبارت زیر است.

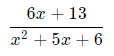
در ادامه و به کمک روش‌های مختلف اشاره شده درمطلب پیش رو، به دنبال رسیدن به کسرهای جزئی تشکیل دهنده عبارت بالا هستیم. این دو کسر برابر با کسرهای زیر هستند.

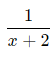
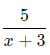
در ریاضیات، به دو کسر بالا، کسرهای جزئی عبارت $${6 x + 13} \over {x ^ 2 + 5 x + 6}$$ گفته می‌شود. بنابراین با توجه به توضیحاتی که داده شد، هدف ما از تجزیه یک کسر به کسرهای جزئی شامل دو مورد زیر است.

• تجزیه یک کسر به کسرهای جزئی، محاسبه انتگرال‌های خاصی را بسیار آسان و ساده می‌کند.
• روش تجزیه کسر به کسرهای جزئی، کاربرد بسیار زیادی در محاسبات مربوط به تبدیل لاپلاس دارد. «تبدیل لاپلاس» در مطالب دیگر موجود در وبلاگ فرادرس به صورت کامل مورد مطالعه قرار گرفته است.

بنابراین در صورتی که ما نیاز به انتگرال‌گیری از رابطه داده شده را داشته باشیم، تنها کافی است که با استفاده از روش تجزیه کسر، عبارت داده شده را به صورت مجموع دو کسر جزئی بیان کنیم. این موضوع در رابطه زیر نشان داده شده است.

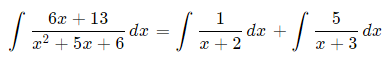
حال با استفاده از روش‌های انتگرال‌گیری رایج، انتگرال دو کسر داده شده را محاسبه می‌کنیم. همانطور که می‌دانیم انتگرال یک کسر به صورت تابع ln است. بنابراین داریم:

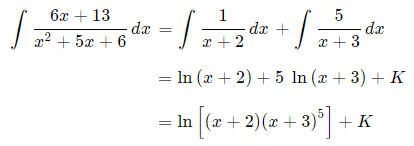
تابع اولیه و انتگرال آن به ترتیب در شکل‌های زیر نشان داده شده‌اند. توجه کنید که نمودار انتگرال این تابع، برای حالتی رسم شده که عدد K برابر با 10 است.

در ادامه به بیان قوانین مختلف هنگام انتگرال گیری به روش کسرهای جزئی پرداخته می‌شود. بنابراین یک رابطه کسر گویا به شکل زیر را در نظر بگیرید.

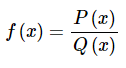
در این کسر، (P(x و (Q(x چند جمله‌ای هستند و درجه (P(x کمتر از درجه (Q(x‌ است. درجه یک چند جمله‌ای در مطلب «چندجمله‌ای‌ها – به زبان ساده» به خوبی مورد بررسی قرار گرفته است. توجه کنید که درجه یک چند جمله‌ای برابر بزرگترین توان موجود در چندجمله‌ای است. بنابراین به یاد داشته باشید که روش تجزیه کسر به کسرهای جزئی، تنها در حالتی کاربرد دارد که درجه صورت از مخرج کمتر باشد. این موضوع یکی از نکات بسیار مهم و کلیدی در تجزیه کسر و انتگرال گیری به روش کسرهای جزئی است.

بنابراین در صورتی که شرط بالا برقرار باشد، مخرج کسر را به روش‌های مختلف و با استفاده از اتحاد‌ها، فاکتورگیری می‌کنیم. در ادامه، برای هرکدام از فاکتورهای موجود در مخرج، از جدول زیر استفاده می‌کنیم و کسرهای جزئی را به دست می‌آوریم.

توجه کنید که سطر اول و سوم موجود در جدول بالا، حالات خاصی از سطر دوم و چهارم را نشان می‌دهند. همچنین روش‌های زیادی برای محاسبه ضرایب کسرهای جزئی در جدول بالا موجود است. برای بررسی بیشتر این روش‌ها، چند مثال مختلف برای محاسبه انتگرال‌ها آورده شده است.

مثال 1

انتگرال زیر را محاسبه کنید.

اولین گام برای محاسبه انتگرال بالا این است که عبارت موجود در مخرج را تا جای ممکن، تجزیه و فاکتورگیری کنیم. بنابراین می‌توان این کسر را به شکل تجزیه شده زیر بیان کرد.

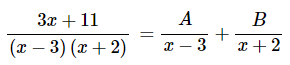
همانطور که مشاهده می‌شود، با توجه به حضور عبارتی مشابه با سطر اول جدول بالا، می‌توان از این سطر برای تجزیه رابطه داده شده، استفاده کرد. برای محاسبه ضرایب این دو عبارت، ابتدا کسرهای موجود در سمت راست معادله بالا را با یکدیگر هم مخرج می‌کنیم. بنابراین می‌توان کسر بالا را به شکل زیر بیان کرد.

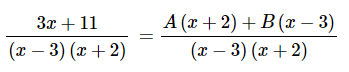
بنابراین صورت دو کسر بالا را می‌توان با یکدیگر برابر قرار داد. این موضوع در رابطه زیر نشان داده شده است.

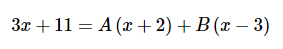
در ادامه و برای محاسبه ضرایب A و B، ریشه دو عبارت (x+2) و (x-3) را در رابطه بالا قرار می‌دهیم. ریشه عبارت (x+2) برابر با 2- و ریشه عبارت (x-3) برابر با 3 است. بنابراین با قرار دادن این دو ریشه در رابطه بالا داریم:

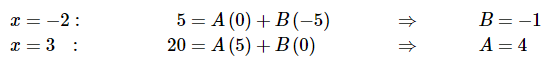
بنابراین همانطور که مشاهده می‌شود، با انتخاب دقیق و درست پارامتر x، ضرایب A و B به راحتی محاسبه شدند. در صورتی که مقادیر دیگری برای x انتخاب می‌شد، باید یک دستگاه دو معادله و دو مجهول را حل می‌کردیم.

با توجه به روابطی که در بالا ذکر شد، انتگرال اولیه در صورت سوال را می‌توانیم به شکل زیر بازنویسی کنیم.

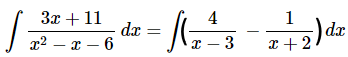
بر این اساس، انتگرال موجود در سمت راست معادله بالا را می‌توانیم به شکل زیر محاسبه کنیم.

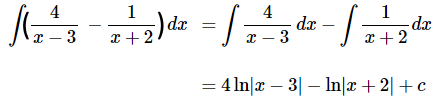
برای محاسبه انتگرال، از این نکته استفاده شده که انتگرال تابع $$ { 1 \over v } $$ برابر با $$ \ln | v | $$ است. بنابراین ایده اصلی محاسبه انتگرال، استفاده از تغییر متغیر است. در واقع پارامتر v را یک بار برابر با x-3 و بار دیگر برابر با x+2 قرار دهیم.

توجه کنید که بسیاری از مثال‌های موجود در مبحث انتگرال گیری به روش کسرهای جزئی به انتگرال نهایی بالا ختم می‌شود. بنابراین حتما مثال بالا را بارها خودتان حل کنید و مطمئن شوید که می‌توانید انتگرال نهایی را به درستی محاسبه کنید.

نکته دیگری که در مبحث انتگرال گیری به روش کسرهای جزئی باید به آن توجه کرد این است که بسیاری از مثال‌ها، در نهایت به رابطه زیر ختم می‌شوند. بنابراین دانستن شیوه محاسبه این انتگرال، امری ضروری است.

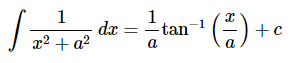
در ادامه مثالی عمیق‌تر بیان می‌شود که برای محاسبه آن نیاز به استفاده از مبحث انتگرال گیری به روش کسرهای جزئی داریم.

مثال 2

انتگرال زیر را محاسبه کنید.

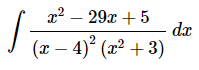
محاسبه این انتگرال به شیوه مستقیم کار بسیار پیچیده‌ای است. بنابراین ما از مبحث انتگرال گیری به روش کسرهای جزئی برای محاسبه انتگرال بالا استفاده می‌کنیم. در این مثال، مخرج کسر موجود در صورت سوال فاکتورگیری شده است. بنابراین تنها ما باید کسرهای جزئی آن را تشکیل دهیم. این موضوع در رابطه زیر نشان داده شده است.

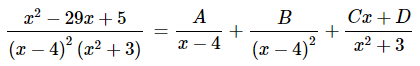
توجه کنید که برای نوشتن این کسرهای جزئی از نکات موجود در سطر دوم و سوم جدول بالا استفاده شده است. در ادامه، دو طرف رابطه بالا را در عبارت $$ ( x - 4 ) ^ 2 ( x ^ 2 + 3 ) $$ ضرب می‌کنیم. این موضوع در رابطه زیر به تصویر کشیده شده است.

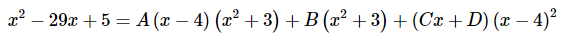
در ادامه ابتدا ضرب پرانتز‌های مختلف در یکدیگر را انجام می‌دهیم و بعد از آن رابطه را مرتب می‌کنیم. در نهایت رابطه فوق به شکل زیر در می‌آید.

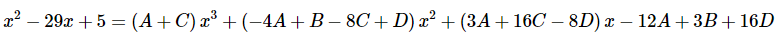
حال، ضرایب $$ x ^ 3 $$ در دو طرف رابطه را با یکدیگر برابر قرار می‌دهیم. این کار را برای ضرایب $$ x ^ 1 $$ ،$$ x ^ 2 $$ و  $$ x $$ نیز تکرار می‌کنیم. همچنین اعداد ثابت در دو طرف رابطه بالا را نیز با یکدیگر برابر قرار می‌دهیم. بنابراین با انجام اعمالی که در بالا توضیح داده شد، یک دستگاه چهار معادله و چهار مجهول به دست می‌آید. این موضوع در رابطه زیر نشان داده است.

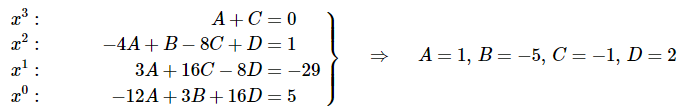
توجه کنید که ضرایب مربوط به $$ x ^ 0 $$ همان ثابت‌های موجود در دو طرف رابطه را نشان می‌دهد.

بنابراین با توجه به محاسبات انجام شده، می‌توانیم انتگرال ابتدای مثال را به شکل زیر بازنویسی کنیم.

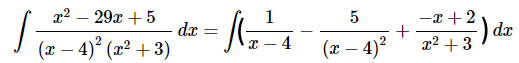
عبارت آخر رابطه بالا، یعنی $$ {-x + 2} \over {x ^ 2 + 3}$$ را به صورت جمع دو عبارت $$ {-x } \over {x ^ 2 + 3}$$ و $$ { 2 } \over {x ^ 2 + 3}$$ می‌نویسیم. این موضوع در رابطه زیر نشان داده شده است.

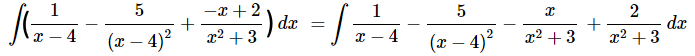
حال می‌توانیم انتگرال بالا را محاسبه کنیم. انتگرال عبارت اول و سوم موجود در سمت راست معادله بالا برابر با یک عبارت لگاریتمی می‌شود. برای محاسبه انتگرال عبارت دوم نیز از روابط رایج موجود در مبحث انتگرال استفاده می‌کنیم. همچنین عبارت چهارم نیز با استفاده از نکته بیان شده در قسمت قبل این مثال، محاسبه می‌شود. این نکته در رابطه زیر تکرار شده است.

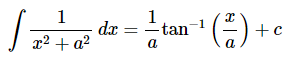
بنابراین فرم نهایی انتگرال صورت سوال به شکل زیر در می‌آید.

توجه کنید که برای محاسبه دو عبارت اول در انتگرال فوق از تغییر متغیر u=x-4 و برای محاسبه دو عبارت انتهای انتگرال فوق از تغییر متغیر v=x²+3 استفاده کردیم.

نکته مهمی که در ابتدای این بخش بیان شد این است که مبحث انتگرال گیری به روش کسرهای جزئی در حالتی کاربرد دارد که درجه صورت کسر مورد نظر از درجه مخرج آن کمتر باشد. اما این شرط در تمام کسرها صادق نیست و در برخی از کسرها درجه صورت از درجه مخرج بیشتر است. برای انتگرال‌گیری از این مدل کسرها، به روش کسرهای جزئی، نیاز به استفاده از یک روش خاص داریم. این موضوع در مثال زیر مورد مطالعه قرار گرفته است.

مثال 3

انتگرال نامعین زیر را محاسبه کنید.

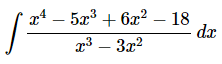
همانطور که مشاهده می‌شود، درجه صورت برابر با 4 و درجه مخرج برابر با 3 است. بنابراین درجه صورت از مخرج بیشتر است. بنابراین در این شرایط نمی‌توان از مبحث انتگرال گیری به روش کسرهای جزئی برای محاسبه این انتگرال استفاده کرد.

برای حل کردن این مشکل دو راه موجود است. راه اول این است که صورت کسر را بر مخرج آن تقسیم کنیم و عبارت را به فرم ساده‌تری بنویسیم. راه دوم نیز این است که صورت کسر را با استفاده از روش‌های رایج فاکتورگیری و استفاده از اتحاد‌ها تجزیه کنیم. در این مثال از روش دوم استفاده می‌کنیم. بنابراین ابتدا از عبارات x² موجود در صورت و مخرج فاکتور می‌گیریم.

$$ { x ^ 2 ( x ^ 2 - 5 x + 6 ) -18 } \over { x ^ 2 ( x - 3 ) }$$

حال با استفاده از تجزیه چند جمله‌ای درجه دو، صورت رابطه بالا را به فرم ساده‌تری بیان می‌کنیم. بنابراین داریم.

$$ { x ^ 2 ( x - 3 ) ( x - 2 ) -18 } \over { x ^ 2 ( x - 3 ) }$$

در ادامه کسر نشان داده شده در رابطه بالا را به صورت دو کسر مجزا از هم تجزیه می‌کنیم.

$${ { x ^ 2 ( x - 3 ) ( x - 2 ) } \over { x ^ 2 ( x - 3 ) } } - {18 \over x ^ 2 ( x - 3 ) }$$

حال می‌توانیم صورت و مخرج عبارت اول موجود در رابطه فوق را به شکل ساده شده بیان کنیم. بنابراین فرم نهایی رابطه ابتدای مثال، به شکل ساده شده زیر در می‌آید.

بر این اساس می‌توانیم انتگرال موجود در مثال را به شکل زیر بازنویسی کنیم.

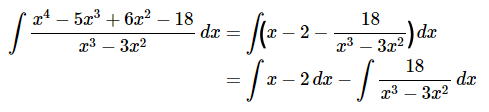
عبارت اول در فرم نهایی انتگرال (عبارت اول سمت راست رابطه بالا) به سادگی با استفاده از روابط رایج انتگرال‌گیری محاسبه می‌شود و برای محاسبه عبارت دوم، از قواعد انتگرال گیری به روش کسرهای جزئی استفاده می‌کنیم. بنابراین کسرهای جزئی را به شکل زیر می‌نویسیم.

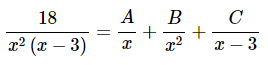
طرفین رابطه بالا را در عبارت $$ x ^ 2 ( x - 3 )$$ (مخرج عبارت سمت چپ رابطه بالا) ضرب می‌کنیم. بنابراین داریم:

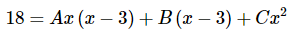
برای محاسبه ضرایب موجود در رابطه بالا دو روش موجود است. روش اول این است که به x مقادیر مختلفی بدهیم و با استفاده از معادلات به دست آمده، ضرایب B ،A و C را محاسبه کنیم و روش دوم نیز این است که مانند مثال قبل، ضریب توان‌های مختلف x در دو طرف رابطه را با یکدیگر برابر قرار دهیم. در اینجا، از روش اول استفاده می‌کنیم. بنابراین داریم:

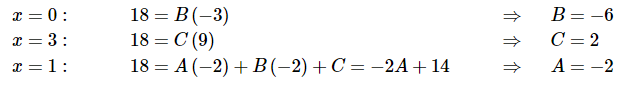
توجه کنید که مقادیر $$ x = 3$$ و $$ x = 0$$ که برای محاسبه ضرایب انتخاب شدند، به ترتیب ریشه عبارت $$ x - 3 $$ و $$ x ^ 2 $$ هستند و $$ x = 1 $$ نیز یک مقدار دلخواه را نشان می‌دهد. در نهایت انتگرال ابتدای این مثال به شکل زیر در می‌آید.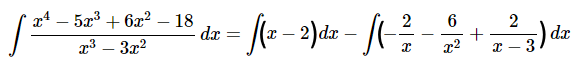 

همانطور که مشاهده می‌شود، با طی شدن روندی که توضیح داده شد، می‌توانیم انتگرال یک کسر که درجه صورت آن بیشتر از درجه مخرج است را مورد محاسبه قرار دهیم. بنابراین پاسخ مسئله به شکل زیر قابل نمایش است.

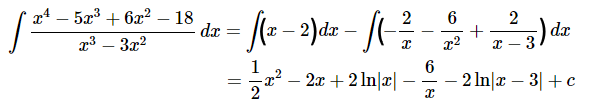
در مثال بالا (مثال ۳) و هنگام تجزیه کسر، عبارت $$x ^ 2$$ در مخرج مشاهده می‌شود و برای بیان کسر جزئی آن می‌توان از دو روش استفاده کرد. روش اول این است که $$x ^ 2$$ را به عنوان یک چند جمله‌ای درجه ۲ (سطر سوم جدول ابتدای مطلب) در نظر بگیریم و کسر جزئی آن را به شکل زیر بیان  کنیم.

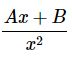
راه دیگر این است که این عبارت $$x ^ 2$$ را به عنوان یک عبارت خطی (سطر دوم جدول ابتدای مطلب) به فرم زیر در نظر بگیرم.

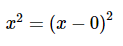
در این حالت، کسرهای جزئی را می‌توان به شکل زیر بیان کرد.

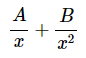
در مثال بالا (مثال ۳)، از روش دوم برای بیان کسرهای جزئی عبارت $$x ^ 2$$ استفاده شده است. توجه کنید که در این مثال، خیلی تفاوتی نمی‌کند که از کدام روش استفاده شود ولی در مثال‌های دیگر و زمانی که $$x ^ 3$$ و $$x ^ 4$$ داریم، روش دوم، روش ساده‌تری محسوب می‌شود. دلیل این موضوع، حضور ترم‌های معروف در کسر جزئی آن است. این مورد در روابط زیر نشان داده شده است.

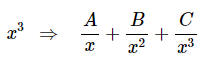
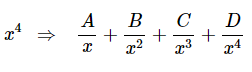
حال به یک مثال دیگر توجه کنید تا به درک کامل و درست از مطلب انتگرال گیری به روش کسرهای جزئی دست پیدا کنید.

مثال 4

انتگرال زیر را محاسبه کنید.

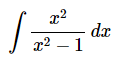
همانطور که مشاهده می‌شود درجه صورت و مخرج در این مثال با یکدیگر برابر هستند. بنابراین مشابه با مثال قبل باید کاری کنیم که درجه صورت از درجه مخرج کمتر شود. بنابراین می‌توانیم کسر فوق را به شکل زیر بازنویسی کنیم.

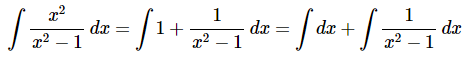
در ادامه می‌توانیم عبارت دوم سمت راست معادله بالا را به صورت کسرهای جزئی بنویسیم. بنابراین قدم اول این است که مخرج کسر را به صورت تجزیه شده بنویسیم. بنابراین از اتحاد مزدوج برای این کار استفاده می‌کنیم. این موضوع در رابطه زیر نشان داده شده است.

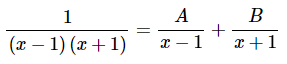
طرفین رابطه فوق را در $$ ( x - 1 ) ( x + 1 ) $$ ضرب می‌کنیم. بنابراین داریم:

با قرار دادن ریشه دو عبارت $$ ( x - 1 ) $$ و $$ ( x + 1 ) $$ در رابطه فوق، دو ضریب A و  B به شکل زیر محاسبه می‌شوند.

در نهایت و با قرار دادن ضرایب و عبارات بالا در رابطه صورت سوال، انتگرال خواسته شده به صورت زیر محاسبه می‌شود.

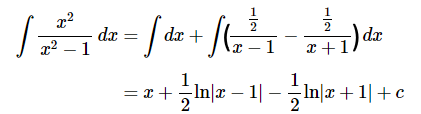
بنابراین همانطور که در تمام مثال‌ها نشان داده شد، اولین گام در انتگرال گیری به روش کسرهای جزئی این است که کسر داده شده را تجزیه کنیم. تجزیه یک کسر در ریاضیات قوانین خاص خود را دارد که در مطلب «تجزیه کسر — به زبان ساده» مورد مطالعه قرار گرفته است.

این مطلب ابتدا به صورت دقیق، به بررسی مفاهیم انتگرال گیری به روش کسرهای جزئی پرداخته است. در ادامه قوانین مختلف مورد استفاده در تجزیه کسر به کسرهای جزئی و کاربردهای گوناگون این عمل به صورت دقیق مطالعه شدند و در انتهای مطلب نیز با استفاده از چندین مثال، حالات مختلف موجود در انتگرال گیری به روش کسرهای جزئی مورد مطالعه قرار گرفتند.