حل معادله نمایی — به زبان ساده
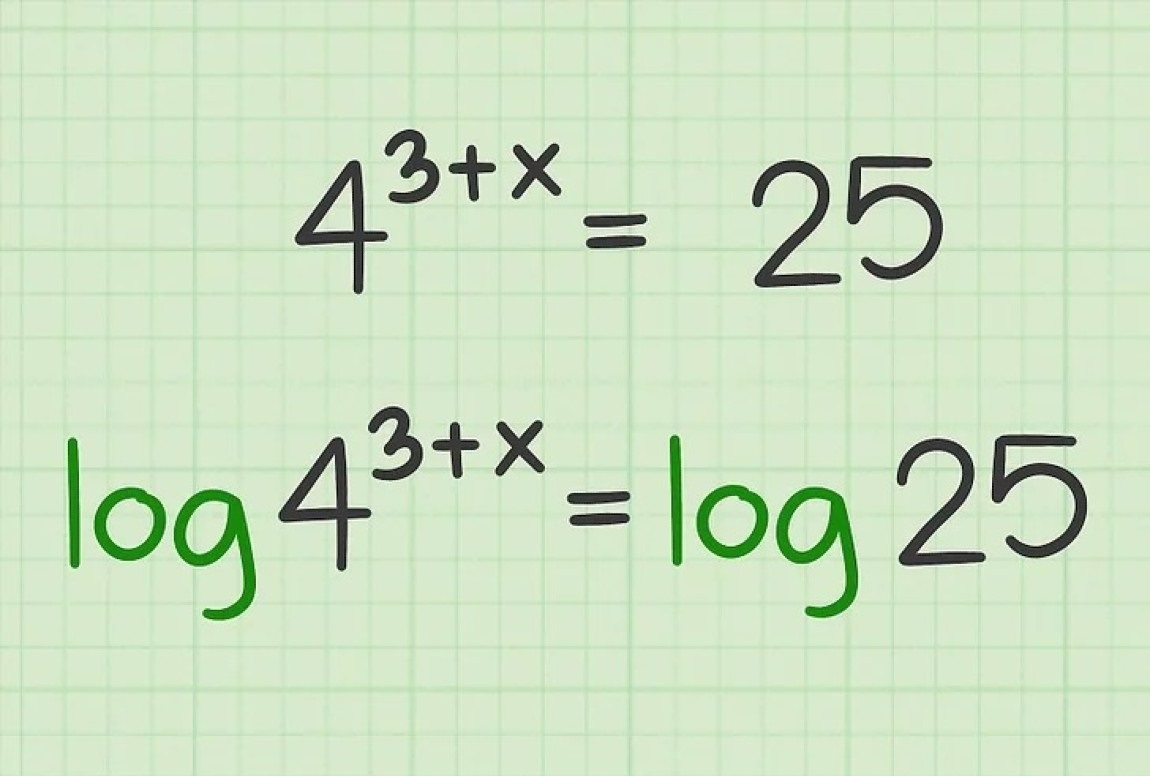
در مطالب قبلی از مجموعه آموزشهای ریاضی مجله فرادرس با حل معادلات لگاریتمی، چندجملهایهای درجه دوم، درجه سوم و درجه چهارم آشنا شدیم. گاهی با معادلاتی روبهرو میشویم که جملاتی دو طرف تساوی عبارتهایی نمایی هستند. در این آموزش، با روشهای حل معادله نمایی آشنا میشویم و مثالهای متنوعی را درباره آن حل خواهیم کرد.
قوانین توابع نمایی
چند مورد از قوانین مربوط به توابع نمایی به شرح زیر است:
- (۱) $$ a ^ m \times a ^ n = a ^ { m + n } $$
- (۲) $$ a ^ m \div a ^ n = a ^ { m - n } $$
- (۳) $$ ( a ^ m ) ^ n = a ^ { m n } $$
- (۴) $$ ( a b ) ^ n = a ^ { n } b ^ { n } $$
- (۵) $$ a ^ 0 = b ^ 0 $$
- (۶) $$ 1 ^ m = 1 ^ n $$
حل معادله نمایی با پایه مشابه
برای حل معادله نمایی با پایه مشابه، در اغلب موارد، قضیه زیر کارآمد است.
قضیه: اگر $$ a $$ یک ثابت غیرصفر بوده و معادله $$ a ^ x = a ^ y $$ را داشته باشیم، آنگاه $$ x = y $$.
اثبات: به سادگی داریم:
$$ \large \begin {aligned} a ^ x & = a ^ y , a \neq 1 \\ \frac { a ^ x } { a ^ y } & = 1 \\ a ^ { x - y } & = 1 \\ x - y & = 0 \\ x & = y . \ _ \square \end {aligned} $$
در واقع، برای حل معادله نمایی ابتدا تغییرات لازم را با استفاده از قانون نماییها و چند قضیه ساده در جبر بر معادله اعمال میکنیم و آن را به فرم استاندار قضیه مینویسیم. سپس، در گام بعدی از قضیه بالا استفاده کرده و معادله را حل میکنیم.
مثالهای حل معادله نمایی با پایههای مشابه
در این بخش، ٰمثالهایی از معادله نمایی با پایههای مشابه را حل میکنیم.
مثال ۱: معادله $$ \displaystyle { \frac { 1 } { 5 ^ { x - 1 } } = 1 2 5 } $$ را حل کنید.
حل: پایه دو طرف تساوی را میتوان به $$ 5 $$ تبدیل کرد:
$$ \large \begin {aligned} \frac { 1 } { 5 ^ { x - 1 } } & = 1 2 5 \\ 5 ^ { - ( x - 1 ) } & = 5 ^ 3 \\ - ( x - 1 ) & = 3 \\ x & = - 2 . \ _ \square \end {aligned} $$
مثال ۲: معادله $$ 4 ^ { x - 3 } = 0 . 1 2 5 $$ را حل کنید.
حل: با تبدیل پایههای دو طرف به $$ 2 $$، خواهیم داشت:
$$ \large \begin {aligned} 4 ^ { x - 3 } & = 0 . 1 2 5 \\ 4 ^ { x - 3 } & = \frac { 1 2 5 } { 1 0 0 0 } \\ 2 ^ { 2 x - 6 } & = \frac { 1 } { 8 } \\ 2 ^ { 2 x - 6 } & = 2 ^ { - 3 } \\ 2 x - 6 & = - 3 \\ x & = \frac { 3 } { 2 } . \ _ \square \end {aligned} $$
مثال ۳: مقدار $$ x $$ را از معادله $$ 4 ^ x = 16 $$ به دست آورید.
حل: داریم:
$$ \large 4 ^ x = 1 6 \Rightarrow 4 ^ x = 4 ^ 2 $$
طبق قضیهای که گفتیم، $$ x = 2 $$ خواهد بود.
مثال ۴: اگر $$ 8 ^ x = 2 $$ باشد، آنگاه مقدار $$ x $$ را به دست آورید.
حل: داریم:
$$ \large \begin {aligned} 8 ^ x & = 2 \\ \big ( 2 ^ 3 \big ) ^ { x } & = 2 \\ 2 ^ { 3 x } & = 2 ^ { 1 } . \end {aligned} $$
مقدار $$ x $$ با برابر قرار دادن توانها به دست میآید:
$$ \large \begin {aligned} 3 x & = 1 \\ x & = \dfrac { 1 } { 3 } . \ _ \square \end {aligned} $$
مثال ۵: اگر $$ 6 ^ x - 1 = 0 $$ باشد، مقدار $$ x $$ چقدر است؟
حل: جواب به سادگی به صورت زیر به دست میآید:
$$ \large \begin {aligned} 6 ^ x - 1 & = 0 \\ 6 ^ x & = 1 \\ 6 ^ x & = 6 ^ 0 \\ x & = 0 . \ _ \square \end {aligned} $$
مثال ۶: اگر $$ ( 8 ) ( 9 ^ x ) = 9 ^ x $$ باشد، آنگاه مقدار $$ x $$ را به دست آورید.
حل: داریم:
$$ \large \begin {aligned} ( 8 ) ( 9 ^ x ) & = 9 ^ x \\ ( 8 ) ( 9 ^ x ) - 9 ^ x & = 0 \\ ( 7 ) 9 ^ x & = 0 \\ 9 ^ x & = 0 . \end {aligned} $$
از این قضیه استفاده میکنیم که «اگر $$ a \neq 0 $$ و $$ a ^ x = 0 $$، آنگاه $$ x = \phi $$». بنابراین، $$ x = \phi $$ یا همان تهی است.
حل معادله نمایی با پایههای متفاوت
اگر پایهها متفاوت باشند، تکنیکهای دیگری برای حل این معادله نمایی وجود دارد. مثلاً گاهی میتوان پایههای متفاوت را به یک پایه مشابه تبدیل کرد و جواب را مانند قسمت قبل به دست آورد. در مثالهایی که در ادامه حل میکنیم، این روشها را بهتر یاد میگیریم.
مثالهای حل معادله نمایی با پایههای متفاوت
در این بخش، ٰمثالهایی از معادله نمایی با پایههای متفاوت را حل میکنیم.
مثال ۱: معادله $$ 4 ^ { 3 x } = 8 ^ { x - 1 } $$ را حل کنید.
حل: میبینیم که دو پایه متفاوت $$ 4 $$ و $$ 8 $$ داریم. هر دوی این پایهها را میتوان به $$ 2 $$ تبدیل کرد. با این کار، خواهیم داشت:
$$ \large \begin {aligned} 4 ^ { 3 x } & = 8 ^ { x - 1 } \\ \big ( 2 ^ 2 \big ) ^ { 3 x } & = \big ( 2 ^ 3 \big ) ^ { x - 1 } \\ 2 ^ { 6 x } & = 2 ^ { 3 x - 3 } \\ 6 x & = 3 x - 3 \\ x & = - 1 . \ _ \square \end {aligned} $$
مثال ۲: مقدار $$ x $$ را از معادله $$ \dfrac { 8 ^ { 4 x - \sqrt { x } } } { { 1 6 } ^ { 2 x + \sqrt { x } } } = 2 ^ { 2 \sqrt { x } } $$ به دست آورید.
حل: داریم:
$$ \large \begin {aligned} \dfrac { 8 ^ { 4 x - \sqrt { x } } } { { 1 6 } ^ { 2 x + \sqrt { x } } } & = 2 ^ { 2 \sqrt { x } } \\ \\ \dfrac { { \big ( 2 ^ 3 \big ) } ^ { 4 x - \sqrt { x } } } { { { \big ( 2 ^ 4 \big ) } } ^ { 2 x + \sqrt { x } } } & = 2 ^ { 2 \sqrt { x } } \\ \\ \dfrac { 2 ^ { 1 2 x - 3 \sqrt { x } } }{ 2 ^ { 8 x + 4 \sqrt { x } } } & = 2 ^ { 2 \sqrt { x } } \\ \\ 2 ^ { 1 2 x - 3 \sqrt { x } - 8 x - 4 \sqrt { x } } & = 2 ^ { 2 \sqrt { x } } \\ \\ 2 ^ { 4 x - 7 \sqrt { x } } & = 2 ^ { 2 \sqrt { x } } . \end {aligned} $$
اکنون پایهها مشابه هستند. با برابر قرار دادن توانها، خواهیم داشت:
$$
4x-7\sqrt { x } = 2 \sqrt { x }
$$
$$
4x = 9 \sqrt { x }
$$
$$
16 x ^ 2 = 81 x
$$
$$
16 x ^ 2 - 81 x = 0
$$
$$
x ( 16 x - 81 ) = 0
$$
$$ x = 0 $$
$$
16 x - 81 = 0 \to x = \frac { 81 } { 16 }
$$
مثال ۳: معادله لگاریتمی زیر را حل کنید:
$$ \large \frac { 2 7 ^ { 3 x - 2 } } { 2 4 3 } = 8 1 ^ { 3 x - 6 } . $$
با تبدیل پایههای اعداد $$ 27 $$، $$ 81 $$ و $$ 243 $$ به $$ 3 $$، خواهیم داشت:
$$ \large \begin {aligned} \frac { 2 7 ^ { 3 x - 2 } } { 2 4 3 } & = 8 1 ^ { 3 x - 6 } \\ \frac { 3 ^ { 9 x - 6 } } { 3 ^ 5 } & = 3 ^ { 1 2 x - 2 4 } \\ 3 ^ { 9 x - 6 - 5 } & = 3 ^ { 1 2 x - 2 4 } \\ 3 ^ { 9 x - 1 1 } & = 3 ^ { 1 2 x - 2 4 } \\ 9 x - 1 1 & = 1 2 x - 2 4 \\ 3 x & = 1 3 \\ x & = \frac { 1 3 } { 3 } . \ _ \square \end {aligned} $$
متأسفانه، تبدیل پایهها به یک پایه مشترک مطابق آنچه در مثالهای بالا دیدیم، همیشه ممکن نیست.
برای مثال، در حل $$ 5 ^ x = 3 ^ { x + 2 } $$، میبینیم که پایهها متفاوت هستند و نمیتوان آنها را به یک پایه مشترک تبدیل کرد. در این موارد، باید از لگاریتمها استفاده کنیم. مثالهای زیر این موضوع را به خوبی نشان میدهند.
مثال ۴: معادله $$ 5 ^ x = 3 ^ { x + 2 } $$ را حل کنید.
حل: با توجه به اینکه پایهها یکسان نیستند و نمیتوان آنها را به یک پایه مشابه تبدیل کرد، از طرفین معادله لگاریتم میگیریم:
$$ \large \begin {aligned} 5 ^ { x } & = 3 ^ { x + 2 } \\ \log _ { 1 0 } ( 5 ^ { x } ) & = \log _ { 1 0 } \big ( 3 ^ { x + 2 } \big ) \\ x \log _ { 1 0 } 5 & = ( x + 2 ) \log _ { 1 0 } 3 \\ x \log _ { 1 0 } 5 & = x \log _ { 1 0 } 3 + 2 \log _ { 1 0 } 3 \\ x \log _ { 1 0 } 5 - x \log _ { 1 0 } 3 & = 2 \log _ { 1 0 } 3 \\ x \big ( \log _ { 1 0 } 5 - \log _ { 1 0 } 3 \big ) & = 2 \log _ { 1 0 } 3 . \end {aligned} $$
بنابراین:
$$ \large x = \frac { 2 \log _ { 1 0 } 3 } { \log _ { 1 0 } 5 - \log _ { 1 0 } 3 } \approx 4.3013 . \ _ \square $$
مثال ۵: تساوی $$ 1728 = 2 ^ a . 3 ^ b $$ را در نظر بگیرید. مقادیر $$ a $$ و $$ b $$ را به دست آورید.
حل: جواب به سادگی به صورت زیر به دست میآید:
$$ \large \begin {aligned} 1 7 2 8 & = { 1 2 } ^ { 3 } \\ & = { ( 4 × 3 ) } ^ { 3 } \\ & = 4 ^ 3 × 3 ^ 3 \\ & = { ( 2 ^ 2 ) } ^ 3 × 3 ^ 3 \\ & = 2 ^ 6 × 3 ^ 3 \\ \Rightarrow a & = 6 , \ b = 3 . \ _ \square \end {aligned} $$
مثال ۶: معادله $$ 3 ^ { x ^ 2 } = 3 ^ x $$ را حل کنید.
حل: از آنجا که دو طرف معادله پایههای مشابهی دارند، نماهای آنها باید مشابه باشد:
$$ \large \begin {aligned} 3 ^ { x ^ 2 } & = 3 ^ { x } \\ x ^ 2 & = x \\ x ^ 2 - x & = 0 \\ x ( x - 1 ) & = 0 \\ \Rightarrow x & = 0 , 1 . \ _ \square \end {aligned} $$
مثال ۷: اگر $$ 2 ^ x \cdot 3 ^ y \cdot 5 ^ z = 4 5 $$، آنگاه مقدار $$ x+ y + z $$ را محاسبه کنید.
حل: میبینیم که $$ 45 $$ را میتوان به صورت زیر تجزیه کرد:
$$ \large 4 5 = 3 ^ 2 \cdot 5 = 2 ^ 0 \cdot 3 ^ 2 \cdot 5 ^ 1 . $$
در نتیجه، $$x = 0 $$، $$ y = 2 $$ و $$ z = 1 $$ خواهد بود. بنابراین، $$ x +x y + z = 0 + 2 + 1 = 3 $$ است.
مثال ۸: اگر $$ x^x \cdot y^y = 108 $$ باشد، مقدار $$ x + y $$ را به دست آورید.
حل: عدد $$ 10 8 $$ را میتوان به شکل زیر نوشت:
$$ \large 1 0 8 = 2 ^ 2 \cdot 3 ^ 3 . $$
از تساوی بالا میتوان نتیجه گرفت $$ x = 2 , y = 3 $$ یا $$ x = 3 , y = 2 $$. بنابراین، جواب $$ x + y = 2 + 3 = 5 $$ است.
مثال ۹: اگر $$ \frac { 2 ^ 5 } { 2 ^ 3 } \cdot 3 ^ 0 \cdot 3 ^ 1 \cdot 3 ^ 2 = 2 ^ x \cdot 3 ^ y $$ باشد، مقدار $$ x + y $$ را به دست آورید.
حل: عبارت کسری $$ \frac { 2 ^ 5 } { 2 ^ 3 } $$ را میتوان به صورت زیر بازنویسی کرد:
$$ \large \frac { 2 ^ 5 } { 2 ^ 3 } = { 2 } ^ { 5 - 3 } = 2 ^ 2 . \qquad ( 1 ) $$
عبارت $$ 3 ^ 0 \cdot 3 ^ 1 \cdot 3 ^ 2 $$ را نیز میتوان اینگونه نوشت:
$$ \large 3 ^ 0 \cdot 3 ^ 1 \cdot 3 ^ 2 = 3 ^ { 0 + 1 + 2 } = 3 ^ 3 . \qquad ( 2 ) $$
با توجه به $$ ( 1 ) $$ و $$ ( 2 ) $$، $$ x $$ و $$ y $$ به صورت زیر هستند:
$$ \large \begin {aligned} \frac { 2 ^ 5 } { 2 ^ 3 } \cdot 3 ^ 0 \cdot 3 ^ 1 \cdot 3 ^ 2 & = 2 ^ 2 \cdot 3 ^ 3 \\ & = 2 ^ x \cdot 3 ^ y \\ \Rightarrow x & = 2 , \ y = 3 . \end {aligned} $$
یعنی، $$ x + y = 2 + 3 = 5 $$ است.
مثال ۱۰: معادله نمایی $$ 5{{\bf{e}}^{2z + 4}} - 8 = 0 $$ را حل کنید.
حل: ابتدا معادله نمایی را به صورت زیر مینویسیم:
$$ \large {{\bf{e}}^{2z + 4}} = \frac{8}{5} $$
با توجه به وجود $$ \bf {e}$$ به عنوان پایه نمایی، از دو طرف لگاریتم طبیعی میگیریم و خواهیم داشت:
$$ \large \begin {align*} \ln { { \bf { e } } ^ { 2 z + 4 } } & = \ln \left ( { \frac {8 } { 5 } } \right ) \\ 2 z + 4 & = \ln \left ( { \frac { 8 } { 5 } } \right ) \\ 2 z & = \ln \left ( { \frac { 8 }{ 5 } } \right ) - 4 \\ z & = \frac { 1 } { 2 } \left ( { \ln \left ( { \frac { 8 } { 5 } } \right ) - 4 } \right ) = \frac { 1 } { 2 } \left ( { 0.470003629 - 4 } \right ) = - 1.76499819 \end {align*} $$











“مثالهای حل معادله نمایی با پایههای متفاوت” در مثال دوم صفر هم جواب است و در معادله صدق میکنه
با سلام و وقت بخیر؛
جواب مساله اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.