پهنای باند معادل نویز (ENBW) چیست؟ – از صفر تا صد

«پهنای باند معادل نویز» (Equivalent Noise Bandwidth) یا ENBW به صورت پهنای باند یک فیلتر Brickwall تعریف می‌شود که توان نویز مشابه با یک فیلتر واقعی تولید کند. به این پهنای باند، «پهنای باند نویز» (Noise Bandwidth) و یا «پهنای باند نویز موثر» (Effective Noise Bandwidth) نیز گفته می‌شود.

پهنای باند معادل نویز

یک سیستم با پاسخ فرکانسی $$H ( f )$$ را در نظر بگیرید. «طیف» (Spectrum) هر نویز ورودی به این سیستم توسط پاسخ فرکانسی آن شکل داده می‌شود. «نویز سفید» (White Noise) به نویزی گفته می‌شود که در تمام فرکانس‌ها، توان یکسان داشته باشد. زمانی که یک سیگنال نویز سفید گاوسی به سیستم وارد شود، خروجی آن اگرچه هنوز یک فرایند گاوسی است، اما دیگر یک فرایند سفید محسوب نمی‌شود. بلکه در این حالت مشخصه‌های فیلتر، ویژگی‌های طیفی سیگنال خروجی را تعیین می‌کند.

در یک سیستم با پاسخ فرکانسی $$H ( f )$$ «چگالی طیف توان» (Power Spectral Density) برای سیگنال خروجی به صورت زیر محاسبه می‌شود:

$$\mathcal { S } _ { Y } ( f ) = \mathcal { S } _ { X }( f ) | H ( f ) | ^ { 2 } = \frac { N _ { 0 } } { 2 } | H ( f ) | ^ { 2 }$$

حال اگر بخواهیم که مقدار توان سیگنال خروجی را محاسبه کنیم، باید از مقدار $$\mathcal { S } _ { Y } ( f )$$ انتگرال بگیریم. در نتیجه داریم:

$$P _ { Y } = \int _ { - \infty } ^ { \infty } \mathcal { S } _ { Y } ( f ) d f = \frac { N _ { 0 } } { 2 } \int _ { - \infty } ^ { \infty } | H ( f ) | ^ { 2 } d f$$

بنابراین برای محاسبه توان سیگنال خروجی از یک سیستم، لازم است مقدار انتگرال $$P _ { Y } = \int _ { - \infty } ^ { \infty } \mathcal { S } _ { Y } ( f ) d f = \frac { N _ { 0 } } { 2 } \int _ { - \infty } ^ { \infty } | H ( f ) | ^ { 2 } d f$$ را محاسبه کنیم. برای انجام این محاسبات، $$B _ { neq }$$ را تعریف می‌کنیم و آن را پهنای باند معادل نویز یک فیلتر با پاسخ فرکانسی $$H ( f )$$ می‌نامیم. مقدار $$B _ { neq }$$ بر اساس رابطه زیر محاسبه می‌شود:

$$B _ { \mathrm { n e q } } = \frac { \int _ { - \infty } ^ { \infty } | H ( f ) | ^ { 2 } d f } { 2 H _ { \mathrm { m a x } } ^ { 2 } }$$

در رابطه فوق، $$H _ { \mathrm { m a x } }$$ نشان دهنده بیشینه $$| H ( f ) |$$ در باند عبور فیلتر است. در تصویر زیر مقادیر $$B _ { \mathrm { n e q } }$$ و $$H _ { \mathrm { m a x } }$$ برای یک فیلتر معمولی نشان داده شده است.

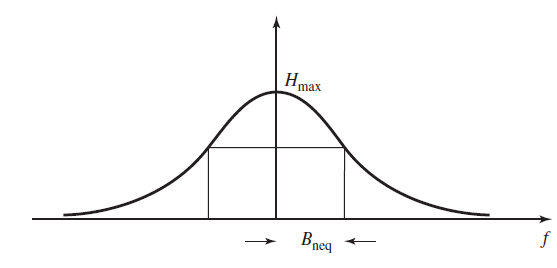$$B _ { \mathrm { n e q } }$$ و $$H _ { \mathrm { m a x } }$$ برای یک فیلتر معمولی" width="557" height="268">

با استفاده از تعاریف فوق، می‌توان نوشت:

$$\begin {aligned} P _ { Y } & = \frac { N _ { 0 } } { 2 } \int _ { - \infty } ^ { \infty } | H ( f ) | ^ { 2 } d f \\ & = \frac { N _ { 0 } } { 2 } \times 2 B _ { { n e q } } H _ { \max } ^ { 2 } \\ & = N _ { 0 } B _ { { n e q } } H _ { \max } ^ { 2 } \end {aligned}$$

بنابراین با داشتن $$B _ { neq }$$، به دست آوردن مقدار توان نویز خروجی کار ساده‌ای خواهد بود. البته به این نکته توجه کنید که مقدار پهنای باند معادل نویز فیلترها و تقویت‌کننده‌ها را معمولا کارخانه تولید کننده آن المان در اختیار کاربر قرار می‌دهد.

مثال: پهنای باند معادل نویز

پهنای باند معادل نویز یک فیلتر RC پایین گذر را به دست آورید.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

حل

پاسخ فرکانسی $$H ( f )$$ یک فیلتر پایین گذر به صورت زیر نوشته می‌شود:

$$H ( f ) = \frac { 1 } { 1 + j 2 \pi f R C}$$

در تصویر زیر پاسخ فرکانسی یک فیلتر پایین گذر نشان داده شده است.

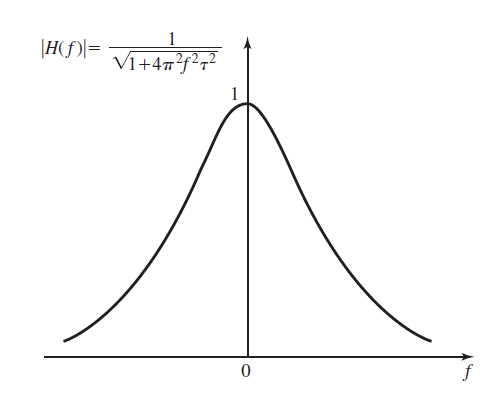
حال مقدار $$\tau = R C$$ را تعریف می‌کنیم. در نتیجه داریم:

$$| H ( f ) | = \frac { 1 } { \sqrt { 1 + 4 \pi ^ { 2 } f ^ { 2 } \tau ^ { 2 } } }$$

بنابراین $$H _ { m a x } = 1$$ خواهد بود. همچنین می‌توان رابطه زیر را برای یک فیلتر پایین گذر نوشت:

$$\begin{aligned} \int _ { - \infty } ^ { \infty } | H ( f ) | ^ { 2 } d f & = 2 \int _ { 0 } ^ { \infty } \frac { 1 } { \sqrt { 1 + 4 \pi ^ { 2 } f ^ { 2 } \tau ^ { 2 } } } d f \\ & = \frac { 2 \pi f \tau } { = } 2 \int _ { 0 } ^ { \infty } \frac { 1 } { 1 + u ^ { 2 } } \times \frac { d u } { 2 \pi \tau} \\ & = \frac { 1 } { \pi \tau} \times \frac { \pi } { 2 } \\ & = \frac { 1 } { 2 \tau } \end {aligned}$$

در نهایت پهنای باند معادل نویز به صورت زیر به دست می‌آید:

$$B _ { { n e q } } = \frac { \frac { 1 } { 2 \tau } } { 2 \times 1 } = \frac { 1 } { 4 R C }$$

پهنای باند معادل نویز برای فیلترها

رابطه مربوط به محاسبه پهنای باند معادل نویز در واقع مقدار توان نویزی را اندازه می‌گیرد که سیستم از خود عبور می‌دهد؛ زیرا مربع $$| H |$$ به توان سیگنال اشاره دارد. به این دلیل از کلمه نویز استفاده می‌کنیم که ما می‌خواهیم درباره کل طیف فرکانسی اطلاعات کسب کنیم. بنابراین پهنای باند معادل نویز مقدار توان نویزی را اندازه می‌گیرد که در پاسخ فرکانسی فیلتر انباشته شده است.

بسیاری از فیلترها با یک توان یکسان به تمام فرکانس‌های سیگنال اجازه عبور نمی‌دهند. به عنوان مثال، یک فیلتر پایین گذر به فرکانس‌های پایین با کمترین تغییرات دامنه و در نتیجه توان اجازه عبور می‌دهد، در حالی که دامنه و توان فرکانس‌های بالاتر را تضعیف می‌کند. یک فیلتر پایین گذر ایده‌آل به مقدار توانی که یک فیلتر پایین گذر از خود عبور می‌دهد، بستگی دارد و در حالت کلی می‌توان گفت فیلتری است که دامنه پاسخ فرکانسی مربعی شکلی دارد و باند عبور آن مطابق با شکل زیر است.

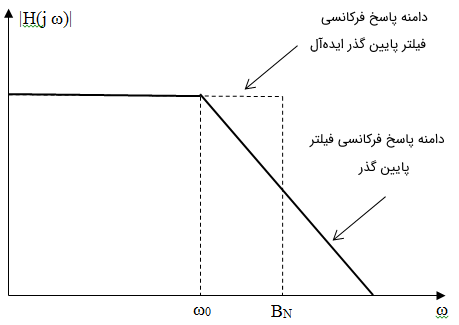
پهنای باند $$B _ N$$ متعلق به فیلتر ایده‌آل، همان پهنای باند معادل نویز است.

به این نکته باید توجه کرد که با افزایش فرکانس قطع فیلتر پایین گذر، پهنای باند $$B _ N$$ نیز افزایش می‌یابد. به همین دلیل گاهی از نسبت $$\frac { B _ N } { \omega _ 0 }$$ به جای $$B _ N$$ استفاده می‌کنیم. در فیلترهای پاسخ ضربه محدود یا FIR با طول‌های بزرگ‌تر و یا فرکانس‌های قطع بالاتر یا در فیلترهای پاسخ ضربه نامحدود یا IIR با مرتبه بالاتر، این نسبت شروع به کاهش می‌کند.

می‌دانیم که در فیلترهای عملی، فرکانس قطع $$\omega _ 0$$ به صورت دقیق وجود ندارد. به عبارت دیگر، هیچ فرکانس مشخصی وجود ندارد که دقیقا در آن فرکانس نمودار پاسخ فرکانسی از یک خط مسطح افقی به یک خط شیب‌دار نزولی تغییر پیدا کند. اما معمولا $$\omega _ 0$$ به عنوان فرکانسی انتخاب می‌شود که پاسخ فرکانسی فیلتر به 3- دسیبل می‌رسد. به عنوان مثال، تابع انتقال ساده‌ترین «فیلتر باترورث» (Butterworth) مرتبه اول به صورت زیر نوشته می‌شود:

$$H ( s ) = \frac { 1 } { 1 + \frac { s } { \omega _ c } } = \frac { 1 } { 1 + j \frac { \omega } { \omega _ c } }$$

در رابطه فوق، $$\omega _ c$$ برابر با فرکانس قطع فیلتر است. اندازه پاسخ فرکانسی فیلتر به صورت زیر در نظر گرفته می‌شود:

$$| H ( j \omega ) | = \frac { \omega _ c } { \sqrt { \omega _ c ^ 2 + \omega ^ 2 } }$$

به دلیل اینکه پاسخ فرکانسی فیلتر باترورث به صورت یکنواخت کاهش می‌یابد، در نتیجه $$H _ { max } = H ( 0 ) = 1$$ است. پهنای باند معادل نویز در این فیلتر به صورت زیر نوشته می‌شود:

$$B _ N = \frac { 1 } { 2 \pi } \int _ 0 ^ { \infty } \frac { \omega _c ^ 2 } { \omega _ c ^ 2 + \omega ^ 2 } \, d \omega = \frac { \pi }{ 2 } \frac { \omega _ c } { 2 \pi } \approx 1 . 57 \frac { \omega _c } { 2 \pi }$$

بنابراین ENBW با فرکانس قطع نرمالیزه شده متناسب است. به یاد داشته باشد که پاسخ فرکانسی در فرکانس قطع برابر است با:

$$| H ( j \omega ) | = \frac { \omega _ c }{ \sqrt { \omega _ c ^ 2 + \omega _ c ^ 2 } } = \frac { 1 } { \sqrt { 2 } } \approx - 3 d b$$

بنابراین پهنای باند معادل نویز برای فرکانس 3- دسیبل برابر با ۱٫۵۷ است.

پهنای باند معادل نویز برای پنجره‌ها

یک پنجره $$W ( K )$$ را در فضای گسسته با زمان تعریف می‌کنیم و آن را به یک فیلتر با پاسخ ضربه FIR محدود اعمال می‌کنیم. اگر ما با این پنجره به عنوان یک فیلتر رفتار کنیم، آن‌گاه پهنای باند معادل آن به صورت زیر به دست می‌آید:

$$B _ N = \sum _ { n = 0 } ^ N | \frac { H ( \omega _ n ) }{ H _ { m a x } } | ^ 2$$

حال با استفاده از «رابطه پارسوال» (Parseval's Theorem) می‌توان نوشت:

$$B _ N = \frac { 1 } { | H _ { m a x } | ^ 2 } \sum _ { n = 0 } ^ { N - 1 } | H ( \omega _ n ) | ^ 2 = \frac { N } { | H _ { m a x } |^ 2 } \sum _ { k = 0 } ^ { N - 1 } | w ( k ) | ^ 2$$

برای یک پنجره معمولی، $$H _ { m a x }$$ در $$\omega =0$$ اتفاق می‌افتد و مولفه صفر تبدیل فوریه گسسته است:

$$| H _ { m a x } | ^ 2 = ( \sum _ { k = 0 } ^ { N - 1 } w ( k ) ) ^ 2$$

بنابراین پهنای باند معادل نویز در یک پنجره معمولی به صورت زیر به دست می‌آید:

$$B _ N = \frac { N \sum _ { k = 0 } ^ { N - 1 } | w ( k ) | ^ 2 }{ ( \sum _ { k = 0 } ^ { N - 1 } w ( k ) ) ^ 2 }$$

به عنوان مثال در یک پنجره مستطیلی، رابطه فوق را می‌توان به صورت زیر ساده‌تر کرد:

$$B _ N = \frac { N N } { N ^ 2 } = 1$$

برای سایر انواع متداول پنجره‌ها، $$B _ N > 1$$ است. می‌توانیم با پنجره مانند یک فیلتر رفتار کنیم. در این صورت پاسخ فرکانسی «پنجره همینگ»‌ (Hamming Window) در تصویر زیر نشان داده شده است.

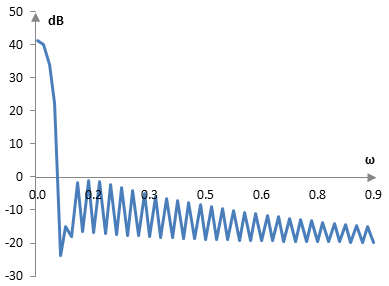
تصویر بالا پاسخ فرکانسی مربوط به یک پنجره با طول 201 نقطه است. این نمودار بخشی از طیف فرکانسی از ۰ تا $$\pi$$ را پوشش داده است. مقدار پیک پنجره در ۱ قرار دارد و مقیاس نشده است تا اطمینان حاصل شود که زمانی که به عنوان فیلتر مورد استفاده قرار می‌گیرد منجر به پاسخ فرکانسی از ۰ تا ۱ می‌شود.

پهنای باند معادل این پنجره برابر با $$B _ N = 1.37$$ است. توجه کنید که در پنجره‌های همینگ با طول بزرگ‌تر، پهنای باند معادل نویز به مقدار ۱٫۳۶ نزدیک می‌شود. یک فیلتر پنجره‌ای برابر با حاصل ضرب $$f ( k ) w ( k )$$ است که $$f ( k )$$ یک فیلتر استاندارد و $$w ( k )$$ یک پنجره است. حال با استفاده از تئوری کانولوشن سیگنال‌ها، تبدیل فوریه حاصل ضرب دو سیگنال برابر با کانولوشن تبدیل فوریه این دو سیگنال است. در نتیجه داریم:

$$F ( f \, w ) = F ( f ) * F ( w )$$

بنابراین پاسخ فرکانسی یک پنجره مانند یک فیلتر روی پاسخ فرکانسی فیلتر قبل از پنجره عمل می‌کند. برای پنجره‌های معمولی، هرچه مقدار $$B _ N$$ کوچک‌تر باشد، دامنه پاسخ فرکانسی نیز یک شیب کاهشی تندتر را از $$| H ( 0 ) |$$ به لوب‌های جانبی خواهد داشت. این امر بدین معنی است که پاسخ فرکانسی یک پنجره معمولی بیشتر و بیشتر به یک سیگنال ضربه شبیه می‌شود. تاثیر پاسخ فرکانسی یک پنجره (فیلتر در کانولوشن بالا) روی پاسخ فرکانسی یک فیلتر استاندارد مانند یک «فیلتر تمام گذر» (All Pass Filter) است.

یک فیلتر تمام گذر دارای پاسخ ضربه محدود FIR استاندارد برابر با یک ضربه است. هر چه پهنای باند معادل نویز کوچک‌تر باشد، پنجره به یک پنجره مستطیلی نزدیک‌تر خواهد بود. به عنوان مثال، «پنجره توکی» (Tukey Window)، با بزرگ‌تر شدن پارامتر پنجره $$\alpha$$ پنجره مستطیلی را تقریب می‌زند. هر چه مقدار پارامتر $$\alpha$$ بزرگ‌تر شود، پهنای باند معادل نویز پنجره توکی به یک نزدیک‌تر می‌شود.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌‌های مهندسی الکترونیک
• آموزش مبانی ​الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
• نسبت سیگنال به نویز چیست؟ — از صفر تا صد
• مدولاسیون چیست؟ — راهنمای جامع
• نمای لیاپانوف (Lyapunov Exponent) چیست؟ — از صفر تا صد

^^