تابع دلتای دیراک — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

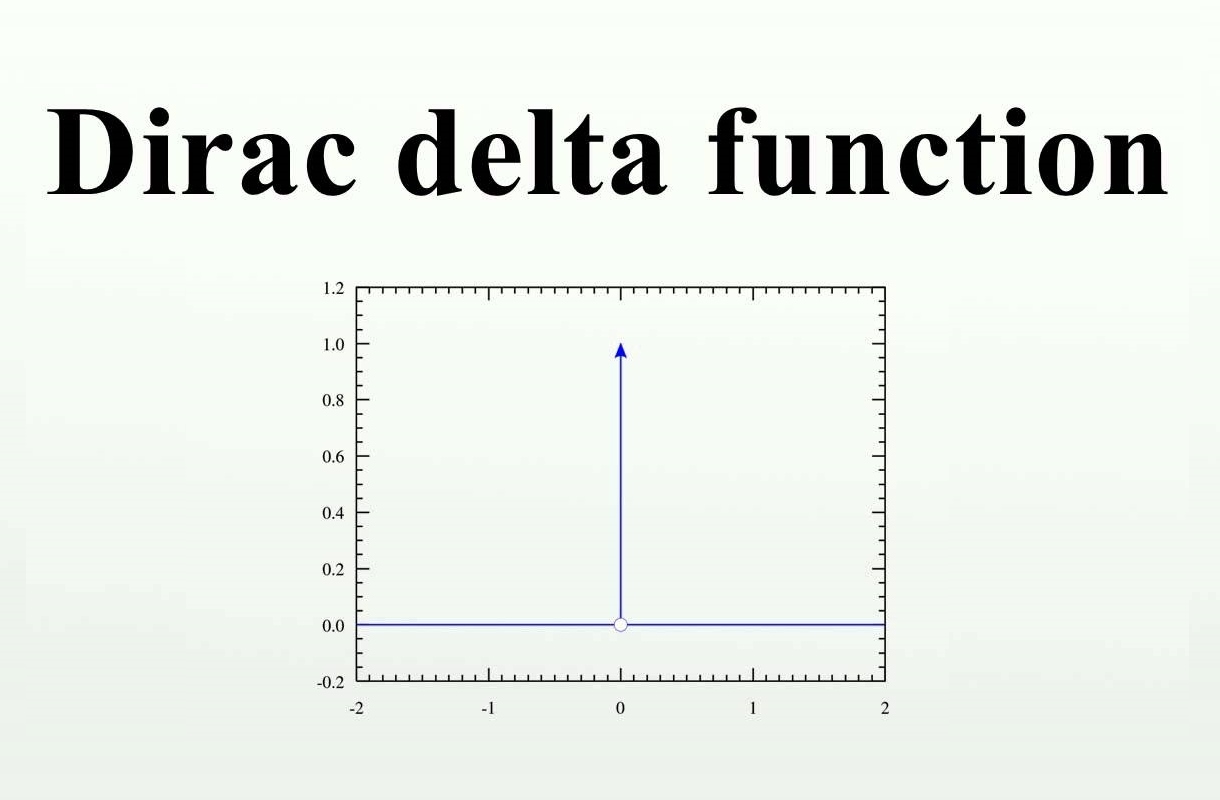
تابع دلتای دیراک، یکی از انواع مختلف توابع تعمیم‌ یافته است که در زمینه‌های مختلف علوم و مهندسی کاربرد فراوانی دارد. برای مثال، اگر بخواهیم یه نیروی بزرگ ناگهانی در زمان کوتاه را به صورت ریاضی بیان کنیم، از این تابع استفاده می‌کنیم. این تابع که تابع ضربه نیز نامیده می‌شود، توسط «پل دیراک» (Paul Dirac) مطرح شد. در ادامه، با این تابع آشنا خواهیم شد.

تابع دلتای دیراک

تاکنون، تعریف‌های زیادی برای تابع دلتای دیراک ارائه شده است. این تابع، سه ویژگی اصلی دارد که دانستن آن‌ها ضروری است. این ویژگی‌ها عبارتند از:

$$\large \delta \left ( { t - a } \right ) = 0 , \, \, \, \, t \ne a$$

فیلم آموزش ریاضی فیزیک 1 + مفاهیم کلیدی در فرادرس

کلیک کنید

$$\large \displaystyle \int _ { { \, a - \varepsilon } } ^ { { \, a + \varepsilon } } { { \delta \left ( { t - a } \right ) \, d t } } = 1 , \hspace {0.25in} \varepsilon > 0$$

$$\large \displaystyle \int _ { { \, \, a - \varepsilon } } ^ { { \, \, a + \varepsilon } } { { f \left ( t \right ) \delta \left ( { t - a } \right ) \, d t } } = f \left ( a \right ) , \hspace {0.25in} \, \, \, \, \, \, \, \, \, \varepsilon > 0$$

در $$t=a$$، مقدار تابع دلتای دیراک، بی‌نهایت است. بنابراین، مقدار تابع دلتای دیراک، جز در یک نقطه که برای آن تعریف شده است، بی‌نهایت یا تعریف‌ نشده است. لازم به ذکر است که انتگرال در ویژگی‌های دوم و سوم، برای هر بازه شامل نقطه $$t = a$$ درست است.

تابع دلتای دیراک، تابع جالبی است. مقدار این تابع، در هر جایی جز یک نقطه، صفر است و مقدار انتگرال آن در هر بازه‌ای که آن نقطه را شامل شود، برابر با ۱ است. اگر کمی دقت کنیم، می‌بینیم که تابع دلتای دیراک یک تابع واقعی نیست و در حقیقت،‌ مثالی از چیزی است که «تابع تعمیم یافته» (Generalized Function) یا «توزیع تعمیم‌ یافته» (Generalized Distribution) نامیده می‌شود. با وجود عجیب بودن، این «تابع» در مدل‌سازی شوک‌های ناگهانی و یا نیروهای بزرگ به یک سیستم بسیار کارآمد است.

فرض کنید می‌خواهیم یک دیفرانسیل شامل تابع دلتای دیراک را حل کنیم. قبل از حل مسئله مقدار اولیه، لازم است تابع دلتای دیراک را تبدیل کنیم. برای این کار می‌توانیم از ویژگی سوم استفاده کنیم.

$$ \large \mathcal { L } \left \{ { \delta \left ( { t - a } \right ) } \right\} = \int _ { { \, 0 } } ^ { \infty } { { { { \bf { e } } ^ { - s \, t } } \delta \left ( { t - a } \right ) \, d t } } = { { \bf { e } } ^ { - a \, s } } \hspace {0.25in} \hspace {0.25in} { \mbox { } } a > 0 $$

توجه کنید که ویژگی‌های دوم و سوم، اغلب از منفی بی‌نهایت تا بی‌نهایت تعریف می‌شوند. اما برای هر بازه‌ای که شامل $$t=a$$ باشد، برقرار هستند.

اکنون می‌توانیم یک مسئله مقدار اولیه شامل تابع دلتای دیراک را حل کنیم.

مثال ۱

مسئله مقدار اولیه زیر را حل کنید.

$$\large y ^ { \prime \prime } + 2 y ^ \prime - 1 5 y = 6 \delta \left ( { t - 9 } \right ) , \hspace{0.25in} \hspace {0.25in} y \left ( 0 \right ) = - 5 \, \, \, \, \, \, y ^ \prime \left ( 0 \right ) = 7$$

حل: با گرفتن تبدیل لاپلاس و اعمال شرایط اولیه، داریم:

$$\large \begin {align*} { s ^ 2 } Y \left ( s \right ) - s y \left ( 0 \right ) - y ^ \prime \left ( 0 \right ) + 2 \left ( { s Y \left ( s \right ) - y \left ( 0 \right ) } \right ) - 1 5 Y \left( s \right ) & = 6 { { \bf { e } } ^ { - 9 s } } \\ \left ( { { s ^ 2 } + 2 s - 1 5 } \right ) Y \left ( s \right ) + 5 s + 3 & = 6 { { \bf { e } } ^ { - 9 s } } \end {align*}$$

در نتیجه، مقدار $$Y(s)$$ به صورت زیر خواهد بود:

$$\large \begin {align*} Y \left ( s \right ) & = \frac { { 6 { { \bf { e } } ^ { - 9 s } } } } { { \left ( { s + 5 } \right ) \left ( { s - 3 } \right ) } } - \frac { { 5 s + 3 } } { { \left ( { s + 5 } \right ) \left ( { s - 3 } \right ) } } \\ & = 6 { { \bf { e } } ^ { - 9 s } } F \left ( s \right ) - G \left ( s \right ) \end {align*}$$

اکنون از تجزیه به کسرهای جزئی کمک می‌گیریم:

$$\large \begin {align*} F \left ( s \right ) & = \frac { 1 } { { \left ( { s + 5 } \right ) \left ( { s - 3 } \right ) } } = \frac { { \frac { 1 } { 8 } } } { { s - 3 } } - \frac { { \frac { 1 } { 8 } } } { { s + 5 } } \\ f \left ( t \right ) & = \frac { 1 } { 8 } { { \bf { e } } ^ { 3 t } } - \frac { 1 } { 8 } { { \bf { e } } ^ { - 5 t } } \end {align*}$$

$$\large \begin {align*} G \left ( s \right ) & = \frac { { 5 s + 3 } } { { \left ( { s + 5 } \right ) \left ( { s - 3 } \right ) } } = \frac { { \frac { 9 } { 4 } } } { { s - 3 } } + \frac { { \frac { { 1 1 } } { 4 } } } { { s + 5 } } \\ g \left ( t \right ) & = \frac { 9 } { 4 } { { \bf { e } } ^ { 3 t } } + \frac { { 1 1 } } { 4 }{ { \bf { e } } ^ { - 5 t } } \end {align*}$$

در نتیجه، حل نهایی معادله، به صورت زیر خواهد بود:

$$\large \begin {align*} Y \left ( s \right ) & = 6 { { \bf { e } } ^ { - 9 s } } F \left ( s \right ) - G \left ( s \right ) \\ y \left ( t \right ) & = 6 { u _ 9 } \left ( t \right ) f \left ( { t - 9 } \right ) - g \left ( t \right ) \end {align*}$$

که در آن $$f(t)$$ و $$g(t)$$ در بالا تعریف شدند.

فیلم آموزش الکترومغناطیس 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

مثال ۲

مسئله مقدار اولیه زیر را حل کنید.

$$\large 2 y ^ {\prime \prime } + 1 0 y = 3 { u _ { 1 2 } } \left ( t \right ) - 5 \delta \left ( { t - 4 } \right ) , \hspace {0.25in} \hspace {0.25in} y \left ( 0 \right ) = - 1 \, \, \, \, \, \, y ^ \prime \left ( 0 \right ) = - 2$$

حل: با گرفتن تبدیل لاپلاس و اعمال شرایط اولیه، داریم:

$$\large \begin {align*} 2 \left ( { { s ^ 2 } Y \left ( s \right ) - s y \left ( 0 \right ) - y ^ \prime \left ( 0 \right ) } \right ) + 1 0 Y \left ( s \right ) & = \frac { { 3 { { \bf { e } } ^ { - 1 2 s } } } } { s } - 5 { { \bf { e } } ^ { - 4 s } } \\ \left ( { 2 { s ^ 2 } + 1 0 } \right ) Y \left ( s \right ) + 2 s + 4 & = \frac { { 3 { { \bf { e } } ^ { - 1 2 s } } } } { s} - 5 { { \bf { e } } ^ { - 4 s } } \end {align*}$$

در نتیجه، مقدار $$Y(s)$$ به صورت زیر خواهد بود:

$$\large \begin {align*} Y \left ( s \right) & = \frac { { 3 { { \bf { e } } ^ { - 1 2 s } } } } { { s \left ( { 2 { s ^ 2 } + 1 0 } \right ) } } - \frac { { 5 { { \bf { e } } ^ { - 4 s } } } } { { 2 { s ^ 2 } + 1 0 } } - \frac { { 2 s + 4 } } { { 2 { s ^ 2 } + 1 0 } } \\ & = 3 { { \bf { e } } ^ { - 1 2 s } } F \left ( s \right ) - 5 { { \bf { e } } ^ { - 4 s } } G \left ( s \right ) - H \left ( s \right ) \end {align*}$$

لازم است تابع نخست عبارت بالا را به کسرهای جزئی تجزیه کنیم:

$$\large \begin {align*} F \left ( s \right ) & = \frac { 1 } { { s \left ( { 2 { s ^ 2 } + 1 0 } \right ) } } = \frac { 1 } { { 1 0 } } \frac { 1 } { s } - \frac { 1 } { { 1 0 } } \frac { s } { { { s ^ 2 } + 5 } } \\ f \left ( t \right ) & = \frac { 1 } { { 1 0 } } - \frac { 1 } { { 1 0 } } \cos \left ( { \sqrt 5 \, t } \right ) \end {align*}$$

عکس تبدیل لاپلاس سایر جملات نیز به صورت است:

$$\large g \left ( t \right ) = \frac { 1 } { { 2 \sqrt 5 } } \sin \left ( { \sqrt 5 \, t } \right )$$

$$\large h \left ( t \right ) = \cos \left ( { \sqrt 5 \, t } \right ) + \frac { 2 } { { \sqrt 5 } } \sin \left ( { \sqrt 5 \, t } \right )$$

در نتیجه، حل نهایی معادله، به صورت زیر خواهد بود:

$$\large \begin {align*} Y \left ( s \right ) & = 3 { { \bf { e } } ^ { - 1 2 s } } F \left ( s \right ) - 5 { { \bf { e } } ^ { - 4 s } } G \left ( s \right ) - H \left ( s \right ) \\ y \left ( t \right ) & = 3 { u _ { 1 2 } } \left ( t \right ) f \left ( { t - 1 2 } \right ) - 5 { u _ 4 } \left ( t \right ) g \left ( { t - 4 } \right ) - h \left ( t \right ) \end {align*}$$

که در آن $$f(t)$$، $$g(t)$$ و $$h(t)$$ در بالا تعریف شدند.

در این‌جا می‌خواهیم ارتباط تابع پله و تابع دلتای دیراک را به دست آوریم. ابتدا انتگرال زیر را در نظر بگیرید:

$$ \large \int _ { { \, - \infty } } ^ { t } { { \delta \left ( { u - a } \right ) \, d u } } = \left\{ { \begin {array} { * { 2 0 } { l } } 0, &{ \hspace {0.25in} { \mbox { }}t < a}\\ 1, & { \hspace {0.25in} { \mbox { } } t > a } \end {array} } \right . $$

همان‌گونه که می‌بینیم، حاصل انتگرال دقیقاً همان تعریف تابع پله است. بنابراین، می‌توان نوشت:

$$\large \int _ { { \, - \infty } } ^ { t } { { \delta \left ( { u - a } \right ) \, d u } } = { u _ a } \left ( t \right )$$

و با استفاده از قضیه اساسی حسابان، داریم:

$$\large {u'_a}\left( t \right) = \frac{d}{{dt}}\left( {\int_{{\, - \infty }}^{t}{{\delta \left( {u - a} \right)\,du}}} \right) = \delta \left( {t - a} \right)$$

در نتیجه، می‌توان گفت که مشتق تابع پله، برابر با تابع دلتای دیراک است.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تقلب نامه (Cheat Sheet) معادلات دیفرانسیل
• انتگرال کانولوشن — به زبان ساده
• تبدیل z — به زبان ساده

^^