کانولوشن در متلب — از صفر تا صد

کانولوشن (Convolution) یک عملگر ریاضی است که برای بیان رابطه بین ورودی و خروجی یک سیستم خطی تغییر ناپذیر با زمان یا LTI مورد استفاده قرار می‌گیرد. در این مطلب می‌خواهیم نحوه محاسبه کانولوشن دو سیگنال و خواص کانولوشن را بررسی کنیم. سپس کانولوشن دو سیگنال در متلب را محاسبه می‌کنیم و در نهایت به بررسی کاربرد و مفهوم کانولوشن در علوم مختلف مانند شبکه‌های عصبی مصنوعی می‌پردازیم.

بیان ریاضی کانولوشن

با استفاده از کانولوشن می‌توان ورودی، پاسخ ضربه (Impulse Response) و خروجی یک سیستم را به یکدیگر مرتبط کرد.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

این کار بر اساس فرمول زیر صورت می‌گیرد:

$$y (t) = x(t) * h(t)$$

در فرمول بالا، $$y(t)$$ خروجی یک سیستم LTI و $$h(t)$$ پاسخ ضربه آن سیستم و $$x(t)$$ ورودی سیستم LTI است. در حالت کلی دو نوع کانولوشن وجود دارد:

1. کانولوشن پیوسته
2. کانولوشن گسسته

کانولوشن پیوسته

در شکل زیر می‌توان بلوک دیاگرامی از رابطه ورودی، پاسخ ضربه و خروجی یک سیستم LTI پیوسته با زمان را مشاهده کرد:

برای این سیستم، می‌توان رابطه زیر را نوشت:

$$y(t) \,\,= x (t) * h (t) \\ = \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$$

این فرمول را می‌توان به صورت زیر نیز بازنویسی کرد:

$$y(t) = \int_{-\infty}^{\infty} x(t - \tau) h (\tau)d\tau$$

رابطه بالا نحوه محاسبه کانولوشن بین دو سیگنال ورودی و پاسخ ضربه سیستم پیوسته در زمان را نشان می‌دهد. با استفاده از این عبارت می‌توان خروجی یک سیستم را به دست آورد.

کانولوشن گسسته

در تصویر زیر، بلوک دیاگرام یک سیستم LTI با سیگنال‌های گسسته در زمان نشان داده شده است.

برای این سیستم نیز مجددا رابطه زیر برقرار است:

$$y(n)\,\,= x (n) * h (n)$$

$$= \Sigma_{k = - \infty}^{\infty} x(k) h (n-k)$$

رابطه بالا به صورت دیگری نیز نوشته می‌شود:

$$y(n) = = \Sigma_{k = - \infty}^{\infty} x(n-k) h (k)$$

توجه کنید که با استفاده از کانولوشن می‌توان پاسخ حالت صفر یک سیستم را به دست آورد. عکس فرایند کانولوشن، دکانولوشن (Deconvolution) نام دارد که به صورت گسترده در پردازش سیگنال و پردازش تصویر مورد استفاده قرار می‌گیرد.

خواص کانولوشن

کانولوشن دارای خاصیت‌های (Properties) فراوانی است که می‌توان برای محاسبه راحت‌تر کانولوشن دو سیگنال از آن‌ها بهره برد. به صورت خلاصه می‌توان گفت کانولوشن دارای خواص زیر است.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

خاصیت جا‌به‌جایی

خاصیت جابه‌جایی (Commutative Property) کانولوشن دو سیگنال به صورت زیر بیان می‌شود:

$$x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t)$$

خاصیت توزیع‌پذیری

برای بیان خاصیت توزیع‌پذیری (Distributive Property) به عنوان مثال در مورد کانولوشن سه سیگنال می‌توان نوشت:

$$x_1 (t) * [x_2 (t) + x_3 (t) ] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$$

خاصیت شرکت‌پذیری

خاصیت شرکت‌پذیری (Associative Property) سیگنال‌ها در کانولوشن به صورت زیر است:

$$x_1 (t) * [x_2 (t) * x_3 (t) ] = [x_1 (t) * x_2 (t)] * x_3 (t)$$

خاصیت انتقال

کانولوشن همچنین دارای خاصیت انتقال (Shifting Property) است که به صورت زیر می‌توان آن را بیان کرد:

$$x_1 (t) * x_2 (t) = y (t)$$

$$x_1 (t) * x_2 (t-t_0) = y (t-t_0)$$

$$x_1 (t-t_0) * x_2 (t) = y (t-t_0)$$

$$x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1)$$

کانولوشن با تابع ضربه

کانولوشن یک سیگنال با سیگنال ضربه برابر است با:

$$x_1 (t) * \delta (t) = x(t)$$

$$x_1 (t) * \delta (t- t_0) = x(t-t_0)$$

کانولوشن پله واحد

برای محاسبه کانولوشن یک تابع پله واحد (Unit Step) با تابع پله واحد دیگر می‌توان به صورت زیر عمل کرد:

$$u (t) * u (t) = r(t)$$

$$u (t-T_1) * u (t-T_2) = r(t-T_1-T_2)$$

$$u (n) * u (n) = [n+1] u(n)$$

خاصیت تغییر مقیاس

خاصیت تغییر مقیاس (Scaling Property) در کانولوشن به صورت زیر است. اگر داشته باشیم:

$$x (t) * h (t) = y (t)$$

آن‌گاه می‌توان نوشت:

$$x (a t) * h (a t) = {1 \over |a|} y (a t)$$

مشتق خروجی

اگر در یک سیستم رابطه زیر برقرار باشد:

$$y (t) = x (t) * h (t)$$

آن‌گاه با اعمال مشتق روی خروجی، دو رابطه زیر برقرار خواهند بود:

$${dy (t) \over dt} = {dx(t) \over dt} * h (t)$$

$${dy (t) \over dt} = x (t) * {dh(t) \over dt}$$

همچنین خواص زیر در مورد کانولوشن سیگنال‌ها برقرار است:

• کانولوشن دو سیگنال علّی (Causal)، یک سیگنال علّی خواهد بود.
• کانولوشن دو سیگنال غیرعلّی، سیگنالی غیرعلّی خواهد بود.
• از کانولوشن دو سیگنال مستطیلی شکل با طول نابرابر، یک سیگنال ذوزنقه‌ای شکل به دست می‌آید.
• از کانولوشن دو سیگنال مستطیلی با طول برابر، یک سیگنال مثلثی شکل به دست می‌آید.
• اگر یک تابع با تابع پله کانولوشن شود، حاصل برابر با انتگرال آن تابع خواهد بود.

به عنوان مثال، برای محاسبه کانولوشن زیر:

$$u(t) * u(t) = r(t)$$

از روی خواص بالا می‌توان نوشت:

$$u(t) * u(t) = \int u(t)dt = \int 1dt = t = r(t)$$

در این حالت، نتیجه با استفاده از انتگرال $$u(t)$$ به دست می‌آید.

بازه کانولوشن

اگر دو سیگنال با یکدیگر کانولوشن شوند، آن‌گاه بازه سیگنال حاصل از کانولوشن‌ به صورت زیر به دست می‌آید:

• بازه سیگنال حاصل از کانولوشن ($$t$$)، بزرگ‌تر از مجموع کران‌های پایین و کوچک‌تر از مجموع کران‌های بالای دو سیگنال خواهد بود.

به عنوان مثال، بازه سیگنال حاصل از کانولوشن دو تابع تصویر زیر را می‌خواهیم به دست آوریم.

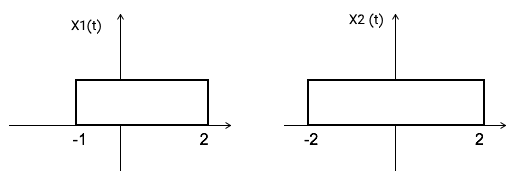
در این تصویر، دو سیگنال مستطیلی شکل را می‌خواهیم با یکدیگر کانولوشن کنیم که دارای طول متفاوت هستند. در نتیجه، سیگنال حاصل یک پالس ذوزنقه‌ای خواهد بود. بازه این سیگنال ذوزنقه‌ای شکل را با استفاده از قانون فوق می‌توان به دست آورد:

$$-1+-2 < t < 2+2$$

$$-3 < t < 4$$

بنابراین قاعده ذوزنقه برابر با ۷ به دست می‌آید.

مساحت سیگنال کانولوشن

مساحت زیر سیگنال کانولوشن را می‌توان به صورت زیر به دست آورد:

$$A_y = A_x A_h$$

در این فرمول، $$A_x$$ برابر با مساحت زیر سیگنال ورودی، $$A_h$$ مساحت زیر سیگنال پاسخ ضربه و $$A_y$$ برابر با مساحت زیر سیگنال خروجی است.

اثبات:

می‌دانیم که کانولوشن دو سیگنال برابر است با:

$$y(t) = \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$$

با گرفتن انتگرال از هر دو سمت معادله داریم:

$$\int y(t)dt \,\,\, =\int \int_{-\infty}^{\infty}\, x (\tau) h (t-\tau)d\tau dt$$

$$=\int x (\tau) d\tau \int_{-\infty}^{\infty}\, h (t-\tau) dt$$

می‌دانیم که سطح زیر هر منحنی برابر با انتگرال آن منحنی است. بنابراین می‌توان نوشت:

$$\therefore A_y = A_x\,A_h$$

مولفه DC

مولفه DC هر سیگنالی را می‌توان با استفاده از تقسیم سطح زیر سیگنال بر دوره تناوب سیگنال به دست آورد.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

مثال

مولفه DC سیگنال حاصل از کانولوشن دو تابع زیر را به دست آوردید.

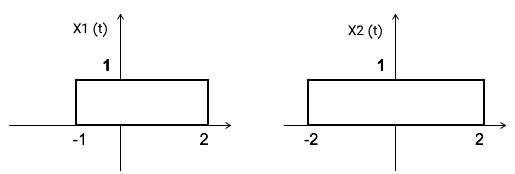
حل:

بر اساس تصویر بالا، سطح زیر نمودار $$X_1$$ برابر با $$1 \times 3 = 3$$ و سطح زیر نمودار $$X_2$$ برابر با $$1 \times 4 = 4$$ است. از نتایج بخش قبل می‌دانیم که سطح زیر سیگنال حاصل از کانولوشن، از ضرب مساحت دو سیگنال بالا و برابر با $$3\times 4 =12$$ به دست می‌آید. بازه سیگنال کانولوشن را نیز می‌توان با اطلاعات بخش‌‌های قبل به صورت زیر محاسبه کرد:

$$-1 + -2 < t < 2 + 2$$

$$-3 < t < 4$$

بنابراین بازه تناوب این سیگنال برابر با ۷ خواهد بود. حال مولفه DC سیگنال را از تقسیم سطح زیر سیگنال بر بازه تناوب سیگنال برابر با $$\frac {12} {7}$$ به دست می‌آوریم.

کانولوشن گسسته

در این بخش می‌خواهیم به نحوه محاسبه کانولوشن دو سیگنال گسسته در زمان بپردازیم. فرمول کانولوشن گسسته در زمان را در بخش‌های قبل ذکر کردیم. در این بخش کانولوشن دو نوع از سیگنال‌های گسسته را نشان می‌دهیم.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

محاسبه کانولوشن گسسته خطی

فرض کنید که می‌خواهیم کانولوشن دو دنباله گسسته $$x[n] = [a, b, c]$$ و $$h[n] = [e, f, g]$$ را به دست آوریم. برای این کار، می‌توانیم مقادیر را به صورت تصویر زیر در جدولی وارد کنیم.

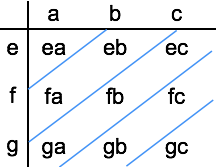
سپس جدول را مطابق شکل با خطوط مورب گروه‌بندی کرده و داده‌هایی که در یک گروه قرار می‌گیرند را با یکدیگر جمع کنیم. در نهایت داده‌ها را از قطر بالا سمت چپ تا قطر پایین سمت راست به ترتیب بنویسم. این دنباله اعداد حاصل از کانولوشن بین دو دنباله داده گسسته است.

توجه کنید که اگر دو دنباله به ترتیب دارای m و n تعداد نمونه باشند، آن گاه دنباله کانولوشن حاصل دارای m+n-1 نمونه خواهد بود.

مثال

کانولوشن دو دنباله عددی $$x[n] = [1, 2, 3]$$ و $$h[n] = [-1, 2, 2]$$ را محاسبه کنید.

حل:

ابتدا داده‌ها را در جدول زیر وارد می‌کنیم.

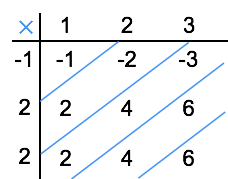
سپس کانولوشن را از روی جدول محاسبه می‌کنیم. خروجی به صورت $$y[n] = [-1, -2+2, -3+4+2, 6+4, 6] = [-1, 0, 3, 10, 6]$$ به دست می‌آید.

در این مثال، دنباله $$x[n]$$ دارای ۳ نمونه و دنباله $$h[n]$$ نیز دارای ۳ نمونه هستند، در نتیجه دنباله حاصل دارای $$3+3-1=5$$ نمونه است.

محاسبه کانولوشن متناوب یا دایره‌ای

کانولوشن متناوب یا دایره‌ای برای تبدیل فوریه گسسته معتبر است. برای محاسبه کانولوشن دایره‌ای، تمام نمونه‌ها باید حقیقی باشند. کانولوشن پریودیک یا متناوب به عنوان کانولوشن سریع نیز شناخته می‌شود. اگر دو دنباله با طول‌های m و n با یکدیگر کانولوشن سریع شوند، آن‌گاه دنباله حاصل دارای طول $$max [m,n]$$ خواهد بود.

مثال

کانولوشن سریع دو دنباله $$x[n] = [1, 2, 3]$$ و $$h[n] = [-1, 2, 2]$$ را به دست آورید.

حل

مجددا داده‌ها را در جدول زیر وارد می‌کنیم.

همان طور که در بخش قبل محاسبه کردیم، کانولوشن دو سیگنال گسسته در زمان به صورت زیر محاسبه می‌شود:

$$y[n] = [-1, -2+2, -3+4+2, 6+4, 6] = [-1, 0, 3, 10, 6]$$

برای محاسبه کانولوشن دایره‌ای دو سیگنال، ابتدا طول سیگنال خروجی آن را به دست می‌آوریم. طول دنباله اول برابر با ۳ و طول دنباله دوم نیز ۳ است. بنابراین طول دنباله کانولوشن متناوب حاصل برابر با $$max [3,3] = 3$$ خواهد بود.

حال چون تناوب برابر با ۳ به دست آمده است، در نتیجه ۳ داده اول از دنباله خروجی را مطابق با تصویر زیر با دو داده دیگر جمع می‌کنیم.

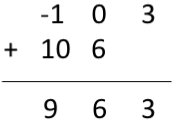
در نهایت حاصل کانولوشن متناوب به صورت $$y[n] = [9, 6, 3]$$ به دست می‌آید.

همبستگی و کانولوشن

همبستگی (Correlation) یک معیار آماری برای اندازه‌گیری مشابهت (Similarity) بین دو سیگنال است. فرمول کلی برای محاسبه همبستگی بین دو سیگنال به صورت زیر است:

$$\int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau) dt$$

با دقت در فرمول بالا متوجه می‌شوید که بین این فرمول و رابطه کانولوشن شباهت بسیار زیادی وجود دارد. به همین دلیل بهتر است مبحث همبستگی نیز در این مطلب بیان شود. دو نوع همبستگی برای محاسبه شباهت بین دو سیگنال وجود دارند:

• تابع خودهمبستگی (Auto Correlation)
• تابع همبستگی متقابل (Cros Correlation)

تابع خودهمبستگی

تابع خودهمبستگی به عنوان همبستگی یا شباهت یک سیگنال با خودش تعریف می‌شود. در واقع این تابع، معیاری برای اندازه‌گیری شباهت یک سیگنال و نسخه دارای تاخیر زمانی آن به حساب می‌آید. تابع خودهمبستگی را با نماد $$R(\tau)$$ نشان می‌دهند.

فیلم آموزش ریاضی مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

یک سیگنال $$x(t)$$ را در نظر بگیرید. تابع خودهمبستگی برای این سیگنال و تابع تاخیر زمانی آن به صورت زیر نوشته می‌شود:

$$R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x(t-\tau) dt \quad \quad \text{[+ve shift]}$$

$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t)x(t + \tau) dt \quad \quad \text{[-ve shift]}$$

در رابطه بالا، $$\tau$$ پارامتر تاخیر یا اسکن نامیده می‌شود. اگر سیگنال مختلط باشد، آن‌گاه تابع خودهمبستگی توسط رابطه زیر به دست می‌آید:

$$R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x * (t-\tau) dt \quad \quad \text{[+ve shift]}$$

$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t + \tau)x * (t) dt \quad \quad \text{[-ve shift]}$$

خواص تابع خودهمبستگی سیگنال انرژی

• تابع خودهمبستگی متقارن مزدوج است. در نتیجه، رابطه زیر برای این تابع برقرار است:

$$R(\tau) = R^*(-\tau)$$

• تابع خودهمبستگی برای یک سیگنال انرژی در مبدا یا $$\tau =0$$، برابر با مجموع انرژی سیگنال است.

$$R(0) = E = \int_{-\infty}^{\infty}\,|\,x(t)\,|^2\,dt$$

• تابع خودهمبستگی سیگنال با معکوس پارامتر تاخیر ($$\frac {1} {\tau}$$) متناسب است.
• تبدیل فوریه تابع خودهمبستگی متناظر با تابع چگالی طیف انرژی (Energy Spectral Densities) یک سیگنال است.

$$F.T\,[ R (\tau) ] = \Psi(\omega)$$

$$\Psi(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d \tau$$

• برای محاسبه تابع خودهمبستگی می‌توان به صورت زیر عمل کرد.

$$R (\tau) = x (\tau)* x(-\tau)$$

تابع خودهمبستگی سیگنال توان

تابع خودهمبستگی برای یک سیگنال توان (Power Signal) متناوب با دوره تناوب T به صورت زیر به دست می‌آید:

$$R (\tau) = \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x* (t-\tau) dt$$

این تابع دارای خواص زیر است:

• تابع خودهمبستگی سیگنال توان دارای خاصیت متقارن مزدوج است.

$$R (\tau) = R^*(-\tau)$$

• تابع خودهمبستگی یک سیگنال توان در مبدا یا $$\tau =0$$ برابر با توان کل یک سیگنال است.

$$R (0)= \rho$$

• تابع خودهمبستگی سیگنال توان با معکوس پارامتر تاخیر ($$\frac {1} {\tau}$$) متناسب است.
• تابع خودهمبستگی سیگنال توان در مبدا یا $$\tau =0$$ بیشینه می‌شود.

$$| R (\tau) | \leq R (0)\, \forall \,\tau$$

• تابع خودهمبستگی و تابع چگالی طیف توان یک سیگنال، متناظر با تبدیل فوریه سیگنال هستند.

$$F.T[ R (\tau) ] = s(\omega)$$

$$s(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d\tau$$

• در محاسبه تابع خودهمبستگی یک سیگنال توان، رابطه زیر برقرار است:

$$R (\tau) = x (\tau)* x(-\tau)$$

شباهت بین کانولوشن و تابع همبستگی

اگر به فرمول‌های توابع خودهمبستگی و همبستگی متقابل توجه کرده باشید، متوجه می‌شوید که شباهت بسیار زیادی بین این توابع و کانولوشن دو سیگنال وجود دارد. در واقع تابع به دست آمده با استفاده از کانولوشن، دقیقا قرینه تابع همبستگی متقابل است. این موضوع در تصویر زیر به خوبی نشان داده شده است.

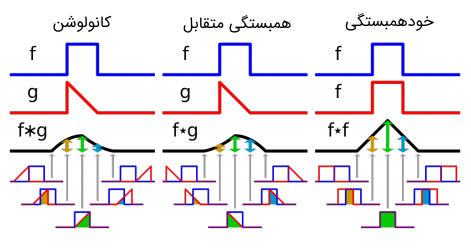
کانولوشن دو سیگنال در متلب

در این قسمت می‌خواهیم نحوه محاسبه کانولوشن دو تابع در نرم‌افزار متلب را بررسی کنیم. در نرم‌افزار متلب از دستور $$y = conv(x, h)$$ برای محاسبه کانولوشن دو دنباله $$x(n)$$ و $$h(n)$$ با طول محدود استفاده می‌شود.

فیلم آموزش آشنایی با پردازش سیگنال های دیجیتال در متلب MATLAB در فرادرس

کلیک کنید

به عنوان مثال، اگر بخواهیم کانولوشن بین دو تابع ضربه یا معادله $$y(n) = \delta (n) * \delta (n-1)$$ را در بازه $$n= {0, 1, 2}$$ به دست آوریم، می‌توانیم از کد زیر استفاده کنیم.

1x1 = [1 0 0];
2x2 = [0 1 0];
3y = conv(x1,x2);
4t = 0:length(y)-1;
5stem(t,y);

همچنین کانولوشن بین دو سیگنال $$x(n)= {-2, 0, 1, -1, 3}$$ و $$h(n)= {1, 2, 0, -1}$$ را با استفاده از کد زیر می‌توان به دست آورد و سپس نتیجه را ترسیم کرد.

1clc , clear all , close all
2x = [-2 0 1 -1 3]; % x(n)
3h = [1 2 0 -1]; % h(n)
4y = conv (x,h); % convolution
5n1 = length (h) -1;
6n2 = length (x) -1;
7k = -n1:1: n2;
8disp ([ ’Output Sequence y[n] = ’, num2str (y)]);
9figure ;
10subplot (311)
11stem(x,’.’), title (’x[n]’)
12subplot (312)
13stem(h,’.’), title (’h[n]’)
14subplot (313)
15stem(k,y ,’.’), title (’y[n]’)

همان طور که گفتیم از کانولوشن برای محاسبه پاسخ یک سیستم LTI استفاده می‌کنیم. همچنین با استفاده از خروجی و ورودی یک سیستم، می‌توان پاسخ ضربه سیستم را نیز به دست آورد. مثلا سیستم زیر را در نظر بگیرید:

$$\begin{array}{r}{y[n]+0.7 y[n-1]-0.45 y[n-2]-0.6 y[n-3]=} \\ {0.8 x[n]-0.44 x[n-1]+0.36 x[n-2]+0.02 x[n-3]}\end{array}$$

با استفاده از کد زیر می‌توان تابع ضربه سیستم را به دست آورد.

1clc , clear all , close all
2p = [0.8 -0.44 0.36 0.02]; % x(n) coefficients
3d = [1 0.7 -0.45 -0.6]; % coefficients of y(n)
4N = 41; % desired impulse response length
5x = [1 zeros (1,N -1) ]; % impulse input
6y = filter (p,d ,x); % impulse response (output )
7k = 0:1:N -1;
8stem(k,y)
9title (’Impulse response ’)
10xlabel (’Time index (n)’)
11ylabel (’Amplitude ’)

همبستگی متقابل بین دو سیگنال $$h(n)= {0.5, 1, 2, 1, 0.5}$$ و $$X(n)= {0, 1, -2, 3, -4}$$ را نیز با استفاده از کد زیر می‌توان محاسبه و ترسیم کرد.

1clc , clear all , close all
2t = [-5 -4 -3 -2 -1 0 1 2 3 4 5]; % x -axis
3x = [ 0 0 0 0 0 0 1 -2 3 -4 0]; % input
4h = [ 0 0 0 0.5 1 2 1 0.5 0 0 0]; % response
5y = xcorr2 (x,h);
6n1 = length (x) -1;
7n2 = length (h) -1;
8k = -n1:1: n2;
9disp ([ ’Output Sequence y[n] = ’, num2str (y)]);
10figure ;
11subplot (311)
12stem(t,x ,’m.’), title (’x[n]’)
13subplot (312)
14stem(t,h ,’r.’), title (’h[n]’)
15subplot (313)
16stem(k,y ,’.’), title (’y[n]’)
17axis ([ -10 10 -7 2])

البته نتایج بالا را با استفاده از قطعه کد زیر نیز می‌توان به دست آورد.

1clc , clear all , close all
2t = [-5 -4 -3 -2 -1 0 1 2 3 4 5]; % x -axis
3x = [ 0 0 0 0 0 0 1 -2 3 -4 0]; % input
4h = [ 0 0 0 0.5 1 2 1 0.5 0 0 0]; % response
5y = [ 0 0 0 0 0 0 0 0 0 0 0];
6yc = 1;
7for n=min (t):max (t),
8pause (3) ;
9% flip h
10ht = fliplr (h);
11if n <0,
12% shift to the left
13ht = [ht(-n+1: length (h)) zeros (1,-n)];
14else
15% shift to the right
16ht = [ zeros (1, n) ht(1: length (h)-n)];
17end
18y(yc) = sum (x.*ht);
19yc = yc + 1;
20subplot (2 ,1 ,1) ;
21stem (t,x);
22hold on;
23stem (t,ht ,’filled ’,’r’);
24hold off ;
25xlabel (’t’);
26legend (’x[n]’,’h[n -k]’ ,0);
27title ([ ’n=’ num2str (n)]);
28subplot (2 ,1 ,2) ;
29stem (t,y);
30xlabel (’t’);
31ylabel (’y[n]’);
32end

برای محاسبه تابع خودهمبستگی سیگنال $$X(n)= {1, 2, 1, 1 }$$ می‌توان از کد زیر استفاده کرد.

1clc , clear all , close all
2x = [1 2 1 1];
3y = xcorr2 (x);
4n = length (x) -1;
5k = -n:1: n;
6disp ([ ’Output Sequence y[n] = ’, num2str (y)]);
7figure ;
8subplot (211)
9stem(x,’.’), title (’x[n]’)
10subplot (212)
11stem(k,y ,’.’)
12title (’y[n]’)
13xlabel (’Lag index k’)
14ylabel (’Amplitude ’)

کاربردهای دیگر کانولوشن

در حوزه یادگیری ماشین (Machine Learning)، عملگر کانولوشن جایگاه بسیار ویژه‌ای را به خود اختصاص داده است. در پردازش سیگنال‌های صوتی، از کانولوشن به عنوان یک صاف‌کننده سیگنال یاد می‌شود. در شبکه‌های کانولوشنی و یادگیری عمیق، کانولوشن قادر است اطلاعات را از پیکسل‌های اطراف جمع‌آوری کند و همچنین به عنوان یک فیلتر تطبیق الگو (Pattern Matching Filter) عمل می‌کند که در پاسخ به الگوی مشخص بین پیکسل‌های محلی با قدرت فراوانی فعال‌سازی می‌شود.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

با نگاهی سطحی به فرمول کانولوشن ممکن است نتوان به این حقیقت پی برد که تمام این خواص مختلف ریشه در ریاضیات کانولوشن دارد. در واقع، با درک بهتر مفهوم کانولوشن، می‌توان به نحوه عملکرد متفاوت آن در کاربردهای مختلف پی برد.

برای شروع کار بهتر است بار دیگر فرمول کانولوشن را یاد آوری کنیم:

$$(f * g)(t) \stackrel{\text { def }}{=} \int_{-\infty}^{\infty} f(\tau) g(t-\tau) d \tau$$

این فرمول برای کسانی که با فیلترهای کانولوشنی کار می‌کنند، ممکن است نامانوس به نظر برسد. در فرمول بالا، توابع f و g هر دو روی دامنه ورودی یکسانی عمل می‌کنند. این فرمول از دیدگاه آماری بیان‌کننده تابع چگالی است. همچنین در پردازش سیگنال، فرمول بالا یک شکل موج را بیان کند. اما در اینجا می‌توان رابطه را فقط به عنوان یک تابع عمومی در نظر گرفت. هنگامی که دو سیگنال در یکدیگر کانولوشن می‌شوند، عملگر کانولوشن خود مانند یک تابع عمل می‌کند، بنابراین می‌توان مقدار کانولوشن را در هر نقطه معین t، دقیقا مانند یک تابع به دست آورد.

در واقع، برای محاسبه کانولوشن بین دو تابع f و g در نقطه t باید از تمام مقادیر متغیر $$\tau$$ از منفی بی‌نهایت تا مثبت بی‌نهایت انتگرال بگیریم و در هر نقطه، مقدار تابع $$f(x)$$ در $$\tau$$ را در تابع $$g(x)$$ در نقطه $$t-\tau$$ ضرب کنیم. بنابراین بیان ریاضی کانولوشن دو سیگنال ساده به نظر می‌رسد. اما هنوز واضح نیست که این عملگر چگونه می تواند این همه کاربردهای متنوع داشته باشد. برای بیان این موضوع، بهتر است به چند مثال بپردازیم.

کاربرد کانولوشن به عنوان تابع صاف کننده (Smoothing)

یک راه برای درک بهتر کانولوشن، این است که آن را به تخمین چگالی کرنل (Kernel Density Estimation) یا به اختصار KDE تشبیه کنیم. در KDE، از یک کرنل مانند کرنل گاوسی (Gaussian) استفاده می‌شود و برای تخمین چگالی یک دیتاست، کپی‌هایی از کرنل به مرکز تمام نقاط در دیتاست با هم جمع می‌شوند. در هر جایی که تجمع نقاط دیتاست بیشتر باشد، تعداد بیشتری از توابع کرنل با هم جمع می‌شوند و این فرایند به تدریج باعث محاسبه تقریبی از تابع چگالی احتمالاتی می‌شود. مهم‌ترین نکته‌ای که در مقایسه این دو مفهوم باید مورد توجه قرار گیرد این است که چگونه کرنل در اطراف نقاط مختلف دیتاست مانند یک صاف‌کننده عمل می‌کند.

اگر از یک هیستوگرام ساده استفاده کنیم و یک واحد جرم را به سادگی در محل هر داده قرار دهیم، آن‌گاه نتیجه خروجی مخصوصا در نمونه‌های با سایز کوچک بسیار پرشکاف و گسسته خواهد بود. اما با استفاده از یک کرنل که جرم را در حوالی یک نقطه پخش می‌کند، می‌توان توابع‌صاف‌تر و نرم‌تر را در خروجی به دست آورد. دلیل تمایل ما به استفاده از توابع با تغییرات نرم این است که اکثر پدیده‌های موجود در طبیعت نیز دارای تغییرات نرم هستند.

تمایز مهمی که وجود دارد این است که در کانولوشن، به جای صاف کردن تابع با استفاده از توزیع تجربی نقاط داده، از یک روش عمومی‌تر استفاده می‌کنیم که ما را قادر می‌سازد هر تابع $$f(x)$$ را صاف کنیم. البته در حالت کلی، این روش نیز تشابه زیادی با روش تخمین چگالی دارد. در واقع، این بار به جای تابع گاوسی، از تابع $$g(x)$$ به عنوان تابع کرنل استفاده می‌کنیم و در هر نقطه از انتگرال، یک کپی از $$g(x)$$ را در مقدار $$f(x)$$ در همان نقطه ضرب می‌کنیم. در تصویر زیر نمایی از این فرایند نشان داده شده است.

در این تصویر، تابع اولیه $$f(x)$$ نشان داده شده است. در واقع، این همان تابع دارای نویز است که می‌خواهیم آن را صاف‌تر کنیم.

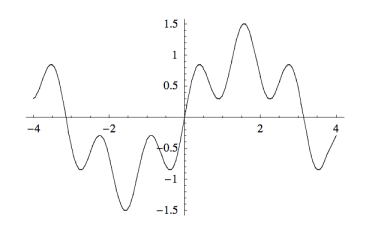
نمودار پایین سمت چپ، تابع کرنل فرایند را نشان می‌دهد که در اینجا تابع گاوسی $$g(x)$$ انتخاب شده است. مرکز تابع گوسی در هر نقطه قرار می‌گیرد و در مقدار تابع $$f(x)$$ در همان نقطه ضرب (مقیاس) می‌شود. در نمودار پایین سمت راست، نتیجه نهایی حاصل از کانولوشن ($$f(x) * g(x)$$) نشان داده شده است که در واقع حاصل جمع تمام توابع کرنل مقیاس شده است.

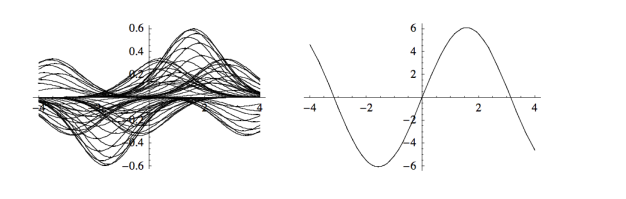
کاربرد کانولوشن به عنوان گردآورنده داده‌های محلی

در این قسمت تا حدودی با کاربرد کانولوشن در شبکه‌های عصبی آشنا می‌شویم. در این کاربرد، کانولوشن به عنوان نوعی گردآورنده اطلاعات (Information Aggregation) مورد استفاده قرار می‌گیرد، اما این گردآوری از منظر یک نقطه خاص انجام می‌پذیرد. این نقطه همانی است که کانولوشن در آن محاسبه می‌شود. می‌توان این نقطه را نقطه خروجی نامید و نقطه‌ای که در آن انتگرال محاسبه می‌شود را نقطه ورودی نامید. هدف نقطه خروجی این است که اطلاعات راجع به مقدار $$f(x)$$ را در طول دامنه تابع خلاصه کند و این کار را بر اساس قانون خاصی انجام می‌دهد.

می‌توان گفت قانون به این صورت است که نقطه خروجی فقط به مقادیری از تابع f اهمیت می‌دهد که یک واحد از آن فاصله دارند و به اطلاعات نقاط فراتر از آن احتیاجی ندارد. قانون دیگر می‌تواند این باشد که نقطه خروجی بیشتر به نقاطی از فضا اهمیت می‌دهد که نزدیک‌تر به خودش باشند و به جای اینکه از یک فاصله آستانه به بعد تاثیر را ناگهانی به صفر برساند، به صورت تدریجی با افزایش فاصله تاثیر را کاهش می‌دهد. حتی نقطه خروجی می‌تواند به نقاط دوردست اهمیت بیشتری بدهد. تمام این گردآوری‌های مختلف، می‌توانند در قالب مفهوم کانولوشن بگنجند و با تابع $$g(x)$$ بیان شوند.

از دیدگاه ریاضی می‌توان کانولوشن را به عنوان مجموع وزن‌دار مقادیر $$f(x)$$ در نظر گرفت. این کار به طریقی انجام می‌گیرد که مشارکت هر x با توجه به میزان فاصله بین آن نقطه و نقطه خروجی t تعیین می‌شود. به بیان دقیق‌تر می‌توان گفت که برای تعیین وزن‌ها، این سوال مطرح می‌شود که اگر یک کپی از تابع $$g(x)$$ به مرکز هر نقطه x قرار داده شود، آن‌گاه مقدار تابع کپی شده در نقطه خروجی t چقدر خواهد بود؟

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

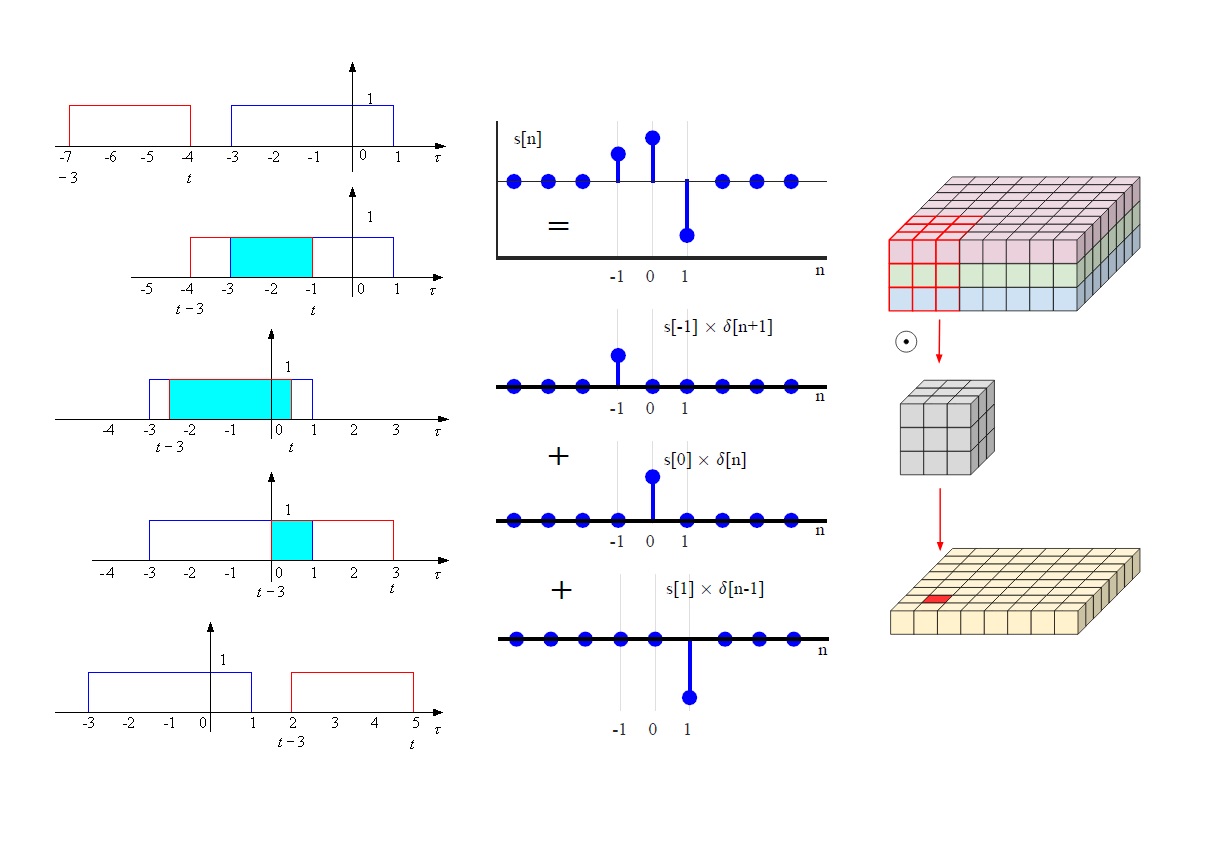
برای تجسم این موضوع تصویر زیر را در نظر بگیرید. در این مثال، از تابع $$g(x) = x^ 2$$ استفاده شده است. حال توجه کند که مقدار وزن‌ها در مجموع وزن‌دار چگونه در $$x= -2$$ محاسبه شده‌اند.

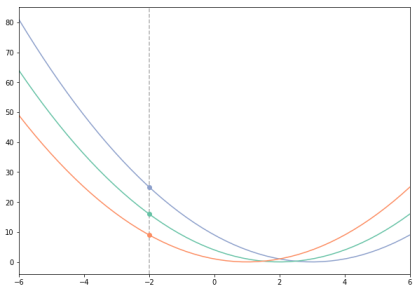
در تصویر بالا، نمودار نارنجی رنگ، همان تابع $$g(x)$$ است که مرکز آن در نقطه $$x = 1$$ قرار داده شده است و مقدار آن در $$x = -2$$ برابر با 9 به دست می‌آید. نمودارهای سبز و آبی رنگ، نشان‌دهنده تابع $$g(x)$$ هستند که مرکز آن به ترتیب به نقاط $$x = 2$$ و $$x = 3$$ منتقل شده است و مقدار آن‌ها در $$x = -2$$ برابر با 16 و 25 به دست می‌آید. اگر f را به صورت تابعی در نظر بگیریم که فقط مقادیر غیرصفر در ۱ و ۲ و 3 می‌پذیرد، آن‌گاه می‌توان مقدار $$(f*g)(-2)$$ را به صورت $$9* f(1) + 16 * f(2) + 25* f(3)$$ محاسبه کرد. توجه کنید که در این مثال، نقطه $$x = -2$$ برابر با نقطه خروجی و نقاط 1 و 2 و 3 برابر با نقاط ورودی هستند.

با دقت در تصویر بالا، می‌توان به ارتباط بین کاربرد کانولوشن به عنوان گردآورنده و KDE که در قسمت قبل بیان شد، پی برد. زمانی که دقت خود را روی یک نقطه ورودی خاص متمرکز می‌کنیم، هر نقطه از کپی‌های تابع $$g(x)$$ به این پرسش پاسخ می‌دهد که اطلاعات $$f(x)$$ چگونه در اطراف آن نقطه پراکنده شده‌اند؟

اما زمانی که روی یک نقطه خروجی خاص تمرکز می‌کنیم، در واقع این سوال را مطرح می‌کنیم که مشارکت و سهم سایر نقاط در گردآوری داده‌های $$f(x)$$ در آن نقطه خروجی چه میزان قوی است؟

هر خط عمودی که مانند تصویر بالا بر روی کپی‌های شیفت یافته تابع $$g(x)$$ ترسیم شود، متناظر با مقدار کانولوشن در یک نقطه خاص x است و محل تقاطع آن خط با توابع انتقالی $$g(x)$$ وزن تابع $$f(x)$$ در نقطه x را نشان می‌دهد که مرکز تابع در آن نقطه قرار گرفته است.

کانولوشن در شبکه عصبی

عملکرد کانولوشن در گردآوری داده‌ها ما را یک گام دیگر به کاربرد آن در شبکه‌های عصبی نزدیک‌تر می‌کند. در یک شبکه عصبی، کانولوشن قادر است که رفتار لایه در ناحیه محلی اطراف یک نقطه را خلاصه کند. البته دو مشکل هنوز در بیان این کاربرد وجود دارد.

مشکل اول این است که در نگاه اول، فیلتر کانولوشن یک تصویر با آن‌چه که تا اینجا بیان کردیم بسیار متفاوت به نظر می‌رسد. زیرا فیلترها ۲ بعدی و گسسته هستند، در حالیکه در مثال‌هایی که تا این قسمت بررسی کردیم، تک بعدی و پیوسته بودند. این مشکل در واقع بسیار ساده است. اگر در تمام مثال‌های بالا، توابع f و g را در فضای دو بعدی $$(x_1, x_2)$$ تعریف کنیم و سپس هر کدام را به بازه‌های گسسته بشکنیم که در هر بازه مقدار توابع ثابت باشد، آن‌گاه به سادگی این تفاوت حل می‌شود.

نکته‌ مهمی که درباره تفاوت بین کانولوشن در کاربرد متداول و کانولوشن در شبکه عصبی وجود دارد این است که زمانیکه گردآوری محلی در شبکه عصبی اتفاق می‌افتد، می‌توان آن را به صورت یک کرنل وزن‌‌دهنده متمرکز در نقطه گردآوری بیان کرد که اطلاعات را از اطراف بر اساس تابع کرنل جمع‌آوری می‌کند. یک فیلتر کانولوشن در شبکه عصبی از وزن تمام نقاط ورودی اطراف نقطه خروجی و نیز وزن خود نقطه خروجی تشکیل شده است. نمایی از نحوه عملکرد کانولوشن در شبکه عصبی در تصویر زیر دیده می‌شود.

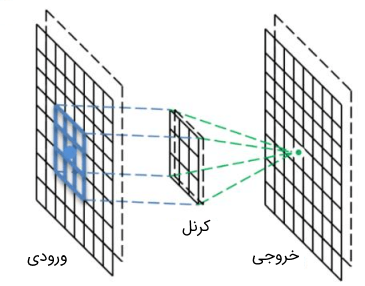
البته به این نکته باید توجه کرد که در کانولوشن تعریف ریاضی، کرنل وزن $$g(x)$$ خود را در اطراف نقطه خروجی متمرکز نمی‌کند. در فرمول کانولوشن، کپی‌هایی از $$g(x)$$ در هر نقطه ورودی متمرکز شده‌اند و مقدار تابع کپی‌شده در یک خروجی معین، تعیین کننده وزن نقطه ورودی در آن نقطه است. بنابراین فیلترهای کرنل در شبکه عصبی مشابه با $$g(x)$$ در فرمول کانولوشن نیستند. اگر بخواهیم از یک فیلتر شبکه استفاده کنیم و آن را با استفاده از فرمول کانولوشن اعمال کنیم، باید فیلتر را در حالت یک بعدی بلغزانیم و یا در حالت دو بعدی به صورت قطری حرکت دهیم. در حالت معکوس، اگر بخواهیم یک تابع $$g(x)$$ را از انتگرال کانولوشن اتخاذ کنیم و از آن به عنوان فیلتر متمرکز در خروجی استفاده کنیم، آن‌گاه فیلتر برابر با $$g(-x)$$ خواهد بود.

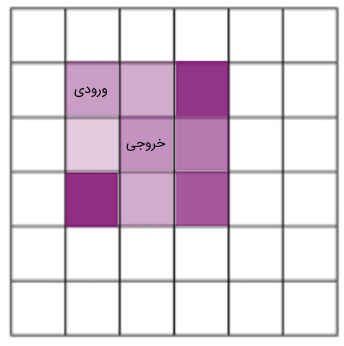
در حالتی که کرنل متقارن باشد، این موضوع اهمیتی ندارد. اما در فیلترهای کانولوشن معمولی تقارن وجود ندارد و وزن‌های موقعیت مورب، با یکدیگر تفاوت دارند. بنابراین اگر یک فیلتر متمرکز در خروجی را در نظر بگیرید و بخواهید از آن در یک قالب کانولوشن مناسب متمرکز در نقطه ورودی استفاده کنید، وزن‌های مختلفی را به دست می‌آورید. این مفهوم در تصاویر زیر به صورت واضحی نشان داده شده است.

$$g(x)$$" width="344" height="346">

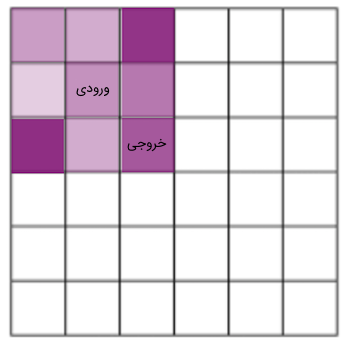$$g(x)$$" width="344" height="346">

در تصویر اول، از یک نسخه متمرکز در خروجی و در تصویر دوم، از یک نسخه متمرکز در ورودی کرنل $$g(x)$$ برای تولید وزن‌‌های هر ورودی استفاده شده است. در این حالت مشاهده می‌شود که نمی‌توان از یک کرنل یکسان در هر دو حالت استفاده کرد و نتایج یکسانی به دست آورد. این واقعیت که نمی‌توان به صورت مستقیم کرنل متمرکز در خروجی را مانند $$g(x)$$ در کانولوشن مورد استفاده قرار داد، یک تفاوت مهم است.

کانولوشن به عنوان تطبیق الگو

تا اینجا دانستیم که چگونه فیلترهای وزن متحرک می‌توانند با یک رابطه ریاضی انتگرالی در ارتباط باشند. در این قسمت می‌خواهیم بدانیم چگونه فیلترهای وزن به عنوان تطبیق الگو عمل می‌کنند. فیلترهای کانولوشنی معمولا بر اساس عملگر تطبیق الگو توصیف می‌شوند. اما چرا در این حالت هر قدر مقدار $$f(x)$$ در حوالی یک نقطه مشابه با وزن‌های فیلتر بیشتر باشد، مقدار کانولوشن در آن نقطه بیشتر خواهد بود؟ لازم به ذکر است که در این حالت نیز $$f(x)$$ مقادیر پیکسل‌ها و یا مقادیر لایه‌های پایین‌تر شبکه هستند.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

یک پاسخ ساده به پرسش بالا این است که کانولوشن گسسته معادل با یک ضرب نقطه‌ای بین وزن‌های فیلتر و مقادیر زیر فیلتر است و از نظر هندسی، عملگر ضرب نقطه‌ای مقیاسی برای سنجیدن شباهت برداری است. کانولوشن متمرکز در خروجی، برداری از وزن‌ها و برداری از مقادیر ورودی را دریافت می‌‌کند و مقادیر هم‌تراز را در یکدیگر ضرب و سپس با هم جمع می‌کند. این دقیقا همان روندی است که عملگر ضرب نقطه‌ای نیز انجام می‌دهد. واضح است که با افزایش دامنه یک یا هر دو بردار در ضرب نقطه‌ای می‌توان مقدار ضرب را افزایش داد. اما زمانی که دامنه‌ها ثابت باشند، بیشینه مقدار ضرب در زمانی حاصل می‌شود که بردارها در یک جهت یکسان باشند. در شبکه عصبی بیشینه حاصل‌ضرب زمانی به دست می‌آید که الگوی شدت (Intensity) در مقادیر پیکسل‌ها با وزن‌های بالا و پایین در فیلتر وزن منطبق باشد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌های داده کاوی و یادگیری ماشین
• آموزش یادگیری عمیق (Deep learning)
• انرژی و توان سیگنال — از صفر تا صد
• نمونه برداری سیگنال — راهنمای جامع
• یادگیری عمیق (Deep Learning) با پایتون — به زبان ساده

^^