رابطه پارسوال در سری فوریه – از صفر تا صد (+ دانلود فیلم آموزش رایگان)
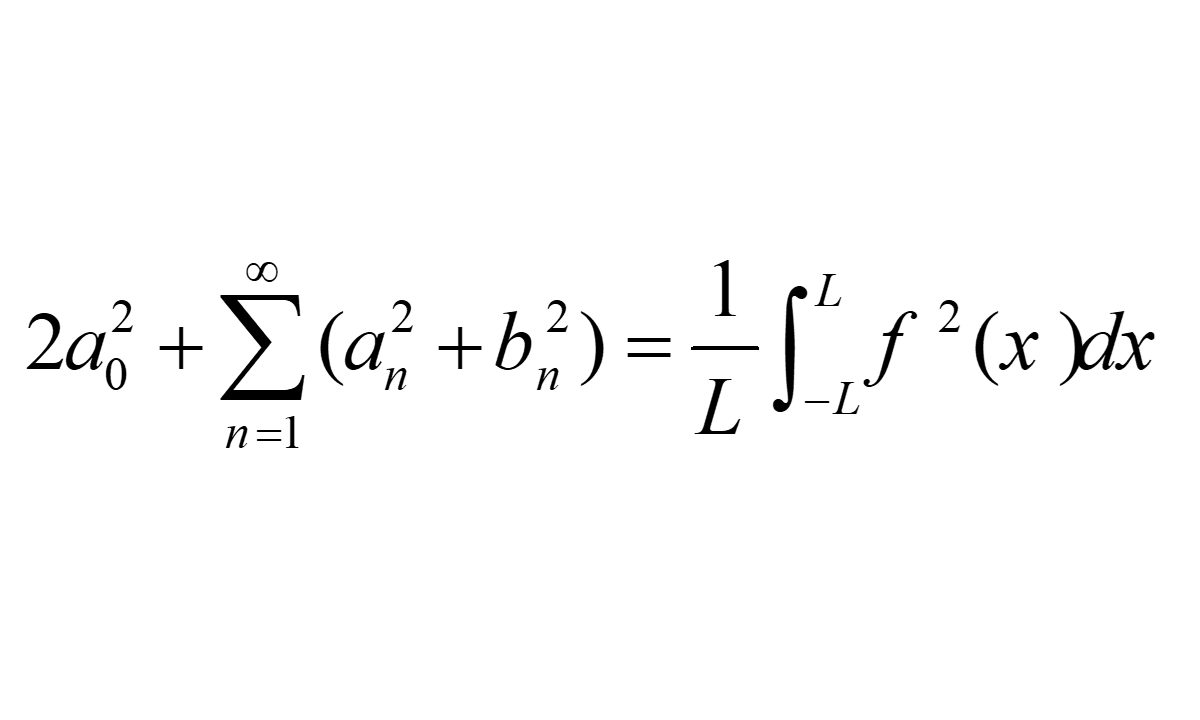
رابطه پارسوال یک رابطه بسیار پرکاربرد در سری فوریه توابع متناوب است. یکی از کاربردهای ویژه رابطه پارسوال محاسبه سریها است. در این مقاله، ابتدا سری فوریه به صورت خلاصه بیان میشود. سپس نامساوی بسل و حالت ویژه آن که همان رابطه پارسوال است مورد بررسی قرار میگیرد و در نهایت با حل چندین مثال نحوه محاسبه سریها توسط رابطه پارسوال بیان میشود.
سری فوریه
سری فوریه توابع مثلثاتی بصورت زیر بیان میشود:
$${f\left( x \right) = \frac{{{a_0}}}{2} \text{ + }}\kern0pt{ \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos \frac{{n\pi x}}{L} + {b_n}\sin\frac{{n\pi x}}{L}} \right)}}$$
با فرض دوره تناوب 2L، ضرایب سری فوریه توسط روابط زیر بدست میآیند:
$${{{a_0} }={ \frac{1}{L}\int\limits_{ – L}^L {f\left( x \right)dx} ,\;\;}}\kern-0.3pt {{{a_n} }={ \frac{1}{L}\int\limits_{ – L}^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} ,\;\;}}\kern-0.3pt {{{b_n} }={ \frac{1}{L}\int\limits_{ – L}^L {f\left( x \right)\sin\frac{{n\pi x}}{L}dx} .}}$$
یکی از حالتهای پرکاربرد سری فوریه زمانی است که دوره تناوب آن برابر $$2\pi$$ باشد. در این شرایط سری فوریه ساده شده، به صورت زیر بیان خواهد شد:
$${f\left( x \right) = \frac{{{a_0}}}{2} }+{ \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos nx + {b_n}\sin nx} \right)} .}$$
و ضرایب آن توسط معادلات زیر قابل محاسبه است:
$${{a_0} = \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)dx} ,\;\;\;}\kern-0.3pt {{a_n} = \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)\cos nx dx} ,\;\;\;}\kern-0.3pt {{b_n} = \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)\sin nx dx} .}$$
در مورد روابط سری فوریه دقت کنید که ضرایب $${{a_n}}$$ و $${{a_0}}$$ بخش زوج تابع را تشکیل میدهند. بنابراین اگر تابع متناوب زوج باشد، فقط این ضرایب وجود خواهند داشت و ضریب $${{b_n}}$$ صفر میشود. به صورت مشابه، $${{b_n}}$$ بخش فرد تابع را مشخص میکند و اگر خود تابع فرد باشد، فقط این ضریب مخالف صفر خواهد بود.
حل یک مثال از سری فوریه
فرض کنید که تابع زیر در بازه $$\left[ { – \pi ,\pi }\right]$$ متناوب باشد:
$${f\left( x \right) \text{ = }}\kern0pt
{\begin{cases}
0, & \text{if} & – \pi \le x \le 0 \\
1, & \text{if} & 0 < x \le \pi
\end{cases}.}$$
در این صورت ضرایب سری فوریه آن به صورت زیر محاسبه میشوند:
$${{a_0} = \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\int\limits_0^\pi {1dx} } = {\frac{1}{\pi } \cdot \pi }={ 1.}$$
$${{a_n} = \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {1 \cdot \cos nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_0^\pi } \right] } = {\frac{1}{{\pi n}} \cdot 0 }={ 0,}$$
دقت کنید که $$\cos n\pi = {\left( { – 1} \right)^n}$$ است. بنابراین با استفاده از این تساوی، رابطه بالا به صورت زیر ساده خواهد شد:
$${b_n} = \frac{{1 – {{\left( { – 1} \right)}^n}}}{{\pi n}}.$$
و در نهایت سری فوریه به شکل زیر بیان میشود:
$${f\left( x \right) = \frac{1}{2} }+{ \sum\limits_{n = 1}^\infty {\frac{{1 – {{\left( { – 1} \right)}^n}}}{{\pi n}}\sin nx} .}$$
شکل باز شده سری فوریه نیز به فرم زیر خواهد بود:
$${f\left( x \right) = \frac{1}{2} }+{ \frac{{1 – \left( { – 1} \right)}}{\pi }\sin x }
+ {\frac{{1 – {{\left( { – 1} \right)}^2}}}{{2\pi }}\sin 2x }
+ {\frac{{1 – {{\left( { – 1} \right)}^3}}}{{3\pi }}\sin 3x }
+ {\frac{{1 – {{\left( { – 1} \right)}^4}}}{{4\pi }}\sin 4x }
+ {\frac{{1 – {{\left( { – 1} \right)}^5}}}{{5\pi }}\sin 5x + \ldots }
\\= {\frac{1}{2} + \frac{2}{\pi }\sin x }
+ {\frac{2}{{3\pi }}\sin 3x }
+ {\frac{2}{{5\pi }}\sin 5x + \ldots }$$
لازم به ذکر است که در این مثال، تابع فرد نیست ولی $${{ a_n = 0}}$$ و $${{a_0 = 1}}$$ شده است. در واقع اگر نیم واحد را از تابع کم کنیم، یک تابع متناوب و فرد به دست میآید که در این صورت، با توجه به ویژگیهایی که بیان کردیم، $${{ a_n = 0}}$$ میشود. نیم واحدی کسر شده، در مقدار ثابت سری فوریه یعنی $${{a_0}}$$ قرار میگیرد. چنین توابعی را توابع شبه فرد میگویند.
نامساوی بسل
در مطالب قبلی مجله فرادرس به معادله دیفرانسیل بسل پرداخته شد. اما نامساوی بسل (Bessel’s Inequality) یک قید منطقی را بین تابع و ضرایب سری فوریه آن برقرار میکند. طبق این رابطه برای هر عدد صحیح $$N>0$$ رابطه زیر برقرار است:
$${\frac{{{a_0^2}}}{2} + \sum\limits_{n = 1}^N {\left( {a_n^2 + b_n^2} \right)} }\le{ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {{f^2}\left( x \right)dx} .}$$
اما مفهوم این رابطه چیست؟ واضح است که طرف راست نامساوی، بیانگر میانگین انرژی تابع در یک دوره تناوب آن است. از طرف دیگر میدانیم که میانگین انرژی برای یک تابع سینوس و یا کسینوس، در یک دوره تناوب، برابر است با توان دوم دامنه تابع تقسیم بر 2. پس با این توضیحات میتوان گفت سمت چپ نامساوی بسل بیانگر مجموع انرژیهای N جمله اول سری فوریه است.
حال با توجه به اینکه در سری فوریه بینهایت جمله وجود دارد و ما فقط N جمله اول آن را در نظر گرفتهایم، بدیهی است که مجموع انرژی این تعداد محدود از جملات سری فوریه، کمتر از انرژی کل تابع باشد. دقت کنید در صورتی که دو تابع با هم برابر باشند، انرژی آنها نیز یکسان است.
نامساوی بسل بخصوص در اثبات همگرایی سریها کاربرد ویژهای دارد؛ زیرا سری فوریه برای توابعی تعریف میشود که انرژی محدود دارند. طبق نامساوی بسل، سری $$\sum\limits_{n = 1}^N {\left( {a_n^2 + b_n^2} \right)}$$ برای هر $$N>0$$ همگرا خواهد شد.
یکی دیگر از کاربردهای نامساوی بسل، محاسبه خطای تقریب توابع است. فرض کنید برای تقریب یک تابع به صورت مجموع محدودی از سینوسیها و کسینوسیها از ضرایب سری فوریه استفاده شود. آنگاه خطای تقریب بصورت زیر محاسبه میشود:
$$E^{*}=\int_{-L}^{L} f(x)^{2}dx-\pi(\frac {a_{0}^{2}}{2}+\sum_{n=1}^\infty (a_{n}^{2}+b_{n}^{2}))$$
هر چقدر تعداد جملات بیشتری درنظر گرفته شود، خطای تقریب نیز کمتر خواهد شد. برای مثال فرض کنید تابع $$f(x)=x+\pi$$ در بازه $$[-\pi,\pi]$$ متناوب باشد. نمودار این تابع در شکل زیر رسم شده است.
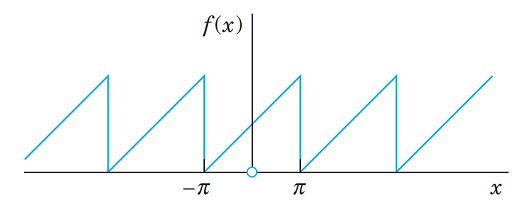
در این شرایط جدول زیر خطای تقریب تابع به ازای تعداد جملات مختلف را نشان می دهد.

طبق جدول بالا اگر فقط جمله اول سری فوریه در نظر گرفته شود، خطای تقریب 8.1045 است. اگر دو جمله لحاظ شود، خطا به 4.9629 کاهش پیدا میکند. اگر 20 جمله اول سری فوریه به عنوان تقریب تابع موج دندان ارهای فرض شود، آنگاه خطای تقریب برابر با 0.6129 میشود. در نهایت با فرض 1000 جمله اول خطای خیلی کوچک و مساوی با 0.0126 خواهد شد. شکل زیر نمودار تابع تقریبی به ازای 20 جمله اول را نشان میدهد. واضح است که این نمودار به نمودار تابع اصلی خیلی نزدیک شده است.

رابطه پارسوال
رابطه پارسوال (Parseval) مشابه نامساوی بسل است با این تفاوت که $$N = \infty$$ است یا به عبارت دیگر، تمام بینهایت جمله سری فوریه در نظر گرفته میشود. بنابراین در این شرایط نامساوی به مساوی تبدیل خواهد شد و رابطه پارسوال به فرم زیر ارائه میشود:
$${\frac{{{a_0^2}}}{2} + \sum\limits_{n = 1}^\infty {\left( {a_n^2 + b_n^2} \right)} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {{f^2}\left( x \right)dx} .}$$
این رابطه برای توابع با دوره تناوب $$2\pi$$ نوشته شده است و برای توابع با دوره تناوب دلخواه $$2L$$ کافی است که در رابطه بالا به جای $$\pi$$ از $$L$$ استفاده شود.
باید دقت کرد که رابطه بسل و پارسوال فقط برای توابعی برقرار هستند که انرژی محدود دارند و یا به عبارت دیگر توان دوم آنها انتگرالپذیر باشد.
رابطه پارسوال برای سری فوریه مختلط
سری فوریه مختلط و نمایی، یک شکل بسته دیگر برای سری فوریه توابع متناوب است که به صورت زیر بیان میشود:
$$f\left( x \right) = \sum\limits_{n = – \infty }^\infty {{c_n}{e^{inx}}} ,$$
که در آن ضرایب سری فوریه مختلط توسط رابطه زیر قابل محاسبه هستند:
$${{c_n} }={ \frac{1}{{2\pi }}\int\limits_{ – \pi }^\pi {f\left( x \right){e^{ – inx}}dx} .}$$
در این شرایط رابطه پارسوال باید بر حسب ضرایب جدید بازنویسی شود و رابطه جدید برابر است با:
$${\sum\limits_{n = – \infty }^\infty {{{\left| {{c_n}} \right|}^2}} }={ \frac{1}{{2\pi }}\int\limits_{ – \pi }^\pi {{f^2}\left( x \right)dx} .}$$
این رابطه از این حقیقت نشات گرفته است که انرژی تابع مختلط $$c_{n}e^{i\omega t}$$ برابر است با $${|c_{n}|^{2}}$$. بنابراین برای برقراری رابطه سری فوریه مختلط، انرژی آنها باید یکسان باشد.
اگر انرژی طرفین رابطه سری فوریه مختلط را محاسبه کنیم، دقیقا به رابطه پارسوال در شکل مختلط میرسیم. البته با استفاده از روابط زیر که ارتباط بین ضرایب سری فوریه حقیقی و مختلط را نشان میدهند، میتوان به رابطه پارسوال در شکل مختلط رسید:
$$a_{n}=c_{n}+c_{-n}$$
$$b_{n}=i(c_{n}-c_{-n})$$
$$a_{0}=2c_{0}$$
یکی از کاربردهای ویژه رابطه پارسوال محاسبه سریها است که در ادامه با چندین مثال نشان داده خواهد شد.
مثال ۱
حاصل سری $$\sum\limits_{n = 1}^\infty {\large\frac{1}{{{n^2}}\normalsize}}$$ را به دست آورید.
حل
برای محاسبه سری، تابع $$f\left( x \right) = x$$ در بازه $$\left[ { – \pi ,\pi } \right]$$ در نظر گرفته میشود. فرض میکنیم تابع دارای دوره تناوب $$2\pi$$ باشد. به دلیل اینکه تابع فرد است، ضرایب $${a_0} = {a_n} = 0$$ میشود و فقط ضرایب سینوسیها وجود خواهد داشت. طبق روابطی که بیان شد، ضریب $${b_n}$$ به فرم زیر محاسبه میشود:
$${{b_n} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\int\limits_{ – \pi }^\pi {x\sin nxdx} .}$$
برای محاسبه این انتگرال از قضیه انتگرالگیری جز به جز ($${\int\limits_{ – \pi }^\pi {udv} = \left. {\left( {uv} \right)} \right|_{ – \pi }^\pi }-{ \int\limits_{ – \pi }^\pi {vdu}}$$) استفاده میکنیم. با استفاده از این قضیه انتگرال بالا به صورت زیر محاسبه میشود:
$${{b_n} = \frac{1}{\pi }\int\limits_{ – \pi }^\pi {x\sin nxdx} }
= {{\frac{1}{\pi }\Big[ {\left. {\left( { – \frac{{\cos nx}}{n}} \right)} \right|_{ – \pi }^\pi }}}-{{{ \int\limits_{ – \pi }^\pi {\left( { – \frac{{\cos nx}}{n}} \right)dx} } \Big] }}
\\= {{\frac{1}{{n\pi }}\Big[ { – 2\pi \cos n\pi }}+{{ \left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_{ – \pi }^\pi } \Big] }}
= {{\frac{1}{{n\pi }}\Big[ { – 2\pi \cos n\pi }}}+{{{ \frac{1}{n}\left( {\sin n\pi – \sin \left( { – n\pi } \right)} \right)} \Big] }}
\\= {\frac{1}{{n\pi }}\left[ { – 2\pi \cos n\pi + \frac{{2\sin n\pi }}{n}} \right] }
= {\frac{2}{{n\pi }}\left[ {\frac{{\sin n\pi }}{n} – \pi \cos n\pi } \right].}$$
عبارت نهایی با استفاده از روابط $$\sin n\pi = 0$$ و $$\cos n\pi = {\left( { – 1} \right)^n}$$ به فرم زیر ساده میشود:
$${{b_n} = \frac{2}{{n\pi }}\left( { – \pi {{\left( { – 1} \right)}^n}} \right) } = { – \frac{2}{n}{\left( { – 1} \right)^n} } = {\frac{2}{n}{\left( { – 1} \right)^{n + 1}}.}$$
در نهایت نمایش سری فوریه تابع متناوب $$f\left( x \right) = x$$ در بازه $$\left[ { – \pi ,\pi } \right]$$ به شکل زیر خواهد بود:
$$x = \sum\limits_{n = 1}^\infty {\frac{2}{n}{{\left( { – 1} \right)}^{n + 1}}\sin nx} .$$
حال ضرایب به دست آمده را در رابطه پارسوال قرار میدهیم:
$${{\sum\limits_{n = 1}^\infty {{{\left[ {\frac{2}{n}{{\left( { – 1} \right)}^{n + 1}}} \right]}^2}} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {{x^2}dx} ,\;\;}}\\{{4\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} }={ \frac{1}{\pi }\left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_{ – \pi }^\pi } \right],\;\;}}\\{{\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} }={ \frac{1}{{4\pi }}\left( {\frac{{{\pi ^3}}}{3} – \frac{{{{\left( { – \pi } \right)}^3}}}{3}} \right),\;\;}}\Rightarrow{{\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} }={ \frac{1}{{4\pi }} \cdot \frac{{2{\pi ^3}}}{3} }={\frac{{{\pi ^2}}}{6}.}}$$
بنابراین حاصل سری مذکور برابر با $$\frac{\pi^{2}}{6}$$ خواهد شد.
مثال ۲
رابطه پارسوال را به تابع متناوب $$f\left( x \right) = {x^2}$$ در بازه $$\left[ { – \pi ,\pi } \right]$$ اعمال کنید.
حل
این تابع متناوب و زوج است، پس ضرایب سینوسیها حذف خواهد شد. سایر ضرایب به فرم زیر تعیین میشوند:
$${{a_0} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\int\limits_{ – \pi }^\pi {{x^2}dx} = \frac{2}{\pi }\int\limits_0^\pi {{x^2}dx} } = {\frac{2}{\pi } \cdot \left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^\pi } \right] } = {\frac{2}{\pi } \cdot \frac{{{\pi ^3}}}{3} } = {\frac{{2{\pi ^2}}}{3},}$$
$${{a_n} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {{x^2}\cos nxdx}} \\ = {\frac{4}{{\pi {n^2}}}\left[ {\pi \cos n\pi – \frac{{\sin n\pi }}{n}} \right]}$$
بنابراین نمایش سری فوریه تابع بصورت زیر خواهد بود:
$${f\left( x \right) = {x^2} }={ \frac{{{\pi ^2}}}{3} }+{ \sum\limits_{n = 1}^\infty {\frac{4}{{{n^2}}}{{\left( { – 1} \right)}^n}\cos nx} ,}$$
حال ضرایب و تابع متناوب را در رابطه پارسوال قرار میدهیم:
$${\frac{{{a_0^2}}}{2} + \sum\limits_{n = 1}^\infty {\left( {a_n^2 + b_n^2} \right)} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {{f^2}\left( x \right)dx} ,\;\;}\\
{\frac{1}{2}{\left( {\frac{{2{\pi ^2}}}{3}} \right)^2} }+{ \sum\limits_{n = 1}^\infty {{{\left[ {\frac{4}{{{n^2}}}{{\left( { – 1} \right)}^n}} \right]}^2}} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {{x^4}dx} ,\;\;}\\
{\frac{{2{\pi ^4}}}{9} + 16\sum\limits_{n = 1}^\infty {\frac{1}{{{n^4}}}} }={ \frac{1}{\pi }\left[ {\left. {\left( {\frac{{{x^5}}}{5}} \right)} \right|_{ – \pi }^\pi } \right],\;\;}\\
{\frac{{2{\pi ^4}}}{9} + 16\sum\limits_{n = 1}^\infty {\frac{1}{{{n^4}}}} }={ \frac{1}{\pi } \cdot \frac{{2{\pi ^5}}}{5},\;\;}\\
{16\sum\limits_{n = 1}^\infty {\frac{1}{{{n^4}}}} }={ \frac{{2{\pi ^4}}}{5} – \frac{{2{\pi ^4}}}{9},\;\;}\\
{16\sum\limits_{n = 1}^\infty {\frac{1}{{{n^4}}}} = \frac{{8{\pi ^4}}}{{45}},\;\;}\\
{\sum\limits_{n = 1}^\infty {\frac{1}{{{n^4}}}} = \frac{{{\pi ^4}}}{{90}}.}$$
بنابراین حاصل سری $$\sum\limits_{n = 1}^\infty {\frac{1}{{{n^4}}}}$$ برابر با $$\frac{{{\pi ^4}}}{{90}}$$ میشود.
مثال ۳
با اعمال رابطه پارسوال به تابع متناوب زیر حاصل سریهای $$\sum\limits_{n = 1}^\infty {\large\frac{{{{\sin }^2}nd}}{{{n^2}}}\normalsize}$$ و $$\sum\limits_{n = 1}^\infty {\large\frac{{{{\cos }^2}nd}}{{{n^2}}}\normalsize}$$ را به دست آورید.
$${f\left( x \right) \text{ = }}\kern0pt
{\begin{cases}
1, & \text{if} & 0 \le \left| x \right| \le d \\
0, & \text{if} & d \le \left| x \right| \le \pi
\end{cases},}$$
حل
نمایش سری فوریه تابع داده شده بصورت زیر به دست میآید:
$${f\left( x \right) = \frac{d}{\pi } }+{ \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{\sin nd}}{n}\cos nx} .}$$
در نتیجه ضرایب سری فوریه برابر هستند با:
$${{a_0} = \frac{{2d}}{\pi },\;\;}\kern0pt{{a_n} = \frac{{2\sin nd}}{{n\pi }},\;\;}\kern0pt{{b_n} = 0.}$$
حال ضرایب سری فوریه و تابع آن را در رابطه پارسوال قرار میدهیم:
$${\frac{{{a_0^2}}}{2} + \sum\limits_{n = 1}^\infty {\left( {a_n^2 + b_n^2} \right)} }={ \frac{1}{\pi }\int\limits_{ – \pi }^\pi {{f^2}\left( x \right)dx},}$$
نتایج زیر حاصل میشود:
$${\frac{1}{2}{\left( {\frac{{2d}}{\pi }} \right)^2} + \sum\limits_{n = 1}^\infty {{{\left[ {\frac{{2\sin nd}}{{n\pi }}} \right]}^2}} }={ \frac{2}{\pi }\int\limits_0^\pi {{f^2}\left( x \right)dx} ,\;\;}\\ {\frac{{2{d^2}}}{{{\pi ^2}}} + \frac{4}{{{\pi ^2}}}\sum\limits_{n = 1}^\infty {\frac{{{{\sin }^2}nd}}{{{n^2}}}} }={ \frac{2}{\pi }\int\limits_0^d {dx} ,\;\;}\\ {\frac{{{d^2}}}{\pi } + \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{{\sin }^2}nd}}{{{n^2}}}} = d,\;\;}\\ {\frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{{\sin }^2}nd}}{{{n^2}}}} }={ d – \frac{{{d^2}}}{\pi },\;\;}\\ {\sum\limits_{n = 1}^\infty {\frac{{{{\sin }^2}nd}}{{{n^2}}}} }={ \frac{{d\left( {\pi – d} \right)}}{\pi } \cdot \frac{\pi }{2},\;\;}\\ {\sum\limits_{n = 1}^\infty {\frac{{{{\sin }^2}nd}}{{{n^2}}}} = \frac{{d\left( {\pi – d} \right)}}{2}.}$$
پس حاصل سری اول مشخص شد. برای محاسبه سری دوم از روابط مثلثاتی استفاده میکنیم:
$${\sum\limits_{n = 1}^\infty {\frac{{{\cos^2}nd}}{{{n^2}}}} } = {\sum\limits_{n = 1}^\infty {\frac{{1 – {\sin^2}nd}}{{{n^2}}}} } = {\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} – \sum\limits_{n = 1}^\infty {\frac{{{\sin^2}nd}}{{{n^2}}}} .}$$
ترم اول از عبارت سمت راست، در مثال اول محاسبه شد، با جایگذاری به نتیجه زیر میرسیم:
$${\sum\limits_{n = 1}^\infty {\frac{{{\cos^2}nd}}{{{n^2}}}} } = {\frac{{{\pi ^2}}}{6} – \frac{{d\left( {\pi – d} \right)}}{2} } = {\frac{{{\pi ^2} – 3\pi d + 3{d^2}}}{6}.}$$
همانطور که در سه مثال حل شده مشاهده کردیم، با استفاده از رابطه پارسوال میتوان حاصل بسیاری از سریها را محاسبه کرد. درحالیکه به روش مستقیم یا با تکنیکهای دیگر امکان محاسبه آنها وجود ندارد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- آموزش های پردازش سیگنال
- آموزش تجزیه و تحلیل سیگنال ها و سیستم ها
- مجموعه آموزشهای دروس مشترک رشته های فنی
- آموزش معادلات دیفرانسیل به همراه حل نمونه سئوالات آزمون کارشناسی ارشد
- تبدیل فوریه (Fourier Transform) — به زبان ساده
- انتگرال و مشتق سری فوریه — به زبان ساده
- راهنمای ضمیمه آموزش پردازش سیگنال با متلب
^^











با عرض سلام و احترام و تقدیر ئ تشکر. بسیار عالی بود و از آن استفاده کردیم. مطالب را بسیار شیوا و واضح مطرح فرموده اید. خدانگهدارتان