معادلات میدان اینشتین – توضیح و پاسخ ها به زبان ساده
معادلات میدان اینشتین (Einstein's Field Equations | EFE) معادلات حاکم بر نظریه نسبیت عام هستند. مهمترین مفاهیم تعریف شده در نسبیت عام، توسط این معادلات به یکدیگر مربوط میشوند. ذکر این نکته مهم است که معادلات میدان اینشتین به شکل یک معادله کلی نوشته میشوند. بنابراین، در نگاه نخست اینگونه به نظر میرسد که با یک معادله روبرو هستیم، تا چند معادله. اما نکته مهم آن است که چند معادله در یک معادله جمع شدهاند. در این مطلب، با معادلات میدان اینشتین در حالت کلی آشنا میشویم. همچنین، برای درک بهتر این معادلات، ریاضیات حاکم بر نسبیت عام، به زبان ساده توضیح داده میشوند.
- میآموزید تانسورها، متریک و کریستوفل چگونه در معادلات اینشتین بهکار میروند.
- خواهید آموخت تفسیر انرژی، جرم و خمیدگی فضا-زمان در تانسورهای کلیدی چیست.
- یاد میگیرید اصول هندسی و ریاضی چگونه مسیر حرکت اجسام را تعیین میکنند.
- با کاربرد عملی معادلات میدان اینشتین در مثالهای فیزیکی و کیهانشناسی آشنا میشوید.
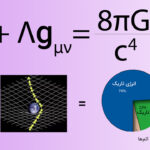
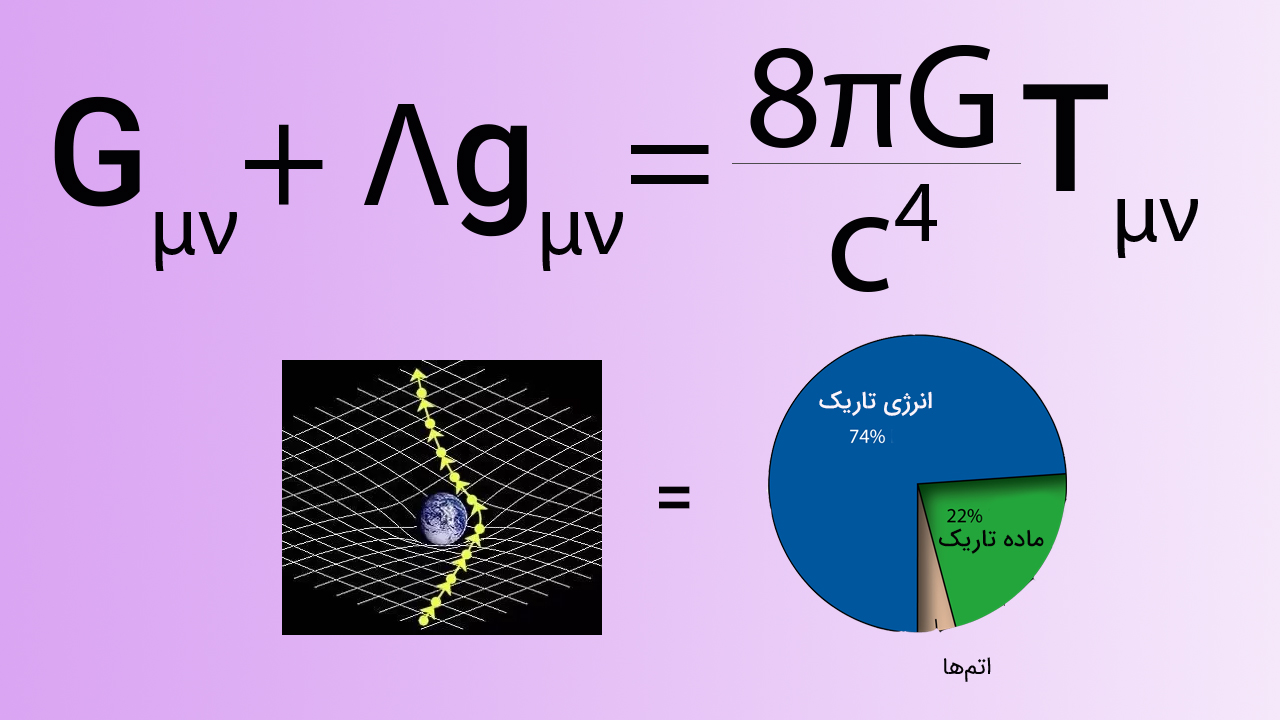
معادلات میدان اینشتین چیست ؟
مفاهیم بنیادی در نسبیت عام، توسط معادلاتی به نام معادلات میدان اینشتین، به یکدیگر مربوط میشوند. این معادلات به شکل کلی زیر نوشته میشوند:
شاید این سوال برایتان پیش بیاید که چرا این معادلات به صورت یک معادله نشان داده میشوند. معادلهای که در بالا مشاهده میکنید، راهی رایج برای نوشتن چندین معادله به صورت یک معادله است. اندیسهای و میتوانند مقدارهای عددی مختلفی داشته باشند. بنابراین، برای هر مقدار از و ، معادله مشخصی داریم:
قبل از آنکه در مورد هر قسمت از معادلات میدانی اینشتین صحبت کنیم، باید بدانیم که کمیتی به نام تانسورها در این معادلات، نقش اصلی را ایفا میکنند. به بیان دیگر، و و ، تانسور هستند. در ادامه، در مورد تانسور صحبت خواهیم کرد. نکته جالب در مورد تانسورها آن است که میتوانند به شکل ماتریسی، نمایش داده شوند.
به طور حتم، با ماتریسها آشنا هستید. ماتریسها به شکل زیر نوشته میشوند:
ماتریس و تانسور
ماتریسها حاوی اطلاعات مشخصی هستند. مطلب را با ذکر مثالی، ادامه میدهیم. فرض کنید پنج سبدِ سیب داریم. سه سیب به رنگهای زرد، قرمز و سبز، در هر سبد قرار گرفتهاند. هر سبد و همچنین سیبهای داخل هر سبد را به ترتیب، از یک تا پنج و از یک تا سه، شمارهگذاری میکنیم:
- سیبهای قرمز: شماره یک
- سیبهای سبز: شماره دو
- سیبهای زرد: شماره سه
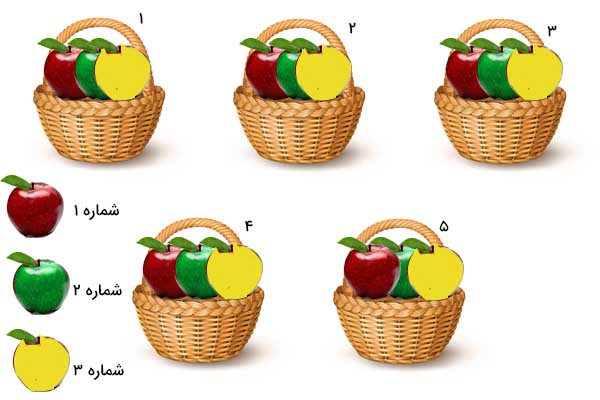
در ادامه، جرم هر یک از سیبها را بهدست میآوریم. جدول زیر، جرم هر سیب در هر سبد را نشان میدهد:
| سیب شماره ۱ | سیب شماره ۲ | سیب شماره ۳ | |
| سبد شماره ۱ | ۱۰۲ گرم | ۱۰۵ گرم | ۹۸ گرم |
| سبد شماره ۲ | ۹۹ گرم | ۱۰۵ گرم | ۹۹ گرم |
| سبد شماره ۳ | ۱۰۲ گرم | ۱۰۳ گرم | ۹۷ گرم |
| سبد شماره ۴ | ۹۸ گرم | ۱۰۲ گرم | ۹۷ گرم |
| سبد شماره ۵ | ۹۷ گرم | ۱۰۶ گرم | ۱۰۱ گرم |
اطلاعات نشان داده شده در جدول بالا را میتوانیم به شکل ماتریس نشان دهیم.
به ماتریس نوشته شده دقت کنید. هر ردیف در ماتریس، نشاندهنده یکی از سبدها است. به عنوان مثال، ردیف اول، نشاندهنده سبد شماره یک و ردیف سوم، نشاندهنده سبد شمار سه است. همچنین، هر یک از ستونها، نشاندهنده یکی از سیبهای قرمز، سبز یا زرد است. این ماتریس، جرم هر یک از سیبها در سبدها را نشان میدهد. به عنوان مثال، ردیف چهارم و ستون دوم از ماتریس، سیب سبز در سبد شماره چهار را نشان میدهد. جرم این سیب برابر ۱۰۲ گرم است.
ماتریس نوشته شده در بالا را میتوان به شکل مولفه ماتریسی نیز نشان داد. اطلاعات مختلف در مولفههای ماتریس ذخیره شده است. ماتریسِ سبدها و سیبهای داخل آنهای را با M نشان میدهیم. ماتریس M به شکل مولفهای به صورت زیر نوشته میشود:
مولفه مربوط به سیب قرمز در سبد شماره یک است و به طور مشابه، هر یک از مولفههای ماتریس، یکی از سیبها در یکی از سبدها را نشان میدهد. مولفه ماتریس M در حالت کلی به صورت نوشته میشود که در آن i بیانگر شماره سطر و j نشاندهنده شماره ستون است. مقدار i در ماتریس M بین یک تا پنج و مقدار j در آن، بین یک تا سه است.
همانطور که دیدیم، ماتریسها راه جالبی برای نشان دادن اطلاعات هستند. علاوه بر آن، ویژگیهای جالبی نیز دارند. رفتار تانسورها در معادلات میدان اینشتین بسیار شبیه رفتار ماتریسها است. بار دیگر به شکل ریاضی معادلات میدان اینشتین که در ادامه نوشته میشود، دقت کنید:
یا شما را به یاد چه چیزی میاندازد؟ مولفه ماتریس. تانسورهای به کار رفته در معادلات میدان اینشتین به شکل ماتریسهای ، چهار سطر و چهار ستون، نشان داده میشوند. در ماتریس M دیدیم که سطرها و ستونهای به ترتیب از یک تا پنج و یک تا سه شمارهگذاری شدهاند. اما شمارهگذاری ردیفها و سطرهای تانسورهای معادلات میدان اینشتین به جای شروع از یک، از صفر آغاز میشوند. بنابراین، مقدار اندیسهای و از صفر تا سه تغییر میکنند.
اعداد صفر، یک، دو و سه به چهار بعد مختلف استفاده شده در نسبیت مربوط میشوند.
- عدد صفر نشاندهنده بعد زمان است.
- اعداد یک، دو و سه نشاندهنده فضای سهبعدی هستند و گاهی با x و y و z نشان داده میشوند.
تا اینجا میدانیم که معادلات میدان اینشتین با تانسورهای نمایش داده میشوند. در ادامه، در مورد معنای هر یک از این تانسورها صحبت میکنیم.
معنای تانسورهای استفاده شده در معادلات میدان اینشتین چیست ؟
سه تانسور در معادلات میدان اینشتین استفاده شدهاند:
- تانسور
- تانسور
- تانسور
تانسور چیست ؟
، تانسور ضربه-انرژی است. این تانسور، حاوی اطلاعاتی در مورد توزیع ماده و انرژی در ناحیه فضا-زمانِ موردنظر است. هنگامی که در نسبیت در مورد ماده و انرژی صحبت میکنیم، به طور حتم معادله معروف اینشتین را به یاد خواهیم آورد:
بر طبق این معادله، ماده و انرژی معادل یکدیگر هستند. تانسور ضربه-انرژی در مورد چگونگی توزیع ماده و انرژی در ناحیهای از فضا و زمان که در نظر گرفتهایم، صحبت میکند. ناحیه موردنظر در بیشتر مواقع، تمام کیهان است. تانسور T_ {mu nu} به شکل زیر نوشته میشود:
به عنوان مثال، نشاندهنده چگالی انرژی یا چگالی تکانه است. این تانسور بسیار پیچیده است، اما در حالت کلی، چگونگی توزیع ماده و انرژی و حرکت انرژی در ناحیه موردنظر را نشان میدهد. اطلاعات کلی در مورد توزیع انرژی، توزیع جرم، شار تکانه و ... در تانسور ضربه-انرژی قرار گرفتهاند. این تانسور بسیار مهم است، زیرا به طور مستقیم به خمیدگی فضا-زمان مربوط میشود. خمیدگی فضا-زمان در نزدیکی اجسام کلانجرم یکی از مشخصههای اصلی نسبیت عام است. فضا-زمان بدون حضور جرم یا انرژی، تخت است. حال اگر جسمی مانند خورشید یا مقدار زیادی انرژی به این فضای تهی وارد شود، فضا-زمان در آنجا، خمیده خواهد شد. تا اینجا میدانیم، تانسور در مورد توزیع انرژی و جرم صحبت میکند. در ادامه، به تانسور مهم دیگری به نام تانسور اینشتین، ، میرسیم.
تانسور چیست ؟
تانسور ، تانسور اینشتین نام دارد. این تانسور حاوی اطلاعاتی در مورد خمیدگی فضا-زمان در حضور جرم سنگین یا مقدار انرژی زیاد است. به بیان دیگر، معادلات میدان اینشتین به ما میگوید که چگونگی توزیع جرم و انرژی در فضا-زمان، به خمیدگی فضا-زمان میرسد. به طور معادل، این معادلات توضیح میدهد که چگونه فضا-زمانِ خمیده سبب رفتار جرم و انرژی در ناحیه موردنظر از فضا-زمان میشود. خمیدگی فضا-زمان همان چیزی است که به عنوان گرانش میشناسیم.
معادلات میدان اینشتین به طور کامل، موردهای گفته شده در بالا را پوشش میدهد. با حل این معادلات، مقدار انرژی یا جرم لازم برای خمیدگی فضا-زمان به شکل مشخص را بهدست میآوریم. در نتیجه، رفتار جسم در فضا-زمان خمیده را مطالعه میکنیم. تانسور ، تابعی پیچیده از تانسورهای دیگر، مانند تانسور ریچی، است. تانسور ریچی، اطلاعاتی در مورد تفاوت فضا-زمان خمیده با فضا-زمان تخت به ما میدهد. همچنین، تانسور اینشتین تابعی از تانسور متری (متریک)، ، است. تانسور متری، تانسور بسیار مهمی در نسبیت عام است.
تانسور چیست ؟
، تانسور متری نام دارد و در مورد شکل فضا-زمان صحبت میکند. مورچهای را فرض کنید که در صفحه دوبعدی یا صفحهای تخت، زندگی میکند. این مورچه تنها میتواند به عقب، جلو، راست یا چپ، حرکت کند. دو نقطه دلخواه در این صفحه را انتخاب و آنها را A و B مینامیم. مورچه میخواهد از نقطه A به نقطه B برود.

کوتاهترین مسیر از A به B، خط مستقیمِ متصلکننده این دو نقطه است. فضا-زمان تخت به این صورت توصیف میشود. در فضا-زمانِ تخت، هیچ جرم و انرژی قرار ندارد تا آن را خمیده کند. اکنون فرض کنید سطحی که مورچه روی آن قرار دارد به گونهای خمیده میشود. حرکت مورچه در این حالت نیز تغییری نکرده است و تنها میتواند به چپ، راست، جلو، عقب یا ترکیبی از جهتهای مختلف، حرکت کند.

همانند حالت قبل، مورچه از نقطه A به نقطه B حرکت میکند. کوتاهترین مسیر در این حالت چه مسیری است؟ مسیر خمیده. اگر مورچه بخواهد روی خط مستقیم از نقطه A به نقطه B برود، باید از کرمچاله بگذرد.
ثابت در معادلات میدان اینشتین چیست ؟
گفتیم تانسور ، تابعی از تانسور متری، است. سوالی که ممکن است مطرح شود آن است که اگر این دو تانسور به یکدیگر وابسته هستند، چرا در معادلات میدان اینشتین، جدا از یکدیگر نوشته شدهاند. دلیل این موضوع به ثابت که در کنار نوشته شده است، مربوط میشود. ثابت ، ثابت کیهانی نام دارد. گفتنیهای زیادی در مورد این ثابت وجود دارد. به طور خلاصه، این ثابت نشان میدهد کیهان به طور پیوسته با نرخ افزایشی، منبسط میشود. کهکشانهایی که در فاصله دورتری نسبت به زمین قرار گرفتهاند با سرعت بیشتری نسبت به کهکشانهای نزدیکتر به زمین، دور میشوند.
شواهد زیادی مبنی بر انبساط کیهان در فضا-زمان وجود دارد، اما نکته مهم آن است که سرعت این انبساط به طور پیوسته در حال افزایش است. از اینرو، علامت ثابت کیهانی در معادلات میدان اینشتین، مثبت در نظر گرفته میشود. به بیان دیگر، علامت مثبت نشاندهنده انبساط کیهان است. سرگذشت ثابت کیهانی بسیار عجیب است. در ابتدا، اینشتین معادلاتی میدانی خود را بدون در نظر گرفتن ثابت کیهانی نوشت. سپس، این ثابت را در معادلات خود قرار داد. در ادامه، اینشتین، گنجاندن ثابت کیهانی را بزرگترین اشتباه خود دانست، اما براساس نتایج تجربی مشاهده شده به این نتیجه رسید که ثابت کیهانی باید در معادلات میدانی قرار داشته باشد.
ثابت در معادلات میدان اینشتین چیست ؟
از چند ثابت آشنا تشکیل شده است:
- عدد
- G: ثابت جهانی گرانشی
- c: سرعت نور
این ثابت به ما میگوید چه مقدار انرژی در تانسور ضربه-انرژی برای خمیدگی فضا-زمان، لازم است. به بیان دیگر، این ثابت در مورد مقدار اثر انرژی و جرم بر مقدار خمیدگی فضا-زمان صحبت میکند.
تاکنون، با معادلات میدان اینشتین به زبان ساده آشنا شدیم. در این معادلات، شکل و انحنای فضا-زمان به توزیع جرم و انرژی در فضا-زمان، مربوط میشوند. همچنین، به دلیل ثابت کیهانی استفاده شده در این معادلات به این نتیجه میرسیم که کیهان با نرخ افزایشی، منبسط میشود. به این نکته توجه داشته باشید که حل معادلات میدان اینشتین بسیار مشکل است، اما برخی از معادلات با استفاده از شبیهسازیها و تقریبهای انجام شده، حل شدهاند:
- فضا-زمان تخت یا فضای مینکوفسکی: اگر در ناحیهای از فضا-زمان، جرم و انرژی وجود نداشته باشد، فضا-زمان در آن ناحیه، تخت خواهد بود.
- فضای شوارتزشیلد: سیاهچاله ثابت و انحنای فضا-زمان اطراف آن را توصیف میکند.
- فضای کِر: سیاهچاله چرخان و انحنای فضا-زمان اطراف آن را توصیف میکند.
ریاضیات معادلات میدان اینشتین
تاکنون با معادلات میدان اینشتین و هر قسمت از آن، آشنا شدیم. حل این معادلات بسیار سخت است و تنها برخی از آنها حل شدهاند. برای حل این معادلات باید با ریاضیات حاکم بر نسبیت عام آشنا باشیم. به همین دلیل، ریاضیات استفاده شده در نسبیت عام را به طور خلاصه توضیح میدهیم. برای داشتن درک بهتری از ریاضیات حاکم بر نسبیت عام، آن را به بخشهای مختلفی تقسیم کردهایم و به ترتیب در مورد آنها و سپس ترکیب هر بخش با بخش دیگر صحبت خواهیم کرد.
تانسور چیست ؟
به طور حتم، در فیزیک دبیرستان با مفهومی به نام بردار آشنا شدهاید. بردار با پیکان نشان داده میشود و دو ویژگی مهم دارد:
- اندازه: طول پیکان، نشاندهنده جهت بردار است.
- جهت: جهت پیکان، جهت بردار را نشان میدهد.
نیروی جاذبه، شتاب و سرعت، مثالهایی از کمیتهای برداری هستند. بردارها، کمیتهای دیگری مانند مساحت را نیز نشان میدهند. چگونه بردار، مساحت را نشان میدهد؟ پاسخ به این پرسش، بسیار ساده است. طول بردار را متناسب با مساحت ناحیه موردنظر و جهت بردار را عمود بر صفحه موردنظر قرار میدهیم. بردارها، کمیتهای بسیاری را نشان میدهند. اگر میخواهید فراتر از تعریف بردار گام بردارید و بردارها را به عنوان اعضای گروه بزرگتری به عنوان تانسورها در نظر بگیرید، باید با دو مفهوم مولفههای برداری و بردارهای پایه آشنا باشید.
مولفه های برداری
برای داشتن درک بهتری از مولفههای برداری، ابتدا دستگاه مختصاتی به شکل زیر در نظر بگیرید. به این دستگاه مختصات، دستگاه مختصات دکارتی گفته میشود. همانطور که در تصویر زیر مشاهده میشود، محورهای x و y و z، دو به دو بر یکدیگر عمود هستند. نکته مهم در مورد دستگاههای مختصات مختلف (دستگاه مختصات دکارتی، کروی یا استوانهای)، بردارهای پایه است.
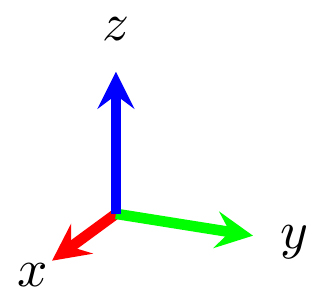
اندازه بردارهای پایه برابر یک است. همچنین، جهت این بردارها، در جهت محورهای مختصات است. بردارهای پایه در دستگاه مختصات دکارتی به صورت زیر نوشته میشوند:
- بردار پایه در راستای محور x، با یا نشان داده میشود.
- بردار پایه در راستای محور y، با یا نشان داده میشود.
- بردار پایه در راستای محور z، با یا نشان داده میشود.
با داشتن دستگاه مختصات مناسب و بردارهای پایه، مولفههای بردار موردنظرتان را میتوانید بهدست آورید. برای به دست آوردن مولفههای برداری دلخواه به صورت زیر عمل میکنیم:
- برای بهدست آوردن مولفه بردار در راستای محور z، تصویر بردار را روی این محور بهدست میآوریم. برای انجام این کار، از انتهای بردار، خطی موازی صفحه xy رسم میکنیم. محل تقاطع این خط را با محور z بهدست میآوریم و مبدأ مختصات را به محل تقاطع وصل میکنیم.
- برای بهدست آوردن مولفه بردار در راستای محور x، از انتهای بردار خطی موازی محور z و عمود بر صفحه xy رسم میکنیم و محل تقاطع خط را با صفحه xy بهدست میآوریم. در ادامه، مبدأ مختصات را به نقطه تقاطع وصل میکنیم.
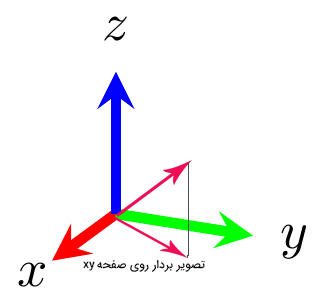
- برای بهدست آوردن مولفه بردار در راستای محور x، از تصویر بردار در صفحه xy استفاده میکنیم. برای انجام این کار، از انتهای بردار، خطی موازی محور y رسم میکنیم. محل تقاطع این خط را با محور y بهدست میآوریم و مبدأ مختصات را به محل تقاطع وصل میکنیم.
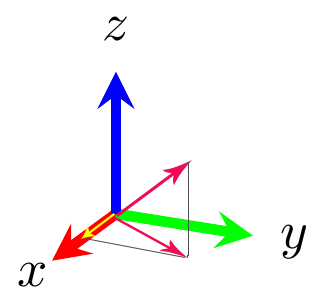
- برای بهدست آوردن مولفه بردار در راستای محور y، از تصویر بردار در صفحه xy استفاده میکنیم. برای انجام این کار، از انتهای بردار، خطی موازی محور x رسم میکنیم. محل تقاطع این خط را با محور x بهدست میآوریم و مبدأ مختصات را به محل تقاطع وصل میکنیم.
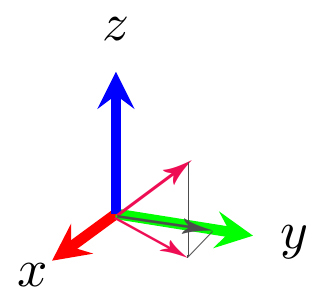
تاکنون، با چگونگی بهدست آوردن مولفههای بردار در راستای سه محور مختصات آشنا شدیم. در ادامه، مولفههای بردار را برحسب بردارهای پایه در هر راستا مینویسیم. فرض کنید برداری به نام A را به مولفههایش در راستای محورهای x و y و z، تجزیه کردهایم و آنها را به ترتیب و و مینامیم. بنابراین، بردار A به صورت زیر نوشته میشود:
هر یک از مولفههای و و ، یک اندیس دارند، زیرا تنها یک مولفه بردار واحد برای هر جزء وجود دارد. توجه به این نکته مهم است که اندازه بردارهای پایه در هر راستا، واحد و برابر یک است. بنابراین، بردارها، تانسور مرتبه یک هستند. همچنین، کمیتهای نردهای به عنوان تانسورهای مرتبه صفر شناخته میشوند. در ادامه، با تانسورهای مرتبه بالاتر آشنا میشویم. تانسور مرتبه دو در فضای سهبعدی در تصویر زیر نشان داده شده است. تانسور مرتبه یک، بردار، از سه مولفه و سه بردار پایه تشکیل میشود. در مقابل، تانسور مرتبه دوم از نه مولفه و ۹ دسته دوتایی بردار پایه تشکیل شده است.

شاید از خود بپرسید چرا تانسور مرتبه دو به این صورت نشان داده میشود. به عنوان مثال، نیروهای داخلی جسمی جامد را در نظر بگیرید. این جسم جامد از سطوح مختلفی تشکیل شده که بردار سطح آنها در راستای محورهای x یا y یا z قرار گرفته است. همچنین، روی هر یک از این سطوح ممکن است نیرویی وجود داشته باشد که مولفه آن در راستای محورهای x یا y یا z باشد. بنابراین، برای تحلیل تمام نیروهای وارد شده بر تمام سطوح جسم جامد، به نه مولفه با دو اندیس (هر اندیس به یک بردار پایه اشاره دارد) نیاز داریم. به عنوان مثال، نشاندهنده نیرویی در راستای محور x، روی سطحی است که بردار سطح آن در راستای محور x قرار دارد. همچنین، نشاندهنده نیرویی در راستای محور x، روی سطحی است که بردار سطح آن در راستای محور y قرار دارد.
سوالی که ممکن است مطرح شود آن است که چرا از ترکیب مولفهها و بردارهای پایه، تانسورها به عنوانی عناصری بسیار قوی در فیزیک و ریاضی ساخته میشوند؟ زیرا، تمام ناظرها در تمام چارچوبهای مرجع، تنها در مورد ترکیب بردارهای پایه با مولفهها، یا همان تانسورها، به توافق رسیدهاند.
فضا-زمان و خط جهانی
میزی را در نظر بگیرید که کاغذی روی آن قرار دارد. نموداری دلخواه روی کاغذ رسم میکنیم. ورقه کاغذ، تصویری از ساختار کیهان (فضا-زمان) است. فضا-زمان، چهار بعد دارد، اما برای سادگی تنها دو بعد از چهار بعد نمایش داده میشوند. نمودار رسم شده روی کاغذ، جسمی مانند سیب را توصیف میکند. به این نمودار، خط جهانی میگوییم و به دنبال توصیف آن هستیم. برای انجام این کار، خط جهانی را به قسمتهای کوچکتر و مساوی تقسیم میکنیم. یکی از این نقاط را به عنوان نقطه مرجع یا مبدأ، انتخاب و نقطههای دیگر را با توجه به نقطه انتخاب شده، شمارهگذاری میکنیم. در این حالت، نموداری تقسیمبندی شده داریم که به ما اجازه میدهد آن را به مجموعهای از نقطههای متوالی تبدیل کنیم. این نقطهها میتوانند به عنوان مسیر حرکت، در نظر گرفته شوند.
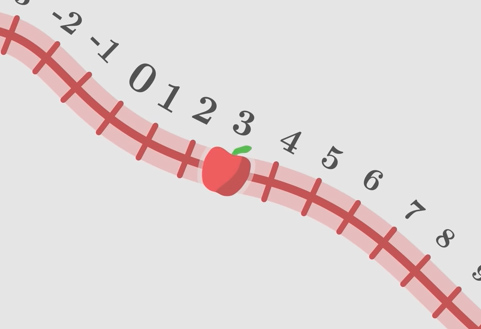
بنابراین، نمودار، دیگر جسمی مانند سیب نیست، بلکه مسیر حرکت است و حرکت سیب را در فضا-زمان نشان میدهد. از اینرو، مفهوم حرکت را اختراع کردهایم. این نقاط تقسیمبندی شده روی نمودار که سیب در امتداد آنها حرکت میکند، زمان ویژه سیب نام دارد. زمان ویژه سیب، زمانی است که تکامل درونی سیب را نشان میدهد. به بیان دیگر، گذر این زمان مطابق با ساعت سیب است. با گذشت زمان، سیب در بعدِ فضا-زمان حرکت میکند. زمان ویژه را با حرف یونانی نشان میدهیم. به این نکته توجه داشته باشید که زمان ویژه توسط ساعتی اندازه گرفته میشود که نسبت به جسم ساکن است. در مثالِ سیب، ساعت درونی سیب، نسبت به آن ساکن است.
در ادامه، میخواهیم موقعیت مکانی سیب را با گذشت زمان ویژه نشان دهیم. برای آنکه بتوانیم نقطهای را به صورت ریاضی مشخص کنیم، دستگاه مختصاتی روی صفحه رسم میکنیم. این دستگاه مختصات، به صورت توری نشان داده میشود. مبدأ این توری را نقطه صفر در نظر میگیریم و همانطور که در تصویر زیر نشان داده شده است، با حرکت به سمت بالا، پایین، چپ یا راست، نقطههای تقاطع را یکییکی شمارهگذاری میکنیم. در این حالت، موقعیت سیب در صفحه، توسط دو نقطه به نام مختصات سیب، توصیف میشود. به عنوان مثال، مختصات سیب در تصویر نشان داده شده برابر است. توجه به این نکته مهم است که توری رسم شده، کاملا دلخواه است و هیچ معنای فیزیکی ندارد و تنها قراردادی است که انتخاب میکنیم.
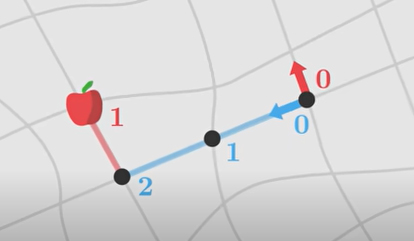
انتخاب مختصات بستگی به چگونگی توصیف ما از موقعیت سیب دارد. بنابراین، در موقعیتهای مختلف، سیستمهای مختصاتی متفاوتی استفاده میشوند و در انتخاب هر یک از آنها آزاد هستیم. در ادامه، مفاهیم مطرح شده را با ذکر مثال توضیح میدهیم. سیبی را در نظر بگیرید که در فاصله مشخصی از سطح زمین قرار دارد و به صورت عمودی به سمت زمین سقوط میکند. فرض کنید، سیستم سیب و زمین را از فاصله بسیار دوری تماشا میکنیم. به این پرسش اندکی فکر کنید، به عنوان ناظری که در دوردست نشستهاید، چه کمیتهایی را میتوانید اندازه بگیرید؟ در ابتدا، فاصله بین زمین و سیب را میتوانید اندازه بگیرید. هنگامی که سیب به صورت عمودی به سمت زمین سقوط میکند، فاصله آن از زمین کاهش مییابد.
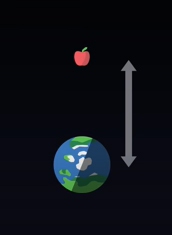
همچنین، میتوانیم زمان را با استفاده از ساعت خود اندازه بگیریم. زمان اندازهگیری شده در حالت کلی با زمان ویژه سیب، برابر نخواهد بود. در این حالت، دو مختصات تعریف میشود:
- زمان، که با t نشان داده میشود.
- ارتفاع، که با r نشان داده میشود.
با استفاده از این دو مختصات میتوانیم مکان سیب را در فضا-زمان نسبت به چشمانداز خود، تعیین کنیم. با گذشت زمان ویژه، سیب آزادانه حرکت میکند و مسیر خود در سیستم مختصات تعریف شده، دنبال میکند. به این نکته توجه داشته باشید که در اینجا دو زمان را تعریف کردیم. زمان ویژه که نسبت به ساعت درونی سیب اندازه گرفته میشود و زمانی که ناظر با ساعت خود اندازه میگیرد. فرض کنید سیب از نقطهای با مختصات یک ثانیه و ۷۰۰۰ کیلومتر، میگذرد. این جمله چه مفهومی در خود دارد؟ هنگامی که ساعت ما یک ثانیه را نشان میدهد، فاصله بین سیب و زمین از دید ما برابر ۷۰۰۰ کیلومتر است.
توجه به این نکته مهم است که هیچ جسمی در فضا-زمان ساکن نیست. شاید از خود بپرسید، سیبی که روی میز قرار دارد، هیچ حرکتی نخواهد کرد. این نکته را به یاد داشته باشید که هر جسمی در زمان حرکت میکند. به عنوان مثال، سیب با گذشت هر ثانیه، به سمت آینده حرکت میکند. همچنین، تمام اجسام در فضا-زمان، سرعت دارند. تنها عامل متغیر، چگونگی توزیع سرعت در مختصات فضا و زمان است.
سرعت در فضا-زمان
در مطالب بالا گفتیم، تنها عامل متغیر در فضا-زمان، چگونگی توزیع سرعت است. تا اینجا میتوانیم موقعیت سیب را توسط دو مختصات، مشخص کنیم. این مختصات به زمان ویژه بستگی دارد. همچنین، خط جهانی را به صورت حرکت با گذشت زمان ویژه، تعریف کردیم. در ادامه، در مورد مفهوم سرعت صحبت خواهیم کرد.
سرعت سیب در فضا-زمان به صورت برداری مماس بر مسیر حرکت آن تعریف میشود. جهت این بردار در راستای جهت حرکت سیب و اندازه آن نشاندهنده سرعت حرکت است. مقدار سرعت در همه جا یکسان است، زیرا خط جهانی به فاصلههای یکسانی تقسیم میشود. سیب همواره مسیر یکسانی را برای زمان ویژه داده شده، طی میکند.
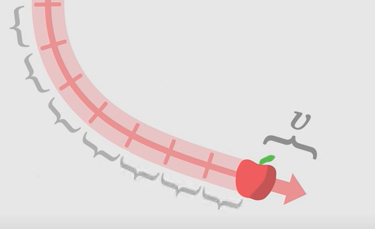
در حالت کلی، تمام اجسام موجود در کیهان با سرعت یکسانی حرکت میکنند. مقدار این سرعت، یکی از ثابتهای جهانی است و به آن سرعت نور، c، گفته میشود.
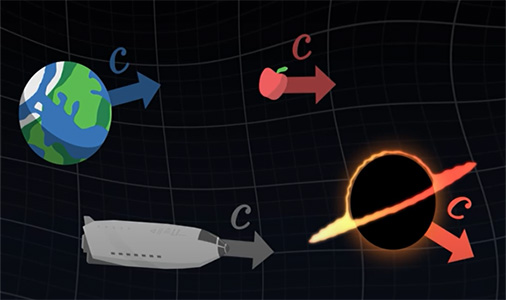
در ادامه، اولین معادله در نسبیت را مینویسیم. طول بردار سرعت، همواره برابر سرعت نور است.
هنگامی که از واحد منسجمی استفاده میکنیم، به عنوان مثال اندازهگیری زمان برحسب یک ثانیه و فاصله برحسب یک نور-ثانیه، سرعت نور به طور دقیق برابر یک میشود:
این بدان معنا است که زمان، اندازهگیری فاصله است. زمان ویژه جسم، فاصله طی شده در فضا-زمان را اندازه میگیرد. سیب در هر ثانیه از زمان ویژه، به اندازه یک نور-ثانیه در فضا-زمان حرکت میکند. در ادامه، سرعت را با استفاده از مختصات، توصیف میکنیم. به تصویر زیر دقت کنید. سیبی در شبکهای دلخواه قرار دارد. دو بردار آبی و قرمز نشان داده شده در تصویر نشاندهنده جهت و دامنه هر مختصات هستند. به این بردارها، بردارهای پایه گفته میشود و آنها را با و نشان میدهیم.
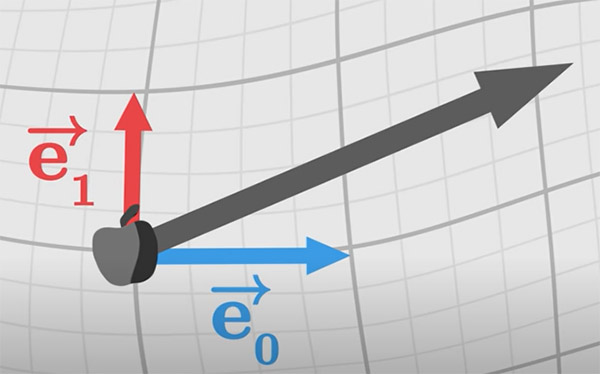
سرعت را میتوان برحسب این بردارهای پایه نوشت. در مطالب بالا با بردارهای پایه و مولفه بردار آشنا شدیم. به عنوان مثال، اگر بردار سرعت به صورت نوشته شود، ۱ و ۲ مولفههای بردار سرعت هستند. مقدارهای مولفه، نرخ افزایش مختصات موردنظر را نشان میدهند. به عنوان مثال، با دانستن مولفه بردار سرعت، نرخ حرکت سیب در هر مختصات را با گذشت زمان ویژه بهدست میآوریم.
سرعت را به صورت زیر نوشتیم:
رابطه فوق را به صورت زیر، سادهتر و کوتاهتر مینویسیم:
سپس، حرف یونانی دلخواهی را جایگزین عدد صفر میکنیم. عددهای صفر و یک، نشاندهنده مختصات موردنظر هستند.
مقدار برابر صفر و یک است. این ساختار نوشتاری برای معادلهها در نسبیت عام، توسط اینشتین اختراع شد. هنگامی که حرف یونانی دو بار تکرار شود، یکبار بالا و یکبار پایین، جمع را نشان میدهد.
مثال
فرض کنید ماهوارهای در مدار دایرهای به دور زمین میچرخد. حرکت ماهواره از دید ناظری در دوردست، توسط دو مختصات توصیف میشود.
- زمانی که با ساعت خود اندازه میگیریم و آن را با t نشان میدهیم.
- زاویه که نشاندهنده موقعیت ماهواره به دور زمین است.
با نگاه به خط جهانی ماهواره، سرعت ماهواره را میتوانیم در هر نقطه رسم کنیم.
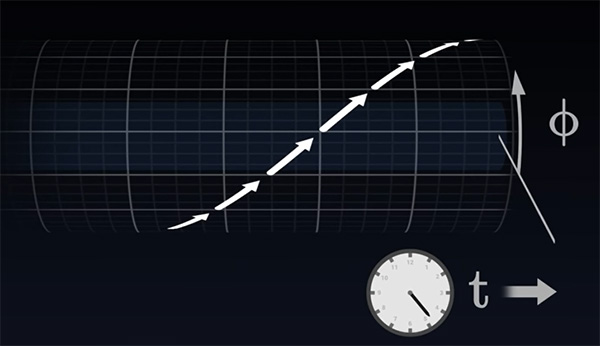
بردار سرعت را میتوان به دو مختصات موردنظر، تجزیه کرد:
- سرعت زمانی: این زمان برابر نرخ گذر زمان برای ناظر در مقایسه با زمان ویژه ماهواره است. مقدار آن را در این مثال برابر دو در نظر میگیریم. عدد دو بدان معنا است که هر یک ثانیه برای ماهواره، برابر دو ثانیه برای ناظر است. این سرعت را با نشان میدهیم.
- سرعت زاویهای: این سرعت نشاندهنده نرخ افزایش زاویه ماهواره به دور زمین است. به عنوان مثال، اگر مقدار این سرعت برابر ۱۰ درجه بر ثانیه باشد، برای هر یک ثانیه زمان ویژه، ماهواره ۱۰ درجه به دور زمین میچرخد. این سرعت را با نشان میدهیم.
نخستین رابطهای که نوشتیم را به یاد بیاورید. بر طبق این رابطه، طول بردار همواره ثابت است و به آن سرعت نور گفته میشود. شاید این سوال در ذهن شما شکل گرفته باشد، آیا میتوان با استفاده از قضیه فیثاغورث، سرعت نور را با استفاده از مولفههای آن بهدست آورد؟
توجه به این نکته مهم است که مختصات، فاصلههای واقعی را نشان نمیدهد. مقدار و نرخ تغییر آنها، اعداد دلخواهی هستند و هیچ معنای فیزیکی ندارند. به عنوان مثال، فرض کنید، دو ماهواره در مدارهای دایرهای با شعاعهای متفاوت، به دور زمین میچرخند. زاویههای شکل گرفته توسط این دو ماهواره با نرخ یکسانی افزایش مییابند. بنابراین، سرعت آنها مولفه زاویهای یکسانی دارد. اما این بدان معنا نیست که دو ماهواره با سرعت یکسانی حرکت میکنند. همانطور که میدانیم ماهواره دورتر، با سرعت بیشتری نسبت به ماهواره نزدیکتر حرکت میکند.
ژئودزیک
تا اینجا با مفاهیمی مانند خط جهانی و سرعت در فضا-زمان آشنا شدیم. در ادامه، در مورد تحول سرعت با گذشت زمان ویژه، صحبت میکنیم. با این کار، شکل مسیر حرکت را میتوانیم بهدست آوریم. در جهان ما، اجسام به طور طبیعی روی خط مستقیم حرکت میکنند. هنگامی که هیچ نیروی خارجی وارد نشود، خط جهانی در مختصات فضا-زمان، مستقیم است. دلیل این موضوع، تقارن چنین مسیری است. در واقع، جسم هیچ دلیلی برای خروج از خط مستقیم و انحراف به چپ یا راست ندارد. توجه به این موضوع به ما این امکان را میدهد که مسیر حرکت جسم را پیشبینی کنیم.
با دانستن سرعت حرکت جسم در لحظهای مشخص، بردار را در راستایی که نشان میدهد منتقل و حرکت جسم را پیشبینی میکنیم. به مسیر شکل گرفته از انتقال سرعت در راستای خود، ژئودزیک گفته میشود. تمام اجسام در جهان تمایل به دنبال کردن ژئودزیک دارند. بردار در ژئودزیک نمیچرخد. بنابراین، مشتق آن نسبت به زمان ویژه برابر صفر خواهد بود:
بردار سرعت سیب در امتداد ژئودزیک تغییر نمیکند.
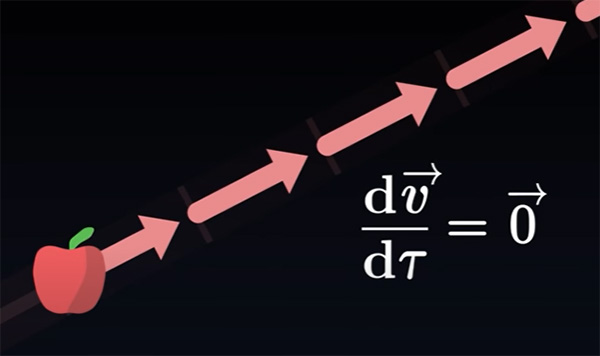
رابطه به ما میگوید حرکت طبیعی جسم، شتابدار نیست. بنابراین، هنگامی که نیرویی بر جسمی وارد نشود، به حرکت در راستای خط راست ادامه میدهد. در مطالب بالا دیدیم که بردار سرعت را میتوان برحسب حاصلضرب مولفههای آن در بردارهای پایه نوشت.
از رابطه بالا بر حسب زمان ویژه مشتق میگیریم و آن را برابر صفر قرار میدهیم.
با توجه به رابطه بالا، بین تغییرات مولفه سرعت و تغییرات بردار پایه رابطهای بهدست آمده است. بردار پایه در امتداد مسیر میتواند تغییر کند، زیرا شبکه انتخاب شده به عنوان دستگاه مختصات میتواند به طور کامل بینظم باشد. همچنین، گرچه بردار سرعت به عنوان جسمی هندسی، ثابت است، مولفههای آن میتوانند به هنگام حرکت سیب در شبکه انتخاب شده، تغییر کنند.
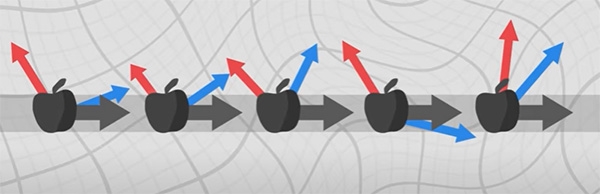
کمی عمیقتر در مورد تغییرات مولفههای بردار سرعت و بردارهای پایه صحبت میکنیم. تغییر بردار پایه در امتداد خط جهانی میتواند به صورت جمع حاصلضرب تغییرات آن در امتداد هر یک از محورهای مختصات در سرعت سیب، نوشته شود. زیرا هرچه سیب سریعتر حرکت کند، تغییر بردار پایه نیز سریعتر خواهد بود.
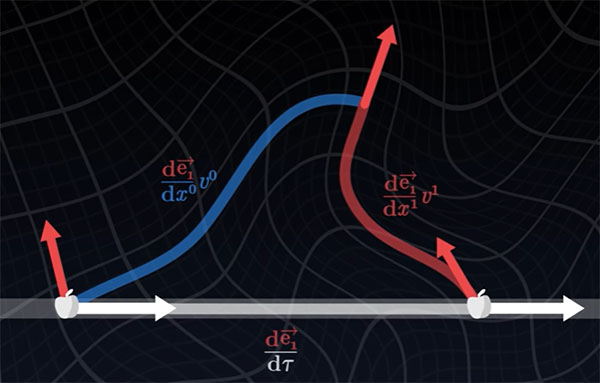
هر مختصات، کمیت جدیدی معرفی میکند که چگونگی تغییر بردار پایه در امتداد مختصات را نشان میدهد. این تغییر به صورت بردار مشتق بردار پایه برحسب مختصات، نشان داده میشود:
این بردار بسیار جالب است، زیرا به مسیر حرکت جسم بستگی ندارد و تنها به ساختار شبکه وابسته است. این بردار را برحسب مولفههایش به نام مینویسیم. با توجه به مطالب گفته شده در بالا، سیستم را دوبعدی در نظر میگیریم. برای این حالت، مولفه هشت حالت دارد، دو مولفه برای چهار بردار متفاوت. به اعداد نشان داده شده در تصویر، «نمادهای کریستوفل» (Christoffel Symbols) گفته میشود. این نمادها در نسبیت عام بسیار استفاده میشوند و کاربرد زیادی دارند. زیرا، نمادهای کریستوفل، تغییرات شبکه را در هر امتداد نشان میدهند و اطلاعات مهمی در مورد چگونگی رفتار شبکه دارند.
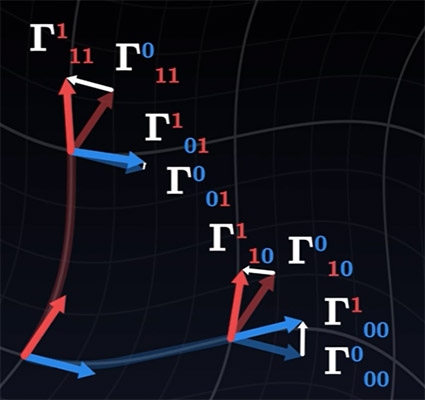
با نوشتن معادله را برحسب نمادهای کریستوفل، به معادله ژئودزیک میرسیم:
با استفاده از این معادله میتوان تغییر هر مولفه از سرعت را با گذشت زمان ویژه بهدست آورد. بنابراین، با استفاده از معادله ژئودزیک میتوان، تمام مسیر حرکت جسم را به درستی پیشبینی کرد. برای این کار تنها کافی است سرعت ذره در زمان داده شده و مقدار هر نماد کریستوفل را در سراسر شبکه بدانیم. برای درک بهتر این موضوع، به مثال زیر توجه کنید.
به جای فضا-زمان، زمین را در نظر میگیریم و سیستم مختصات طول و عرض جغرافیایی را برای آن انتخاب میکنیم. این انتخاب در نگاه اول بسیار مناسب به نظر میرسد. در ادامه، هواپیمایی را فرض میکنیم که در ارتفاع مشخصی از سطح زمین در راستای خط مستقیمی حرکت میکند. هنگامی که جسمی مستقیم و بدون انحراف حرکت میکند، به مسیر شکل گرفته توسط آن، ژئودزیک گفته میشود. در این مثال، ژئودزیک، دایرهای بزرگ به دور زمین است. هواپیما در این مسیر ژئودزیک همواره مستقیم و به سمت جلو حرکت میکند و جهت بردار سرعت آن تغییر نخواهد کرد. اما هنگامی که محورهای مختصات را روی زمین در نظر میگیریم، مسیر حرکت هواپیما به جای خط مستقیم، مسیری با انحنا به نظر میرسد. در واقع، اینگونه به نظر میرسد که جهت حرکت هواپیما در امتداد شبکه رسم شده، تغییر میکند. در واقعیت، مسیر حرکت هواپیما به طور کامل مستقیم است. نکته مهم در اینجا آن است که مشکل از هواپیما نیست، بلکه از شبکه انتخاب شده است. به بیان دیگر، دستگاه مختصات ما، منحنی است.
تانسور متریک
کمکم به مدل دقیقتری میرسیم. تاکنون، دستگاه مختصاتی برای توصیف مکان جسم ساختهایم. زمان ویژه را برای تفسیر خط جهانی در فضا-زمان، تعریف کردیم. همچنین، به معادلهای بنیادی در نسبیت عام به نام معادله ژئودزیک رسیدیم. با کمک این معادله و با استفاده از نمادهای کریستوفل میتوانیم مسیر حرکت جسم را پیشبینی کنیم. تا اینجا، پیشرفت خوبی حاصل شده، اما مشکل بزرگی هنوز باقی مانده است. گرچه دستگاه مختصات، نقاط را تعیین میکند، اما هیچ اطلاعاتی در مورد فاصله بین نقاط و زاویه بین آنها به ما نمیدهد. در واقع، فاصلهها و جهتها در شبکه در همهجا یکسان نیستند، بنابراین باید راهحلی برای این مورد ارائه شود.

برای انجام این کار، دو نقطه بسیار نزدیک به یکدیگر را روی کاغذ در نظر بگیرید. فرض میکنیم مختصات دو نقطه را میدانیم، بنابراین به دنبال راهی برای بهدست آوردن فاصله بین آنها هستیم. شاید، در نگاه اول به قضیه فیثاغورث فکر کرده باشید. و برابر تفاوتِ مختصات بین دو نقطه هستند.
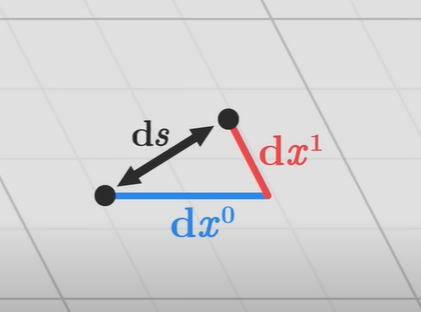
بنابراین فاصله بین دو نقطه، ، را شاید بتوان به صورت زیر نوشت:
اما مشکل بسیار مهمی وجود دارد. قضیه فیثاغورث را تنها میتوان هنگامی نوشته که خطها، سیستم مختصات عمودی، تشکیل دهند. اگر محورها بر یکدیگر عمود نباشند، از قضیه فیثاغورث نمیتوان استفاده کرد. بنابراین، باید از رابطه دیگری برای بهدست آوردن فاصله بین دو نقطه استفاده کنیم. توجه به این نکته مهم است که رابطه نوشته شده باید مستقل از شبکه مورد استفاده باشد. در حالت کلی، مجذور فاصله میتواند به صورت مجموع تمام حالتهای ممکن و ، نوشته شود:
به این نکته توجه داشته باشید که ضریبهای لزوما یک نیستند. مقدار این ضرایب، به طور مستقیم به شکل شبکه بستگی دارد. در حالتی که خطوط شبکه، مربعهایی به ضلع یک را تشکیل میدهند، ضرایب و برابر صفر و ضرایب و برابر یک هستند. در این حالت، به قضیه فیثاغورث برمیگردیم. ضرایب را میتوان در جدولی متشکل از یک سطر و یک ستون برای هر مختصات نوشت. به عنوان مثال اگر به صورت زیر نوشته شده باشد:
این ضرایب در جدولی به شکل نشان داده شده در تصویر، نوشته میشوند.

به این جدول، تانسور متری گفته میشود. این تانسور به شکل جدولی است که مولفههای آن به ما اجازه میدهند فاصلههای کوچک را اندازه بگیریم. به طور معمول، این جدول را با g نشان میدهیم و مولفههای آن را با دو اندیس، شمارهگذاری میکنیم.

بنابراین مجذور فاصله بین دو نقطه را میتوان به صورت زیر نوشت:
اینشتین رابطه طولانی بالا را به صورت زیر درآورد:
با استفاده از این فرمول، بزرگی سرعت را میتوانیم به صورت زیر بنویسیم. برای انجام این کار، را با مولفههای سرعت یعنی و جایگزین میکنیم:
در مطالب بالا گفتیم، بزرگی سرعت همواره برابر سرعت نور است. بنابراین، معادله بالا را میتوان به صورت زیر نوشت:
توجه به این نکته بسیار مهم است که تانسور متریک، کمیتی بنیادی و کلیدی در نسبیت عام است. قبل از تعریف تانسور متریک، تنها مختصات، اعداد انتزاعی و توصیفهای ریاضی داشتیم که کمیتهای واقعی را نشان نمیدانند. باید از تانسور متریک تشکر کنیم که توصیفهای انتزاعی را به اندازهگیریهای واقعی مکان و زاویه منتقل کرد. به بیان دیگر، تانسور متریک اعداد انتزاعی را به هندسه فیزیکی، مربوط میکند. معادله ژئودزیک را به یاد بیاورید:
گفتیم با کمک این معادله و با استفاده از نمادهای کریستوفل میتوانیم مسیر حرکت جسم را پیشبینی کنیم. اما سوالی که ممکن است مطرح شود آن است که مقدار هر نماد را چگونه میتوان بهدست آورد. در این نقطه، هیچ اطلاعی در مورد مقدار نمادهای کریستوفل نداریم، بنابراین از معادله ژئودزیک برای پیشبینی مسیر حرکت ذره نمیتوانیم استفاده کنیم. اما تانسور متریک به کمک ما آمد. با استفاده از این تانسور، مقدارهای نمادهای کریستوفل را میتوان محاسبه کرد. این نمادها نشان میدهند که چگونه بردارهای پایه در امتداد شبکه تغییر میکنند. اما بردارهای پایه به طور مستقیم متناسب با شکل شبکه هستند و شکل شبکه برحسب تانسور متریک بیان میشود. بنابراین، با اندازهگیری تغییر تانسور متریک در طول شبکه میتوان چگونگی تغییرات بردار پایه را بهدست آورد. در نتیجه، نمادهای کریستوفل محاسبه میشوند.
اکنون با دانستن نمادهای کریستوفل و با استفاده از معادله ژئودزیک میتوانیم مسیر حرکت ذره را پیشبینی کنیم. گفتیم نمادهای کریستوفل با تغییرات تانسور متریک، محاسبه میشوند. از اینرو، به رابطه زیر میرسیم:
معادله بالا، نمادهای کریستوفل را برحسب تغییرات تانسور متریک در امتداد شبکه بیان میکند. در معادله بالا معکوس تانسور متریک است که محاسبه آن بسیار سخت خواهد بود. در بیشتر حالتها، معادله بالا با انتخاب دستگاه مختصات مناسب، بسیار ساده نوشته میشود. به عنوان مثال، میتوان دستگاه مختصاتی را انتخاب کرد که محورهای آن بر یکدیگر عمود باشند. با انتخاب این دستگاه مختصات، معادله بالا به شکل سادهتر زیر نوشته میشود:
معکوس تانسور متریک در معادله بالا وجود ندارد. بنابراین، تا اینجا با دانستن تانسور متریک، نمادهای کریستوفل را بهدست میآوریم و با داشتن مقادیر این نمادها میتوانیم مسیر حرکت اجسام را با استفاده از معادله ژئودزیک، پیشبینی کنیم. این روش، تنها به هندسه فضا-زمان بستگی دارد. هندسه فضا-زمان با استفاده از تانسور متریک، مجسم میشود. تانسور متریک رابطه بین فاصلههای واقعی و مختصات ما را توصیف میکند. متاسفانه، هنوز روش مناسبی برای تعیین تانسور متریک وجود ندارد. در ادامه، در مورد رابطه بین تانسور متریک و خمیدگی و مقدار انرژی در فضا-زمان صحبت خواهیم کرد.
مثال تانسور متریک
زمین را در نظر بگیرید که توسط مختصات طول و عرض جغرافیایی توصیف میشود. تانسور متریک در سطح کره و با در نظر گرفتن این شبکه، به صورت نشان داده شده در تصویر زیر نوشته میشود.

R برابر شعاع زمین و زاویههای و ، مختصات عرضی و طولی هستند. با استفاده از این نوشتار میتوانیم تانسور متریک را در هر نقطه در امتداد کره بهدست آوریم. برای محاسبه این تانسور در هر نقطه، مقدارهای و را در آن نقطه جایگزین میکنیم. اگر بخواهیم فاصله هر نقطه نزدیک را از نقطه موردنظر اندازه بگیریم، تنها کافی است حاصلضرب هر جزء از جدول بالا در تفاوت مختصات را با یکدیگر جمع کنیم.
جمع بالا، مجذور فاصله بین دو نقطه را به ما میدهد. بنابراین، با استفاده از تانسور متریک تنها میتوانیم فاصلههای بسیار کوچک را اندازه بگیریم. اگر بخواهیم فاصله بسیار بزرگ را اندازه بگیریم، باید تانسور متریک را در تمام مسیر محاسبه کنیم. زیرا شکل شبکه ممکن است از نقطهای به نقطه دیگر تغییر کند. به زبان ریاضی، باید فاصله بین دو نقطه بسیار کوچک را بهدست آوریم و در ادامه، برای محاسبه تمام مسیر، از ds انتگرال بگیریم.
تانسور متریک ابزار بسیار قدرتمندی است. با استفاده از این تانسور میتوانیم فاصلههای واقعی را در سطح کرهای مانند زمین، بهدست آوریم. در ادامه، از تانسور متری در فضا-زمان واقعی استفاده میکنیم. برای انجام این کار، سادهترین مثال، یعنی فضای تهی یا خلأ، را در نظر میگیریم. فرض کنید، ماهوارهای در این فضا حرکت میکند. برای توصیف حرکت ماهواره، دو مختصات را برای فضا-زمان در نظر میگیریم:
- زمان: براساس ساعت ما اندازه گرفته میشود.
- مکان یا x: موقعیت ماهواره را در امتداد محور عمودی، اندازه میگیرد.
با گذشت زمان، ماهواره در امتداد مسیر مشخصی در فضا-زمان حرکت میکند. مقدار تانسور متریک در این فضا برابر است با:

تانسور متریک در خلأ بسیار ساده و مقدار آن مستقل از مکان نقطه است. به بیان دیگر، این تانسور در هر نقطه در فضا-زمان، یکسان خواهد بود. از آنجا که مقدار تانسور متریک در خلأ در شبکه ساخته شده تغییر نمیکند، مشتق آن برابر صفر است.
همچنین، مقدار تمام نمادهای کریستوفل نیز برابر صفر خواهد بود.
با قرار دادن مقدار نماد کریستوفل در معادله ژئودزیک داریم:
بنابراین، مولفه سرعت ماهواره، تغییر نمیکند. از اینرو، ماهواره در فضا-زمان دوبعدی در امتداد خط راست حرکت خواهد کرد. به تانسور متریک توصیفکننده فضای خلأ، تانسور «مینکوفسکی» (Minkowski) گفته میشود. این تانسور، فضا-زمانِ نسبیت خاص را توصیف میکند. دلیل سادگی تانسور مینکوفسکی، عدم وابستگی آن به شبکه انتخاب شده است. هندسه فضا-زمان در این حالت در سراسر شبکه یکسان خواهد بود.
اتساع زمان، اولین پیشبینی انجام شده با استفاده از این تانسور است. رابطه اندازه سرعت با مولفههایش را به یاد بیاورید.
معادله فوق را برای ماهواره استفاده میکنیم و مولفه زمانی سرعت را برحسب مولفه مکانی سرعت مینویسیم:
هرچه ماهواره سریعتر در فضا حرکت کند، مقدار بزرگتر خواهد بود. در واقع، هرچه ماهواره سریعتر حرکت کند، زمان ما نسبت به زمان ویژه آن، سریعتر میگذرد. بنابراین، هرچه جسمی سریعتر در فضا حرکت کند، زمان ویژه آن نسبت به زمان ناظر، کندتر خواهد گذشت. در نگاه نخست، تانسور متریک مینکوفسکی شاید بسیار ساده به نظر میرسد، اما این تانسور ویژگی بسیار منحصر به فردی دارد. یکی از مولفههای آن برابر ۱- است. عدد ۱- بسیار عجیب و یکی از واحدهای بنیادی کیهان است. این عدد به ما میگوید بعد فضا و زمان به طور بنیادی با یکدیگر تفاوت دارند.
مثال ماهواره را بار دیگر در نظر و فاصله آن از نقطهای در آینده در اندازه بگیرید. فرض کنید فاصله ماهواره از این نقطه برابر دو ثانیه نوری است. ي
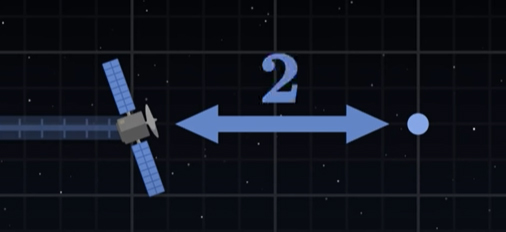
اگر نقطه موردنظر را در آینده به نقطه دیگری انتقال دهیم، انتظار فاصله بزرگتری را داریم. اما در واقع اینگونه نیست و فاصله کوتاهتر خواهد شد. دلیل این موضوع به عدد ۱- در تانسور متریک مینکوفسکی برمیگردد. هرچه انحراف نقطه در آینده بیشتر باشد، فاصله ماهواره از آن کمتر خواهد شد. این فاصله میتواند تا جایی کاهش یابد که فاصله موردنظر برابر صفر شود. به این حالت، نور گفته میشود.
خمیدگی
مدل ریاضی ما در حال کامل شدن است. در بخش قبل در مورد تانسور متریک صحبت کردیم. با استفاده از این تانسور میتوانیم، فاصلهها را در فضا-زمان اندازه بگیریم. مسیر حرکت جسم را میتوانیم با تعریف مختصات، سرعت و معادله ژئودزیک، پیشبینی کنیم. اما قدرت اصلی مدل ما آن است که هیچ فرضی در مورد هندسه فضا-زمان انجام نمیدهد. تا اینجا، صفحه حرکت سیب را مسطح در نظر گرفتهایم. سوالی که ممکن است مطرح شود آن است که اگر سطح موردنظر، خمیده باشد چه اتفاقی رخ خواهد داد. در این حالت نیز به راحتی میتوان، شبکه تعریف و مسیر حرکت جسم را پیشبینی کرد.
فضا-زمان همیشه مسطح و صاف نیست و هندسه آن میتواند خمیده باشد. انحنای فضا-زمان اثر جالبی بر مسیر حرکت جسم میگذارد. اگر فضا-زمان همانند کره، خمیده باشد، دو ژئودزیک موازی که از استوا شروع به حرکت به سمت شمال میکنند، به یکدیگر نزدیک خواهند شد. از این مدل برای گرانش استفاده میکنیم.

انحنای سطح کره، مفهومی کلیدی در نسبیت عام است و برای استفاده از آن به تعریف بسیار دقیقی نیاز داریم. صفحهای مربعی با شبکههای مربعی و کرهای با مختصات طولی و عرضی را در نظر بگیرید. دو بردار هماندازه و همجهت را روی این دو سطح، فرض کنید. در هر دو سطح، ابتدا بردار را به سمت بالا و سپس به سمت راست منتقل میکنیم. نتیجه انتقال بردارهای در هر سطح، در تصویر زیر نشان داده شده است.
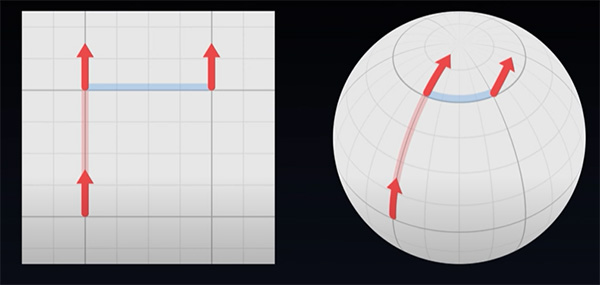
در ادامه، همان بردار را به نقطه مشابهی منتقل میکنیم، اما مسیر متفاوتی انتخاب میشود. ابتدا بردار را به سمت راست و سپس، آن را به بالا منتقل میکنیم. در صفحه، دو تصویر به دست آمده پس از انتقال بردار، یکسان هستند. به بیان دیگر، فرقی ندارد اول بردار را به سمت بالا و سپس به سمت راست منتقل کنیم یا ابتدا آن را به راست و سپس بالا، حرکت دهیم. اما دو تصویر نهایی در سطح کره با یکدیگر متفاوت خواهند بود و در جهتهای متفاوتی قرار میگیرند. به این اثر، خمیدگی گفته میشود.
برخی از صفحهها، مسطح است. در این صفحات، مسیر انتقال بردار بر تصویر نهایی آن تاثیر نمیگذارد. در مقابل، برخی از صفحات منحنی هستند و مسیر طی شده توسط بردار بر جهتگیری نهایی آن تاثیر میگذارد. تا اینجا، انحنا را به صورت مفهومی تعریف کردیم. در ادامه، آن را به صورت ریاضی بیان خواهیم کرد.
بردار پایهای روی سطح انتخاب و در ادامه، دو مختصات برای انتقال آن، انتخاب میکنیم. مختصات را به دو طریق میتوانیم انتخاب کنیم:
- مختصات یکسانی را دو بار انتخاب کنیم.
- دو مختصات متفاوت را انتخاب کنیم.
دو مختصات انتخاب شده را و مینامیم.
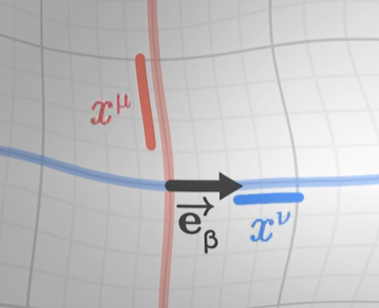
ابتدا بردار را در امتداد و سپس در امتداد منتقل میکنیم و به تصویر زیر میرسیم.
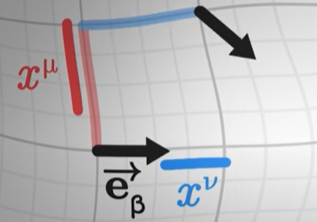
در ادامه، بردار را در امتداد و سپس در امتداد منتقل میکنیم و به تصویر زیر میرسیم.
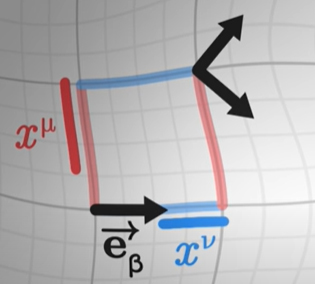
دو تصویر را با یکدیگر مقایسه کنید. دو تصویر متفاوت از بردار اول به دست آمده است. تفاوت بین این دو بردار با بردار جدیدی به نام R نشان داده میشود. اگر سطح مسطح و بدون هیچ انحنایی باشد، مقدار R برابر صفر خواهد بود. در مقابل، هر چه انحنای سطح بیشتر باشد، بردار R بزرگتر خواهد بود.
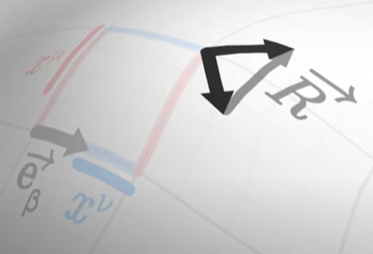
بردار R برابر تفاضل مشتق دو بردار پایه در جهتهای مخالف است. در حقیقت، بردار پایه را ابتدا در راستای و سپس منتقل میکنیم. در ادامه، آن را در راستای و سپس انتقال میدهیم.
در بخش قبل دیدیم، مشتق بردارهای پایه به ما نمادهای کریستوفل را میدهد.
نمادهای کریستوفل را در رابطه R قرار میدهیم:
با مرتبسازی رابطه بالا، به رابطه ساده شده زیر برای R میرسیم:
۱۶ حالت برای R وجود دارد. هر یک از این ۱۶ حالت، راهی برای انتقال بردار پایه روی سطح را نشان میدهد.
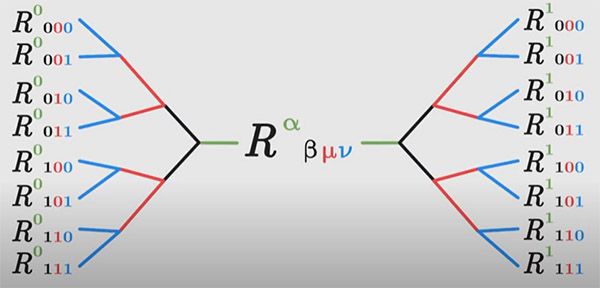
تانسور «انحنای ریمان» (Riemann curvature tensor) نام دارد. این تانسور به طور کامل، انحنای سطح را توصیف میکند. در مطالب بالا گفتیم، با دانستن تانسور متریک میتوانیم نمادهای کریستوفل را بهدست آوریم. در نتیجه، هر مولفه تانسور انحنا را میتوان محاسبه کرد. تانسور ریمان، انحنای فضا را در تمام جهتها مشخص میکند و ابزار کاملی برای توصیف هندسه است. توجه به این نکته مهم است که تعداد زیاد اجزای تانسور ریمان، استفاده از این تانسور را سخت کرده است. اما نباید ناامید شد، زیرا برخی از این اجزا، تکرار میشوند و مقدار برخی از آنها برابر صفر است. تعداد اجزای تانسور ریمان در فضای چهاربعدی حتی بیشتر و به ۲۵۶ میرسد.
باید دو ابزار برای توصیف انحنا معرفی کنیم به گونهای که استفاده از آنها در محاسبات سادهتر باشد. نخستین ابزار، تانسور ریچی نام دارد. این تانسور توسط جدولی متشکل از یک سطر و یک ستون برای هر مختصات، تعریف میشود. از آنجا که دو مختصات معرفی شده است، تعداد سطر و ستونهای جدول برابر دو خواهد بود.
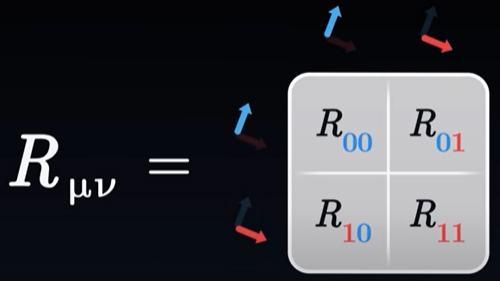
برای تعیین مقدار هر یک از مولفههای تانسور ریچی، به عنوان مثال مقدار ، از تانسورهای انحنا شروع میکنیم. از میان تمام مولفههای تانسور انحنا (۱۶ مولفه)، مولفهای را انتخاب میکنیم که اندیس دوم و چهارم آن برابر اندیسی است که میخواهیم بهدست آوریم (در اینجا اندیس صفر و یک مدنظر است). اگر بخواهیم مولفه را حساب کنیم، چهار مولفه از تانسور انحنا انتخاب میشوند:
از میان این چهار مولفه، مولفههایی را انتخاب میکنیم که اندیسهای اول و سوم آنها یکسان باشند.
در پایان، مولفههای باقیمانده را با یکدیگر جمع میکنیم.
به طور شهودی، تانسور ریچی، تغییرات حجم روی سطح را به هنگام حرکت روی آن، اندازه میگیرد. به عنوان مثال، در کره، حجم بین دو ژئودزیک موازی با پیشروی روی سطح، کاهش مییابد. مولفههای تانسور ریچی، این تغییرات حجم را در راستاهای مختلف سطح اندازه میگیرند. انحنا برای برخی سطوح متقارن مانند کره، در تمام جهتها یکسان است. بنابراین، میتوان آن را تنها با یک عدد بهدست آورد. این عدد متوسط انحنا را در تمام جهتها نشان میدهد. به این عدد، کمیت نردهای ریچی میگوییم. در حالتی که در دستگاه مختصات انتخاب شده، محورها بر یکدیگر عمود باشند، محاسبه کمیت نردهای ریچی بسیار آسان خواهد بود. این کمیت با استفاده از رابطه زیر بهدست میآید:
مثال های واقعی
فضای تهی یا خلأ را در نظر بگیرید. فضا-زمان را باز هم دوبعدی در نظر میگیریم. این فضا-زمان با استفاده از تانسور متریک مینکوفسکی توصیف میشود. همچنین، همانطور که گفته شد مولفههای این تانسور به مختصات بستگی ندارند و مقدار آن در تمام نقاط یکسان است. بنابراین، مشتق آن برابر صفر است. از اینرو، تمام نمادهای کریستوفل یکسان و مقدار آنها برابر صفر خواهد بود. در نتیجه، تانسورهای ریمان و ریچی و کمیت نردهای ریچی برابر صفر میشوند. فضا-زمان مینکوفسکی، تخت است و هیچ انحنایی ندارد. اگر دو جسم به صورت موازی شروع به حرکت کنند، هیچگاه به یکدیگر نخواهند رسید.
دومین مثال، کره است. نقطهای دلخواه روی کره توسط محورهای عرضی و طولی توصیف میشود. تانسور متریک برای چنین سطحی به صورت زیر نوشته میشود.
| 0 | ||
| 0 |
در این حالت، مقدار تانسور متریک در هر نقطه روی سطح یکسان نخواهد بود و مقدار آن به عرض جغرافیایی بستگی خواهد داشت. با محاسبه مشتقهای تانسور متریک برای کره، نمادهای کریستوفل بهدست میآیند. در ادامه، با دانستن مقدار نمادهای کریستوفل، مولفههای مختلف تانسور ریمان را بهدست میآوریم. سپس، تانسور ریچی و در پایان کمیت نردهای ریچی، محاسبه میشوند. انحنا در سطح کره، مثبت است. در نتیجه، دو ژئودزیک موازی به یکدیگر نزدیک خواهند شد. همچنین، با کاهش شعاع کره، مقدار انحنا نیز افزایش مییابد. هرچه کره بزرگتر باشد، سطح آن مسطحتر خواهد بود.
اکنون میدانیم تانسورهای متریک، ریمان و ریچی چه هستند و چگونه انحنای فضا-زمان را توصیف میکنند. در ادامه، در مورد شارهای انرژی صحبت خواهیم کرد.
شارهای انرژی
کیهان از فضا-زمان تشکیل شده است. فضا-زمان از ستارهها، جرم و اجسام بسیاری تشکیل شده است. در نگاه نخست، اجزای تشکلدهنده کیهان بسیار گوناگون و زیاد به نظر میرسند: سیارهها، ستارهها و ابرهای گرد و غبار میان ستارهای. این تنوع گسترده میتواند در مفهومی تک به نام انرژی خلاصه شود: حرکت انرژی. انرژی مفهومی انتزاعی است و وجود اختلال در کیهان را نشان میدهد. در حالت خاص، انرژی میتواند ناشی از جرم باشد. جرم بر طبق معادله ، حاوی انرژی است. اما فاکتورهای دیگری نیز، مانند انرژی تاریک یا میدان الکترومغناطیسی، نیز در انرژی موجود در جهان مداخله میکنند. توجه به این نکته مهم است که فشار انرژی تاریک، منفی است.
انرژی با هر شکلی، همانند سیال، در فضا-زمان حرکت میکند. به عنوان مثال، وجود سیب میتواند به صورت جریان انرژی، مدلسازی شود. برای توصیف آن، نقطهای را در مسیر حرکت در نظر بگیرید. در این نقطه، انرژی میتواند در جهتهای مختلف منتقل شود. در ورقه دوبعدی، انرژی میتواند از چهار جهت مختلف، دو جهت در امتداد هر مختصات، عبور کند.
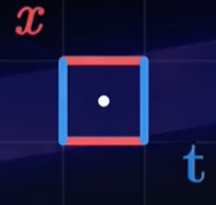
اگر انرژی در راستای مشخصی به نقطهای وارد شود، باید در همان راستا و در طرف مقابل، از نقطه خارج شود. بنابراین، برای توصیف کامل شارش انرژی، تنها به دو سطح نیاز داریم. اگر سیب در فضا-زمان بدون حرکت باشد، انرژی آن تنها برحسب زمان حرکت خواهد کرد. از اینرو، تنها سطح مرتبط با زمان با شار انرژی مواجه میشود. اگر سیب حرکت کند، سطوح زمان و فضا با شار انرژی مواجه خواهند شد. شار انرژی عبوری از هر سطح را با یک بردار نشان میدهیم. این بردارهای با توجه به رفتار انرژی میتوانند تغییر کنند. این بردارهای را برحسب مولفههایشان مینویسیم. این مولفهها را میتوان در تانسوری به نام تانسور انرژی-تکانه جا داد. این تانسور، نشاندهنده چگونگی انتقال تکانه در امتداد هر مختصات است. تانسور انرژی-تکانه با حرف T نشان داده میشود.
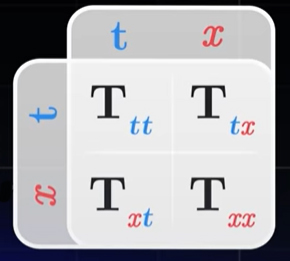
نخستین مولفه این تانسور، یعنی بیانگر مقدار انرژی منتقل شده در زمان است. این مولفه، مقدار انرژی عبوری از نقطهای که به سمت آینده حرکت میکند را نشان میدهد. به ، چگالی انرژی نیز گفته میشود. هرچه مقدار انرژی عبوری از نقطه موردنظر بیشتر باشد، اندازه نیز بزرگتر خواهد بود. دو کمیت دیگر یعنی، و با یکدیگر برابر هستند و مقدار انرژی عبوری در فضا برحسب زمان را نشان میدهند. هرچه انرژی سریعتر در فضا حرکت کند، مقدار این مولفهها بزرگتر خواهد بود. به این مولفهها چگالی تکانه گفته میشود.
مولفه آخر، یعنی ، مقدار حرکت در فضا را نشان میدهد. تفسیر این مولفه سخت است، زیرا باید معنایی برای عبارت «انتقال حرکت در فضا» بیابیم. در واقع، این مولفه تمایل انرژی به هل دادن در راستایی مشخص است و به آن فشار گفته میشود. تانسور T در فضای تعریف شده دوبعدی تنها چهار مولفه دارد. اما قضیه در جهان چهاربعدی ما، متفاوت خواهد بود. تعداد مولفههای تانسور T در فضای چهاربعدی برابر ۱۶ است و مولفههایی همانند چگالی انرژی، چگالی تکانه و فشار نیز دارد. اما توجه به این نکته مهم است که تعداد مولفههای چگالی تکانه در این حالت به ۶ و مولفه فشار به سه، افزایش یافته است. علاوه بر مولفههای گفته شده، مولفههای دیگری نیز در فضای چهاربعدی به تانسور T اضافه شدهاند: و و و و و . این مولفهها نشاندهنده گرانروی هستند. به تمایل انرژی برای انتقال حرکت خود به اطراف، گرانروی یا ویسکوزیته گفته میشود.
توجه به این نکته مهم است که مولفههای شارههای حرکت به مختصات انتخاب شده بستگی دارد. اگر مختصات را تغییر دهیم، انرژی ساکن میتواند به انرژی متحرک تبدیل شود. به بیان دیگر، حرکت نسبی است و به نقطه مشاهده یا به مکان ناظر بستگی دارد. برای داشتن درک بهتری از تانسور تکانه-انرژی، به دو مثال گفته شده در ادامه توجه کنید.
مثال اول همان فضا-زمان تهی یا خلأ است. نقطهای را فرض کنید که هیچ انرژی از آن عبور نمیکند. اگر تانسور تکانه-انرژی را برای این نقطه محاسبه کنیم، تمام مولفههای آن برابر صفر خواهند شد. فضای خلأ مثالی ساده، اما بنیادین است و در مثالها و حالتهای زیادی از آن استفاده میشود. هنگامی که میخواهیم حرکت جسم کوچکی را در فضا-زمان، مانند حرکت ماهواره به دور زمین یا سیبی نزدیک سیاهچاله، توصیف کنیم، به راحتی میتوانیم از انرژی جسم کوچک در برابر انرژی جسم بزرگتر، مانند زمین یا سیاهچاله، صرفنظر کنیم. به بیان دیگر، فرض میکنیم جسم کوچک در فضای خلأ قرار دارد و تانسور تکانه-انرژی آن برابر صفر است.
مثال دوم، داخل جسم است. به عنوان مثال، شاید در مورد رفتار جسم داخل خورشید کنجکاو باشیم. در این حالت، گرچه از جرم جسم کوچک صرفنظر میکنیم، اما نمیتوانیم آن را داخل خلأ فرض کنیم. زیرا باید مادهای که جسم کوچک در آن قرار گرفته است را حساب کنیم. در این حالت، تانسور تکانه-انرژی غیرصفر است. اگر فرض کنیم خورشیدی از سیالی ایدهآل با گرانروی صفر تشکیل شده است و در حالت تعادل قرار دارد، تانسور T تنها از چگالی انرژی وابسته به جرم خورشید و فشار درونی به سمت بیرون خورشید، تشکیل شده است.
تشکیل معادلات میدان اینشتین
تا اینجا در مورد مدل ریاضی استفاده شده در نسبیت عام صحبت کردیم. از یک سو میدانیم چگونه هندسه فضا-زمان و انحنای آن را توصیف کنیم. همچنین، با استفاده از معادلات ژئودزیک میتوانیم مسیر طبیعی اجسام را بهدست آوریم. برای انجام این کار، ابزارهای ریاضی مختلفی طراحی شده است:
- تانسور متریک
- نمادهای کریستوفل
- تانسور انحنای ریمان
- تانسور ریچی
- کمیت نردهای ریچی
همچنین، در مورد انرژی موجود در کیهان با استفاده از تانسور تکانه-انرژی صحبت کردیم. مهمترین ایده در نسبیت عام، معادل ساختن این دو ایده است.
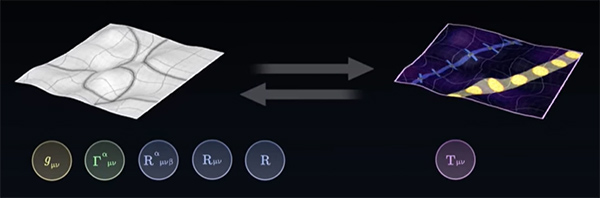
بنابراین، یکی از هدفهای اصلی نسبیت عام، برابر و معادل قرار دادن هندسه و محتوای کیهان است. اینشتین با نوشتن معادلات معروف خود با عنوان معادلات میدان اینشتین، این کار را انجام داد. این معادلات نمیتوانند اثبات شوند و بر طبق مشاهدات انجام شده، نوشته شدهاند. این معادلات به خوبی میتوانند جهان اطراف را توصیف کنند. در معادلات میدان اینشتین تمام پیشبینیهای انجام شده در نسبیت عام، وجود دارند. با استفاده از این معادلات، مدلهای ریاضی کاملا انتزاعی را به پیشبینیهای واقعی جهان، ربط میدهیم. این معادلات، در مطالب بالا نوشته شد:
سمت چپ معادله، یعنی به طور کامل در مورد هندسه فضا-زمان صحبت میکند. این قسمت از تانسور ریچی، تانسور متریک و کمیت نردهای ریچی، تشکیل شده است. در مقابل، سمت راست معادله، یعنی ، در مورد آنچه در کیهان وجود دارد صحبت میکند. در این قسمت تانسور تکانه-انرژی در کسری متشکل از ثابتهای مختلف ضرب شده است. کسر نوشته شده در معادله بالا، تعیینکننده شدت گرانش در جهان است. کسر به سرعت نور و ثابت جهانی گرانش وابسته است. سوالی که ممکن است مطرح شود آن است که چرا نوشتن این کسر در معادلات میدان اینشتین بسیار مهم است. کسر سازگاری نسبیت با بقیه نظریههای فیزیکی را تضمین میکند. همچنین، اگر نیروی جاذبه بسیار ضعیف باشد، از معادلات میدان اینشتین به معادلات نیوتن میرسیم.
توجه به این نکته مهم است که حل معادلات میدان اینشتین بسیار سخت است. همانطور که در معادلات بالا دیدیم، تانسور ریچی و کمیت نردهای ریچی از محاسبات بسیار پیچیدهای شامل مشتق، جمع و حاصلضرب تانسورهای متریک تشکیل شدهاند. همچنین، دو سمت معادله به یکدیگر ربط دارند. آنچه در جهان وجود دارد به فضا-زمان میگوید چگونه و تا چه اندازه انحنا داشته باشد. متقابلا، انحنای فضا-زمان در مورد چگونگی حرکت اجسام صحبت میکند.
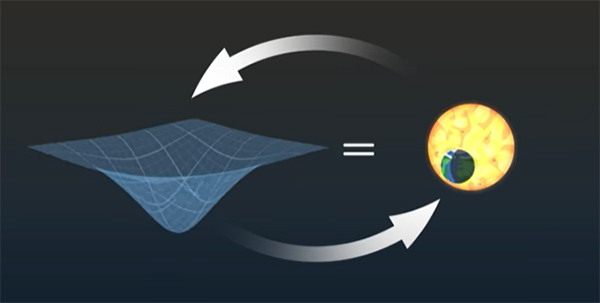
حل معادلات میدانی اینشتین روی کاغذ بسیار سخت و تقریبا غیرممکن است. در این حالت از تقریب و شبیهسازیهای پیشرفته کامپیوتری استفاده میشود. همانطور که در مطالب بالا گفتیم، انحنای فضا-زمان توسط تانسور ریچی و کمیت نردهای ریچی در معادلات میدان اینشتین، بیان میشوند. در جهان چهاربعدی که ما در آن زندگی میکنیم، تقارن بسیار جالبی در این معادلات وجود دارند. اگر در معادلات میدان اینشتین جای تانسور ریچی و تانسور تکانه-انرژی را عوض و کسر را برعکس کنیم، معادله همچنان معتبر خواهد بود. معادله جدید بهدست آمده به طور کامل معادل است و در برخی حالتها استفاده از آن بسیار سادهتر خواهد بود.
در ادامه، در مورد چرایی عوض کردن تانسورهای ریچی و تکانه -زمان و معتبر ماندن معادلات میدان اینشتین صحبت خواهیم کرد.
گرچه معادلات اینشتین بسیار پیچیده هستند، اما در برخی حالتها، راهحلهای دقیقی برای آن وجود دارند. فضایی تهی از ماده و خلأ را در نظر بگیرید که جرمی به جرم M در آن قرار داده میشود. برای جرم M، فرضهای زیر را انجام میدهیم:
- جرم M به طور کامل کروی است.
- پایدار است و با گذر زمان تغییر نمیکند.
- هیچ ویژگی الکتریکی یا مغناطیسی ندارد.
این جسم ممکن است ستارهای مانند خورشید یا سیارهای مانند زمین باشد. هدف ما آن است که تانسور متریک و در نتیجه هندسه فضا-زمان را در نقطهای خارج از جسم بهدست آوریم. در ابتدا، دستگاه مختصاتی را انتخاب و نقطه موردنظر را از فاصله بسیار دور تماشا میکنیم. همچنین، زمان را روی ساعت خود، t، اندازه میگیریم. فاصله بین مرکز جسم و نقطه خارج از آن برابر r است و با دو زاویه و مشخص میشود.
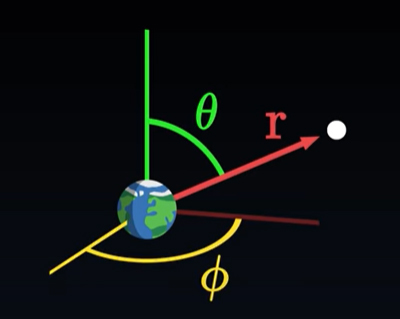
گفتیم نقطه موردنظر خارج از جرم M و در خلأ قرار گرفته است، بنابراین تانسور انرژی-تکانه آن برابر صفر خواهد بود.
از صورت دوم معادلات میدانی اینشتین، یعنی ، استفاده میکنیم و مقدار را برابر صفر قرار میدهیم:
با توجه به رابطه بالا به این نتیجه میرسیم که مقدار تانسور ریچی نیز برابر صفر خواهد بود:
برای بهدست آوردن تانسور متریک با استفاده از تانسور ریچی باید محاسبات کسلکننده بسیاری انجام دهیم و معادلات دیفرانسیلی متعددی را حل کنیم. اما باید از تقارنی که به مسئله دادیم تشکر کنیم. بهدست آوردن حل دقیق، هنوز ممکن است.

متریک شوارتزشیلد به جرم جسم بستگی دارد. اگر جرم جسم برابر صفر باشد به متریک مینکوفسکی میرسیم. این متریک، فضا-زمان تهی را توصیف میکند.
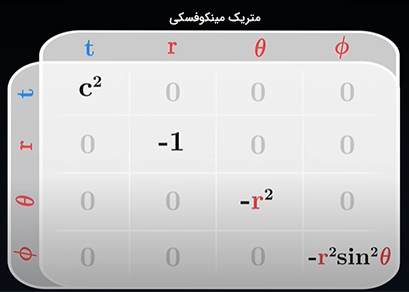
در اطراف جسمی مانند زمین، متریک شوارتزشیلد نشان میدهد، فضا-زمان خمیده شده، انحنا دارد و هرچه به زمین نزدیکتر میشویم، مقدار انحنا بیشتر خواهد شد. اگر سیارهای را در نظر بگیریم، سطح آن به ما اجازه نمیدهد که خیلی به مرکز نزدیک شویم. متریک شوارتزشیلد داخل سیاره معتبر نیست. اکنون جسم بسیار فشردهای را در نظر بگیرید که در آن سطح به مرکز بسیار نزدیک است. در این حالت، تا جایی میتوانیم نزدیک شویم که قسمت زمانی متریک با مختصات انتخاب شده در بالا، برابر صفر شود. به نقطهای بدون بازگشت رسیدهایم. زمان نسبت به بیرون تا بینهایت کش آمده است. به بیان دیگر، زمان در این نقطه، نسبت به محیط بیرون بسیار کند میگذرد. به این فاصله، شعاع شوارتزشیلد یا افق رویداد سیاهچاله گفته میشود:
جمعبندی و کاربردها
تاکنون در مورد ریاضیات حاکم بر نسبیت عام و معادلات میدان اینشتین صحبت کردیم. در این بخش، در مورد گامهای لازم برای حل مسئله در نسبیت عام صحبت میکنیم.
گام اول
در ابتدا، هندسه فضا-زمان را برای حل مسئله تعیین میکنیم. این بدان معنا است که متریک موردنظر باید انتخاب شود. در فضای تهی از متریک مینکوفسکی، استفاده میکنیم. فضا-زمان در خلأ تخت و نسبیت حاکم، نسبیت خاص اینشتین است. اگر جسمی کروی و پایدار در فضا وجود داشته باشد از متریک شوارتزشیلد استفاده میکنیم. این متریک یکی از پرکاربردترین متریکها است، زیرا علاوه بر سادگی، برای شبیهسازی بسیاری از حالتها میتوان از آن استفاده کرد. از این متریک میتوان برای توصیف سیاره، ستاره و حتی سیاهچاله ایستا استفاده کرد. متریکهای عجیبوغریب دیگری، مانند متریک FLRW، نیز وجود دارند. متریک FLWR، جهان همگن را توصیف میکند. متریک دیگری به نام متریک Kerr برای توصیف سیاهچاله چرخان استفاده میشود.

گام دوم
پس از مشخص کردن متریک موردنظر، مختصاتهای مناسب را انتخاب میکنیم. اینکه در چه حالتی قرار داشته باشیم، برخی از مختصاتها مناسبتر از مختصاتهای دیگر هستند. مختصات رایج انتخاب شده برای متریک مینکوفسکی، مختصات دکارتی است. ساختار این مختصات، خطی است. مختصات مناسب برای متریک شوارتزشیلد، مختصات کروی است. این مختصات، تقارن جرم مرکزی را نشان میدهد. اما نکته مهمی در اینجا وجود دارد. شاید مسئلهای که باید حل کنیم مطابق هیچیک از راهحلهای ارائه شده برای معادلات میدان اینشتین نباشد. در این حالت، باید مناسبترین مختصات را با توجه به مسئله داده شده انتخاب کنیم. برای انجام این کار، به طور مستقیم از معادلات میدان اینشتین شروع میکنیم و شکلهای مختلف تانسور انحنا را برای پیدا کردن تانسور متریک مناسب بهدست میآوریم. این فرایند بسیار سخت است و برای رسیدن به متریک مناسب باید از تقریبهای مناسب و شبیهسازیهای پیشرفته استفاده کرد.
گام سوم
تا اینجا، هندسه فضا-زمان و مختصات مناسب را برای حل مسئله انتخاب کردهایم. در ادامه، تقارنهای مسئله را برای کاهش ابعاد، تحلیل و بررسی میکنیم. به عنوان مثال، برای توصیف سیبی که به صورت عمودی به سمت زمین سقوط میکند، تنها به فضای یکبعدی در امتداد یک محور مختصات، نیاز داریم. به طور مشابه، مسیر حرکت جسمی چرخان به دور جرمی کروی، به دلیل تقارن، داخل صفحه قرار گرفته است. جسم چرخان هیچ دلیلی برای خروج از صفحه و حرکت به سمت بالا یا پایین ندارد. در این حالت، مختصات را میتوان به گونهای انتخاب کرد که داخل صفحه فرضی قرار داشته باشد. بنابراین، ابعاد مسئله به دو کاهش مییابد.
گام چهارم
پس از انتخاب متریک مناسب و استفاده از تقارنهای مسئله، راهحل مناسب را جستجو میکنیم. دو حالت برای حل مسئله وجود دارند.
حالت اول
به دنبال یافتن مولفههای سرعت حرکت جسم در فضا-زمان هستیم. به عنوان مثال، شاید بخواهیم مولفه زمانی را بهدست بیاوریم مولفه زمانی نشان میدهد زمان ما با چه نرخی نسبت به زمان ویژه میگذرد. در اینجا از این حقیقت استفاده میکنیم که تمام اجسام در جهان با سرعت نور حرکت میکنند. اندازه بردار سرعت همواره باید برابر c (سرعت نور) باشد. در این حالت، به معادلهای میرسیم که مولفههای سرعت را به یکدیگر ربط میدهد.
حالت دوم
شاید بخواهیم تغییرات مولفههای سرعت را نسبت به زمان بدانیم. به بیان دیگر، در مورد چگونگی شتاب گرفتن جسم در مختصات انتخاب شده صحبت میکنیم. در این حالت، کل مسیر حرکت جسم در فضا-زمان را توصیف خواهیم کرد. به عنوان مثال، شاید بخواهیم حرکت سیبی که به سمت زمین سقوط میکند یا حرکت زمین به دور خورشید را توصیف کنیم. در این حالت، باید نمادهای کریستوفل را بهدست آوریم. با دانستن نمادهای کریستوفل، به راحتی از معادله ژئودزیک استفاده میکنیم. به عنوان مثال، در حالتی که سیب از درخت به سمت زمین سقوط میکند، معادله ژئودزیک به ما میگوید ارتفاع سیب با شیب منفی کم میشود.
با طی کردن گامهای گفته شده، مسئلههای زیادی را میتوان در فیزیک حل کرد. در ادامه، برای درک بهتر این موضوع، چند مثال را با یکدیگر بررسی میکنیم.
مثال اتساع زمان
فرض کنید فضانوردی در ایستگاه فضایی قرار دارد. در این قسمت، اتساع زمانی فضانورد را محاسبه میکنیم. برای حل این مثال، گامهای گفته شده در قسمت بالا را تک به تک طی میکنیم.
در ابتدا، متریکی مناسب مسئله داده شده انتخاب میکنیم. فضانورد در ایستگاه فضایی به دور زمین میچرخد. زمین را کروی در نظر میگیریم و از چرخش آن به دور خود صرفنظر میکنیم، زیرا سرعت چرخش زمین به دور خود، نسبت به سرعت نور بسیار کوچکتر است. در این چارچوب ساده شده، فضا-زمان بیرون از زمین میتواند توسط متریک شوارتزشیلد، مدلسازی شود. متریک شوارتزشیلد را میتوانیم برحسب مختصات کروی بیان کنیم. به هنگام حل این مثال فرض میکنیم که در فاصله بسیار دوری نسبت به زمین قرار گرفتهایم. همچنین، زمان اندازهگیری شده نسبت به ساعت ما، با t بیان میشود. مختصات ماهواره در تصویر زیر نشان داده شده است.
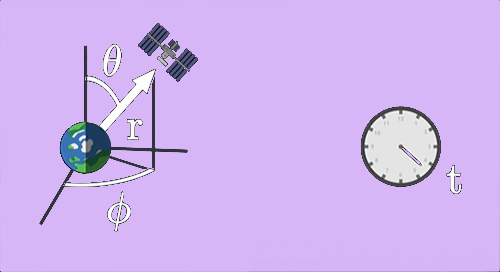
تانسور متریک به شکل زیر خواهد بود:

تا اینجا، تانسور متریک را میدانیم. در ادامه، با استفاده از تقارنهای موجود در مسئله میتوانیم تعداد مولفههای تانسور متریک را کاهش دهیم. برای سادگی فرض میکنیم ایستگاه فضایی در مداری دایرهای به دور زمین میچرخد. در مطالب بالا گفتیم، در چرخش جسمی به دور سیاره یا خورشید، مدار حرکت جسم در صفحهای دوبعدی قرار میگیرد. بنابراین، به زاویه و همچنین، به r نیازی نداریم، زیرا در مدار دایرهای ثابت باقی میماند. بنابراین، ستونها و سطرهای مربوط به r و در تانسور متریک داده شده حذف میشوند.
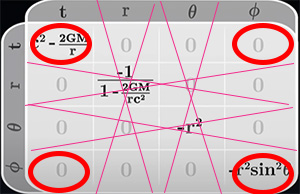
موقعیت فضانورد در ایستگاه فضایی تنها با استفاده از دو کمیت، توصیف میشود:
- زمان t
- زاویه
پس از تعین ماتریس متریک، میتوانیم مسئله را حل کنیم. زمان اتساع به صورت نسبت نرخ گذر زمان ما به نرخ گذر زمان ویژه فضانورد، تعریف میشود. به بیان دیگر، این نسبت برابر مولفه زمانی سرعت است. برای تعیین مولفه زمانی سرعت، ، از اندازه سرعت استفاده میکنیم. تمام اجسام در فضا-زمان با سرعت نور حرکت میکنند. فضانورد هم در فضا و هم در زمان حرکت میکند، اما سرعت کلی آن در فضا-زمان، هموراه برابر c است. اندازه بردار سرعت در نسبیت عام با استفاده از تانسور متریک بهدست میآید.
رابطه فوق، حالت کلیتر و تعمیم یافته قضیه فیثاغورث است. از آنجا که مختصات فضانورد دوبعدی است، و برابر t و هستند. بنابراین، رابطه فوق به صورت زیر نوشته میشود:
در حل این مثال از ماتریس شوارتزشیلد استفاده میشود:
| t | ||
| 0 | t | |
| 0 |
با استفاده از این ماتریس و قرار دادن مولفههای آن در رابطه بالا، به رابطه زیر میرسیم:
دو مولفه سرعت به طور مستقیم توسط رابطه بالا به یکدیگر مربوط شدهاند. از یک سو، سرعت زاویهای یا را داریم. سرعت زاویهای نرخ افزایش زاویه فضانورد به هنگام چرخش به دور زمین را نشان میدهد. در سوی دیگر، سرعت زمانی یا را داریم. هدف ما محاسبه این مولفه است. رابطه بالا را بر حسب مولفه زمانی سرعت مرتب میکنیم:
از فیزیک کلاسیک میدانیم سرعت مداری فضانورد به هنگام چرخش به دور زمین و سرعت زاویهای با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
این سرعت را در رابطه قرار میدهیم:
سرانجام به رابطهای برای محاسبه اتساع زمان یا تاخیر زمانی فضانورد نسبت به ناظری در دوردست رسیدیم. اتساع زمانی را میتوانیم برای ایستگاه بینالمللی فضایی و با استفاده از دادههای زیر بهدست اوریم:
با قرار دادن دادههای فوق در رابطه ، تاخیر زمانی در ایستگاه فضایی برابر یک نانو ثانیه به ازای هر ثانیه زمان ویژه بهدست میآید. به بیان دیگر، زمان برای فضانورد نسبت به ناظر دوردست کندتر میگذرد.
مثال سقوط آزاد
در این مثال، سقوط ماهواره به روی خورشید را توصیف میکنیم. در اینجا فرض میکنیم ماهواره به صورت عمودی سقوط میکند. همچنین، خورشید را کروی و پایدار در نظر میگیریم. از اینرو، متریک مناسب برای این مثال، متریک شوارتزشیلد خواهد بود. همانند مثال قبل، از مختصات کروی برای حل این مسئله استفاده میکنیم. همچنین، ماهواره و خورشید در فاصله بسیار دوری نسبت به ناظر قرار گرفتهاند. زمان اندازهگیری شده با ساعت ناظر را با t نشان میدهیم. سیستم ماهواره و خورشید در تصویر زیر نشان داده شده است.
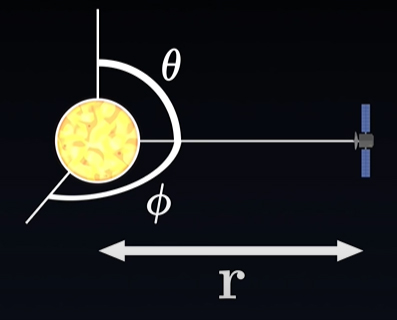
از آنجا که ماهواره به صورت عمودی به سمت خورشید سقوط میکند، زاویههای و تغییر نمیکنند و میتوانیم از آنها صرفنظر کنیم. بنابراین، مکان ماهواره تنها به ارتفاع آن از سطح خورشید و زمان، بستگی دارد. تانسور شوارتزشیلد در این حالت به صورت زیر نوشته میشود:
| r | t | |
| 0 | t | |
| 0 | r |
در این مثال، محاسبه سرعت حرکت ماهواره هدف اصلی نیست، بلکه به دنبال بهدست آوردن شتاب مختصات آن هستیم. برای انجام این کار باید نمادهای کریستوفل را محاسبه کنیم. در متریک شوارتزشیلد با مختصات داده شده، نمادهای کریستوفل به صورت زیر بهدست میآیند:
نمادهای کریستوفل بهدست آمده را در معادله ژئودزیک قرار میدهیم.
پس از قرار دادن نمادهای کریستوفل در معادله ژئودزیک، به دو معادله بالا میرسیم. برطبق این معادلات، شتاب هر مختصات، حرکت ماهواره را توصیف میکند. یک معادله مربوط به شتاب زمانی و معادله دیگر مربوط به شتاب ارتفاع ماهواره است. با استفاده از این دو معادله میتوانیم مسیر حرکت ماهواره را نسبت به زمان ویژه بهدست آوریم. اگر سرعت اولیه ماهواره را بدانیم، شتاب آن را میتوانیم محاسبه کنیم. دو معادله بهدست آمده را با دقت بیشتری میتوان بررسی کرد.
ابتدا معادله زیر را در نظر میگیریم:
پس از مرتبسازی، معادله فوق به صورت زیر نوشته میشود:
معادله بالا، پایستگی کمیت مشخصی را نشان میدهد. این کمیت متناسب با انرژی است. انرژی در متریک شوارتزشیلد به ارتفاع و حرکت آن در زمان بستگی دارد.
مثال اشعه نور
در این مثال، مسیر نور در نزدیکی سیاهچاله را بررسی میکنیم. اگر سیاهچاله ایستا باشد، فضا-زمان با استفاده از متریک شوارتزشیلد توصیف میشود. نور در نسبیت عام بسیار مهم و ویژه است، بنابراین باید رفتار متفاوتی با آن داشته باشیم. چرا؟ برای پاسخ به این پرسش باید به کمیتهای بنیادی دقت کنیم.
در قسمتهای قبل دیدیم هر جسم دلخواهی، خط جهانی را در فضا-زمان دنبال میکند. این خط جهانی میتواند به قسمتهای مساوی تقسیم شود. این فاصلههای موازی در امتداد منحنی به ما اجازه میدهند آن را به شکل حرکت تفسیر کنیم. تعریف زمان ویژه از اینجا میآید. با گذشت زمان ویژه، جسم در فضا-زمان حرکت میکند. در اینجا، بردار سرعت فضا-زمان را تعریف میکنیم. اما نور همانند جسم مادی نیست و هیچ مسافتی را در فضا-زمان طی نمیکند. فاصله دو نقطه در امتداد خط جهانی نور، همواره برابر صفر خواهد بود. بنابراین، تعریف زمان ویژه برای نور بیمعنا است. هنگامی که با نور برخورد میکنیم، باید بسیار بادقت عمل کنیم. زیرا امکان تعریف بردار سرعت ویژه برای نور وجود ندارد.
برای حل این مسئله باید از تقسیمبندی جدیدی استفاده کنیم. به این تقسیمبندی جدید، «پارامتر آفین» (Affine Parameter) گفته میشود. برخلاف زمان ویژه، پارامتر آفین هیچ معنای فیزیکی ندارد. این پارامتر هیچ فاصلهای را در فضا-زمان اندازه نمیگیرد. این پارامتر، تنها تقسیمبندی دلخواه و ابزاری ریاضی برای استفاده در معادلات است. با استفاده از این پارامتر میتوانیم بردار سرعتی به صورت ، تعریف و از معادله ژئودزیک استفاده کنیم.
توجه به این نکته مهم است که از اندازه بردار نیز میتوانیم استفاده کنیم. سرعت ساختگی است و از آن تنها برای نور استفاده میشود. نٔرم این بردار برابر صفر است، زیرا نور هیچ مسافتی را طی نمیکند.
گرچه نور به طور کامل با جسم مادی تفاوت دارد، اما هنوز میتوانیم از تحلیلهای مثالهای قبلی استفاده کنیم. بنابراین، معادلههای ژئودزیک حاکم بر مسیر حرکت نور در امتداد پارامتر آفین به دور سیاهچاله را میتوانیم بهدست آوریم:
این معادلات به ما میگویند مسیر نور، هنگام نزدیک شدن به سیاهچاله، منحرف میشود. این حالت، شبیه همگرایی گرانشی است.

اصل هم ارزی و معادلات میدان اینشتین
گسترش معادلات میدان اینشتین در حدود ده سال زمان برد. اینشتین در آن زمان به ریاضیدانهای بسیار بزرگی دسترسی داشت. در مطالب بالا گفتیم اگر در معادلات اینشتین، جای تانسورهای R و T را با یکدیگر عوض و کسر نشاندهنده شدت گرانش را برعکس کنیم، معادله بهدست آمده به طور کامل، معادل معادله قبل از تعویض تانسورها و برعکس کردن کسر خواهد بود. اما چرا؟ در ادامه و برای پاسخ به این پرسش، باید با اصل همارزی آشنا باشیم.
اصل هم ارزی چیست ؟
فرض کنید در جعبهای بدون هیچ پنجرهای قرار داریم. دو حالت زیر را در نظر بگیرید:
- جعبه در فضا قرار دارد و با شتاب g، شتاب جاذبه گرانشی زمین، حرکت میکند.
- جعبه روی زمین قرار دارد و تحت شتاب جاذبه گرانشی زمین قرار دارد.
سوالی که ممکن است مطرح شود آن است که آیا میتوانید تشخیص دهید روی زمین قرار دارید یا در فضا حرکت میکنید. پاسخ به این پرسش، خیر است. در واقع، هیچ آزمایشی برای تمیز دادن این دو حالت از یکدیگر وجود ندارد. اما نمیتوانیم با قطعیت بگوییم این موضوع کاملا برقرار است. اگر جعبه در فضا قرار داشته باشد و با شتاب g حرکت کند، تمام قسمتهای جعبه و حتی شما با شتاب g حرکت خواهید کرد. در مقابل، اگر جعبه روی سطح زمین قرار داشته باشد و با توجه به آنکه مقدار g با تغییر ارتفاع از سطح زمین تغییر میکند، مقدار g در کف جعبه با مقدار آن در بالای جعبه، تفاوت بسیار اندکی خواهد داشت. اگر بتوانیم این تفاوت بسیار کوچک را اندازه بگیریم، متوجه تفاوت دو موقعیت میشویم. اینشتین، نام این موقعیت را اصل همارزی گذاشت.
اینشتین اصل دیگری را نیز بیان کرد: نور در میدان گرانشی، خمیده میشود. به بیان دیگر، میدان گرانشی مسیر حرکت نور را تغییر میدهد. فرض کنید همانند حالت نخست در جعبهای قرار دارید و جعبه با شتاب g حرکت میکند. چراغقوهای را روشن و نور آن را به دیوار روبرو بتابانید. نور از چراغقوه خارج و به دیوار روبرو میتابد. به این نکته توجه داشته باشید که نور پس از طی مدت زمان بسیار کوتاهی به دیوار روبرو میرسد. جعبه با شتاب g به سمت بالا حرکت میکند. هنگامی که نور نصف مسیر بین دو دیوار را طی میکند، جعبه با شتاب g کمی به سمت بالا رفته است. بنابراین هنگامی که نور در نصف مسیر قرار دارد، ارتفاع جعبه کمی افزایش مییابد. هنگامی که نور به دیوار روبرو میرسد، ارتفاع جعبه باز هم افزایش یافته است. بنابراین، در حالت کلی اینگونه به نظر میرسد که نور به هنگام رسیدن به دیوار روبرو، به سمت پایین خم شده و به کف جعبه رسیده است.
بر طبق اصل همارزی اینشتین، حالتهای یک و دو قابل تشخیص از یکدیگر نیستند و ناظر داخل جعبه متوجه تفاوت دو موقعیت نخواهد شد. از اینرو، اگر جعبه روی زمین و در میدان گرانشی آن قرار داشته باشد، نور چراغقوه باید خمیده شود. به بیان دیگر، نور باید در حضور میدان گرانشی زمین خم شود. خمیدگی نور در حضور میدان گرانشی به اثبات رسیده است.
بر طبق نظریه فیزیک کلاسیک، نیروی گرانشی بین دو جسم به جرمهای m و M که در فاصله r از یکدیگر قرار دارند، به صورت زیر نوشته میشود:
در رابطه بالا، G ثابت جهانی گرانش است. آیا این رابطه برای نور صدق میکند؟ خیر، زیرا نور از بستههای انرژی به نام فوتون تشکیل شده است. فوتونهای بدون جرم هستند. بنابراین، بر طبق این رابطه انتظار میرود نور به مسیر حرکت خود روی خط راست ادامه دهد و در میدان گرانشی خم نشود. بنابراین، این رابطه برای نور کاربردی ندارد. اینشتین برای حل این مشکل، فضا-زمان خمیده را مطرح کرد. فضا-زمان در حضور جسمی با جرم مشخص، خمیده میشود. بنابراین، نور در نزدیکی خورشید یا هر جسم کلانجرمی، به جای حرکت در فضا-زمان مسطح، در فضا-زمان خمیده حرکت میکند. شاید از خود بپرسید چرا اینشتین خمیدگی فضا-زمان را مطرح کرد. در ادامه به این پرسش پاسخ میدهیم.
چرا فضا-زمان در حضور جرم M خمیده می شود ؟
در حالت کلی، فضا از سه بعد x و y و z تشکیل شده است. اگر زمان را به آنها اضافه کنیم، فضا-زمان چهاربعدی خواهیم داشت. رسم چهار بعد برای ما که تنها تا سه بعد را میشناسیم، بسیار سخت است، بنابراین فضا را روی محور عمودی و زمان را روی محور افقی یا برعکس، نشان میدهیم. سرعت ثابت در فضا-زمان با خطی با شیب ثابت نشان داده میشود. اگر حرکت شتابدار باشد، نمودار خط راست نیست و منحنی با انحنای مشخص خواهد بود. معنای شتاب آن است که هرچه زمان طولانیتر باشد، جسم بیشتر جلو میرود. بنابراین، نمودار شتاب انحنا دارد. از آنجا که گرانش سبب ایجاد شتاب میشود، نموداری با انحنای مشخص در مختصات فضا-زمان، ایجاد میکند.
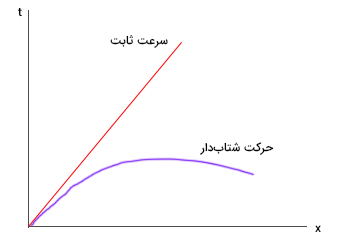
تعداد معادلات میدان اینشتین چند تا است ؟
در نگاه نخست اینگونه به نظر میرسد که تعداد معادلات اینشتین، ۱۶ معادله است. اما ۶ تا از معادلات، تکرار میشوند. بنابراین، تعداد معادلهها به ده معادله کاهش مییابد. در مطالب بالا گفتیم، معادلات میدان اینشتین به شکل زیر نوشته میشوند:
اندیسهای و بین صفر تا ۳ تغییر میکنند. بنابراین، در حالت کلی، تعداد این معادلات برابر ۱۶ به نظر میرسد، اما شش تا از این معادلات تکراری هستند. بنابراین، تعداد کل معادلات میدان اینشتین برابر ۱۰ است.
در مطالب بالا در مورد هر یک از کمیتهای استفاده شده در معادلات میدان اینشتین توضیح دادیم. همچنین، گفتیم این معادلات با استفاده از برخی شبیهسازیها و تقریبهای فرض شده برای حالتهای خاص، حل شدهاند. در ادامه، به چند مورد از تلاشهای انجام شده برای حل معادلات میدان اینشتین اشاره میکنیم.
حل معادلات میدان اینشتین
یکی از راههای حل کردن معادلات میدان اینشتین درنظر گرفتن سیستمی با تقارن بسیار زیاد است. در مطالب بالا در مورد متریک شوارتزشیلد، صحبت کردیم. با استفاده از این متریک، حل معادلات میدان اینشتین بسیار راحتتر خواهد بود.
متریک شوارتزشیلد، ایستا است، با زمان تغییر نمیکند و تقارن کروی دارد. این سه فرضیه به ما میگوید تانسور متریک، تنها مولفههای قطری دارد و مابقی مولفههای آن برابر صفر هستند. همچنین، بهترین مختصات برای این متریک، مختصات کروی است. بنابراین، با استفاده از مختصات ، تانسور متریک به صورت زیر نوشته میشود:
محاسبه دو مولفه اول قطری تانسور g خیلی سخت نیست، ولی نیازمند محاسبات طولانی و حوصلهسربر است. پس از انجام این محاسبات، دو مولفه مجهول بهدست میآیند و ماتریس متریک به صورت زیر نوشته میشود:
به این حل، حل شوارتزشیلد گفته میشود. حلهای دیگری نیز برای معادلات میدان اینشتین ارائه شدهاند. به بیان دیگر، روشهای مختلفی برای حل این معادلات پیشنهاد و استفاده شدهاند. فیزیکدانی به نام «هنس استفانی» (Hans Stephani) و همکارانش، کتابی را در این زمینه به نام «حلهای دقیق معادلات میدانی اینشتین» (Exact Solutions of Einstein's Field Equations) نوشتهاند. در این کتاب، روشهای متعددی برای حل این معادلات پیشنهاد و با جزییات کامل در مورد آنها توضیح داده شده است.

گروههای پژوهشی زیادی از نخستین سالهای پس از مطرح کردن معادلات میدان اینشتین، به دنبال راهحلهای مختلف برای حل دقیق این معادلات بودند. نتیجه پژوهش آنها در مجلههای معتبر بینالمللی چاپ شدهاند. برخی از این مقالهها در ادامه آورده شدهاند:
- مقاله «حلهای ایستای معادلات میدان اینشتین برای کرههای سیال» (Static Solutions of Einsteins's Field Equations for Spheres of Fluid): این مقاله توسط فیزیکدانی به نام «ریچارد تالمن» (Richard C. Tolman) در سال ۱۹۳۹ میلادی در مجله Physical Reviews به چاپ رسید.
- مقاله «گروهی از حلهایِ دقیق معادلات میدان اینشتین» (A Class of Exact Solutions of Einsteins's Field Equations): این مقاله توسط فیزیکدانی به نام «سودهانسو داتا ماجومدار» (Sudhansu Datta Majumdar) در سال ۱۹۴۷ میلادی در مجله Physical Reviews به چاپ رسید.
مقالههای بسیار دیگری در این زمینه به چاپ رسیدهاند. در برخی از آنها از شبیهسازیهای کامپیوتری برای حل این معادلات استفاده شده است.
تا اینجا، با معادلات میدان اینشتین آشنا شدیم و در مورد کمیتهای استفاده شده در این معادلات صحبت کردیم. یکی از این کمیتها، ، ثابت کیهانی است. اینشتین ابتدا خود را برای استفاده این کمیت در معادلات میدان، سرزنش کرد. اما بعد مشخص شد وجود کمیت ثابت کیهانی در معادلات میدان، صحیح است. در ادامه، در مورد ثابت کیهانی با جزییات بیشتری صحبت خواهیم کرد.
ثابت کیهانی: بزرگ ترین اشتباه اینشتین
معادلات میدان اینشتین در سال ۱۹۱۵ میلادی توسط او به جامعه علمی معرفی شدند. در معادله معروف اینشتین، یعنی ، تنها جرم و انرژی به یکدیگر مربوط میشوند. اما در معادلات میدان، جرم، انرژی و گرانش به یکدیگر ربط داده شدهاند. این معادلات، جایگزین رابطه نیوتن برای نیروی گرانش هستند. همانطور که قانون دوم نیوتن، رابطه بین شتاب و نیرو را بیان میکند، معادلات میدانی اینشتین رابطه بین جرم و انرژی و خمیدگی فضا-زمان را توضیح میدهند. این معادلات نتیجه مشاهدات پدیدههای فیزیکی همراه با ریاضیات پیچیده است.
پس از آنکه مشخص شد معادلات میدان اینشتین به خوبی با معادله نیوتن برای نیروهای ضعیف گرانش تطابق دارند و شکل غیرمعمول مدار سیاره تیر را به خوبی توضیح میدهند، اینشتین به دنبال آن بود که با استفاده از این معادلات کیهان را به صورت کلی توصیف کند. به این نکته توجه داشته باشید که کیهان و هر آنچه در آن وجود دارد به اندازهای پیچیده هستند که توصیف آن، تنها توسط چند معادله، غیرممکن به نظر میرسد. اما اگر کیهان را از فاصله دور نگاه کنیم، با تقریب خوبی میتوانیم چگالی آن را در همه جا و در همه جهتها، یکسان در نظر بگیریم. اینشتین با این فرض توانست معادلات میدان را حل کند. در واقع، با فرض ثابت بودن چگالی کیهان در همه جا، تعداد معادلات میدان از دو معادله پیچیده به دو معادله کاهش یافت. اینشتین پس از حل دو معادله، به دو نتیجه رسید:
- چگالی کیهان متناسب با انحنای کیهان است. به بیان دیگر، هر چه مقدار ماده موجود در کیهان بیشتر باشد، انحنای آن نیز بیشتر خواهد بود.
- چگالی باید صفر باشد. چگالی صفر بدان معنا است که هیچ مادهای نمیتواند در کیهان وجود داشته باشد.
چگالی صفر، مشکلی بود که ظاهر شد و باید راهی برای رفع آن پیدا میشد. دو راهحل برای رفع این مشکل پیشنهاد شد.
- راهحلی که توسط اینشتین پیشنهاد شد.
- راهحلی که توسط او پیشنهاد نشد.
اینشتین با بررسی معادلات خود به این نتیجه رسید که با اضافه کردن عبارتی بسیار ساده به معادلات، میتواند این مشکل را حل کند. اضافه کردن این عبارت، هیچ یک از قوانین بنیادی فیزیک را نقض نمیکرد. عبارت اضافه شده به معادلات میدان اینشتین، ثابت کیهانی ()، نامیده شد. در این حالت، مقدار چگالی کیهان صفر بهدست نمیآید، بلکه متناسب با است. بنابراین، اگر عبارت اضافه شده غیرصفر باشد، ماده در کیهان وجود دارد.
راهحل دوم، فرض اینشتین از کیهان را زیر سوال برد. اینشتین، کیهان را ایستا و بدون تغییر در نظر گرفته بود. فرضیه کلی او در مورد کیهان آن بود که ایستا است و منقبض یا منبسط نمیشود. اینشتین هنگام بهدست آوردن معادلات میدان خود، اشتباه کوچکی مرتکب شد (). با انجام این اشتباه، امکان هرگونه تغییری در کیهان، مانند انبساط یا انقباض، از بین رفت. راهحل دوم وجود داشت، ولی اینشتین آن را ندید. راهحل دوم توسط فیزیکدانی به نام «الکساندر فریدمن» (Alexander Friedmann) ارائه شد. عبارت استفاده شده توسط فریدمن، مشابه عبارت استفاده شده توسط اینشتین بود، با این تفاوت که فریدمن کیهان را متغیر فرض کرد.

در راهحل دوم نیز تعداد معادلات میدان اینشتین به دو معادله کاهش یافتند. معادله اول تغییرات چگالی کیهان را با تغییرات اندازه آن، توصیف میکند. بر طبق این معادله، هر چه کیهان بزرگتر شود، چگالی آن کمتر خواهد شد.
بر طبق معادله دوم بهدست آمده توسط فریدمن، کاهش شتاب کیهان متناسب با تفاضل چگالی و ثابت اینشتین است. به بیان دیگر، ماده موجود در کیهان، خود را از نظر گرانشی جذب میکند. بنابراین، کیهان تمایل دارد به سمت داخل کشیده شود و نرخ انقباض یا انبساط را کاهش دهد، مگر آنکه ثابت اینشتین واقعی باشد یا مقدار آن به اندازهای بزرگ باشد که بر نیروی جاذبه گرانشی غلبه کند. بنابراین، این راهحلی بود که از دید اینشتین دور ماند. سالها بعد و با مشاهدههای ستارهشناسان، مشخص شد که کیهان در حال انبساط است. بنابراین، هیچ عبارت دیگری نیازی نبود به معادلات میدان اینشتین اضافه شود.
ده سال پس از مرگ اینشتین، دانشمندان به این نتیجه رسیدند که نرخ انبساط کیهان ثابت نیست و کاهش نمییابد، بلکه جهان با نرخ افزایشی در حال منبسط شدن است. در نتیجه، مشخص شد ثابت اینشتین یا ثابت کیهانی در توصیف جهان، نقش دارد. اما، کیهان تصور شده توسط اینشتین با آنچه توسط معادلات بهدست آمد، بسیار متفاوت بود.













در ابتدا با تشکر از توضیحات و حوصله نویسنده در ارایه مطالب و اینکه کار ارزشمندی انجام شده اما نکته ایی که توجه من را به عنوان کسی که با جبر تانسوری آشناست جلب کرد این نکته بود که تصور نویسنده از سطح دانش خواننده یکسان نیست و در طول خواندن مطلب تغییر میکند. یعنی در جایی به تعریف بردار و ماتریس به طوری پرداخته شده که گمان میرود خواننده دانش آموز دبیرستانی باشد یا تازه وارد دانشگاه شده و در جایی دیگر مثل تانسور ریمان و یا توصیف انحنا با کریستوفل ها با داشتن دکتری و تسلط ریاضی نیز کار درک موضوع سخت شده بنابراین فکر میکنم و پیشنهاد میکنم که اصلاح سطح ارایه و تعدیل در پرداختن به هر مطلب انجام گیرد. در کل لذت بردم و مراتب تشکر خود را به نویسنده تقدیم میکنم.
با سلام؛
از ارائه بازخورد شما بسیار سپاسگزاریم. این موارد را حتما در متنهای تخصصی، مجدد بررسی خواهیم کرد.
با تشکر از همراهی شما با مجله فرادرس