تانسور چیست؟ — مفاهیم اصلی

تانسورها در بسیاری از حوزههای علم فیزیک از جمله الاستیسیته، مکانیک سیالات و نسبیت عام، چارچوب ریاضی فشرده و مختصری را برای فرمولبندی و حل مسائل گوناگون فراهم میکنند و به همین دلیل، از اهمیت خاصی برخوردار هستند. از زمینههای دیگری که مفهوم تانسور در آنها کاربرد دارد، میتوان به یادگیری عمیق در علم داده اشاره کرد. در این آموزش، مفاهیم مربوط به تانسور را بیان میکنیم.
تعریف تانسور
«تانسور» (Tensor)، نقطهای از فضا است که توسط یک یا چند شاخص که بیانگر مرتبه آن است، توصیف میشود. بهطور کلی، تانسوری با مرتبه در فضای بعدی، شاخص و مؤلفه دارد و از قواعد تبدیل معینی تبعیت میکند. مثلاً، تانسوری با مرتبه یک در فضای سهبعدی، یک شاخص و 3 مؤلفه دارد. در واقع، تانسورها تعمیمی از اسکالرها (که بدون شاخص هستند)، بردارها (که یک شاخص دارند) و ماتریسها (که دو شاخص دارند) با تعداد دلخواهی از شاخصها هستند.
برای مثال، همانگونه که در شکل زیر میبینید، بردار، ماتریس و تانسور ۶۴ مؤلفه دارند که این مؤلفهها در تانسور بهصورت سهبعدی هستند. از این رو میتوان گفت تانسورها آرایههای چندبعدی دارند.
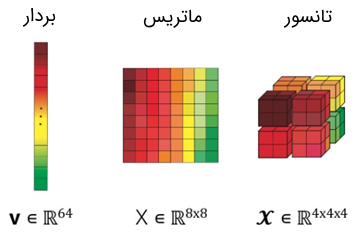
نمادگذاری یک تانسور شبیه ماتریس است (یعنی )، البته تانسور میتواند تعداد دلخواهی از شاخصها را به صورت ، ، و ... داشته باشد. بهطور کلی، تانسوری مثل با مرتبه میتواند یک تانسور از نوع آمیخته باشد (یعنی که (تعداد شاخصهای بالا) را شاخصهای «پادوردا» (Contravariant) و (تعداد شاخصهای پایین) را شاخصهای «هموردا» (Covariant) مینامند. اصطلاحاً گفته میشود تانسور نسبت به شاخصهای بالا پادوردا و نسبت به شاخصهای پایین هموردا است. توجه داشته باشید که محل قرار گرفتن شاخصهای پادوردا و هموردا نیز حائز اهمیت است. برای مثال، و با هم متفاوت هستند.
تانسورهای مرتبه صفر، یک و دو به ترتیب، اسکالر، بردار و ماتریس نامیده میشوند. از این رو، در نمادگذاری تانسوری، برداری مثل را بهصورت () و ماتریس را که تانسوری از نوع است، بهشکل نمایش میدهند.
نمادگذاری تانسوری این امکان را فراهم میکند که اتحادهای برداری و کلیتر را بهطور فشرده و مختصر بنویسیم. برای مثال، ضرب داخلی را میتوان بهصورت تانسوری زیر نوشت:
در اینجا طبق قرارداد جمع انیشتین که بیان میکند هرگاه شاخصی در یک طرف معادله دو بار (یک بار به صورت شاخص بالا و یک بار به صورت شاخص پایین) ظاهر شود، روی آن شاخص جمع زده میشود، روی شاخص جمع میزنیم. مثلاً، در فضای سهبعدی، ضرب داخلی بالا را میتوان اینگونه نوشت:
بهطور مشابه، میتوانیم ضرب خارجی را بهصورت خلاصه زیر بنویسیم:
که تانسور جایگشت نام دارد و به نماد «لوی-چیویتا» (Levi-Civita) معروف است. زمانی که تعداد جایگشتهای سه شاخص ، و زوج و فرد باشد، مقدار این تانسور به ترتیب برابر با و خواهد بود و در صورتی که حداقل دو تا از شاخصهای ، و برابر باشند، مقدار آن صفر خواهد شد. برای مثال، اگر در فضای سهبعدی مؤلفه اول ضرب خارجی را بهدست آوریم، خواهیم داشت:
طبق تعریف، اگر دو شاخص برابر باشند، مقدار تانسور جایگشت صفر میشود، بنابراین در فضای سهبعدی فقط دو حالت داریم:
در جمله اول، جایگشتی نداریم اما در جملهی دوم، ترتیب قرار گرفتن شاخصها متفاوت بوده و بین 2 و 3، یک جایگشت صورت گرفته است. از این رو، مقدار تانسور خواهد بود:
با دستکاری شاخصهای تانسور (بالا و پایین آوردن شاخصها) میتوان عباراتی را که بهشکل تانسور نوشته شدهاند ساده کرد. این کار را میتوان توسط تانسوری بهنام تانسور متریک (، ، و...) انجام داد. بهازای جابهجایی هر شاخص از یک تانسور متریک استفاده میکنیم. برای مثال:
عبارت یک تانسور مرتبه دو است و به فضا و ابعادی بستگی دارد که محاسبات را در آن انجام میدهیم. این تانسور معمولاً بهصورت یک ماتریس قطری است و در این حالت، که وارون است نیز قطری خواهد بود.
جمع و تفریق تانسورها
اگر دو تانسور و هممرتبه بوده و شاخصهای هموردا و پادوردای یکسانی داشته باشند، میتوان آنها را با هم جمع یا از هم کم کرد که حاصل آن نیز تانسوری با همان مرتبه و با همان شاخصها خواهد بود:
لازم به ذکر است که هر دو تانسور و باید در یک فضا و با تعداد ابعاد یکسان تعریف شده باشند.
ادغام و ضرب مستقیم
تعمیم ضرب داخلی تانسورها، «ادغام» (Contraction) تانسور گفته میشود و شامل برابر قرار دادن دو شاخص متفاوت (یکی پادوردا و دیگری هموردا) و جمع بستن روی آن شاخص با استفاده از قرارداد جمع انیشتین است. به بیان دیگر، این کار، تانسور نوع را به یک تانسور نوع تبدیل میکند. مثلاً با ادغام دو شاخص و در تانسور خواهیم داشت:
همانگونه که میبینیم، با ادغام، دو واحد از مرتبه تانسور کم میشود.
اگر دو تانسور در هم ضرب شوند، حاصل، تانسوری خواهد شد که مرتبه آن مساوی با مجموع مرتبههای دو تانسور اولیه است:
در صورتی که یکی از شاخصهای با یکی از شاخصهای برابر باشد، میتوان از ادغام شاخصها استفاده کرد:
چنانچه تمام شاخصهای و با هم برابر باشند، حاصلضرب آنها یک تانسور مرتبه صفر یا بهعبارتی، یک اسکالر خواهد بود.
تقارن و پادتقارن
ترتیب قرار گرفتن تانسورها اهمیت دارد. بهعنوان نمونه، تانسورهای و با هم متفاوت هستند، اما در بعضی موارد این دو تانسور با هم برابرند، یعنی:
در این حالت میگوییم تانسور متقارن است. ولی اگر داشته باشیم:
تانسور پادمتقارن خواهد بود.
مثال
در اینجا برای درک بهتر مفهوم تانسور و نحوه کاربرد آن، تانسوری به نام تانسور الکترومغناطیسی را معرفی میکنیم که در نسبیت عام کاربرد فراوانی دارد. این تانسور یک تانسور مرتبه دو و پادمتقارن است:
که در آن، مشتق جزئی در فضا-زمان مینکوفسکی است و چهاربردار پتانسیل نام دارد که شکل پادوردا و هموردای آن بهترتیب، و هستند. همچنین، پتانسیل برداری، پتانسیل اسکالر و سرعت نور است.
واضح است که این تانسور در فضا-زمان چهاربعدی، مؤلفه دارد و بهشکل یک ماتریس است که عناصر قطر اصلی آن یعنی صفر هستند. برای نمونه، چند مؤلفه این تانسور را در فضای «مینکوفسکی» (Minkowski) بهدست میآوریم:
از آنجایی که است، داریم:
سایر مؤلفهها نیز به همین صورت محاسبه میشوند:
برای بهدست آوردن تانسور پادوردای الکترومغناطیسی، کافی است تانسور پادوردای متریک را در ضرب کنیم:
در فضا-زمان چهاربعدی مینکوفسکی، بهدلیل اینکه چهار بعد داریم، تانسور متریک را بهشکل یک ماتریس در نظر میگیریم که جز عناصر قطری، سایر عناصر آن صفر هستند:
عبارت وارون است و چون یک ماتریس قطری است، نیز قطری خواهد بود. با این تفاوت که مؤلفههای قطری آن، وارون مؤلفههای قطری است. بنابراین در این فضا-زمان خواهیم داشت:
اکنون با استفاده از این تانسور، مؤلفههای را بهدست میآوریم:
از آنجایی که فقط عناصر قطری تانسور متریک غیرصفر هستند، تنها یک حالت غیرصفر داریم:
سایر مؤلفهها را میتوان بهطور مشابه بهدست آورد:
اگر شکل هموردا و پادوردای تانسور الکترومغناطیسی در هم ضرب شوند، یک کمیت عددی بهدست میآید:
اگر به موضوعات مرتبط با این مطلب علاقهمندید، پیشنهاد میکنیم آموزشهای زیر را نیز ببینید:
^^













عالی بود،ممنون از سایت خوبتون.
میشه در مورد trace of the stress tensor هم توضیح بدید؟
عالی بود
سلام
به نظرم ضرب های انقباضی و دیادیک و … را هم توضیح میدادید بهتر بود.
ممنون
خیلی ساده و سلیس مطالب سطح بالا رو تشریح کردین،دستتون درد نکنه استاد