مخرج مشترک چیست ، چگونه مخرج مشترک بگیریم؟ — به زبان ساده

زمانی که با کسرها سر و کار داریم، محاسبه جمع و تفریق آن‌ها مهم خواهد بود. می‌دانید که هر کسر متعارفی یا عدد گویا از دو بخش تشکیل شده، صورت کسر و مخرج کسر که هر دو مقدار صحیح هستند. برای جمع یا تفریق کردن دو کسر احتیاج داریم که برای هر دو کسر یک مخرج مشترک پیدا کنیم. نحوه محاسبه و بدست آوردن مخرج مشترک در این متن از مجله فرادرس، بررسی و آموزش داده می‌شود.

در این بین پیدا کردن ک م م یا کوچکترین مضرب مشترک هم آموزش داده می‌شود. به همین جهت آشنایی با مفهوم ب م م یا بزرگترین مقسوم علیه مشترک هم ضروری است. برای کسب اطلاعات بیشتر در مورد ضرب و تقسیم اعداد گویا هم می‌توانید تقسیم عدد صحیح — به زبان ساده یا بخش پذیری در اعداد — به زبان ساده و مضرب چیست ؟ — به زبان ساده و با مثال را بخوانید

مخرج مشترک چیست ؟

قبل از اینکه با مخرج مشترک آشنا شویم، به معرفی کسر و اجزای آن می‌پردازیم. به مرور که به پیش برویم، ضرورت ایجاد کسرهایی با مخرج مشترک را بهتر درک خواهیم کرد. به یاد داشته باشید که مخرج مشترک برای مقایسه، جمع و تفریق کسرهای متعارفی لازم هستند.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

صورت و مخرج کسر

همانطور که گفته شد، هر کسر شامل دو بخش است که با خط کسری از یکدیگر جدا می‌شوند. بخش بالایی، صورت نامیده شده و بخش پایینی خط کسری، مخرج است. در تصویر زیر این دو ناحیه مشخص شده‌‌اند.

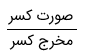
مخرج کسر، نشان می‌دهد که مقدار واحد، به چند بخش تقسیم شده و صورت کسر نشانگر آن است که از این بخش‌ها، چه تعدادی در اختیار ما است.

تصویر زیر معادل کسر $$\dfrac{3}{4}$$ را نشان می‌دهد، زیرا یک شکل واحد (کل پیتزا) به چهار بخش تقسیم شده که فقط سه قسمت آن باقی مانده. بنابراین در این کسر، هدف تعداد بخش‌هایی از کل پیتزا است که هنوز خورده نشده‌اند.

نکته: البته می‌توانستیم از این تصویر برای نمایش کسر $$\dfrac{1}{4}$$ هم استفاده کنیم و بگوییم چه کسری از پیتزا خورده شده.

برای این که یک کسر متعارفی را مشخص کنیم، باید صورت و مخرج کسر، از مجموعه اعداد صحیح باشند. در ادامه بعضی از کسرهای متعارفی مشخص کرده‌ایم. به صورت و کسر آن‌ها توجه کنید. بعضی اوقات ممکن است هم صورت و هم مخرج عدد صحیح مثبت باشند یا یکی از آن‌ها مثبت و دیگری منفی باشند.

$$ \large {\displaystyle {\dfrac { 3}{ 5} }} $$

$$ \large {\displaystyle {\dfrac { -3}{ 5} } }$$

$$ \large {\displaystyle {\dfrac { 3}{ -5} = \dfrac{ -3}{ 5} }} $$

نکته: اگر هم صورت و هم مخرج، منفی باشند، علامت‌های آن‌ها با یکدیگر ساده شده و کل کسر، مثبت خواهد شد. از طرفی اگر فقط صورت یا فقط مخرج کسر، منفی باشند، کل کسر منفی است. بنابراین در چنین حالتی، کسرها یکسان هستند. مورد آخر در رابطه بالا، چنین وضعیتی را نشان داده است.

مقایسه کسرها

حتما می‌دانید که اگر دو کسر با مخرج یکسان داشته باشیم، کسری بزرگتر است که صورت بزرگتری دارد. همینطور در بین دو کسر با مخرج یکسان، کسری کوچکتر است که صورت کوچکتری دارد. به رابطه‌های زیر که برای نشان دادن این موضوع نوشته شده‌اند، توجه کنید.

$$ \large {\displaystyle  \dfrac{ 3}{ 5} >  \dfrac{ 2}{ 5} }$$

$$ \large {\displaystyle  \dfrac{ 6}{ 13} >  \dfrac{ 5}{ 13} }$$

مشخص است که وقتی مخرج‌ها یکسان باشند، کسری که در تعداد تقسیم‌های بیشتری انتخاب شده باشد، بزرگتر است.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

از طرفی اگر در بین و کسر که صورت‌های یکسان دارند، بخواهیم مقایسه انجام دهیم، کسری را بزرگتر در نظر می‌گیریم، که مخرج کوچکتری دارد. زیرا هر چه مخرج کوچکتر باشد، تعداد تقسیم‌ها کمتر است و صورت که تعداد قسمت‌های انتخابی را مشخص می‌کند، بخش‌های بیشتری را شامل می‌شود. به این ترتیب کسری که مخرج بزرگتری داشته باشد، کوچکتر از کسری است که مخرج کوچکتری دارد. این موضوع در رابطه‌ها زیر مشخص شده است.

$$ \large {\displaystyle \dfrac{ 3}{ 5} > \dfrac{ 3}{ 6} }$$

$$ \large {\displaystyle \dfrac{ 6}{ 13} > \dfrac{ 6}{ 15} }$$

همچنین می‌توانیم برای مقایسه بین دو کسر که صورت و مخرج یکسانی ندارند، از این قاعده استفاده کنیم که در بین دو کسر، آن کسری بزرگتر است که صورت بزرگتر یا مخرج کوچکتری داشته باشد.

$$ \large {\displaystyle \dfrac{ 3}{ 5} >  \dfrac{ 2}{ 8} }$$

$$ \large {\displaystyle \dfrac{ 6}{ 13} >  \dfrac{ 4}{ 15} }$$

ولی یک راه‌حل کامل و صحیح برای مقایسه ترتیبی بین کسرها، یکسان کردن مخرج‌های آن‌ها است. به این ترتیب، برای پیدا کردن کسر بزرگتر یا کوچکتر از بین چندین کسر، باید مبنای تقسیم‌ها یعنی مخرج ‌آن‌ها را یکسان کنیم. به این ترتیب همه کسرها، با یک مخرج مشترک نمایش داده می‌شوند و می‌توانیم براساس صورت کسر جدید، آن‌ها را مقایسه کنیم.

محاسبه مخرج مشترک برای کسرها

زمانی که دو کسر دارای مخرج یکسانی باشند، مخرج آن‌ها را مخرج مشترک می‌نامند. ولی به نظر شما، مخرج مشترک، چه اهمیتی دارد؟

همانطور که در قبل مشخص کردیم، داشتن مخرج مشترک یا یکسان برای دو کسر، امکان مقایسه آن‌ها را فراهم می‌سازد. از طرفی محاسبه جمع و تفریق دو کسر با داشتن مخرج مشترک امکان‌‌پذیر است. به همین جهت لازم است، راهکار مربوط به ایجاد مخرج مشترک بین دو کسر را بیاموزیم.

به یاد دارید که با ضرب کردن صورت و مخرج یک کسر در مقدار ثابت (مخالف صفر)، مقدار کسر، تغییری نخواهد کرد. به رابطه‌های زیر توجه کنید.

$$ \large {\displaystyle \dfrac{ 3}{ 5} = \dfrac{ 3 \times 2}{ 5 \times 2} = \dfrac{ 3 \times 4}{ 5 \times 4} = \dfrac{ 3\times 10}{ 5 \times 10}}$$

همه کسرهای بالا، مقدار ثابت و برابر با $$\frac{3}{5}$$ دارند. از همین موضوع برای ایجاد مخرج مشترک استفاده خواهیم کرد.

یکی از شیوه‌هایی که می‌توان به سادگی، مخرج مشترک برای دو کسر ایجاد کرد، استفاده از حاصل‌ضرب مخرج‌ها است. به این معنی که برحسب کسرهای اولیه، کسرهایی جدیدی ایجاد می‌کنیم که مخرج آن‌ها، از حاصل ضرب مخرج کسرهای اولیه ساخته شده است.

واضح است که اگر مخرج کسر اول را در مخرج کسر دوم ضرب می‌کنیم باید صورت آن را هم در مخرج کسر دوم ضرب کنیم تا کسر تغییری نکند.

کافی است همین کار را هم برای کسر دوم انجام دهیم و علاوه بر ضرب مخرج آن در مخرج کسر اول، صورت آن را هم در مخرج کسر اول ضرب کنیم.

این کار را برای مقایسه بین کسرهای مختلف و تعیین کسر بزرگ یا کوچکتر استفاده می‌کنیم. به مثال‌های زیر توجه کنید.

مثال: رابطه بزرگتری یا کوچکتری را در کسر زیر تعیین می‌کنیم.

$$ \large {\displaystyle \dfrac{ 3}{ 5} \; \Box \; \dfrac{ 2}{ 8} }$$

ابتدا مخرج کسر سمت راست را در مخرج کسر سمت چپ ضرب می‌کنیم.

$$ \large {\displaystyle \dfrac{ 2 \times 5}{ 8 \times 5}  = \dfrac{ 10}{ 40} }$$

این کار را برای صورت کسر سمت راست نیز اجرا می‌کنیم.

$$ \large {\displaystyle \dfrac{ 3\times 8}{ 5 \times 8}  = \dfrac{ 24}{ 40} }$$

از آنجا که هر دو کسر، مخرج یکسانی پیدا کرده‌اند، می‌توانیم رابطه بزرگتری یا کوچکتری را مشخص کنیم. چون کسر چپ، صورت بزرگتری نسبت به کسر سمت چپ دارد، بزرگتر خواهد بود.

$$ \large {\displaystyle \dfrac{ 3}{ 5}= \dfrac{ 24 }{ 40} \; > \; \dfrac{ 10}{ 40} = \dfrac{ 2}{ 8} }$$

مثال: رابطه بزرگتری یا کوچکتری را بین کسرهای زیر مشخص کنید.

$$ \large {\displaystyle \dfrac{ 6}{ 13} \; \Box  \; \dfrac{ 4}{ 15} }$$

این بار هم همان عمل قبل را تکرار می‌کنیم و مخرج مشترک بین کسرها را بدست می‌آوریم.

$$ \large {\displaystyle \dfrac{ 6 \times 15}{ 13 \times 15}  = \dfrac{ 90}{ 195} }$$

$$ \large {\displaystyle \dfrac{ 4 \times 13}{ 15 \times 13}  = \dfrac{ 52}{ 195} }$$

چون در بین دو کسر با مخرج برابر، کسری بزرگتر است که صورت بزرگتری دارد، کسر سمت راست، بزرگتر خواهد بود.

$$ \large {\displaystyle \dfrac{ 6}{ 13}= \dfrac{ 90 }{ 195} \; > \; \dfrac{ 52}{ 195} = \dfrac{ 4}{ 15} }$$

در ادامه از این ویژگی برای جمع یا تفریق دو کسر استفاده خواهیم کرد.

مخرج مشترک برای جمع دو کسر

مخرج مشترک علاوه بر مقایسه بین کسرها، برای اجرای عمل جمع و تفریق آن‌ها نیز مفید است. فرض کنید که دو کسر به صورت $$\frac{a}{b}$$ و $$\frac{c}{d}$$ دارید و می‌خواهیم آن‌ها را با هم جمع کنیم.

$$ \large {\displaystyle \dfrac{ a}{ b} + \dfrac{ c}{ d} = ?}$$

فیلم آموزش محاسبات سریع ریاضی در فرادرس

کلیک کنید

طبق روشی که در قبل برای یکسان کردن کسرها و ایجاد مخرج مشترک گفتیم عمل می‌کنیم و کسرهایی با مخرج‌های برابر می‌سازیم.

$$ \large {\displaystyle \dfrac{ a}{ b}  = \dfrac{a \times d}{ b \times d }}$$

$$ \large {\displaystyle \dfrac{ c}{ d}  = \dfrac{ c \times b}{ d \times b }}$$

حال آن‌ها را با یکدیگر جمع می‌کنیم.

$$ \large {\displaystyle \dfrac{ a}{ b} + \dfrac{ c}{ d} = \dfrac{ a \times d}{ b \times d} + \dfrac{ c \times b}{ d \times b} = \dfrac{a \times d + c \times b}{ b \times d} }$$

رابطه ۱: حاصل جمع دو کسر با استفاده از مخرج مشترک

در ادامه به ذکر دو مثال می‌پردازیم که براساس مخرج مشترک، جمع دو کسر انجام شده است.

مثال: برای جمع دو کسر $$\frac{1}{3}$$ و $$\frac{2}{5}$$، از مخرج مشترک باید استفاده کنیم، زیرا مخرج کسرها یکسان نیستند. پس به شیوه‌ای که برای ایجاد مخرج مشترک گفتیم، جمع را اجرا می‌کنیم.

در تصویر زیر مراحل جمع و محاسبه مخرج مشترک را مشاهده می‌کنید. همانطور که می‌بینید، صورت و مخرج کسر اول در مخرج کسر دوم ضرب شده و همینطور، مخرج کسر اول به صورت مضرب صورت و مخرج کسر دوم در آمده است.

به این ترتیب، هر دو مخرج کسرها برابر با ۱۵ شده و این کار باعث می‌شود که مبنای تقسیم بندی هر دو کسر یکسان شوند. پس صورت‌های تبدیل شده این دو کسر را می‌توان با یکدیگر جمع کرد.

$$ \large {\displaystyle \dfrac{ 1}{ 3} + \dfrac{ 2}{ 5} = \dfrac{ 1 \times 5}{ 3 \times 5} + \dfrac{ 2 \times 3}{ 5 \times 3} = \dfrac{ 5}{ 15} + \dfrac{ 6}{ 15} = \dfrac{5 + 6}{ 15} = \dfrac{ 11}{ 15} } $$

مثال: این بار جمع $$\frac{ 1}{ 4} + \frac{ 3}{ 8} $$ را اجرا می‌کنیم. در تصویر زیر مراحل انجام این جمع کسری را مشاهده می‌کنید.

ابتدا کسرها را با یک مخرج یکسان نشان می‌دهیم. کافی است صورت و مخرج کسر اول را در مخرج کسر دوم ضرب کنیم. همین کار را برای کسر دوم هم انجام داده و صورت و مخرج آن را در مخرج کسر اول ضرب می‌کنیم.

$$ \large {\displaystyle \dfrac{ 1}{ 4} + \dfrac{ 3}{ 8} = \dfrac{ 1 \times 8}{ 4 \times 8} + \dfrac{ 3 \times 4}{ 8 \times 4} = \dfrac{ 8}{ 32} + \dfrac{ 12}{ 32} = \dfrac{ 8 + 12}{ 32} = \dfrac{ 20}{ 32} = \dfrac{ 5}{ 8} } $$

نکته: برای ضرب یا تقسیم دو کسر، احتیاجی به مخرج مشترک نیست، زیرا در ضرب، صورت‌ها در هم و مخرج‌ها هم در هم ضرب شده و کسر حاصل ضرب پدید می‌آید. برای تقسیم هم کافی که کسر دوم را به صورت معکوس در آورده و در کسر اول ضرب کنیم تا خارج قسمت تقسیم کسر اول بر دوم بدست آید.

کوچکترین مخرج مشترک

همانطور که در مثال‌های قبل مشاهده کردید، روش پیدا کردن مخرج مشترک، با ضرب مخرج‌ها در یکدیگر صورت گرفت. ولی راه دیگر برای مشترک کردن مخرج‌ها، پیدا کردن کوچکترین مضرب مشترک بین مخرج کسرها است. بنابراین ابتدا مضرب‌ها و روش پیدا کردن کوچکترین مضرب مشترک را شرح می‌دهیم، سپس به کوچکترین مخرج مشترک دو کسر اشاره خواهیم کرد.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

یکی از روش‌های ساده برای محاسبه کوچکترین مضرب مشترک بین دو عدد، نوشتن مضارب آن‌ها است. به این ترتیب از بین مضارب مشترک بدست آمده، کوچکترین را انتخاب می‌کنیم.

مثال: کوچکترین مضرب مشترک بین دو عدد 8 و ۶ را پیدا می‌کنیم. ابتدا مضارب ۸ را از کوچک به بزرگ می‌نویسیم.

۸ × ۱ = ۸,  ۸ × ۲ = ۱۶,  ۸ × ۳ = ۲۴,  ۸ × ۴ = ۳۲,  ۸ × 5 = 40,  ۸ × 6 = 48 ...

همینطور مضارب ۶ را هم به ترتیب مشخص می‌کنیم.

6 × ۱ = ۶, ۶ × ۲ = ۱۲, ۶ × ۳ = 18, 6 × ۴ = 24,  6 × 5 = ۳۰, 6 × 7 = 42, ۶ × 8 = 48 , ...

همانگونه که می‌بینید، ۲۴ و ۴۸ هر دو مضرب‌های مشترک بین ۶ و ۸ هستند. چون کوچکترین آن‌ها، ۲۴ است، آن را کوچکترین مضرب مشترک یا به اصطلاح ک.م.م می‌گوییم.

ک م م – همان‌طور که از نامش پیداست – کوچکترین مضربی است که بین مضارب مشترک دو عدد، قابل مشاهده است. روش دیگر برای پیدا کردن کوچکترین مضرب مشترک بین دو عدد، تجزیه به عوامل اول برای هر دو مخرج است. به این ترتیب، کوچکترین مضرب مشترک بین این دو عدد، برابر با حاصل ضرب عامل‌های مشترک با بزرگترین توان در عامل‌های غیر مشترک است. برای درک بهتر، به مثال زیر توجه کنید.

مثال: کوچکترین مضرب مشترک بین ۶ و ۸ را به شیوه گفته شده، پیدا می‌کنیم. مشخص است که ابتدا باید ۶ و ۸ را به عامل‌های اول تجزیه کرد.

$$ \large {\displaystyle 6 = 2 \times 3 }$$

واضح است که ۶ از ضرب دو عدد اول ۲ و ۳ ساخته شده است. همین کار را برای ۸ نیز انجام می‌دهیم.

$$ \large {\displaystyle 8 = 2 \times  2 \times 2 = 2^3  }$$

حالا طبق رابطه گفته شده، کوچکترین مضرب مشترک آن‌ها را پیدا می‌کنیم.

$$ \large {\displaystyle  2^3 \times 3 = 24  }$$

مثال: کوچکترین مضرب مشترک بین ۱۵ و ۱۸ را بیابید.

$$ \large {\displaystyle 15 = 3 \times 5 }$$

$$ \large {\displaystyle 18 = 2 \times 3 \times 3 = 2 \times 3^2 }$$

به این ترتیب، کوچکترین مضرب مشترک آن‌ها به صورت زیر محاسبه می‌شود.

$$ \large {\displaystyle  5 \times 2 \times 3^2 = 90}$$

پیدا کردن کوچکترین مخرج مشترک با ک.م.م

گفتیم که برای محاسبه جمع یا تفریق دو کسر، باید مخرج آن‌ها را یکسان کنیم. بهتر است که این مخرج یکسان را همان مضرب مشترک مخرج کسرها در نظر بگیریم. سپس کافی است که این مخرج مشترک را بر هر یک از مخرج‌ها تقسیم کرده و در صورت آن‌ها ضرب کنیم.

فرض کنید دو کسر $$\frac{a}{b}$$ و $$\frac{c}{d}$$ به ما داده شده و قرار است که آن‌ها را با هم جمع کنیم. البته در نظر بگیرید که مضرب مشترک برای مخرج‌ها نیز $$m$$ باشد.

$$ \large {\displaystyle \dfrac{ a}{ b} + \dfrac{ c}{ d} = \dfrac{ a \times \dfrac{ m}{ b} }{ m} + \dfrac{ c \times \dfrac{ m}{ d}}{ m} } $$

رابطه 2: فرمول جمع دو کسر با استفاده از کوچکترین مضرب مشترک $$m$$

به مثال‌هایی که در ادامه آورده شده، دقت کنید تا مراحل کار را متوجه شوید.

مثال: حاصل فرمول زیر را به کمک کوچکترین مخرج مشترک بدست می‌آوریم.

$$ \large {\displaystyle \dfrac{ 1}{ 18} + \dfrac{ 1}{ 15}  }$$

از قسمت قبل می‌دانیم که کوچکترین مضرب مشترک بین ۱۸ و ۱۵، همان ۹۰ است. پس در اینجا $$m = 90$$ در نظر گرفته می‌شود. از طرفی هم می‌دانیم که $$a = 1 , b = 18 , c = 1 , d = 15$$ است.

$$ \large {\displaystyle \dfrac{ 1}{ 18} + \dfrac{ 1}{ 15}  = \dfrac{ 1 \times \dfrac{ 90}{ 18} }{ 90} + \dfrac{ 1 \times \dfrac{ 90}{ 15}}{ 90} = \dfrac{ 1 \times 5}{ 90} + \dfrac{ 1 \times 6}{ 90} = \dfrac{ 5 + 6 }{ 90 } = \dfrac{ 11 }{ 90}    }$$

فیلم مجموعه آموزش ریاضیات – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

همانطور که مشاهده می‌کنید، این کسر دیگر احتیاجی به ساده کردن ندارد، زیرا ۱۱ عدد اول است.

مثال: حاصل جمع دو کسر $$\dfrac{ 4}{ 6}$$ و $$\dfrac{ 2}{ 15}$$ را بیابید.

$$ \large {\displaystyle \dfrac{ 2}{ 15} + \dfrac{ 4}{ 6}  }$$

به سادگی می‌توان نشان داد که کوچکترین مضرب مشترک بین ۱۵ و ۶، عدد ۳۰ است. پس در فرمول مربوط به رابطه ۲، مقدار $$m = 30$$ و $$a = 2, b = 15, c = 4 , d = 6$$ قرار می‌دهیم.

$$ \large {\displaystyle \dfrac{ 2}{ 15} + \dfrac{ 4}{ 6} = \dfrac{ 2 \times \dfrac{ 30}{ 15} }{ 30} + \dfrac{ 4 \times \dfrac{ 30}{ 6}}{ 30} = \dfrac{ 4}{ 30} + \dfrac{ 20 }{ 30 } = \dfrac{ 24}{ 30} = \dfrac{ 4}{ 5} } $$

دقت داشته باشید که همه محاسباتی که برای جمع دو کسر و بدست آوردن مخرج مشترک آن‌ها گفتیم برای تفریق یا تفاضل دو کسر نیز صادق است. به همین جهت فقط با دو مثال زیر در مورد تفریق دو کسر متن را ادامه می‌دهیم.

مثال: حاصل رابطه زیر را به کمک کوچکترین مخرج مشترک بدست می‌آوریم.

$$ \large {\displaystyle \dfrac{ 1}{ 18} - \dfrac{ 1}{ 15}  }$$

از رابطه ۲ استفاده کرده ولی به جای علامت جمع از تفریق کمک می‌گیریم.

$$ \large {\displaystyle \dfrac{ 1}{ 18} - \dfrac{ 1}{ 15}  = \dfrac{ 1 \times \dfrac{ 90}{ 18} }{ 90} - \dfrac{ 1 \times \dfrac{ 90}{ 15}}{ 90} = \dfrac{ 1 \times 5}{ 90} - \dfrac{ 1 \times 6}{ 90} = \dfrac{ 5 - 6 }{ 90 } = \dfrac{ -1 }{ 90}    }$$

مثال: حاصل تفریق دو کسر $$\dfrac{ 4}{ 6}$$ و $$\dfrac{ 2}{ 15}$$ را بیابید.

باز هم با استفاده از رابطه ۲ و جایگزینی علامت + با - مسئله را حل می‌کنیم.

$$ \large {\displaystyle \dfrac{ 2}{ 15} - \dfrac{ 4}{ 6}  }$$

$$ \large {\displaystyle \dfrac{ 2}{ 15} - \dfrac{ 4}{ 6} = \dfrac{ 2 \times \dfrac{ 30}{ 15} }{ 30} - \dfrac{ 4 \times \dfrac{ 30}{ 6}}{ 30} = \dfrac{ 4}{ 30} -

\dfrac{ 20 }{ 30 } = \dfrac{ -16}{ 30} = \dfrac{ -8}{ 15} } $$

آزمون مخرج مشترک

در این بخش برای درک بهتر مفهوم مخرج مشترک و چگونگی به‌دست آوردن آن، چند پرسش چهار گزینه‌ای به صورت آزمون مطرح شده است.

خلاصه و جمع‌بندی

محاسبه مخرج مشترک برای جمع و تفریق دو کسر امری ضروری محسوب می‌شود. البته گاهی هم برای مقایسه ترتیب در بین کسرها، آن‌ها را به صورت کسرهایی با مخرج مشترک می‌نویسیم. در این متن به دو شیوه اشاره کردیم که برای پیدا کردن مخرج مشترک در ریاضیات مورد استفاده قرار می‌گیرد. از یک طرف به کمک ضرب مخرج‌ها، کسرهایی با مخرج یکسان ساختیم و از طرف دیگر، با استفاده از مضرب مشترک یا کوچکترین مضرب مشترک، عمل جمع و تفریق کسرها را انجام دادیم.