قضیه تلگان در مدار | به زبان ساده

«قضیه تلگان» (Tellegen's Theorem) در سال ۱۹۵۲ توسط مهندس برق هلندی، «برنارد دی اچ تلگان» (Bernard D.H. Tellegen) معرفی شد. این قضیه در تحلیل شبکه‌های الکتریکی بسیار مفید است. طبق قضیه تلگان، جمع توان‌های لحظه‌ای $$n$$ شاخه یک شبکه الکتریکی صفر است. به عبارت دیگر، جمع انرژی تحویل داده شده به شاخه‌های هر شبكه الکتریکی در هر لحظه از زمان صفر است. قضیه تلگان در طراحی فیلترها در پردازش سیگنال کاربرد فراوانی دارد. قضیه تلگان برای تنظیم پایداری در سیستم عامل‌های پیچیده نیز استفاده می‌شود و در سیستم‌های شیمیایی و بیولوژیکی و برای مشخص بررسی رفتار دینامیکی شبکه فیزیکی کاربرد دارد.

قضیه تلگان مستقل از عناصر شبکه است و برای تحلیل هر شبکه‌ای که از قانون جریان کیرشهف و قانون ولتاژ کیرشهف پیروی می‌کند، قابل اعمال است.

قضیه تلگان

قضیه تلگان را می‌توان برای هر شبکه خطی، غیرخطی، پسیو، اکتیو، متغیر با زمان یا تغییر ناپذیر با زمان، به عنوان مجموع توان (توان لحظه‌ای یا مختلط) صفر بیان کرد.

بنابراین، برای $$n$$ شاخه یک مدار، قضیه تلگان را می‌توان به صورت زیر بیان کرد:

$$\large \sum _ { K = 1 } ^ n {v _ K i _ K } = 0$$

که در آن، $$v _ K$$ ولتاژ شاخه و $$i _ K$$ جریان گذرنده از آن است.

معادله زیر را در نظر بگیرید:

$$\large i _ { p q } = i _ K \;\;\;\;\; ( 1 )$$

این معادله جریان گذرنده از شاخه $$K$$اُم را نشان می‌دهد. همچنین، $$v _ K$$ افت ولتاژ در شاخه $$K$$اُم است و به صورت زیر نوشته می‌شود:

$$\large v _ K = v _ p - v _ q$$

که در آن، $$v_ p$$ و $$v _ q$$، به ترتیب، ولتاژ ‌گره‌های $$p$$ و $$q$$ را نشان می‌دهند.

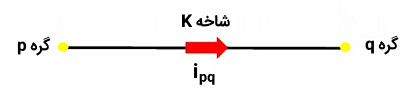
با توجه به رابطه (۱)، داریم:

$$\large v _ K i _ { p q } = ( v _ p - v _ q ) i _ { p q } = v _ K i _ K \;\;\;\;\; ( 2 )$$

همچنین، می‌توان نوشت:

$$\large v _ K i _ K = ( v _ q - v _ p ) i _ { qp } \;\;\;\;\; ( 3 )$$

رابطه زیر به وضوح برقرار است:

$$\large i _ { q p } = - i _ { p q }$$

با جمع کردن دو معادله (۲) و (۳)، داریم:

$$\large 2 v _ K i _ K = ( v _ p - v _ q ) i _{ p q } + ( v _ q - v _ p ) i _ { qp }$$

یا

$$\large v _ K i _ K = \frac 12 \left[ ( v _ p - v _ q ) i _{ p q } + ( v _ q - v _ p ) i _ { qp } \right]$$

این معادلات را می‌توان برای همه شاخه‌های مدار نوشت. با فرض وجود $$n$$ شاخه، معادله زیر را خواهیم داشت:

$$\large \begin {array} { l } \sum _ { K = 1 } ^ { n } v _ { K } i _ { K } = \frac { 1 } { 2 } \sum _ { p = 1 } ^ { n } \sum _ { q = 1 } ^ { n } \left ( v _ { p } - v _ { q } \right ) i _ { p q } \\ \sum _ { K = 1 } ^ { n } v _ { K } i _ { K } = \frac { 1 } { 2 } \sum _ { p = 1 } ^ { n } v _ { p } \left [ \sum _ { q = 1 } ^ { n } i _ { p q } \right ] - \frac { 1 } { 2 } \sum _ { q = 1 } ^ { n } v _ { q } \left [ \sum _ { p = 1 } ^ { n } i _ { p q } \right ] \end {array}$$

اما، طبق قانون جریان کیرشهف (KCL)، جمع جبری جریان‌ها در هر گره برابر با صفر است.

بنابراین، خواهیم داشت:

$$\large \sum _ { p = 1 } ^ { n } i _ { p q } = 0 , \;\;\; \sum _ { q = 1 } ^ { n } i _ { q p } = 0$$

در نتیجه، با توجه به معادله (۴)، می‌توان نوشت:

$$\large \sum _ { K = 1 } ^ { n } v _ { K } i _ K = 0 \;\;\;\;\; (4)$$

بنابراین، مشاهده می‌کنیم که میزان توان تحویل داده شده به شبکه بسته صفر است. این موضوع، قضیه تلگان و همچنین پایستگی توان در هر شبکه الکتریکی را اثبات می‌کند.

همچنین بدیهی است که مجموع توانی که توسط یک منبع مستقل به شبکه منتقل می‌شود، برابر با مقدار توان جذب شده توسط همه عناصر پسیو شبکه است.

تحلیل مدار با استفاده از قضیه تلگان

برای تحلیل مدارهای الکتریکی با استفاده از قضیه تلگان، مراحل زیر را انجام می‌دهیم:

• گام 1. برای استفاده از قضیه تلگان در یک شبکه الکتریکی، اولین گام یافتن افت ولتاژ شاخه‌ها است.
• گام 2. جریان‌های شاخه مربوطه را با استفاده از روش‌های متداول تحلیل مدار پیدا می‌کنیم.
• گام ۳. فرمول قضیه تلگان را با جمع حاصل‌ضرب تمام ولتاژها و جریان‌های شاخه‌ها می‌نویسیم.

به عنوان مثال، اگر شبکه‌ای دارای $$b$$ شاخه باشد، خواهیم داشت:

$$\large \sum _ { K = 1 } ^ { b } v _ { K } i _ { K } = 0$$

کاربردهای قضیه تلگان

کاربردهای مختلف قضیه تلگان به شرح زیر است:

• در سیستم پردازش سیگنال دیجیتال برای طراحی فیلترها استفاده می‌شود.
• در زمینه فرایندهای بیولوژیکی و شیمیایی کاربرد دارد.
• در توپولوژی و ساختار تحلیل شبکه واکنش به کار می‌رود.
• در کارخانه‌های شیمیایی و صنایع نفتی برای تعیین پایداری سیستم‌های پیچیده استفاده می‌شود.

مثال اول قضیه تلگان

مدار شکل زیر را در نظر بگیرید که جهت جریان هر یک از شاخه‌ها به صورت دلخواه و ولتاژ متناظرشان از سر مثبت به سر منفی در نظر گرفته شده است.

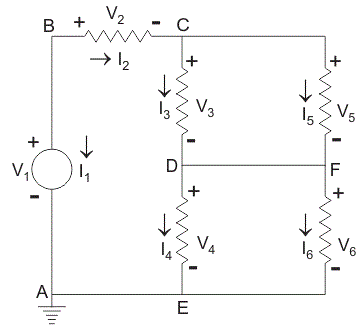
در این مدار، فرض شده است که مجموعه ولتاژهای هر شاخه در قانون ولتاژ کیرشهف و مجموعه جریان‌‌های هر گره در قانون جریان کیرشهف صدق می‌کنند. می‌خواهیم صحت رابطه زیر را که همان قضیه تلگان است، بررسی کنیم:

$$\large \sum _ { k = 1 } ^ n { v _ k } \cdot i _ k = 0$$

در مدار شکل بالا، $$v _ 1$$، $$v _ 2$$ و $$v _ 3$$، به ترتیب، ۷، ۲ و ۳ ولت فرض شده‌اند. با اعمال KVL حول در حلقه ABCDEA، مقدار $$v _ 4 = 2 \, \text{V}$$ به دست می‌آید. در حلقه CDFC نیز مقدار $$v _ 5 = 3 \, \text{V}$$ به دست می‌آید. همچنین در حلقه DFED ولتاژ $$v _ 6 = 2 \, \text{V}$$ را خواهیم داشت.

در ادامه، از KCL استفاده کرده و آن را بر گره‌های B و C و D اعمال می‌کنیم.

در گره B، جریان $$i _ 1 = 5 \, \text{A}$$ و در نتیجه، $$i _ 2 = - 5 \, \text{A}$$ را خواهیم داشت. در گره C جریان $$i _ 3 = 3 \, \text{A}$$ و در نتیجه، $$i _ 5 = - 8 \, \text{A}$$ را داریم. در گره D نیز جریان $$i _ 4 = 4 \, \text {A}$$، جریان $$i _ 6 = - 9 \, \text {A}$$ را نتیجه خواهد داد. با توجه به مقادیر ولتاژ و جریانی که به دست آوردیم، خواهیم داشت:

$$\large 7 \times 5 + 2 \times ( - 5 ) + 3 \times 3 + 2 \times 4 + 3 \times ( - 8 ) + 2 \times ( - 9 ) = 0$$

که صحت قضیه تلگان را نشان می‌دهد:

$$\large \sum _ { k = 1 } ^ { n } v _ { k } \cdot i _ { k } = 0$$

مثال دوم قضیه تلگان

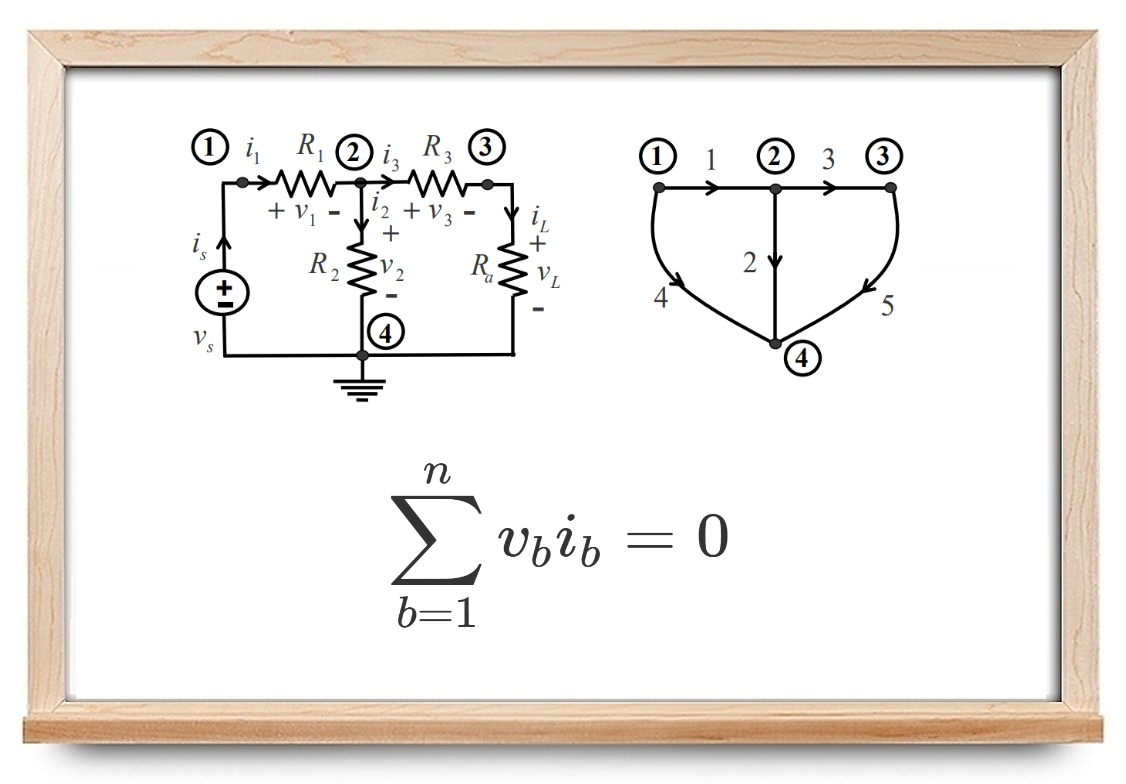
دو مدار $$N$$ و $$\hat { N}$$ را در نظر بگیرید. فرض کنید $$v _ j$$ و $$i _ j$$ ولتاژ و جریان شاخه $$j$$اُم مدار $$N$$ باشند.

فیلم آموزش مدارهای الکتریکی ۱ – جامع و کاربردی در فرادرس

کلیک کنید

همچنین $$\hat{v} _ j$$ و $$\hat { i } _ j$$ ولتاژ و جریان مدار $$\hat { N}$$ را نشان می‌دهند. مقادیر $$R _ 1$$، $$R_ 2$$ و $$R_ 3$$ در هر دو مدار معلوم هستند. همچنین، $$i _ s = 1\, \text{A}$$ و $$v _ L = 2 \, \text{V}$$ را برای $$N$$ و $$\hat { v } _ s = 3 \, \text{V}$$ را برای $$\hat { N}$$ داریم. می‌خواهیم ولتاژ $$\hat { v } _ L$$ مدار $$\hat { N}$$ را به دست آوریم.

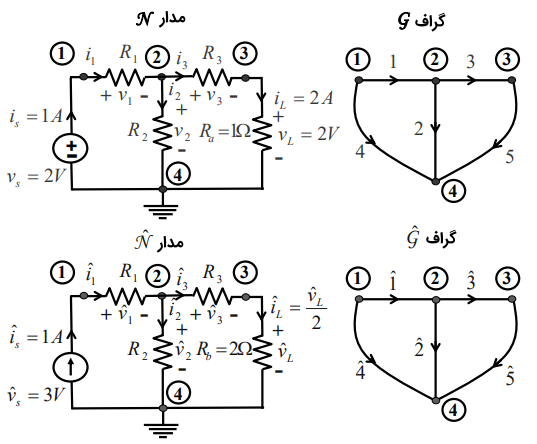
اگرچه دو مدار متفاوت هستند ($$N$$ با منبع ولتاژ تحریک می‌شود، اما $$\hat {N}$$ با منبع جریان کار می‌کند؛ همچنین مقادیر $$R_ a$$ و $$R _ b$$ متفاوت هستند)، گراف آن‌ها یکسان است.

ار آنجا که دو گراف $$G$$ و $$\hat { G }$$ مشابه هستند، می‌توانیم قضیه تلگان را برای هر مجموعه‌ ولتاژ در $$N$$ که در KVL صدق می‌کند و هر مجموعه جریان در $$\hat { N}$$ که در KCL صدق می‌کند و بالعکس، اعمال کنیم؛ البته با در نظر گرفتن این نکته که باید از قرارداد مرجع مربوطه استفاده کنیم:

برای $$N$$:

$$\large v_{4}=2 V, \;\; i_{4}=-1 A$$

برای $$\hat{N}$$:

$$\large \hat{v}_{4}=3 V, \;\; \hat{i}_{4}=-1 A$$

(الف) اعمال قضیه تلگان با استفاده از جواب‌های ولتاژ $$v _ j$$ برای $$N$$ (که باید در KVL صدق کنند) و جواب‌های جریان $$\hat {i} _ j$$ برای $$\hat {N}$$ (که باید در KCL صدق کنند):

$$\large \underbrace { \left ( v _ { 1 } \right ) \left ( \hat { i } _ { 1 } \right ) + \left ( v _ { 2 } \right ) \left ( \hat { i } _ { 2 } \right ) + \left ( v _ { 3 } \right ) \left ( \hat { i } _ { 3 } \right ) } + \left ( v _ { 4 } \right ) \left ( \hat { i } _ { 4 } \right ) + \left ( v _ { 5 } \right ) \left ( \hat { i } _ { 5 } \right ) = 0 \\ \large \Rightarrow \quad I = \sum _ { j = 1 } ^ { 3 } \left ( v _ { j } \right ) \left ( \hat { i } _ { j } \right ) \quad + ( 2 ) ( - 1 ) + ( 2 ) \left ( \frac { \hat { v } _ { L } } { 2 } \right ) = 0 \;\;\;\;\;(5)$$

(ب) اعمال قضیه تلگان با استفاده از جواب‌های ولتاژ $$\hat{v} _ j$$ برای $$\hat{N}$$ (که باید در KVL صدق کنند) و جواب‌های جریان $${i} _ j$$ برای $${N}$$ (که باید در KCL صدق کنند):

$$\large \underbrace { \left ( \hat { v } _ { 1 } \right ) \left ( i _ { 1 } \right ) + \left ( \hat { v } _ { 2 } \right ) \left ( i _ { 2 } \right ) + \left ( \hat { v } _ { 3 } \right ) \left ( i _ { 3 } \right ) } + \left ( \hat { v } _ { 4 } \right ) \left ( i _ { 4 } \right ) + \left ( \hat { v } _ { 5 } \right ) \left ( i _ { 5 } \right ) = 0 \\ \large \Rightarrow \quad \quad \hat { I } = \sum _ { j = 1 } ^ { 3 } \left ( \hat { v } _ { j } \right ) \left ( i _ { j } \right ) \quad + ( 3 )( - 1 ) + \left ( \hat { v } _ { L } \right ) ( 2 ) = 0 \;\;\;\;\; (6 )$$

با توجه به روابط بالا، داریم:

$$\large \begin {align*} I & =\sum _ { j = 1 } ^ { 3 } \left ( v _ { j } \right ) \left ( \hat { i } _ { j } \right ) = \left ( R _ { 1 } i _ { 1 } \right ) \left ( \hat { i } _ { 1 } \right ) + \left ( R _ { 2 } i _ { 2 } \right ) \left ( \hat { i } _ { 2 } \right ) + \left ( R _ { 3 } i _ { 3 } \right ) \left ( \hat { i } _ { 3 } \right ) \;\;\;\;\; (7)\\ I & = \sum _ { j = 1 } ^ { 3 } \left ( \hat { v } _ { j } \right ) \left ( i _ { j } \right ) = \left ( R _ { 1 } \hat { i } _ { 1 } \right ) \left ( i _ { 1 } \right ) + \left ( R _ { 2 } \hat { i } _ { 2 } \right ) \left ( i _ { 2 } \right ) + \left ( R _ { 3 } \hat { i } _ { 3 } \right ) \left ( i _ { 3 } \right ) \;\;\;\;\; (8) \\ & \Rightarrow \quad I = \hat { I } \end {align*}$$

با محاسبه تفاضل $$(5)-(6)$$، خواهیم داشت:

$$\large \left [ ( 2 ) ( - 1 ) + ( 2 ) \left ( \frac { \hat { v } _ { L } } { 2 } \right ) \right ] - \left [ ( 3 )( - 1 ) + \left ( \hat { v } _ { L } \right ) ( 2 ) \right ] = 0 \\ \large \begin {array} { c } - 2 + \hat { v } _ { L } + 3 - 2 \hat { v } _ { L } = 0 \\ \Rightarrow \quad \hat { v } _ { L } = 1 V \end {array}$$