توان الکتریکی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

احتمالاً تاکنون از خود پرسیدهاید که فرمولهای توان الکتریکی با هم چه ارتباطی دارند یا تفاوت بین توانهای DC ،AC و مختلط چیست و چگونه میتوان آنها را با مفروضات فیزیکی انرژی و توان تطبیق داد. در این آموزش، به همه این پرسشها پاسخ خواهیم داد.
تعریف
طبق یک تعریف رسمی و متداول، هر شکلی از توان (الکتریکی، مکانیکی، گرمایی و..) برابر با نرخ انرژی یا کاری است که مصرف یا انجام میشود. واحد استاندارد توان، «وات» (Watt) یا «ژول بر ثانیه» است. توان الکتریکی یک بار، نرخ انرژی الکتریکی است که - از طریق یک مدار الکتریکی - به آن تحویل داده میشود و به شکل دیگری از انرژی (مانند گرما، نور، صدا، شیمیایی، جنبشی و..) تبدیل میشود. توان را بر حسب کمیتهای الکتریکی ولتاژ و جریان، میتوان با فرمول استاندارد زیر محاسبه کرد:
$$ \large P = V I $$
که در آن، $$ P $$ توان بر حسب وات، $$V$$ ولتاژ بر حسب ولت و $$I$$ جریان بر حسب آمپر است.
توان DC
در قرن نوزدهم میلادی، فیزیکدان انگلیسی، «جیمز پرسکات ژول» (James Prescott Joule) مشاهده کرد که مقدار انرژی گرمایی $$ H $$ که توسط جریان الکتریکی ثابت $$I$$ در مادهای با مقاومت $$ R $$ در زمان $$t$$ تلف میشود، در رابطه مستقیم زیر صدق خواهد کرد:
$$ H \propto I ^ { 2 } R t $$
از آنجایی که توان، نرخ تغییر انرژی در طول زمان است ($$ P = \Delta H / \Delta t $$)، مشاهدات ژول را برای توان الکتریکی میتوان به صورت زیر نوشت:
$$ \large P \propto I ^ { 2 } R $$
اکنون با اعمال قانون اهم ($$ R = V / I $$)، میتوانیم رابطه زیر را بنویسیم:
$$ \large P \propto V I $$
واحد SI انرژی، ژول است. برای انرژی الکتریکی، یک ژول به عنوان مقدار کاری تعریف میشود که برای حرکت یک بار الکتریکی به اندازه یک کولن، در یک اختلاف پتانسیل یک ولتی لازم است. به عبارت دیگر، رابطه زیر برقرار است:
$$ \large E = Q V $$
که در آن، $$E$$ انرژی الکتریکی بر حسب ژول، $$ Q$$ بار بر حسب کولن و $$V$$ اختلاف پتانسیل بر حسب ولت است.
جریان الکتریکی نیز به عنوان مقدار باری تعریف میشود که در واحد زمان عبور میکند ($$I = Q / t $$). بنابراین، داریم:
$$ \large E = V I t $$
از آنجایی که توان، نرخ تغییر انرژی در واحد زمان است، رابطه بالا را میتوان به صورت زیر نوشت:
$$ \large P = V I $$
رابطه خیر، همان رابطه معروف توان الکتریکی است که بیان کردیم.
توان AC
همانطور که گفتیم، معادله توان در حالت DC به صورت $$ P = V I $$ است. این رابطه را فقط در مدارهای جریان مستقیم و برای شکل موجهای DC میتوان به کار برد. در مدارهای AC یا برای شکل موجهای جریان متناوب، مقدار لحظهای شکل موج همواره در طول زمان تغییر میکند. بنابراین، توان AC از نظر مفهومی کمی با توان DC متفاوت است.
شکل موجهای AC در سیستمهای قدرت، معمولاً سینوسی و به شکل زیر هستند (برای ولتاژ):
$$ \large v ( t ) = V \cos ( \omega t - \phi ) $$
که در آن، $$V$$ دامنه شکل موج ولتاژ بر حسب ولت، $$ \omega = 2 \pi f $$ فرکانس زاویهای بر حسب رادیان بر ثانیه، $$ \phi $$ جابهجایی زاویه بر حسب رادیان و $$ f $$ فرکانس است. ولتاژ $$v (t ) $$، مقدار لحظهای ولتاژ بر حسب ولت در زمان دلخواه $$t $$ (بر حسب ثانیه) است.
اگر جریان $$ i (t) $$ شکل مشابهی با ولتاژ داشته باشد، واضح است که توان لحظهای $$ p ( t ) = v ( t ) i ( t ) $$ با زمان تغییر خواهد کرد.
فرض کنید شکل موجهای جریان و ولتاژ، هر دو سینوسی بوده و اختلاف فاز آنها به گونهای است که جریان، با زاویه فاز $$ \theta $$ از ولتاژ عقبتر باشد. بنابراین، ولتاژ و جریان را میتوان به صورت زیر نوشت:
$$ \large \begin {align*} v ( t ) & = V \cos ( \omega t ) \\
i ( t ) & = I \cos ( \omega t - \theta ) \end {align*} $$
در نتیجه، توان لحظهای را با کمی عملیات ریاضی میتوان به شکل زیر نوشت:
$$ \large \begin {align*} p ( t ) & = v ( t ) i ( t ) \\
& = V \cos (\omega t ) I \cos ( \omega t - \theta ) \\
& = \frac { V I } { 2 } ( \cos \theta + \cos ( 2 \omega t - \theta) ) \\
& = \frac { V I } { 2 } ( \cos \theta + \cos ( 2 \omega t ) \cos \theta + \sin ( 2 \omega t ) \sin \theta ) \\
& = \frac { V I } { 2 } ( \cos \theta ( 1 + \cos ( 2 \omega t ) ) + \sin ( 2 \omega t ) \sin \theta ) \end {align*} $$
از آنجایی که مقدار مؤثر (جذر میانگین مربع) ولتاژ و جریان به ترتیب، $$ V _ { r m s } = \frac { V } { \sqrt { 2 } } $$ و $$ I _ { r m s } = \frac { I } { \sqrt { 2 } } $$ است، توان به صورت زیر نوشته میشود:
$$ \large p ( t ) = V _ { r m s } I _ { r m s } ( \cos \theta ( 1 + \cos ( 2 \omega t ) ) + \sin ( 2 \omega t ) \sin \theta ) $$
میتوانیم معادله فوق را با تعاریف زیر، به شکل سادهتر نیز بنویسیم:
$$ \large P = V _ { r m s } I _ { r m s } \cos \theta $$
و
$$ \large Q = V _ { r m s } I _ { r ms } \sin \theta $$
در نتیجه، معادله توان لحظهای AC به فرم زیر نوشته میشود:
$$ \large p ( t ) = P ( 1 + \cos ( 2 \omega t ) ) + Q \sin ( 2 \omega t ) $$
جمله $$ P $$ «توان اکتیو» (Active Power) یا «توان حقیقی» (Real Power) و $$ Q$$ «توان راکتیو» (Reactive Power) نامیده میشود. همچنین، جمله $$ \cos \theta $$، «ضریب توان» (Power Factor) نام دارد و نشان دهنده درصد توان حقیقی از توان AC است که تحویل داده میشود. توان اکتیو، مؤلفهای از توان است که میتواند کار واقعی انجام دهد (مثلاً به شکل مفیدی از انرژی، مانند مکانیکی، گرما یا نور تبدیل شود).
تفسیر فیزیکی
معادله اصلی توان را در نظر بگیرید:
$$ \large p ( t ) = \frac { V I } { 2 } \left [ \cos \theta + \cos ( 2 \omega t - \theta ) \right ] $$
با توجه به شکل زیر میتوان فهمید که شکل موج توان، سینوسی است و فرکانس آن، دو برابر فرکانس ولتاژ و جریان است.

معادله توان را میتوانیم به دو بخش زیر تفکیک کنیم:
- یک جمله ثابت (توان اکتیو): $$ V _ { r m s} I _ { r m s } \cos \theta $$
- یک جمله متناوب: $$ V _ { r m s } I _ { r m s } \cos ( 2 \omega t - \theta ) $$
شکل زیر، نمودار مربوط به این دو بخش را به تفکیک نشان میدهد.
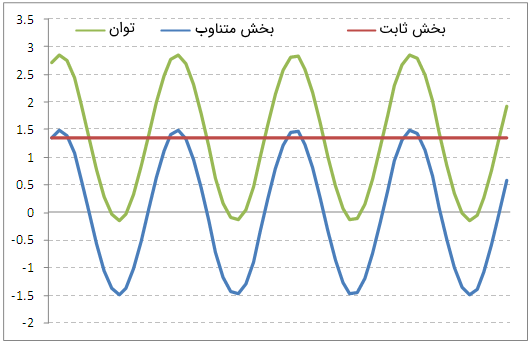
توجه کنید که جمله متناوب، همواره حول صفر نوسان میکند و جمله ثابت، به ضریب توان بستگی دارد. اما مفهوم ضریب توان $$ \cos \theta $$ چیست؟
ضریب توان
همانطور که گفتیم، ضریب توان به صورت کسینوس زاویه توان (اختلاف فاز بین ولتاژ و توان) یا $$ \cos \theta $$ تعریف میشود. گاهی ضریب توان را با واژههای پیشفاز (Leading) و پسفاز (Lagging) بیان میکنند. زاویه توان، فقط در بازه $$-90 ^ \circ$$ و $$+90^ \circ$$ تغییر میکند. کسینوس یک زاویه در ربع چهارم، مثبت است و بنابراین، ضریب توان نیز همیشه مثبت خواهد بود. بنابراین، تنها راه تشخیص مثبت یا منفی بودن زاویه توان، پیشفاز یا پسفاز بودن ضریب توان است:
- ضریب توان پسفاز: وقتی جریان عقبتر از ولتاژ باشد، بدین معنی است که شکل موج جریان، نسبت به شکل موج ولتاژ تأخیر دارد و دیرتر به یک نقطه زمانی خاص میرسد. در این حالت، زاویه توان مثبت است.
- ضریب توان پیشفاز: در این حالت، جریان جلوتر از ولتاژ است؛ بدین معنی که شکل موج جریان، نسبت به شکل موج ولتاژ تقدم دارد و زودتر به یک نقطه زمانی خاص میرسد. در این حالت، زاویه توان منفی است.
- ضریب توان واحد: حالتی است که در آن، جریان و ولتاژ، فاز مشابهی دارند.
اهمیت ضریب توان، در امپدانس بار است. بارهای سلفی یا القایی (مانند سیمپیچها، موتورها و..) ضریب توان پسفاز دارند. در مقابل، ضریب توان بارهای خازنی (مانند خازنها)، پیشفاز است. بارهای مقاومتی (مانند هیترها) نیز ضریب توان واحد دارند.
ارتباط با انرژی
طبق تعریف، توان، نرخ انجام کار یا نرخ مصرف انرژی است. از آنجایی که توان AC با زمان تغییر میکند، مقدار انرژی تحویلی توان در زمان T، با انتگرالگیری از تابع توان AC در زمان به دست میآید:
$$ \large E = \int _ { 0 } ^ { T } p ( t ) d t $$
همانطور که گفتیم، توان AC از دو بخش توان ثابت $$ V _ { r m s } I _{ r m s} \cos \theta $$ و توان متناوب $$ V _ { r m s } I _ { r m s } \cos ( 2 \omega t - \theta ) $$ تشکیل میشود. بنابراین، انتگرال را میتوان به صورت زیر نوشت:
$$ \large E = \int _ { 0 } ^ { T } V _ { r m s } I _ { r m s } \cos \theta d t + \int _ { 0 } ^ { T } V _ { r m s } I _ { r m s } \cos ( 2 \omega t - \theta ) d t $$
فرض کنید از یک دوره تناوب شکل موج AC (یعنی $$ T = \frac{\pi}{\omega} $$) انتگرال میگیریم. بنابراین، بخش متناوب انتگرال حذف میشود و حاصل انتگرال اصلی، به صورت زیر خواهد بود:
$$ \large E = V _ { r m s } I _ { r m s } \cos \theta . \frac { \pi }{ \omega } $$
از رابطه بالا در مییابیم که کار، تنها توسط توان اکتیو انجام میشود و کار خالص توان راکتیو صفر است.
توان مختلط
در بسیاری از مراجع، توان AC با کمیتهای مختلط بیان میشود؛ زیرا ویژگیهای جذابی برای تحلیل دارند (از جبر برداری استفاده میکنند). اما اغلب، «توان مختلط» (Complex Power) به سادگی و بدون استخراج معادلات تعریف میشود. اما اعداد مختلط چگونه کمیتهای توان را نشان میدهند؟
در سال ۱۸۹۷، «چارلز پرتیوس استینمتز» (Charles Proteus Steinmetz) در کتابش با نام «نظریه و محاسبه پدیده جریان متناوب»، نمایش شکل موجهای AC را با کمیتهای مختلط پیشنهاد کرد.
در بخشهای قبل، فرم عمومی توان AC را به دست آوردیم (برای ضریب توان پسفاز):
$$ \large p ( t ) = \frac { V I } { 2 } \left [ \cos \theta + \cos ( 2 \omega t - \theta ) \right ] $$
که در آن، $$V$$ و $$I$$ مقادیر دامنه ولتاژ و جریان هستند.
برای فرکانس زاویهای ثابت $$ \omega $$، این شکل موج را میتوان با دو پارامتر مشخص کرد: یکی ضرب ولتاژ مؤثر در جریان مؤثر و دیگری زاویه پسفاز $$ -\theta $$.
با استفاده از این دو پارامتر، میتوانیم شکل موج AC توان $$p(t)$$ را با بردار دو بعدی S بیان کنیم که در مختصات قطبی، با اندازه $$ VI$$ و زاویه قطبی $$ -\theta $$ تعریف میشود.
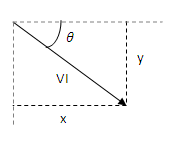
این بردار $$ \boldsymbol{S} $$ را میتوان به یک زوج در مختصات دکارتی تبدیل کرد:
$$ \large \begin {align*}
x & = V I \cos \theta \\
y & = -V I \sin\theta
\end {align*}$$
با استفاده از مثلثات میتوان نشان داد که جمع و تفریق بردارهای توان AC از قواعد کلی حساب برداری تبعیت میکند؛ یعنی مؤلفههای مستطیلی دو یا چند تابع سینوسی را میتوان با هم جمع یا از هم کم کرد (اما نمیتوان آنها را در هم ضرب یا بر هم تقسیم کرد).
البته کار با هر مؤلفه مستطیلی به تنهایی میتواند سخت یا غیرممکن باشد. فرض کنید مؤلفههای مستطیلی $$x $$ و $$y$$ را با استفاده از عملگر بیمعنی $$ j$$ تفکیک کنیم. بنابراین، بردار $$ \boldsymbol{S} $$ به صورت زیر خواهد بود:
$$ \large \begin {align*}
\boldsymbol { S } & = x + j y \\
\boldsymbol { S } & = V I \cos \theta - j V I \sin \theta
\end {align*}$$
توجه کنید که علامت جمع (+) در عبارت بالا یک علامت ساده نیست، زیرا $$x$$ و $$y$$ کمیتهای متعامدی در فضای دو بعدی هستند. نماد $$j$$، یک عملگر بیمعنی برای تمایز مؤلفه عمودی $$y$$ است.
فرض کنید بردار را $$ 90 ^ \circ $$ میچرخانیم:
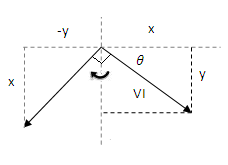
بردار بعد از چرخش به صورت زیر است:
$$ \large \boldsymbol { S } ^ \prime = - y + j x $$
حال عملگر $$j$$ را برای چرخش $$ 90 ^ \circ $$ به گونهای تعریف میکنیم که ضرب بردار $$V$$ در $$j$$ بردار را به اندازه $$90 ^ \circ $$ بچرخاند. بنابراین، داریم:
$$ \large j \boldsymbol { S } = \boldsymbol { S } ^ \prime $$
$$ \large j x + j ^ { 2 } y = - y + j x $$
$$ \large j ^ { 2 } + 1 = 0 \\
j = \sqrt { - 1 } $$
در نتیجه، با تعریف $$j$$ به عنوان عملگر چرخش $$90$$ درجهای، $$j$$ یک عدد موهومی خواهد بود و بردار $$ \boldsymbol{S} = x + jy $$ یک مقدار مختلط است. بنابراین، بردار $$ \boldsymbol {S} $$ را میتوان به صورت زیر نوشت:
$$ \large \boldsymbol { S } = V I \cos \theta - j V I \sin \theta $$
عبارت بالا را توان مختلط یا گاهی «توان ظاهری» (Apparent Power) مینامند. توان ظاهری برای ضریب توان پسفاز و پیشفاز به صورت زیر خواهد بود:
برای ضریب توان پسفاز: $$ \large \boldsymbol { S } = P - j Q $$
برای ضریب توان پیشفاز : $$ \large \boldsymbol { S } = P + j Q $$
که در آن، $$ P = VI\cos\theta $$ و $$ Q = VI\sin\theta $$ به ترتیب، مقادیر توان اکتیو (یا حقیقی) و توان راکتیو هستند.
توان مختلط فازورها
فرض کنید فازورهای ولتاژ و جریان زیر را داریم:
$$ \large \begin {align*}
\boldsymbol { V } & = V \angle \phi \\
\boldsymbol { I } & = I \angle \delta
\end {align*}$$
بنابراین، توان مختلط $$ \boldsymbol{S} $$ را میتوان به صورت زیر محاسبه کرد:
$$ \large \begin {align*}
\boldsymbol { S } & = \boldsymbol { V } \boldsymbol { I } ^ { * } \\
& = V \angle \phi \times I \angle (-\delta) \\
& = VI \angle (\phi - \delta) \\
& = VI \angle (\theta) = VI\cos\theta - jVI\sin\theta \\
\end {align*}$$
که در آن، $$ \theta = \phi - \delta $$ زاویه توان (یعنی اختلاف فاز بین ولتاژ و جریان) است.
نماییهای مختلط
با استفاده از فرمول اویلر میتوانیم بردار توان مختلط را به عنوان نمایی مختلط نمایش دهیم:
$$ \large S = V I e ^ { - j \theta } $$
با استفاده از نماییهای مختلط، میتوان از راهی جایگزین برای بیان توان مختلط استفاده کرد. دیدیم که وقتی زاویه فاز $$ \theta $$ تغییر کند، بردار $$ \boldsymbol{S} $$ حول مبدأ میچرخد. در حقیقت، نمایی مختلط $$ e^{j\theta} $$ یک عملگر برای چرخش بردارها حول دایرهای در فضای دو بعدی است. بنابراین، $$ S = VI e^{-j\theta} $$ یک بردار با اندازه $$VI$$ است که به اندازه $$ P = \theta $$ در جهت عقربههای ساعت چرخیده است.
به عبارت دیگر، توان مختلط یک نمایش برداری دو بعدی از توان AC است که کار کردن با آن، نسبت به تابع زمانی $$p(t) $$ آسانتر است.
توان الکتریکی ظاهری
در بخش قبل دیدیم که توان مختلط $$ \boldsymbol{S} $$ گاهی توان ظاهری نیز نامیده میشود. هرچند در عمل، توان ظاهری اغلب برای بیان اندازه $$ \boldsymbol{S} $$، یعنی $$ |\boldsymbol{S}| = VI $$ به کار میرود.
توان سه فاز
تا اینجا، با مفاهیم و روابط توان DC و توان AC تکفاز آشنا شدیم. توان در یک سیستم سه فاز متعادل، برابر با مجموع توانهای هر یک از فازها است؛ یعنی:
$$ \large P _ { 3 \phi } = 3 V _ { p h } I _ { p h } \cos \theta $$
که در آن، $$ P_{3\phi} $$ توان اکتیو سه فاز بر حسب وات (W)، $$ V_{ph} $$ ولتاژ فاز-خنثی برحسب ولت (V)، $$ I_{ph} $$ جریان فاز بر حسب آمپر (A) و $$ \cos\theta $$ ضریب توان است.
برای یک بار با اتصال ستاره، داریم:
$$ \large V _ { p h } = \frac { V _ { l } } { \sqrt { 3 } } $$
و
$$ \large I _ { p h } = I _ { l } $$
برای بار با اتصال مثلث نیز روابط زیر برقرار است:
$$ \large V _ { p h } = V _ { l } $$
و
$$ \large I _ { p h } = \frac { I _ { l } } { \sqrt { 3 } } $$
در روابط بالا، $$V _l $$ و $$I_l $$ به ترتیب، ولتاژ و جریان خط به خط هستند.
بنابراین، توان اکتیو سه فاز، برای بارهای ستاره و مثلث بر حسب مقادیر ولتاژ و جریان خط به صورت زیر خواهد بود:
$$ \large \begin {align*}
P _ { 3 \phi } & = 3 V _ { p h } I _ { p h } \cos \theta \\
& = \frac { 3 } { \sqrt { 3 } } V _ { l } I _ { l } \cos \theta \\
& = \sqrt { 3 } V _ { l } I _ { l } \cos \theta
\end {align*}$$
به طریق مشابه، توان راکتیو و توان ظاهری سه فاز با روابط زیر محاسبه میشوند:
$$ \large \begin {align*}
Q _ { 3 \phi} & = \sqrt { 3 } V _ { l } I _ { l } \sin \theta \\
S _ { 3 \phi } & = \sqrt { 3 } V _ { l } I _ { l }
\end {align*}$$
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- پخش بار در سیستم قدرت — مفاهیم و معادلات
- مغناطیس چیست؟ — به زبان ساده
- سیستم کنترل حلقه بسته — به زبان ساده
^^











سلام و عرض ادب
در مبحث مدار سه فاز داشتیم که در اتصال ستاره ولتاژ خط نسبت به ولتاژ فاز هم بزرگتره هم پیش فازه.در هنگام تبدیل ولتاژ خط به فاز و بلعکس اون ضریب رادیکال 3 رو در نظر میگیرن ولی اختلاف فاز رو نه…میخواستم بدونم به چه علتی!!!
همین سوال در مورد جریان فاز و خط در اتصال مثلث وجود داره.ممنون میشم جواب بدین
سلام پژمان عزیز.
اختلاف فاز بین ولتاژ و جریان است که در محاسبه توان اهمیت پیدا میکند، نه اختلاف فاز جریان فاز و خط.
سپاس از همراهیتان با مجله فرادرس.
در بخش «توان مختلط» گفته شده «که در آن،
V و I مقادیر RMS ولتاژ و جریان هستند.» که فکر میکنم اشتباه است و مقادیر پیک هستند.
سلام.
متن بازبینی و اصلاح شد.
سپاس از همراهی و بازخوردتان.
درود
خسته نباشید استاد عزیز.واقعا از اموزش های عالی شما استفاده میکنیم.
سلام میخواستم بپرسم علامت ستاره توی توان یکی از فرمول های درس سیستم های قدرت به چه معنیه
سلام.
علامت ستاره در این فرمول به معنی مزدوج مختلط است.
سالم و سربلند باشید.
سلام
سوال من درمورد پیک پاور و اوریج پاور (پاور میانگین)هست.فرق این دو در چیست و با پیدا کردن این دو مقدار چه اطلاعاتی به دست می آوریم؟ با تشکر
استاد سلام یه سوال داشتم!
رو شارژر فندکی خودرو زده خروجی: ۲.۴آمپر (میدونیم ولتاژ باطری خودرو حدود ۱۲ ست)
با این تفاسیر و فرمول ذکرشده w=Av ،توان میشه ۲۸.۸ وات!!
درصورتی که روی دستگاه وات خروجی رو ۱۲ معرفی کرده!
من اشتباه می کنم یا شرکت سازنده؟؟
سلام.
در مدار شارژر فندکی یک مبدل باک (کاهنده ولتاژ) وجود دارد که ولتاژ ۱۲ ولت باتری خودرو را به ۵ ولت تبدیل میکند تا به سطح مناسبی برا استفاده USB از آن برسد. اگر ۲٫۴ آمپر را در ۵ ولت ضرب کنیم، به همان ۱۲ وات میرسیم که شرکت سازنده ارائه کرده است.
شاد و پیروز باشید.