قضیه تفکیک لبگ در نظریه اندازه — به زبان ساده

در ریاضیات و بخصوص نظریه اندازه (Measure Theory)، قضیه تجزیه یا تفکیک لبگ (Lebesgue's Decomposition theorem) نقش مهمی ایفا میکند و نتایج و قضیههای متعددی از آن بهره میبرند. این قضیه نشان میدهد که هر اندازه علامتدار سیگما-متناهی را میتوان به دو اندازه علامت دار سیگما متناهی دیگر تفکیک کرد که نسبت به یک اندازه دیگر مطلقا پیوسته باشد. اهمیت این موضوع بخصوص در نظریه احتمال (Probability Theory) محسوس است. به همین دلیل این نوشتار از مجله فرادرس را به قضیه تفکیک لبگ در نظریه اندازه اختصاص دادهایم.
برای آشنایی بیشتر با نظریه احتمال و اندازه بهتر است نوشتارهای دیگر مجله فرادرس با عنوان نظریه اندازه در ریاضیات — مفاهیم و کاربردها و نظریه احتمال و کاربردهای آن — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای تجزیه هان و کاربردهای آن — به زبان ساده و قضیه رادون نیکودیم و اثبات آن — به زبان ساده نیز خالی از لطف نیست.
قضیه تفکیک لبگ در نظریه اندازه
قضیه تفکیک لبگ نشان میدهد که در نظریه اندازه، هر اندازه سیگما-متناهی را میتوان به صورت حاصل جمع دو یا سه اندازه دیگر نوشت. در ضمن این قضیه شرایط این تفکیک و همینطور خصوصیات اندازههای تفکیکی را مشخص و معین میکند. این موضوع بخصوص در تفکیک یک فرآیند تصادفی در نظریه احتمال اهمیت دارد. در انتهای این نوشتار این موضوع را هم مورد بررسی قرار خواهیم داد. ولی از آنجایی که در قضیه تفکیک لبگ مفاهیم مهم و متنوعی از نظریه اندازه مورد بحث قرار میگیرد، ابتدا آنها را شرح داده، سپس به تفکیک لبگ به صورت کامل خواهیم پرداخت. ابتدا موضوعاتی که در فهرست زیر قرار گرفتهاند را بیشتر مورد تحلیل قرار میدهیم.
- معرفی اندازه سیگما-متناهی
- معرفی اندازه علامت دار
- معرفی اندازه مطلقا پیوسته
- معرفی اندازه سیگما-متناهی
- معرفی اندازههای منفرد
معرفی اندازه سیگما-متناهی
یک فضای اندازهپذیر مثل را در نظر بگیرید که اندازه در آن تعریف شده است. مقادیر این اندازه، اعداد حقیقی مثبت بوده و البته متناهی است. در این حالت اگر مجموعه را عضوی از میدان سیگمایی در نظر بگیریم، خواهیم داشت:
با توجه به توضیحات گفته شده، اندازه را در فضای ، یک اندازه سیگما-متناهی () مینامند، اگر هر کدام از شرایط زیر برقرار باشند.
- اگر مجموعه توسط تعداد شمارشپذیر از مجموعههای شمارشپذیر با اندازه متناهی، پوشش (Covered) داده شود. بنابراین اگر مجموعه اعداد طبیعی (Natural Numbers) بوده و اگر که در آنها هستند، داریم:
- اگر مجموعه را بتوان بواسطه تعداد شمارشپذیر مجموعههای اندازهپذیر جدا از هم (Disjoint) پوشش داد. بدیهی است که اندازه هر یک از این مجموعهها نیز باید متناهی باشند. بنابراین اگر این مجموعههای جدا از هم را با مشخص کنیم، داریم:
- اگر مجموعه را بتوان بواسطه دنبالهای یکنوا (Monotone Sequence) به صورت صعودی یا نزولی و شمارشپذیر از مجموعههای با اندازه متناهی اندازهپذیر پوشش داد. بنابراین اگر با ویژگی باشند که برای هر یک از آنها ، آنگاه .
- اگر تابعی مثبت و انتگرالپذیر و اندازهپذیری مثل روی اندازه وجود داشته باشد. به این معنی که تابع در رابطه زیر صدق کند.
در این حالت با فرض آن که اندازه مورد نظر، مثلا یک اندازه سیگما-متناهی باشد، فضای اندازه را یک فضای اندازه سیگما-متناهی () مینامند.
«اندازه شمارشی» (Counting Measure) و «اندازه لبگ» (Lebesgue Measure) جزء گروه اندازههای سیگما-متناهی به ترتیب در فضای اعداد طبیعی و حقیقی هستند.
نکته: توجه داشته باشید که اندازه لبگ در فضای اعداد حقیقی، متناهی نیست ولی سیگما-متناهی خواهد بود. به این معنی که برای بعضی از فاصلهها یا مجموعههایی از اعداد حقیقی، اندازه لبگ که فاصله بین دو نقطه را مشخص میکند، ممکن است نامتناهی باشد ولی در عین حال میتوان هر اندازه لبگ برای یک فاصلهای از اعداد حقیقی را به صورت مجموع شمارشپذیر از اندازههای متناهی نوشت.

معرفی اندازه علامت دار
یک تعمیم روی اندازه (Measure) در نظریه اندازه، «اندازه علامتدار» (Signed Measure) است. از آنجایی در نظریه اندازه، مقادیر منفی جایی ندارند، اندازه علامتدار برای تعمیم مفهوم اندازه به کار رفت. یکی از کاربردهای جالب اندازه علامتدار در «قضیه تفکیک هان» (Hahn Decomposition Theorem) و «قضیه تفکیک جردن» (Jordan Decomposition Theorem) نهفته است که مشخص میکند که هر اندازه علامتدار را میتوان به دو اندازه عادی تفکیک کرد.
فضای اندازهپذیر را در نظر بگیرید که در ان یک مجموعه با میدان سیگمایی است. به این ترتیب همه مجموعههایی که در ادامه مورد بحث قرار میگیرند متعلق به هستند.
معمولا اندازه علامتدار را «متناهی» (Finite) در نظر میگیرند به این معنی که را یک اندازه علامتدار مینامند اگر دو مقدار و برایش مجاز نباشند. به مفهوم دقیقتر اگر مجموعه مقادیر اندازه علامتدار، مجموعه اعداد حقیقی باشد.
به همین ترتیب را «اندازه علامتدار تعمیم یافته» (Extended Signed Measure) مینامند اگر به شکل زیر معرفی شده و مجموعه مقادیر آن اعداد حقیقی تعمیم یافته (اعداد حقیقی به همراه و ) باشد.
در این صورت با شرط سیگما جمعپذیری (Sigma Additive) و مشخص بودن برای اندازه خواهیم داشت:
به شرطی که سری سمت راست در تساوی بالا، «مطلقا همگرا» (Converge Absolutely) بوده و ها دنبالهای از مجموعههای جدا از هم در باشند.

معرفی اندازه مطلقا پیوسته
در حسابان، خاصیت «پیوستگی مطلق» (Absolute Continuity)، نشانگر همواری منحنی تابع است که از «پیوستگی» (Continuity) و «پیوستگی یکنواخت» (Uniform Continuity)، شرط قویتری است. به این معنی که میتوان هر تابع مطلقا پیوسته را پیوسته یا پیوسته یکنواخت نامیده ولی اگر تابع پیوسته یا پیوسته یکنواخت باشد، دلیلی بر مطلقا پیوستگی آن وجود ندارد.
در این بحث، پیوستگی تابع به صورت یکنواخت و بدون پرش بودن تابع هنگام تغییرات روی متغیر یعنی در نظر گرفته میشود. به این ترتیب تابع روی مقادیر دامنهاش که مجموعه مقادیر را تشکیل میدهد، پیوسته است. همین امر هم در مورد اندازهها مورد بررسی قرار میگیرد و پیوستگی یک اندازه براساس اندازه دیگر، شرط پیوسته بودن اندازه خواهد بود.
ابتدا براساس بحث حد توابع، موضوع مطلقا پیوستگی را مورد بررسی قرار داده، سپس گزارههای معادل با آن را میآوریم.
تعریف و برای مطلقا پیوستگی تابع
در این قسمت را یک تابع روی یک بازه مثل در نظر گرفته که برد آن اعداد حقیقی است. پس در این حالت مینویسیم:
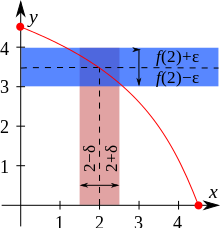
آنگاه تابع را روی ، مطلقا پیوسته گویند اگر مثبتی وجود داشته باشد که برای هر دنبالهای از زیرفاصلههای مجزا مانند از رابطه زیر برقرار باشد.
معمولا برای نمایش مطلقا پیوستگی تابع روی بازه از عبارت استفاده میشود. با توجه به تعریف ارائه شده، گزارههای زیر برای تابع مطلقا پیوسته، معادل هستند.
- تابع مطلقا پیوسته است.
- تابع تقریبا همهجا (Almost everywhere) مشتقپذیر با مشتق است بطوری که:
- تابعی انتگرالپذیر روی بازه وجود دارد که با شرط رابطه زیر تقریبا همه جا برقرار است.
نکته: رابطه اول و سوم در کنار یکدیگر، «قضیه اساسی مشتق و انتگرال لبگ در حسابان» (Fundamental Theorem of Lebesgue Integral Calculus) را تشکیل میدهد.
تعریف مطلقا پیوستگی اندازه
دو اندازه و را در یک فضای اندازهپذیر در نظر بگیرید. اندازه را نسبت به ، مطلقا پیوسته گویند اگر هر یک از رابطههای زیر برقرار باشد:
- اگر آنگاه برای هر . در این حالت مینویسیم:
- برای هر ، وجود دارد که به ازای آنها نتیجه میدهد .
نکته: گاهی مطلقا پیوستگی را با اصطلاح «تحت تسلط بودن» (Dominated) نیز به کار میبرند و مثلا میگویند که اندازه تحت تسلط اندازه است.
معرفی اندازههای منفرد
در ریاضیات، دو اندازه (اندازه علامتدار یا مختلط) مثل و که روی یک فضای اندازهپذیر مثل تعریف شدهاند را منفرد گوییم اگر دو مجموعه جدا از هم مثل و در وجود داشته باشد که اجتماع آنها کل را ساخته و اندازه برای تمام زیرمجموعههای صفر و اندازه روی تمام زیرمجموعههای نیز صفر باشد. در این صورت دو اندازه و را نسبت به یکدیگر «منفرد» (Singular) مینامند.
نکته: با توجه به اینکه و افرازی از هستند، داریم:
قضیه تفکیک لبگ اندازه علامتدار سیگما-متناهی
همانطور که اشاره شد، قضیه تفکیک لبگ در نظریه اندازه، مرتبط با دو اندازه علامتدار و سیگما متناهی () است که نشان میدهد قابلیت تفکیک چنین اندازههایی به دو اندازه با همین خصوصیات وجود دارد. بنابراین اگر را یک فضای اندازهپذیر و و را دو اندازه علامتدار سیگما-متناهی در نظر بگیریم، میتوان دو اندازه مثل و پیدا کرد که در روابط زیر صدق کنند.
- میتوان اندازه را به صورت مجموعه دو اندازه علامتدار و سیگما متناهی نوشت:
یکی از اندازههای علامتدار و سیگما-متناهی (مثلا ) نسبت به مطلقا پیوسته (Absolute Continuous) است یا تحت تسلط است.
- اندازه علامتدار دیگر (مثلا ) نسبت به ، منفرد (Singular) است.
نکته: این دو اندازه یعنی و به طور منحصر به فردی توسط دو اندازه و قابل تعیین هستند.
تعمیم قضیه تفکیک لبگ
قضیه تفکیک لبگ را میتوان به صورتهای گوناگونی تعمیم داد. ابتدا برای اندازههای تعریف شده در مجموعههای بورل روی اعداد حقیقی به بحث میپردازیم.
فرض کنید یک اندازه بورل باشد که میدانیم تحت اندازه لبگ () مطلقا پیوسته است. آنگاه رابطه زیر که نشانگر تفکیک اندازه است، برقرار خواهد بود:
بطوری که هر یک از این اندازهها به صورت زیر تعریف میشوند.
- یک اندازه مطلقا پیوسته تحت اندازه لبگ باشد.
- مربوط به بخش اندازه منفرد پیوسته اندازه است.
- همینطور هم قسمت «نقاط خالص» (Pure Point) یا «اندازه گسسته» (Discrete Measure) است که در تک نقطههای بورل، دارای مقدار است.
تفکیک لوی ایتو
براساس ارتباط بین اندازه احتمال و نظریه اندازه، یک فرآیند تصادفی را به کمک «تفکیک لوی-ایتو» (Lévy–Itō decomposition) میتوان به صورت بخشهای مجزا نشان داد. فرض کنید فرآیند یک «فرایند لوی» (Levy Process) باشد. آنگاه چنین فرآیندی را میتوان به صورت سه فرایند لوی مستقل دیگر به صورت زیر نشان داد.
که هر یک از آنها به صورت زیر تعریف میشوند.
- یک «حرکت براونی» (Brownian Motion) است که مترادف با بخش مطلقا پیوسته در تفکیک لبگ خواهد بود.
- یک «فرآیند پواسن ترکیبی» (Compound Poisson Process) است که مترادف با بخش نقاط خالص در تفکیک لبگ در نظر گرفته میشود.
- نیز یک «مارتینگل» (Martingale) است که دارای تعداد نقاط پرش شمارش پذیر در یک فاصله متناهی است که مترادف با بخش منفرد در قضیه تفکیک لبگ محسوب میشود.
خلاصه و جمعبندی
در این نوشتار به بررسی قضیه تفکیک لبگ پرداختیم و البته نکاتی که برای فهم درست و بهتر آن لازم بود نیز در متن مورد اشاره قرار گرفت. اندازه علامتدار، اندازه سیگما-متناهی نیز در این متن مورد بررسی و تجزیه و تحلیل شدند. همچنین «قضیه تفکیک لوی-ایتو» (Lévy–Itō decomposition) نیز که یک تعمیم روی قضیه تفکیک لبگ است، از محتویات این متن محسوب میشود.
اگر مطلب بالا برایتان مفید بوده است، آموزشها و نوشتارهای دیگر مجله فرادرس که در ادامه قابل مشاهده هستند، نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش مبانی آنالیز حقیقی
- مجموعه آموزشهای آمار و احتمالات
- آموزش توابع مختلط (Complex Functions)
- فضای متریک و نامساوی مثلثی — به زبان ساده
- تجزیه هان و کاربردهای آن — به زبان ساده
- قضیه مقدار میانی (Intermediate Value Theorem) — به زبان ساده
^^