طیف اتمی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

احتمالا تاکنون شنیدهاید که خورشید از هِلیم تشکیل شده یا اینکه جنس یکی از قمرهای مشتری از متان است. بدیهی است که تاکنون بشر نتوانسته به سطح خورشید یا سطح اروپا (قمر مشتری) سفر کند. بنابراین دانشمندان به چه صورت جنس این اجرام را شناسایی میکنند؟ پاسخ در «طیف اتمی» (Atomic Spectrum) عناصر است. طیف اتمی، مفهومی است که ترکیب تشیکل دهنده یک ماده یا هر جرمی را میتوان با استفاده از آن تعیین کرد. در این مطلب قصد داریم تا این مفهوم را شرح دهیم. توجه داشته باشید که پیش از مطالعه این مطلب بایستی با مفاهیم عدد اتمی و جرمی آشنا باشید.
فیلم آموزشی طیف اتمی
مقدمه
انرژی میتواند در خلاء یا محیطی مادی، در قالب امواج الکترومغناطیسی منتشر شود. تابش الکترومغناطیسی، موجی عرضی است که در آن دو میدان الکتریکی و مغناطیسی به صورت عمود به یکدیگر و به شکل نوسانی در محیط حرکت میکنند.
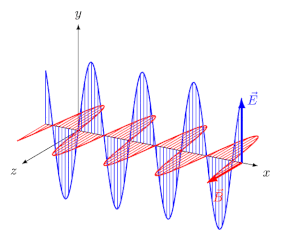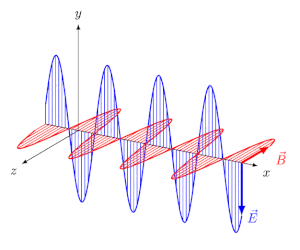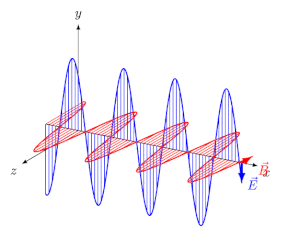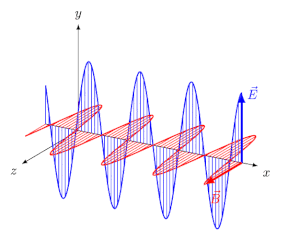
در انیمیشن فوق نیز میبینید که دو میدان الکتریکی و مغناطیسی عمود به یکدیگر در راستای x در حال حرکت هستند. فاصله دو قله از موج را طول موج مینامند. در شکل زیر طول موج، نشان داده شده است.
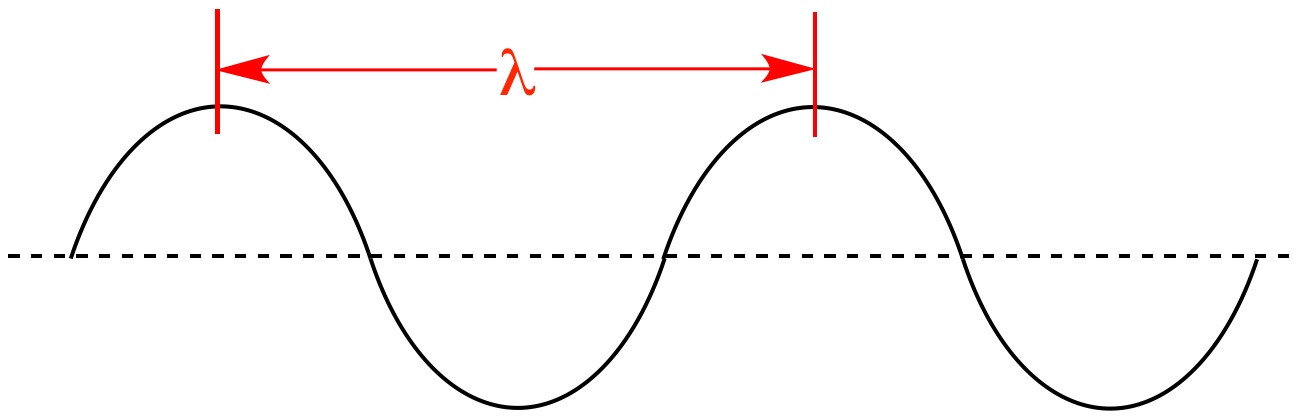
بدیهی است که هرچه طول موج کمتر باشد، موج فشردهتر شده و انرژی بیشتری را حمل میکند. طول موج دقیقا همان عاملی است که نورهای با رنگهای مختلف را از هم متمایز میکند. البته فرکانس نیز کمیتی است که میتوان با استفاده از آن میزان فشردگی یک موج را بیان کرد. در حقیقت فرکانس و طول موج با عکس هم در ارتباط هستند. طیف الکترومغناطیسی به بازهای از تمامی طول موجها و فرکانسهای ممکن گفته میشود که در آن موج الکترومغناطیسی میتواند منتشر شود.
طبق توصیف کوانتوم مکانیک از الکترون، که مفهوم «دوگانگی موج-ذره» (Wave-Particle Duality) را بیان میکند، اگرچه پدیده الکترومغناطیس در نور را تحت عنوان موج میشناسند، اما در مواردی به این پدیده همچون ذره نیز نگاه میشود.
ماکس پلانک، فیزیکدان آلمانی، در سال ۱۹۰۰ در هنگام مطالعه تابش جسم سیاه، متوجه این موضوع شد که با افزایش پیوسته فرکانس یک موج، انرژی تابشی بدست آمده از منبع تابش، بهصورت پیوسته افزایش نمییابد. در حقیقت افزایش انرژی بهصورت پلهای یا اصطلاحا کوانتومی رخ میدهد. بهعبارت دیگر یک بستهی انرژی از سیستم همانند یک اتم از یک جرم است.
آلبرت انیشتین، در سال ۱۹۰۵ مقالهای ارائه داد که در آن نور را بهصورت بستههایی از انرژی تحت عنوان فوتون در نظر گرفت. او با استفاده از توصیفش از نور، پدیدهای تحت عنوان اثر فوتوالکتریک را نیز شرح داد. کشف فوتون، افزایش پلهای (یا افزایش کوانتومی) انرژی تابشی را توجیه کرد.
ثابتها و واحدها
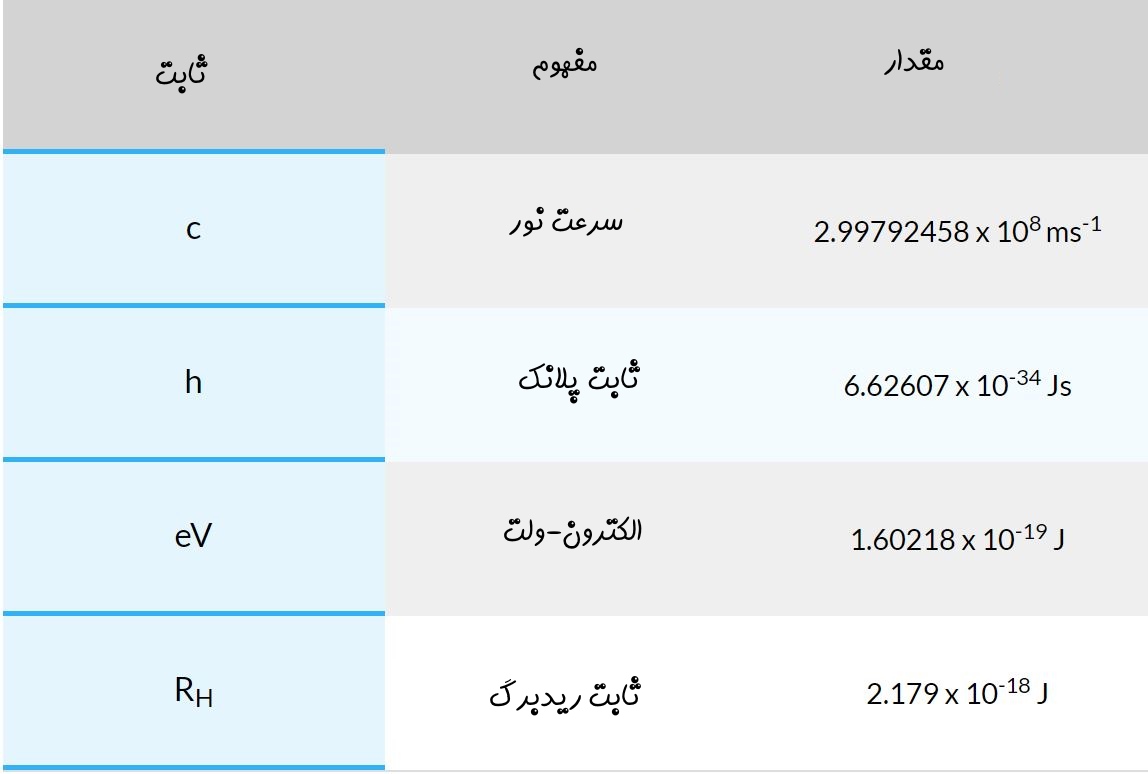
ثابتهای استفاده شده در این مطلب به شرح زیر هستند:
- : طول موج نور
- : فرکانس نور
- n: عدد کوانتومیِ سطح انرژی
- E: سطح انرژی
همچنین در جدول زیر نمادهای استفاده شده و مقدار آنها نیز ارائه شدهاند.
واحدها
طول موج یا فاصلهی بین دو قلهی یک موج معمولا بر حسب متر بیان میشود. البته بهدلیل کوچک بودن این کمیت در مواردی آن را بر حسب دیگر واحدها همچون میکرومتر یا نانومتر نیز بیان میکنند. تعداد قلههایی از موج که در ۱ ثانیه عبور میکند نیز فرکانس موج نامیده میشود.
واحد SI فرکانس موج هرتز است که معمولا آن را با نماد Hz نمایش میدهند. فرکانس بر حسب بیان میشود. سرعت نور در خلاء نیز عددی ثابت و برابر با در نظر گرفته میشود. رابطه بین سرعت نور، طول موج و فرکانس بهشکل زیر است.
انرژی تابش الکترومغناطیسی در یک فرکانس مشخص نیز بهصورت ژول بیان شده و از رابطه زیر بدست میآید.
در رابطه فوق h ثابت پلانک نامیده شده و مقدار آن برابر با است. رابطه فوق انرژی حمل شده توسط یک بستهی کوانتومی (یک فوتون) را نشان میدهد. بنابراین مقدار این انرژی بسیار اندک است. لذا از واحد دیگری تحت عنوان الکترون ولت نیز استفاده میشود.
۱ الکترون-ولت به مقداری از انرژی جنبشی اطلاق میشود که الکترون در نتیجهی شتاب گرفتن در اختلاف پتانسیل ۱ ولت بدست میآورد. در حقیقت ۱ الکترون-ولت برابر است با:
طیفسنجی
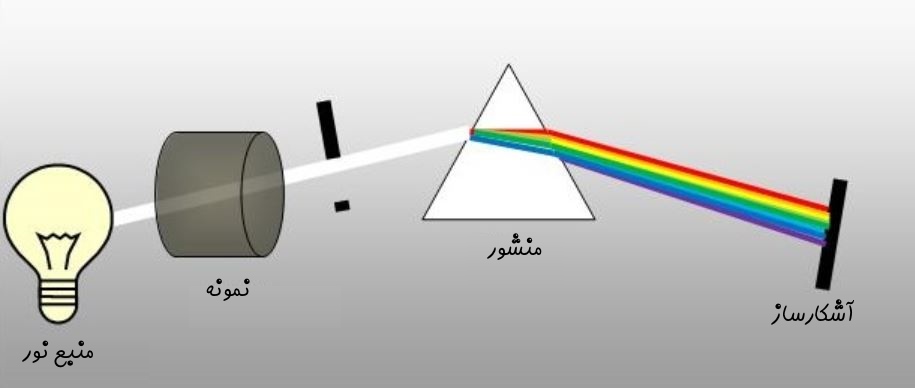
همانگونه که در فوق نیز عنوان شد، یک طیف به بازهای از فرکانسها و طول موجها گفته میشود. با عبور دادن نور از داخل منشور میتوان آن را به بخشهایی با طیفهای مشخص تقسیم کرد. اگرچه این روش بسیار مبتدیانه، اما کارآمد.
به روش فوق، طیف سنجی یا «اسپکتروسکوپی» (Spectroscopy) گفته میشود. در شکل زیر نحوه شکست نور به نورهایی با طیفهای مختلف نشان داده شده است.
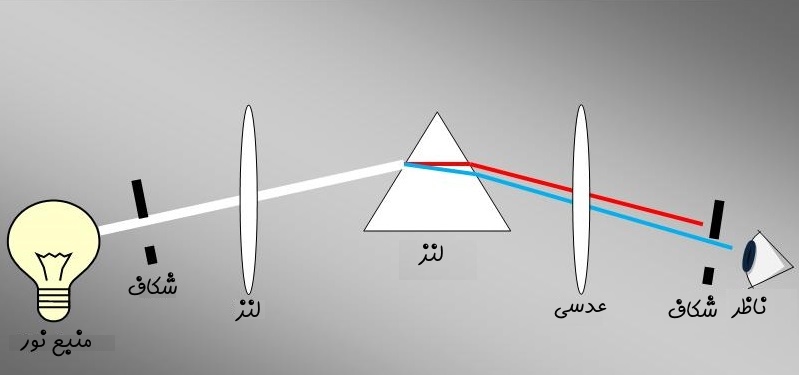
در شکل بالا نور با استفاده از یک عدسی متمرکز شده و به داخل منشور فرستاده شده است. پس از آن شکسته شده و به چشم ناظر میرسد. در حقیقت با استفاده از همین تحلیل است که میتوان فهمید سطح خورشید از هلیوم تشکیل شده. طیفسنجهای مدرن امروزی نیز مبتنی بر همین اصل کار میکنند.
واکنش اتمها به تابش نور
همانطور که در مبحث اوربیتال نیز عنوان شد، الکترونها تنها میتوانند در ناحیه مشخصی تحت عنوان پوسته در اطراف اتم قرار گیرند. هر پوسته دارای سطحی از انرژی است که با استفاده از عدد n نشان داده میشود. با توجه به این که الکترون نمیتواند بین سطوح انرژیِ مشخص شده قرار گیرد، بنابراین عدد n نیز دارای مقداری مثبت و حقیقی است (...,n=1,2,3).
نزدیکترین الکترون به هستهی اتم دارای n=1 بوده و همچنین کمترین انرژی را دارد. اصطلاحا گفته میشود که این الکترون در حالت پایه (Ground State) قرار گرفته است. انرژی الکترونی که در سطح انرژی n قرار گرفته با استفاده از رابطهی زیر توصیف میشود.
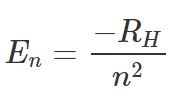
در رابطه فوق، ثابتی است که مقدار آن برابر با بوده و n نشان دهنده سطح انرژی الکترون است. در شکل ۱ زیر الکترون، پوسته و فرآیند دفع و جذب انرژی نوری نشان داده شده است.
زمانی که نوری به یک اتم تابیده شود، الکترونهای آن، فوتون دریافت کرده و در نتیجه سطح انرژی آنها تغییر کرده و به لایههای دورتر میروند. هرچه انرژی دریافت شده توسط الکترون بیشتر باشد، تغییر سطح الکترون به لایههای دورتر نیز بیشتر خواهد بود.
بهطور مشابه یک الکترون میتواند با از دست دادن فوتون، انرژی از دست داده و به سطوح پایینتر تغییر سطح دهد. تغییر سطح انرژی الکترون در نتیجه از دست دادن یا گرفتن فوتون برای اولین بار در قالب مدل اتمی بور ارائه شد. انرژی گرفته شده یا از دست داده شده توسط الکترون هنگامی که تغییر سطح میدهد، برابر است با:
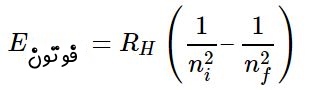
در رابطه فوق سطح انرژی اولیه الکترون و سطح انرژی نهایی الکترون را نشان میدهد. فرکانس فوتونی که منجر به تغییر سطح الکترون میشود را میتوان با استفاده از رابطهی بدست آورد. در رابطه فوق انرژی اولیه الکترون و انرژی نهایی آن است. در شکل زیر الکترون، هسته، پوسته و فرآیند دفع و جذب فوتون توسط الکترون، نشان داده شده است.
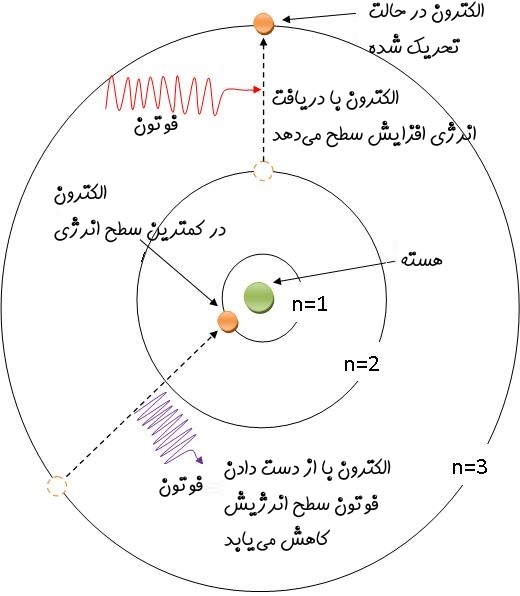
با توجه به اینکه یک الکترون میتواند در سطح خاصی از انرژی قرار داشته باشد، بنابراین میتواند فوتونها را در طیف خاصی منتشر کند. به همین دلیل است که خطوط طیفی بوجود میآیند.
خطوط نشر
همانطور که در بالا نیز عنوان شد، زمانی که الکترونی از سطح انرژی بالایی به سطح انرژی پایینتری جابجا شود، از خود فوتونی با طول موج و فرکانس خاصی نشر میدهد. زمانی که مجموعهای از الکترونها، فوتونهایی با طول موج یکسان را نشر دهند، مجموعهای از خطوط با همین طول موج ایجاد میشود. شکل زیر را در نظر بگیرید.
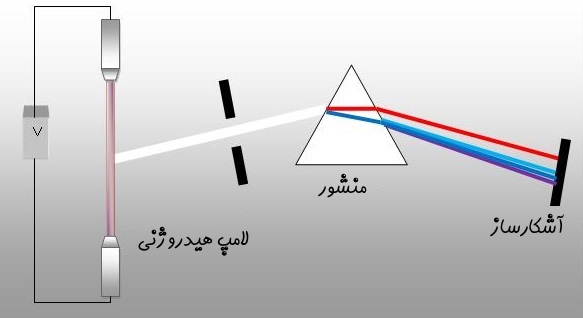
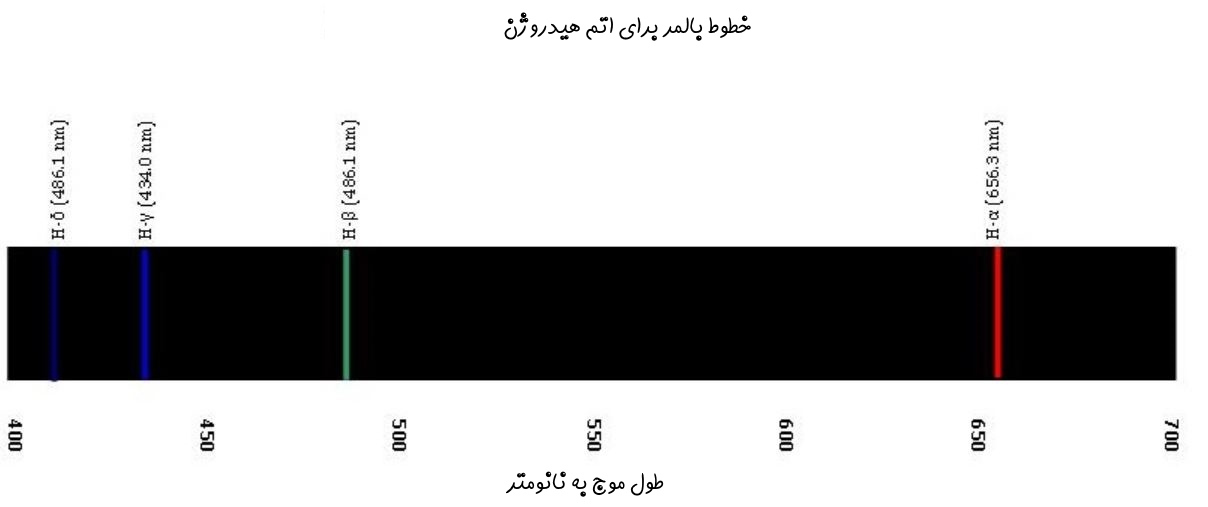
در سمت چپ لامپی هیدروژنی قرار گرفته که توسط جریان الکتریکی تحریک میشود. در مرحلهی بعد نورِ ناشی از تحریک، از منشور عبور داده میشود و در نتیجه به نورهایی با فرکانسهای متفاوت تقسیم میشود. از آنجایی که فرکانسهای نور، مرتبط با سطوح انرژی متفاوت هستند، میتوان خطوط طیفی اتم هیدروژن را با استفاده از معادله کشف شده توسط «یوهان بالمِر» (Johann Balmer) بدست آورد. این معادله در زیر بیان شده است.
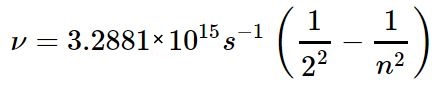
در این رابطه، n عددی بزرگتر از ۲ است. دلیل این امر صادق بودن رابطه فوق برای نور مرئی و برخی از فرکانسهای فرابنفش است. شکل زیر خطوط بالمر برای اتم هیدروژن را نشان میدهد.
خطوط جذب
زمانیکه یک الکترون از سطح انرژی پایین به سطح انرژی بالاتر حرکت میکند، فوتونی با طول موجی خاص را جذب میکند. این امر باعث میشود طیفهای مربوط به فوتون جذب شده به رنگ مشکی در آید. برای درک بهتر به شکل زیر توجه فرمایید.
همانگونه که در شکل فوق میبینید در ابتدا نوری از یک نمونه ماده عبور داده شده است. الکترونهای ماده فوتونهای مربوط به طیف جذب را از نور دریافت کرده و افزایش انرژی میدهند. در نتیجه پس از عبور دادن نور از منشور طیف مذکور شناسایی نشده و به رنگ سیاه در میآید.
کاربردهای طیف اتمی
طیف اتمی کاربردهای عملی بسیاری دارد. در حقیقت با توجه به اینکه فرکانس نشر برای هر عنصر متفاوت است، بنابراین این ویژگی همچون اثر انگشت برای اتمها عمل میکند. برخی از اتمها با استفاده از تحلیل طیف اتمی کشف شدند. برای نمونه دانشمندان با مادهای جدید برخوردند که طیف اتمی متفاوتی داشت.
آنها با استفاده از تحلیل طیف اتمی متوجه شدند با مادهای جدید روبرو شدند. بعدها این عنصر هلیوم نامگذاری شد. همچنین ستارهشناسان با استفاده از مفهوم طیفی اتمی میتوانند جنس اجرام دوردست را پیشبینی کنند. در ادامه جهت درک بهتر مفاهیم کمی بیان شده، مثالهایی مطرح شده است.
مثال ۱
با استفاده از معادله بالمر فرکانس تابشی مربوط به سطح انرژی n=3 را بیابید.
در بالا معادله بالمر را بهصورت بیان کردیم. با جایگذاری n=3 در رابطه فوق داریم:
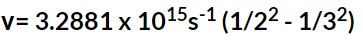
در نتیجه مقدار بدست میآید.
مثال ۲
فرکانس نور تابش شده در حالتی که الکترونی از n=5 به سطح انرژی n=2 نزول میکند، چقدر است؟
جهت بدست آوردن فرکانس نور تابیده شده از رابطه استفاده میکنیم. در نتیجه انرژی ساطع شده در نتیجه این پرش سطح انرژی برابر است با:
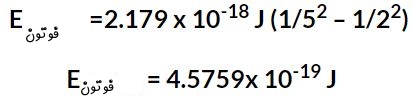
حال با استفاده از رابطه مقدار فرکانس نور ساطع شده برابر است با:
در صورت علاقهمندی به مباحث مرتبط در زمینه فیزیک و شیمی آموزشهای زیر نیز به شما پیشنهاد میشوند:













خیلی عالی بود ،ممنون بابت زحماتتون?
سلام
چرا مدل اتمی بور نمی تواند متفاوت بودن شدت خط های طیف گسیلی را توضیح دهد و منشاء تفاوت شدت خط های طیف گسیلی چیست ؟ (برای مثال مدل بور نمی تواند توضیح دهد که چرا شدت خط قرمز با شدت خط آبی در طیف گسیلی هیدروژن با یکدیگر متفاوت است.)
با سلام،
شدت خطوط طیف اتمی به تعداد فوتونهای با فرکانس یا طول موج یکسان که جذب یا منتشر شدهاند بستگی دارد. به این نکته توجه داشته باشید که در مدل اتمی بور از برهمکنشهای بین الکترونها داخل اتم صرفنظر شده است. بنابراین، بسیاری از ویژگیهای پیچیده اتم توسط این مدل توضیح داده نمیشود.
با تشکر از همراهی شما با مجله فرادرس
The brightness or intensity of spectral lines depends upon the number of photons of same frequency or wavelength emitted or absorbed.
عالی بود???
سلام و تشکر فراوان از آموزشتون
واقعا عالی بود من تمام سوالات که تو ذهنم بود در رابطه با نور بود رو گرفتم
ممنون از زحمات
سلام
سپاس بابت مطلب مفید شما