درون یابی چند جمله ای — به زبان ساده

گاهی لازم است مقدار تابع $$y = f ( x )$$ را در یک نقطه معین $$x$$، بر اساس مقادیر معلوم $$f ( x _ 0 )$$، ... و $$f ( x _ n )$$ در مجموعه $$n + 1$$ نقطه $$a = x _ 0 \le x _ 1 \le \cdots \le x _ n = b$$ در بازه $$[a , b ]$$ تخمین بزنیم. اگر $$a < x < b$$ باشد، این فرایند «درون‌یابی» (Interpolation) نامیده می‌شود و اگر $$x < a$$ یا $$x > b$$ باشد، به آن «برون‌یابی» (Extrapolation) می‌گوییم. در این آموزش، با «درون یابی چند جمله ای» (Polynomial Interpolation) آشنا می‌شویم.

درون یابی چند جمله ای

یکی از راه‌های انجام درون‌یابی و برون‌یابی، تقریب تابع $$f ( x )$$ با یک چندجمله‌ای مرتبه $$n$$اُم است:

$$\large \begin {equation} f ( x ) \approx P _ n ( x ) = a _ n x ^ n + a _ { n - 1 } x ^ { n - 1 } + \cdots + a _ 2 x ^ 2 + a _ 1 x + a _ 0 = \sum _ { j = 0 } ^ n a _ j x ^ j \end {equation}$$

فیلم آموزش محاسبات عددی – مرور و حل مساله در فرادرس

کلیک کنید

که در آن، $$n + 1$$ ضریب $$a _ 0$$، ... و $$a _ n$$ را می‌توان با $$n + 1$$ نقطه داده شده به دست آورد. وقتی $$P _ n ( x )$$ را به دست آوریم، می‌توانیم هر عملیاتی (مانند مشتق‌گیری، انتگرال‌گیری، یا یافتن ریشه) را که می‌خواهیم روی تابع $$f ( x )$$ انجام دهیم، آن را به صورت تقریب به $$P _ n ( x ) \approx f ( x )$$ اعمال کنیم. این کار، به ویژه در مواقعی که تابع $$f ( x )$$ یک تابع غیرمقدماتی بوده و در نتیجه، کار با آن دشوار باشد، یا فرم بسته‌ای نداشته باشد، بسیار کارساز خواهد بود.

به طور مشخص، برای یافتن ضرایب $$P _ n ( x )$$، لازم است همه نقاط $$\{ x _ i , y _ i = f ( x _ i ) , \; i = 0 , \cdots , n \}$$، یعنی $$n + 1$$ معادله خطی زیر را داشته باشیم:

$$\large \begin {equation} P _ n ( x _ i ) = \sum _ { j = 0 } ^ n a _ j x ^ j_ i = f ( x _ i ) = y _ i , \; \; \; \; ( i = 0 , \cdots , n ) \end {equation}$$

اکنون می‌توان ضرایب $$a _ 0$$، ... و $$a _ n$$ را با حل این $$n + 1$$ معادله خطی به دست آورد. این معادلات را می‌توان به فرمی ماتریسی زیر نوشت:

$$\large \begin {equation} \left [ \begin {array} {ccccc} 1 & x _ 0 & x _ 0 ^ 2 & \cdots & x _ 0 ^ n \\ 1 & x _ 1 & x _ 1 ^ 2 & \cdots & x _ 1 ^ n \\ 1 & x _ 2 & x _ 2 ^ 2 & \cdots & x _ 2 ^ n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x _ n & x _ n ^ 2 & \cdots & x _ n ^ n \end {array} \right ] \left [ \begin {array} { c } a _ 0 \\ a _ 1 \\ a _ 2 \\ \vdots \\ a _ n \end {array} \right] = { \bf V } { \bf a } = \left [ \begin {array} { c } y _ 0 \\ y _ 1 \\ y _ 2 \\ \vdots \\ y _ n \end {array} \right] = { \bf y } \end {equation}$$

که در آن، $${\bf a}=[a_0,\cdots,a_n]^T$$ و $${\bf y}=[y_0,\cdots,y_n]^T$$ و

$$\large \begin {equation} { \bf V } = \left [ \begin {array} {ccccc} 1 & x _ 0 & x _ 0 ^ 2 & \cdots & x _ 0 ^ n \\ 1 & x _ 1 & x _ 1 ^ 2 & \cdots & x _ 1 ^ n \\ 1 & x _ 2 & x _ 2 ^ 2 & \cdots & x _ 2 ^ n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x _ n & x _ n ^ 2 & \cdots & x _ n ^ n \end {array} \right ] \end {equation}$$

ماتریس $$\mathbf {V}$$ به عنوان «ماتریس وندرموند» (Vandermonde Matrix) شناخته می‌شود. با حل این دستگاه، ضرایب $$[a_0,\cdots,a_n]^T={\bf a}={\bf V}^{-1}{\bf y}$$ به دست می‌آیند. در اینجا، $$n +1$$ چندجمله‌ای $$x ^ 0$$، $$x ^ 1$$، $$x ^ 2$$، ... و $$x ^ n$$ را می‌توان به عنوان مجموعه‌ای از توابع پایه چندجمله‌ای در نظر گرفت که فضای همه چندجمله‌ای‌های درجه $$n$$اُم را اسپن می‌کنند. اگر نقاط $$x _ 0$$، ... و $$x _ n$$ متمایز باشند، یعنی $$\mathbf { V}$$ دارای رتبه کامل بوده و معکوس آن، $$\mathbf { V} ^ { - 1 }$$، وجود داشته باشد، آنگاه جواب سیستم $$\mathbf {a } = \mathbf { V} ^ {-1} \mathbf { f}$$ و در نتیجه $$P _ n ( x )$$ یکتا است.

البته در عمل این روش به دو دلیل استفاده نمی‌شود: اول اینکه پیچیدگی محاسباتی $$O ( n ^ 3 )$$ برای محاسبه معکوس $$\mathbf { V}$$ زیاد است و دوم اینکه با افزایش $$n$$ ماتریس $$\mathbf { V}$$ بدحالت‌تر می‌شود. بنابراین روش‌های دیگری نیز برای درون‌یابی پیشنهاد شده‌اند.

خطای درون یابی چند جمله ای این‌گونه تعریف می‌شود:

$$\large R _ n ( x ) = f ( x ) - P _ n ( x )$$

که در حالت کلی غیرصفر است، البته جز در نقطه $$x = x _ i$$ که $$R_n(x_i)=0,\;(i=0,\cdots,n)$$ است. به عبارت دیگر، تابع خطای $$R_ n ( x )$$ دارای $$n + 1$$ ریشه در $$x _ 0$$، ... و $$x _ n$$ است و در نتیجه، می‌توان آن را به صورت زیر نوشت:

$$\large R _ n ( x ) = u ( x ) \prod _ { i = 0 } ^ n ( x - x _ i ) =u ( x ) \omega ( x )$$

که در آن، $$u ( x )$$ یک تابع مجهول و $$\omega ( x )$$ یک چندجمله‌ای درجه $$n + 1$$ است که به صورت زیر تعریف می‌شود:

$$\large \omega ( x ) = \prod _ { i = 0 } ^ n ( x - x _ i )$$

برای یافتن $$u ( x )$$، تابع دیگری به نام $$F ( t )$$ از متغیر $$t$$ را تشکیل می‌دهیم که در آن، هر $$x \in ( a , b )$$ به عنوان یک پارامتر در نظر گرفته می‌شود:

$$\large F ( t ) = R _ n ( t ) - u ( x ) \prod _ { i = 0 } ^ n ( t - x _ i ) = f ( t ) - P _ n ( t ) - u ( x ) \prod _ { i = 0 } ^ n ( t - x _ i )$$

که در $$t = x$$ برابر با صفر است:

$$\large F ( x ) = R _ n ( x ) - u ( x ) \prod _ { i = 0 } ^ n ( x - x _ i ) = R _ n ( x ) - R _ n ( x ) = 0$$

بنابراین، می‌توان گفت که $$F ( t )$$ دارای $$n + 2$$ ریشه در $$x _ 0$$، ... و $$x _ n$$ و $$x$$ است. قضیه رول بیان می‌کند که تابع مشتق $$f' ( x )$$ هر تابع مشتق‌پذیر $$f ( x )$$ که در رابطه $$f ( a ) = f ( b ) = 0$$ صدق می‌کند، باید حداقل یک ریشه در $$c \in ( a , b )$$ داشته باشد. طبق «قضیه رول» (Rolle's Theorem)، $$F' ( t )$$ حداقل $$n + 1$$ ریشه بین دو ریشه متوالی $$F ( t)$$ دارد و $$F ^ {\prime \prime } ( t )$$ حداقل $$n$$ ریشه، و $$F ^ {( n + 1 ) } ( t)$$ حداقل یک ریشه در $$\xi\in(a,\;b)$$ دارد:

$$ \large \begin {eqnarray}<br /> F ^ { ( n + 1 ) } ( \xi ) = 0 & = & \frac { d ^ { n + 1 } } { d t ^ { n + 1 } }<br /> \left [ f ( t ) - P _ n ( t) - u ( x ) \prod _ { i = 0 } ^ n ( t -x _ i ) \right ] _ { t = \xi }<br /> \nonumber \\<br /> & = & \left [ f ^ { ( n + 1 ) } ( t ) + P _ n ^ { ( n + 1 ) } ( t ) - u ( x ) \frac { d ^ { n + 1 } } { d t ^ { n + 1 } } \prod _ { i = 0 } ^ n ( t - x _ i ) \right ] _ { t = \xi }<br /> \nonumber \\<br /> & = & f ^ { ( n + 1 ) } ( \xi ) - u ( x ) ( n + 1 ) !<br /> \end {eqnarray} $$

معادله آخر به این دلیل است که $$P _ n ( t)$$ و $$\prod_{i=0}^n(t-x_i)$$، به ترتیب، چندجمله‌ای‌هایی از درجه $$n$$ و $$n+1$$ از $$t$$ هستند. با حل معادله بالا، داریم:

$$\large u ( x ) = \frac { f ^ { (n + 1 ) } ( \xi ) } { ( n + 1 ) ! }$$

اکنون تابع خطا را می‌توان به صورت زیر نوشت:

$$\large R _ n ( x ) = u ( x ) \prod _ { i = 0 } ^ n ( x -x _ i ) = \frac { f ^ { ( n + 1 ) } ( \xi ) } {( n + 1 ) ! } \, \omega ( x )$$

که در آن، $$\xi ( x )$$ نقطه‌ای است که بسته به $$x$$، بین $$a = x _ 0$$ و $$b = x _  n$$ واقع شده است. خطا را می‌توان به صورت کمّی و توسط نُرم دو $$R  _ n ( x )$$ اندازه‌گیری کرد:

$$\large \begin {equation} \epsilon = | | R _ n ( x ) | | _ 2 = \left ( \int _ a ^ b R ^ 2 _ n ( x ) \, d x \right ) ^ { 1 / 2 } \end {equation}$$

در عمل، اگر $$f ( x )$$ یک چندجمله‌ای مرتبه $$k \le n$$ و در نتیجه $$f^ {(n+1)} ( x ) = 0$$ باشد، آنگاه می‌توان آن را با $$P _ n ( x )$$ رون‌یابی دقیق کرد. اما اگر $$k > n$$ باشد، درون‌یابی یک جمله خطای غیرصفر $$f ^ {(n + 1 ) } ( x ) = ( n + 1 ) !$$ دارد و جمله خطا به صورت زیر در خواهد آمد:

$$\large R _ n ( x ) = \frac { f ^ { ( n + 1 ) } ( \xi ) } { ( n + 1 ) ! } \, \omega ( x ) = \omega ( x )$$

به دلیل یکتایی درون یابی چند جمله ای ، تحلیل خطای بالا را می‌توان به همه روش‌های دیگر درون‌یابی، از قبیل لاگرانژ و نیوتن نیز اعمال کرد.

مثال درون یابی چند جمله ای

تابع $$y = f ( x ) = x \sin ( 2 x + \pi / 4 ) + 1$$ را با یک چندجمله‌ای $$P _ 3 ( x )$$ با درجه $$n = 3$$، طبق $$n + 1 = 4$$ نقطه زیر تقریب بزنید.

فیلم آموزش محاسبات عددی در پایتون Python در فرادرس

کلیک کنید

$$\large \begin {equation} \begin {array} { c | | c | c | c | c } \hline i & 0 & 1 & 2 & 3 \\ \hline \hline x _ i & - 1 & 0 & 1 & 2 \\ \hline y _ i= f ( x _ i ) & 1.937 & 1.000 & 1.349 & -0.995 \\\hline \end {array} \nonumber \\ \end {equation}$$

حل: ابتدا ماتریس وندرموند را به دست می‌آوریم:

$$\large \begin {equation} { \bf V } = \left [ \begin {array} { c c c c } 1 & x _ 0 & x _ 0 ^ 2 & x _ 0 ^ 3 \\ 1 & x _ 1 & x _ 1 ^ 2 & x _ 1 ^ 3 \\ 1 & x _ 2 & x _ 2 ^ 2 & x _ 2 ^ 3 \\ 1 & x _ 3 & x _ 3 ^ 2 & x _ 3 ^ 3 \end {array} \right] = \left [ \begin {array} { c c c c } 1 & -1 & 1 & -1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 9 \end {array} \right] \nonumber \\ \end {equation}$$

و ضرایب را محاسبه می‌کنیم:

$$\large \begin {equation} { \bf a } = { \bf V } ^ { - 1 } { \bf y } = { \bf V } ^ { - 1 } \left [ \begin {array} { r } f ( x _ 0 ) \\ f ( x _ 1 ) \\ f ( x _ 2 ) \\ f ( x _ 3 ) \end {array} \right ] = \left [ \begin {array} { c c c c } 1 & -1 & 1 & -1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 9 \end {array} \right ] \left [ \begin {array} { r } 1.937 \\ 1.000 \\ 1.349 \\ -0.995 \end {array} \right ] = \left [ \begin {array} { r } 1.000 \\ 0.369 \\ 0.643 \\ -0.663 \end {array} \right ] \nonumber \\ \end {equation}$$

و در نتیجه، چندجمله‌ای درون‌یاب به عنوان یک مجموع وزن‌دار از $$n + 1 = 4$$ تابع توانی به عنوان توابع پایه برای اسپن فضای چندجمله‌ای به دست می‌آید:

$$\large \begin {equation} P _ 3 ( x ) = \sum _ { j = 0 } ^ n a _ j x ^ j = 1 . 0 + 0 . 3 6 9 \; x + 0 . 6 4 3 \; x ^ 2 - 0 . 6 6 3 \; x ^ 3 \nonumber \\ \end {equation}$$

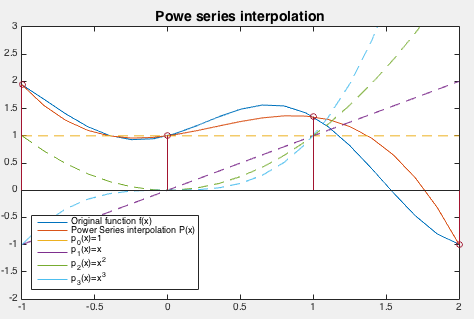
این چندجمله‌ای درون‌یاب $$P _ 3 ( x )$$ در شکل زیر نشان داده شده و با تابع اصلی $$f ( x )$$ مقایسه شده است. خطای $$\epsilon$$ را می‌توان با یک مجموعه از $$k >> n$$ نمونه گسسته $$u _ 1$$، ... و $$u _ k$$ از تابع $$f ( x )$$ و چندجمله‌ای درون‌یاب $$P _ 3 ( x )$$ تقریب زد:

$$\large \begin {equation} \epsilon = | | R _ 3 (x )| | _ 2 = \left ( \int _ a ^ b R ^ 2 _ 3 ( x ) \, d x \right ) ^ { 1 / 2 } \approx \left ( \frac { 1 } { k } \sum _ { i = 1 } ^ k [ f (u _ i ) - P _ 3 ( u _ i ) ] ^ 2 \right ) ^ { 1 / 2 } = 0 . 3 0 6 3 \nonumber \\ \end {equation}$$

پیاده‌سازی درون یابی چند جمله ای در متلب

کد متلب زیر، پیاده‌سازی روش درون یابی چند جمله ای را نشان می‌دهد.

فیلم آموزش محاسبات عددی با متلب MATLAB در فرادرس

کلیک کنید

1function [v P]=PI(u,x,y)  
2    % vectors x and y contain n+1 points and the corresponding function values
3    % vector u contains all discrete samples of the continuous argument of f(x)
4    n=length(x);     % number of interpolating points
5    k=length(u);     % number of discrete sample points
6    v=zeros(1,k);    % polynomial interpolation 
7    P=zeros(n,k);    % power function basis polynomials
8    V=zeros(n);      % Vandermonde matrix
9    for i=1:n
10        for j=1:n
11            V(i,j)=x(i)^(j-1);
12        end
13    end
14    c=inv(V)*y;      % coefficients
15    for i=1:n
16        P(i,:)=u.^(i-1);
17        v=v+c(i)*P(i,:);
18    end
19end

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های محاسبات عددی
• آموزش محاسبات عددی (مرور و حل مساله)
• مجموعه آموزش‌های دروس ریاضیات
• آموزش محاسبات عددی با MATLAB
• درون یابی اسپلاین — از صفر تا صد
• روش ژاکوبی — به زبان ساده
• برازش منحنی (Curve Fitting) — به زبان ساده

^^