چند جمله ای لاگرانژ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
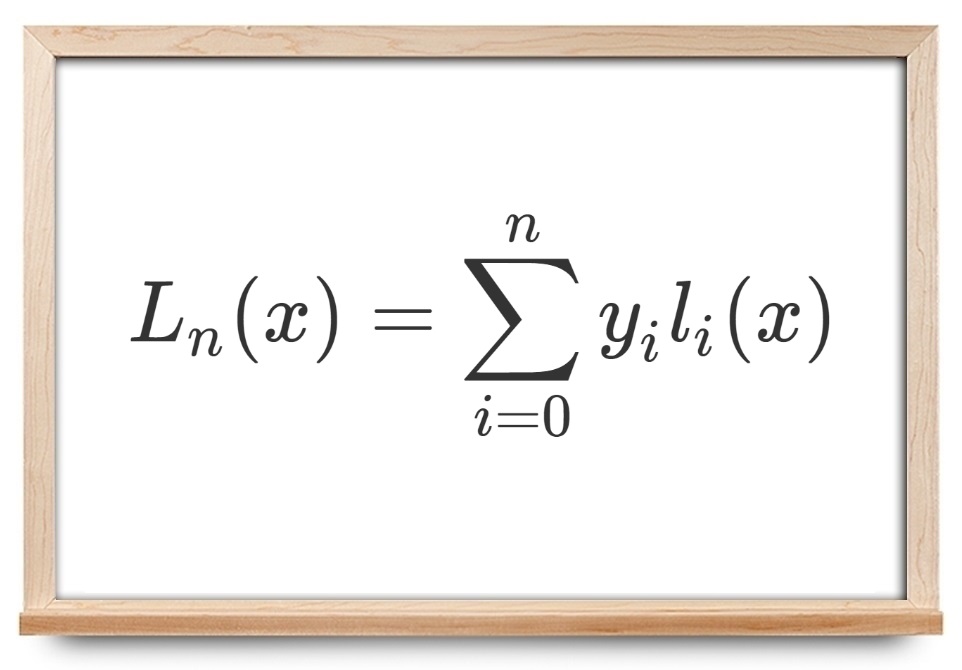
درونیابی روشی است که با استفاده از آن میتوان مقدار یک تابع را درون بازهای به دست آورد که مقدار دو نقطه ابتدا و انتهای آن بازه را میدانیم. در کاربردهای عملی، بسیار اتفاق میافتد که تعدادی نقطه داریم و میخواهیم مقدار بین آنها را به دست آوریم. در این مواقع، درونیابی بسیار کارساز خواهد بود. از درونیابی برای تقریب توابع پیچیده نیز میتوان استفاده کرد. روشهای متنوعی برای درونیابی پیشنهاد شده است که در این آموزش، درونیابی با چند جمله ای لاگرانژ (Lagrange Polynomial) را بررسی میکنیم.
تقریب چندجملهای
برای $$n$$ نقطه روی یک منحنی میتوان یک چندجملهای با درجه به اندازه کافی بزرگ از آنها عبور داد. یافتن این چندجملهایها اغلب برای افراد دشوار است.
برای مثال، سه نقطه $$ (1,1)$$ و $$ ( 2 , 2 ) $$ و $$ ( 3 , 2 ) $$ را در نظر بگیرید. برای یافتن چندجملهای $$ y = a_0 + a_1 x + a_2 x^2 $$ که از آنها میگذرد، به سادگی می توانیم این سه نقطه را در معادله چندجملهای قرار داده و به معادلات زیر برسیم:
$$ \large \begin {array} {c c l}
1 & = & a _ 0 + a _ 1 + a _ 2 \\
2 & = & a _ 0 + 2 a _ 1 + 4 a _ 2 \\
2 & = & a _ 0 + 3 a _ 1 + 9 a _ 2
\end {array} $$
و از این سه معادله، ضرایب را به دست آوریم. اگر معادلات را حل کنیم، $$ a _ 0 = - 1 $$، $$ a _ 1 = 2.5 $$ و $$ a _ 2 = -0.5 $$ را خواهیم داشت. به طریق مشابه، میتوانیم یک چندجملهای درجه $$n - 1 $$ را برای دقیقاً $$ n$$ نقطه به دست آوریم. اگر بیش از $$ n$$ نقطه داشته باشیم، میتوانیم از چندجملهای حداقل مربعات استفاده کنیم. البته، هدف ما این است که یک چندجملهای مرتبه $$ n- 1 $$ را برای $$n$$ نقطه به دست آوریم. در این آموزش، نشان میدهیم که چگونه میتوان با استفاده از چند جمله ای لاگرانژ این کار را انجام داد.
در حالی که کوچکترین چندجملهای که از $$ n$$ نقطه میگذرد از درجه $$ n - 1 $$ است، میتوان چندجملهای با مرتبه کوچکتری را نیز ارائه کرد. برای مثال، ممکن است یک سهمی (چندجملهای درجه دو) از چهار نقطه بگذرد.
قضیه زیر خلاصهای از آنچه است که به آن اشاره کردیم.
قضیه: فرض کنید $$ n $$ مقدار حقیقی $$ x _ 1$$، $$ x _ 2$$، ... و $$ x _ n $$ و $$n $$ مقدار حقیقی $$ y _ 1$$، $$ y_ 2$$، ... و $$ y_ n $$ داریم که لزوماً متمایز نیستند. یک چندجملهای $$P$$ با ضرایب حقیقی به گونهای وجود دارد که رابطه $$ P ( x _ i ) = y _ i $$ برای $$ i \in \{ 1 , 2 , ... , n \} $$ برقرار بوده و $$ \text{deg} ( P ) < n $$ است.
این قضیه را میتوان به عنوان این واقعیت نگریست که دو نقطه یک خط یکتا، سه نقطه یک چندجملهای مرتبه دوم یا سهمی یکتا، چهار نقطه یک چندجملهای مرتبه سوم یکتا و... را تعیین میکنند.
چند مثال ساده
با چند مثال ساده شروع کرده و فرمول چند جمله ای لاگرانژ را گام به گام بیان میکنیم.
فرض کنید نقطه $$ ( 1 , 3 ) $$ را داریم. چگونه میتوانیم یک چندجملهای پیدا کنیم که این نقطه را نمایش دهد؟ از آنجایی که درباره درجه چندجملهای چیزی گفته نشده، یک چندجملهای با کمترین درجه، یعنی درجه صفر را انتخاب میکنیم.
$$ \large \begin {align*} P ( x ) & = 3 \\ P ( 1 ) & = 3 \end {align*} $$
بنابراین، چندجملهای $$P ( x ) = 3 $$ نقطه مورد نظر را نمایش میدهد.
حال فرض کنید دو نقطه $$ ( 1 , 3 ) $$ و $$ ( 2 , 4 ) $$ را داشته باشیم. میخواهیم چندجملهای نمایش دهنده این دو نقطه را به دست آوریم. در اینجا، سادهترین چندجمله ای که دو نقطه در آن صدق کنند، درجه اول (یعنی یک خط راست) است:
$$ \large P ( x ) = \frac { ( x - 2 ) } { ( 1 - 2 ) } \times 3 + \frac { ( x - 1 ) } { (2 - 1 ) } \times 4 \\ \large \begin {align*}
P ( 1 ) & = 3 \\
P ( 2 ) & =4 \end {align*} $$
اکنون، سه نقطه $$ ( 1 , 3 )$$ و $$ ( 2 , 4 ) $$ و $$ ( 7 , 11 ) $$ را در نظر بگیرید. میخواهیم فرمولی برای چندجملهای که این سه نقطه در آن صدق میکنند، به دست آوریم. انتظار داریم یک سهمی این نقاط را تقریب بزند:
$$ \large P ( x ) = \frac { ( x - 2 ) ( x - 7 ) } { ( 1 - 2 ) ( 1 - 7 ) } \times 3 + \frac { ( x - 1 ) ( x - 7 ) } { ( 2 - 1 ) ( 2 - 7 ) } \times 4 + \frac { ( x - 1 ) ( x - 2 ) } { ( 7 - 1 ) ( 7 - 2 ) } \times 1 1 \\ \large \begin {align*} P ( 1 ) & = 3 \\ P ( 2 ) & = 4 \\ P ( 7 ) & = 11 \end {align*} $$
اگر به رابطه بالا دقت کنید، فرم عمومی آن به صورت زیر است:
$$ \large P ( x ) = \frac { \left ( x - x _ { 2 } \right ) \left ( x - x _ { 3 } \right) } { \left ( x _ { 1 } - x _ { 2 } \right ) \left ( x _ { 1 } - x _ { 3 } \right) } y _ { 1 } + \frac { \left( x - x _ { 1 } \right) \left( x - x _ { 3 } \right) } { \left( x _ { 2 } - x _ { 1 } \right) \left( x _ { 2 } - x _ { 3 } \right) } y _ { 2 } + \frac { \left( x - x _ { 1 } \right) \left( x - x _ { 2 } \right) } { \left( x _ { 3 } - x _ { 1 } \right) \left( x _ { 3 } - x _ { 2 } \right) } y _ { 3 } $$
یا به فرم مجموع، میتوان آن را اینگونه نوشت:
$$ \large P ( x ) = \sum _ 1 ^ 3 P _ i ( x ) y _ i $$
این، در حقیقت، همان فرمول چند جمله ای لاگرانژ برای درونیابی است که در ادامه، آن را به صورت کامل بیان میکنیم.
چند جمله ای لاگرانژ
فرض کنید $$ n$$ نقطه زیر داده شدهاند:
$$ \large ( x _ 1 , y _ 1 ) , ( x _ 1 , y _ 1 ) , ( x _ 2 , y _ 2 ) , . . . \ . .. ( x _ i , y _ i ) , . . . \ . . . ( x _ n , y _ n ) $$
و میخواهیم یک چندجملهای مرتبه $$n-1 $$ را به دست آوریم که این نقاط در آن صدق میکنند.
بدین منظور، تابع زیر را تعریف میکنیم:
$$ \large y = \sum _ { i = 1 } ^ n y _ i L _ i ( x ) $$
که همان چندجملهای مورد نظرمان است. در تابع بالا، $$ n$$ تابع $$ L_i(x)$$ را $$ n$$ چند جمله ای لاگرانژ مینامیم که چندجملهایهایی از درجه $$ n - 1 $$ هستند و به صورت زیر تعریف میشوند:
$$ \large L _ i ( x ) = \prod ^ n _ { j = 1 , \ j \neq i } \frac { x - x _ j } { x _ i - x _ j } $$
برای درک بهتر، سه چند جمله ای لاگرانژ نخست در زیر آورده شدهاند:
$$ \large L _ 1 ( x ) = \frac { ( x - x _ 2 ) ( x - x _ 3 ) ( x - x _ 4 ) . . . \ . . . ( x - x _ n ) } { ( x _ 1 - x _ 2 ) ( x _ 1 - x _ 3 ) ( x _ 1 - x _ 4 ) . . . \ . . . ( x _ 1 - x _ n ) } $$
$$ \large L _ 2 ( x ) = \frac { ( x - x _ 1 ) ( x - x _ 3 ) ( x - x _ 4 ) . . . \ . . . ( x - x _ n ) } { ( x _ 2 - x _ 1 ) ( x _ 2 - x _ 3 ) ( x _ 2 - x _ 4 ) . . . \ . . . ( x _ 2 - x _ n ) } $$
$$ \large L _ 3 ( x ) = \frac { ( x - x _ 1 ) ( x - x _ 2 ) ( x - x _ 4 ) . . . \ . . . ( x - x _ n ) } { ( x _ 3 - x _ 1 ) ( x _ 3 - x _ 2 ) ( x _ 3 - x _ 4 ) . . . \ . . . ( x _ 3 - x _ n ) } $$
در نگاه اول، فرمولهای بالا شاید کمی عجیب به نظر برسند، اما مثال عددی ساده مفهوم این فرمولها را سادهتر خواهد کرد.
مثال ۱
نقاط $$ ( 1 , 1 )$$، $$ ( 2 , 2 )$$ و $$ ( 3 , 2 ) $$ را در نظر بگیرید. سه چند جمله ای لاگرانژ به صورت زیر هستند:
$$ \large L _ 1 ( x ) = \frac { ( x - 2 ) ( x - 3 ) }{ (1 - 2 ) ( 1 - 3 ) } = \frac { 1 } { 2 } ( x ^ 2 - 5 x + 6 ) $$
$$ \large L _ 2 ( x ) = \frac { ( x - 1 ) ( x - 3 ) } { ( 2 - 1 ) ( 2 -3 ) } = - x ^ 2 + 4 x - 3 $$
$$ \large L _ 3 ( x ) = \frac { ( x - 1 ) ( x - 2 ) } { ( 3 - 1 ) ( 3 - 2 ) } = \frac { 1 } { 2 } ( x ^ 2 - 3 x + 2 ) . $$
با جایگذرای این چندجملهایها در تابع $$ y = \sum_{i=1}^n y_i L_i (x) $$، داریم:
$$ \large y = 1 \times \frac { 1 } { 2 } ( x ^ 2 - 5 x + 6 ) + 2 \times ( - x ^ 2 + 4 x - 3 ) + 2 \times \frac { 1 } { 2 } ( x ^ 2 - 3 x + 2 ) $$
که ساده شده آن به صورت زیر است:
$$ \large y = - \frac { 1 } { 2 } x ^ 2 + \frac { 5 } { 2 } x - 1 $$
همانطور که میبینیم، ضرایب این چندجملهای، با ضرایبی که در ابتدای این آموزش به دست آوردیم، همخوانی دارند.
درونیابی با چند جمله ای لاگرانژ
اگر چندجملهای گذرنده از $$ n $$ نقطه مورد نظر را به دست آوریم، میتوانیم از آن استفاده کرده و نقاط را درونیابی کنیم. بنابراین، میتوانیم ضرایب $$ y = a_0 + a_1 x^2 + a_2 x^2 ... $$ را با حل همزمان $$n$$ معادله به دست آوریم یا مستقیماً از معادله $$ y = \sum_{i=1}^n y_i L_i (x) $$ برای درونیابی (بدون نیاز به محاسبه ضرایب $$ a _ 0 $$، $$ a _ 1 $$ و...) استفاده کنیم که درونیابی لاگرانژ نام دارد. اگر تابع جدولبندی شدهای که میخواهیم یک مقدار درونیابی شده از آن به دست آوریم، یک چندجملهای با درجه کمتر از $$n$$ باشد، مقدار درونیابی شده دقیق خواهد بود. در غیر این صورت، این مقدار تقریبی است. یکی از مزایای درونیابی با چند جمله ای لاگرانژ نسبت به درونیابی بِسِلی، این است که لازم نیست تابعی را که باید درونیابی شود، در بازههای برابر $$x$$ جدولبندی کنیم. با این حال، اغلب توابع ریاضی و جداول نجومی در فواصل برابری جدولبندی میشوند و در این حالت میتوان از هر روشی استفاده کرد.
مثال ۲
مقدار $$ \sin 51^\circ $$ را با استفاده از جدول زیر تقریب بزنید:
$$ \large \begin {array} { r l }
x ^ \circ & \sin x \\
\\
0 & 0 . 0 \\
3 0 & 0 . 5 \\
6 0 & \sqrt { 3 } / 2 = 0 . 8 6 6 0 3 \\
9 0 & 1 . 0 \\
\end {array} $$
حل: مقدار چهار چند جمله ای لاگرانژ در $$ x = 51 $$ به صورت زیر است:
$$ \large L _ 1 ( 5 1 ) = \frac { ( 5 1 - 3 0 ) ( 5 1 - 6 0 ) ( 5 1 - 9 0 ) } { ( 0 - 3 0 ) ( 0 - 6 0 ) ( 0 - 9 0 ) } = - 0 . 0 4 5 5 , $$
$$ \large L _ 2 ( 5 1 ) = \frac { ( 5 1 - 0 ) ( 5 1 - 6 0 ) ( 5 1 - 9 0 ) } { ( 3 0 - 0 ) ( 3 0 - 6 0 ) ( 3 0 - 9 0 ) } = + 0 . 3 3 1 5 , $$
$$ \large L _ 3 ( 5 1 ) = \frac { ( 5 1 - 0 ) ( 5 1 - 3 0 ) ( 5 1 - 9 0 ) } { ( 6 0 - 0 ) ( 6 0 - 3 0 ) ( 6 0 - 9 0 ) } = + 0 . 7 7 3 5 , $$
$$ \large L _ 4 ( 5 1 ) = \frac { ( 5 1 - 0 ) ( 5 1 - 3 0 ) ( 5 1 - 6 0 ) } { ( 9 0 - 0 ) (9 0 - 3 0 ) ( 9 0 -6 0 ) } = - 0 . 05 9 5 . $$
در نهایت، با توجه به معادله $$ y = \sum_{i=1}^n y_i L_i (x) $$، داریم:
$$ \large \begin {align*} \sin 5 1 ^ \circ & = 0 \times ( - 0 . 0 4 5 5 ) + 0 . 5 \times 0 . 3 3 1 5 \\ & \;\;\;\;\;+ 0 . 8 6 6 0 3 \times 0 . 7 7 3 5 + 1 \times ( - 0 . 0 5 9 5 ) \\ & = 0 .776 \end {align*} $$
مقدار دقیق $$ \sin 51^\circ $$ برابر با $$ 0.777 $$ است و میبینیم که دقت درونیابی مناسب است.
مثال ۳
میخواهیم تابع $$ f ( x ) = x ^ 2 $$ را در بازه $$ 1 \le x \le 3 $$ برای سه نقطه زیر درونیابی کنیم:
$$ \large \begin {align}
x _ 0 & = 1 & & & f ( x _ 0 ) & = 1 \\
x _ 1 & = 2 & & & f ( x _ 1 ) & = 4 \\
x _ 2 & = 3 & & & f ( x _ 2 ) & = 9 .
\end {align} $$
حل: چندجملهای درونیاب به صورت زیر به دست میآید:
$$ \large \begin {align}
P ( x ) & = { 1 } \cdot { x - 2 \over 1 - 2 }\cdot { x - 3 \over 1 - 3 } + { 4 } \cdot { x - 1 \over 2 - 1 } \cdot { x - 3 \over 2 - 3 } + { 9 } \cdot { x - 1 \over 3 - 1 } \cdot { x - 2 \over 3 - 2 } \\[10pt] & = x ^ 2 .
\end {align} $$
مثال ۴
میخواهیم $$ f ( x ) = x ^ 3 $$ را روی بازه $$ 1 \le x \le 4 $$ برای چهار نقطه زیر درونیابی کنیم:
$$ \large \begin {align*}
x _ 0 = 1 & & & f ( x _ 0 ) = 1 \\
x _ 1 = 2 & & & f ( x _ 1 ) = 8 \\
x _ 2 = 3 & & & f ( x _ 2 ) = 2 7 \\
x _ 3 = 4 & & & f ( x _ 3 ) = 6 4
\end {align*} $$
چندجملهای درونیاب به صورت زیر به دست میآید:
$$ \large \begin {align} P ( x ) & = { 1 } \cdot { x - 2 \over 1 - 2 } \cdot { x - 3 \over 1 - 3 } \cdot { x - 4 \over 1 - 4 } +{ 8 } \cdot { x - 1 \over 2 - 1 } \cdot { x - 3 \over 2 - 3 } \cdot { x - 4 \over 2 - 4 } \\ & \;\;\;\; + { 2 7 } \cdot { x - 1 \over 3 - 1 } \cdot { x - 2 \over 3 - 2 } \cdot { x - 4 \over 3 - 4 } + { 6 4 } \cdot { x - 1 \over 4 - 1 } \cdot { x - 2 \over 4 - 2 } \cdot { x - 3 \over 4 - 3 } \\[8pt] & = x ^ 3 \end {align} $$
مثال ۵
تابع $$ y = f ( x ) = x \sin ( 2 x + \pi / 4 ) + 1 $$ را با یک چندجملهای درجه سه تقریب بزنید. برای این کار، از نقاط داده شده زیر استفاده کنید:
| $$ 4 $$ | $$ 3 $$ | $$ 2$$ | $$ 1 $$ | $$ i $$ |
| $$ 2$$ | $$ 1$$ | $$ 0 $$ | $$ - 1 $$ | $$ x _ i $$ |
| $$-0.995$$ | $$1.349$$ | $$1.000$$ | $$ 1.937$$ | $$ y _ i = f ( x _ i ) $$ |
حل: بر اساس این نقاط، چندجملهایهای لاگرانژ را به عنوان توابع پایه چندجملهای تشکیل میدهیم:
$$ \large \begin {aligned}
L _ { 1 } ( x ) & = \frac { ( x - 0 ) ( x - 1 ) ( x - 2 ) } { - 6 } = \frac{ x ^ { 3 } - 3 x ^ { 2 } + 2 x } { - 6 } \\
L _ { 2 } ( x ) & = \frac { ( x + 1 ) ( x - 1 ) ( x - 2 ) } { 2 } = \frac { x ^ { 3 } - 2 x ^ { 2 } - x + 2 } { 2 } \\
L _ { 3 } ( x ) & = \frac { ( x + 1 ) ( x - 0 ) ( x - 2 ) }{ - 2 } = \frac { x ^ { 3 } - x ^ { 2 } - 2 x } { - 2 } \\
L _ { 4 } ( ( x ) & = \frac { ( x + 1 ) ( x - 0 ) ( x - 1 ) } { 6 } = \frac { x ^ { 3 } - x } { 6 } \end {aligned} $$
توجه کنید که در واقع، رابطه $$ L _ 1 ( x ) + L _ 2 ( x ) + L _ 3 ( x ) + L _ 4 ( x ) = 1 $$ برقرار است. چندجملهای درونیاب را میتوان با جمع وزندار توابع پایه به صورت زیر محاسبه کرد:
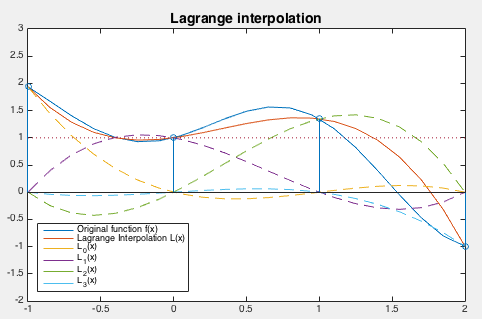
$$ \large \begin {align*} y & = 1 . 9 3 7 L _ { 1 } ( x ) + 1 . 0 L _ { 2 } ( x ) + 1 . 3 4 9 L _ { 3 } ( x ) - 0 . 9 9 5 L _ { 4 } ( x ) \\ & = 1 . 0 + 0 . 3 6 9 x + 0 . 6 4 3 x ^ { 2 } - 0 . 6 6 3 x ^ { 3 } \end {align*} $$
شکل زیر، نتیجه درونیابی لاگرانژ را نشان میدهد.
پیادهسازی تقریب با چند جمله ای لاگرانژ در متلب
کد متلب زیر تابع تقریب با چند جمله ای لاگرانژ در متلب را نشان میدهد.
1function y=lagrange(x,pointx,pointy)
2%
3%LAGRANGE approx a point-defined function using the Lagrange polynomial interpolation
4%
5% LAGRANGE(X,POINTX,POINTY) approx the function definited by the points:
6% P1=(POINTX(1),POINTY(1)), P2=(POINTX(2),POINTY(2)), ..., PN(POINTX(N),POINTY(N))
7% and calculate it in each elements of X
8%
9% If POINTX and POINTY have different number of elements the function will return the NaN value
10%
11% function wrote by: Calzino
12% 7-oct-2001
13%
14n=size(pointx,2);
15L=ones(n,size(x,2));
16if (size(pointx,2)~=size(pointy,2))
17 fprintf(1,'\nERROR!\nPOINTX and POINTY must have the same number of elements\n');
18 y=NaN;
19else
20 for i=1:n
21 for j=1:n
22 if (i~=j)
23 L(i,:)=L(i,:).*(x-pointx(j))/(pointx(i)-pointx(j));
24 end
25 end
26 end
27 y=0;
28 for i=1:n
29 y=y+pointy(i)*L(i,:);
30 end
31endبرای مثال، فرض کنید تعداد ۱۱ نقطه (۰ و ۱ و ۲ و ... و ۱۰) داریم و مقادیر متناظر آنها $$ y = x ^ 2 $$ هستند. میخواهیم، مقدار $$ y $$ را در $$ x = 2.5$$ به دست آوریم. بدین منظور، به صورت زیر از تابع متلب بالا استفاده میکنیم:
1n = 0:10;
2m = n.^2;
3y = lagrange(2.5,n,m);اگر برنامه اخیر را اجرا کنیم، نتیجه آن به صورت زیر خواهد بود:
6.2500
همانطور که میبینیم، این جواب در $$ y = x ^ 2 $$ صدق میکند.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای محاسبات عددی
- آموزش محاسبات عددی با MATLAB
- مجموعه آموزشهای دروس ریاضیات
- آموزش محاسبات عددی (مرور و حل مساله)
- روش ژاکوبی — به زبان ساده
- برازش منحنی (Curve Fitting) — به زبان ساده
- تقریب خطی — به زبان ساده
^^











خیلی عالی بود .
سلام
خیلی ممنون بابت انتشار این مطالب مفید و کمک کننده
خدا خبرتون بده
واقعا مگه خفن تر از این هم داریم هم متن آموزش هم فیلم آموزش هم فیلم حل مثال هم پروژه متلب هم فیلم پروژه متلب واقعا با اختلاف بهترین سایت آموزش عای ایرن هستید خیلی ممنون از فرادرس و استاد سراج حمیدی وامید زندی عزیز?????
سلام اسحاق عزیز.
از اینکه آموزشهای مجله فرادرس برایتان مفید بوده، بسیار خوشحالیم.
شاد و پیروز باشید.
سلام خسته نباشید
امکانش هست جواب این سوال رو کمک کنید .
چند جمله ای های الگرانژ را برای تابع جدولی زیر به دست آورید.
Xi=0,1,2,4
Fi=3,2,7,59
ممنون .
با سلام
آیا روشی وجود داره که بشه باهاش هر نعداد نقطه که داشته باشیم رو بهش بدیم و اون روش یا الگوریتم بهمون یک فرمول مشخص بده که دقیقاً از اون نقاط بگذره نه اینکه تقریب بزنه؟
سلام
اگر بخواهیم برای مثال 1 ویدئو پیاده سازی در متلب نمودار رسم کنیم چه دستوری رو باید وارد کنیم؟
چرا مجموع L ها در لاگرانژ برابر یک میشه؟؟؟
سلام.
وقتی تابع $$ f ( x ) = 1 $$ را درونیابی میکنیم، چندجملهای درونیاب (لاگرانژ) به صورت $$ P(x) =\sum _{k=1}^n f(x_k)L_k (x)=\sum _{k=1}^n L_k (x)$$ است. برای هر $$ x_1$$، … و $$x_n$$، چندجملهای مرتبه صفر $$P(x)=f(x)=1$$ دادهها را درونیابی میکند. از آنجا که چندجملهای درونیاب یکتاست، برای هر $$x$$، میتوان این رابطه را نوشت: $$ 1= P(x) =\sum _{k=1}^n L_k (x)$$.
از همراهی شما با مجله فرادرس سپاسگزاریم.