درون یابی اسپلاین — از صفر تا صد

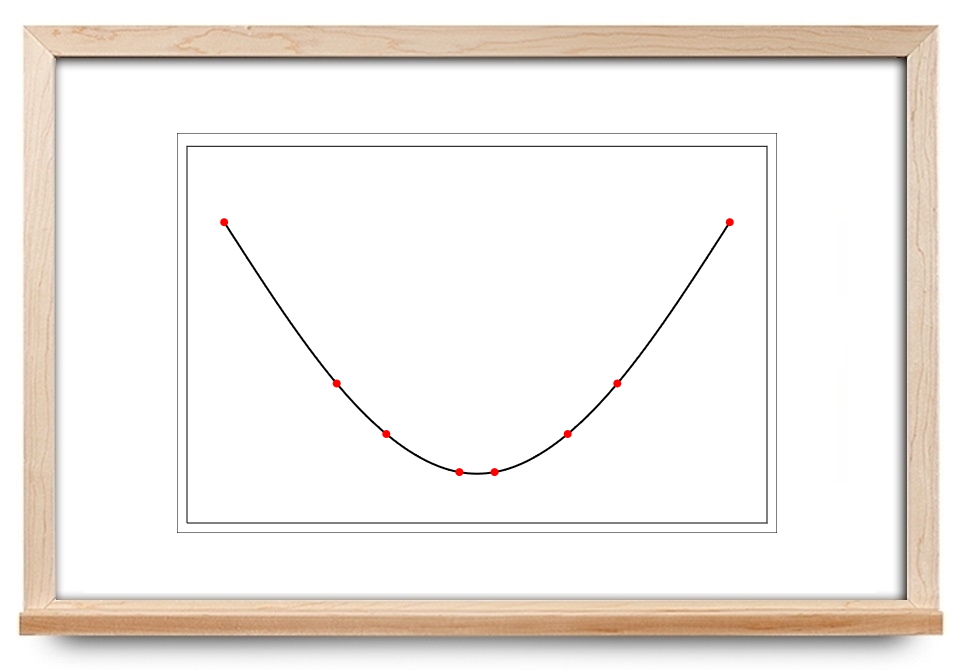
در آموزش‌های قبلی مجله فرادرس، با درون‌یابی با استفاده از چندجمله‌ای لاگرانژ آشنا شدیم. در این آموزش، درون‌یابی اسپلاین را معرفی می‌کنیم. در محاسبات عددی، «درون یابی اسپلاین» (Spline Interpolation) یک روش درون‌یابی است که در آن، درون‌یاب، نوع خاصی از یک چندجمله‌ای تکه‌ای است که یک «اسپلاین» (Spline) نامیده می‌شود. درون یابی اسپلاین اغلب نسبت به درون یابی چندجمله‌ای ترجیح داده می‌شود، زیرا حتی وقتی از چندجمله‌ای‌هایی با درجه پایین برای اسپلاین استفاده می‌شود، می‌توان به خطای درون‌یابی کمی دست یافت. درون یابی اسپلاین از مسئله «پدیده رونگه» (Runge's Phenomenon) جلوگیری می‌کند. در پدیده رونگه، هنگام استفاده از چندجمله‌ای‌های مرتبه بالا در درون‌یابی، ممکن است بین نقاط نوسان رخ دهد.

درون یابی اسپلاین

اسپلاین در ابتدا اصطلاحی بود که برای خط‌کش‌های کشسان به کار می‌رفت. این خط‌کش‌ها قابلیت خم شدن برای عبور از تعدادی از نقاط از پیش تعریف شده (گره) داشتند.

فیلم آموزش محاسبات عددی – مرور و حل مساله در فرادرس

کلیک کنید

از این اسپلاین‌ها برای تهیه نقشه‌های فنی در ساخت کشتی استفاده می‌شد.

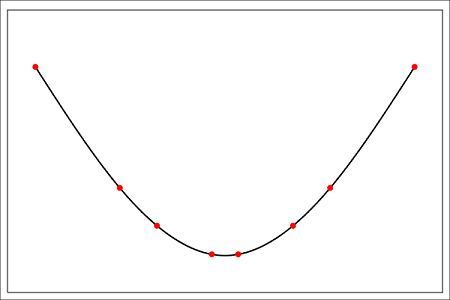
روش مدل‌سازی ریاضی شکل این خط‌کش‌های کشسانِ ثابت با $$ n + 1 $$ نقطه $$ \left \{ ( x _ i , y _ i ) : i = 0 , 1 , \cdots , n \right \} $$، در حقیقت، درون‌یابی بین همه زوج نقطه‌های $$ ( x _{i-1} , y _ {i - 1} ) $$ و $$ ( x _ i , y _ i ) $$ با استفاده از چندجمله‌ای $$ y = q _ i ( x ) $$ است که در آن، $$ i = 1,2, \cdots , n $$.

انحنای منحنی $$ y = f ( x) $$ به صورت زیر بیان می‌شود:

$$ \large \kappa = \frac { y^{\prime \prime} } { ( 1 + y' ^ 2 ) ^ { 3 / 2 } } $$

از آنجایی که شکل اسپلاین به گونه‌ای است که خمش را (تحت قید عبور از همه نقاط) کمینه کند، $$ y'$$ و $$ y ^{\prime \prime}$$ در همه جا و همه نقاط پیوسته خواهند بود. به عبارت دیگر، خواهیم داشت:

$$ \large \begin {cases} q' _ i ( x _ i ) = q' _ { i + 1 } ( x _ i ) \\ q^{\prime \prime} _ i ( x _ i ) = q^{\prime \prime} _ {i + 1 } ( x _ i ) \end {cases} \qquad 1 \le i \le n - 1 $$

این امر زمانی امکان‌پذیر است که چندجمله‌ای‌ها از درجه ۵ یا بالاتر باشند. روش کلاسیک برای استفاده از چندجمله‌ای درجه ۳، اسپلاین‌ مکعبی (Cubic Spline) نامیده می‌شود که در آن، مشتق اول پیوسته است، اما مشتق دوم خیر.

الگوریتم یافتن اسپلاین مکعبی درون‌یاب

در این بخش، ابتدا اسپلاین مکعبی را برای درون‌یابی دو نقطه بیان کرده و در ادامه، فرمول کلی آن را ارائه خواهیم کرد.

فیلم آموزش آنالیز عددی پیشرفته در فرادرس

کلیک کنید

درون یابی اسپلاین مکعبی بین دو نقطه

چندجمله‌ای مرتبه سوم $$ q ( x) $$ را در نظر بگیرید که زوج نقطه $$(x_1,y _ 1 ) $$ و $$ ( x _ 2 , y _2 )$$ را درون‌یابی می‌کند:

$$ \large \begin {align*} q ( x _ 1 ) & = y _ 1 \\
q ( x _ 2 ) & = y _ 2 \\
q' ( x _ 1 ) & = k _ 1 \\
q' ( x _ 2 ) & = k _ 2
\end {align*} $$

می‌توانیم فرم متقارن زیر را بنویسیم که تساوی‌های بالا در آن صدق می‌کنند:

$$ \large q ( x ) = \big ( 1 - t ( x ) \big) \, y _ 1 + t ( x ) \, y _ 2 + t ( x ) \big ( 1 - t ( x ) \big ) \Big( \big( 1 - t ( x ) \big)\, a + t ( x ) \, b \Big ) \;\;\;\; (1)$$

که در آن:

$$ \large \begin {align*} t ( x ) & = \frac { x - x _ 1 } { x _ 2 -x _ 1 } ,\;\;\;\; (2) \\ a & = k _ 1 ( x _ 2 - x _ 1 ) - ( y _ 2 - y _ 1 ) , \;\;\;\; (3)
\\ b & = - k _ 2 ( x _ 2 - x _ 1 ) + ( y _ 2 - y _ 1 ) . \;\; \; \; (4) \end {align*} $$

با توجه به تساوی زیر:

$$ \large q' = \frac { d q } { d x } = \frac { d q } { d t } \frac { d t } { d x } = \frac { d q } { d t } \frac { 1 } { x _ 2 - x _ 1 } $$

این روابط را خواهیم داشت:

$$ \large \begin {align*} q' & = \frac { y _ 2 - y _ 1 } { x _ 2 -x _ 1 } + ( 1 - 2 t ) \frac { a ( 1 - t ) + b t } { x _ 2 - x _ 1 } + t ( 1 - t ) \frac { b - a } { x _ 2 - x _ 1 } , \;\;\;\;(5) \\
\large q^{\prime \prime} & = 2 \frac { b - 2 a + ( a - b ) 3 t } { { ( x _ 2 -x _ 1 ) } ^ 2 } . \;\;\;\; (6) \end {align*} $$

با قرار دادن $$ x = x _ 1 $$ و $$ x = x _ 2 $$، به ترتیب در معادلات (۵) و (۶) با استفاده از (۲)، مشتق‌های اول $$ q' ( x _ 1 ) = k _ 1$$ و $$ q' (x_ 2 ) = k _ 2 $$ و مشتق‌های دوم زیر را به دست خواهیم آورد:

$$ \large \begin {align*} q^{\prime \prime} ( x _ 1 ) = 2 \frac { b - 2 a } { { ( x _ 2 - x _ 1 ) } ^ 2 } \;\;\;\; (7)
\\ q^{\prime\prime} ( x _ 2 ) = 2 \frac { a - 2 b } { { ( x _ 2 - x _ 1 ) } ^ 2 } \;\;\;\; (8) \end {align*} $$

فرمول عمومی درون یابی اسپلاین مکعبی

اکنون اگر $$ (x_i,y_i)  $$ را برای $$ i = 0, 1 , ... , n $$ و به عنوان $$ n + 1 $$ نقطه در نظر بگیریم، تعداد $$n$$ چندجمله‌ای مرتبه سوم درون‌یاب $$ y $$ در بازه $$ x _{i-1} \le x \le x _i$$ برای $$ i= 1 , ... , n$$ خواهیم داشت، به گونه‌ای که $$ q' _ i ( x _ i ) = q' _ {i+1} (x_i) $$ برای $$ i = 1 , ... , n - 1 $$ برقرار است:

$$ \large q _ i = ( 1 - t ) \, y _ { i - 1 } + t \, y _ i + t ( 1 -t ) \big ( ( 1 - t ) \, a _ i + t \, b _ i \big ) \;\;\;\; (9)$$

که در آن، $$ i = 1 , 2 , ... , n $$ و $$ t = \frac {x - x _{i-1} } {x _ i - x _ {i-1}} $$ است و در نتیجه، $$n$$ چندجمله‌ای خواهیم داشت که با یکدیگر تابعی مشتق‌پذیر در بازه $$ x _ 0 \le x \le x _ n $$ تعریف می‌کنند و برای $$ i = 1 , ... , n $$ داریم:

$$ \large a _ i = k _ { i - 1 } ( x _ i - x _ { i - 1 } ) - ( y _ i - y _ { i - 1 } ) \;\;\;\; (10) $$

$$ \large b _ i = - k _ i ( x _ i - x _ { i - 1 } ) + (y _ i - y _ { i - 1 } ) \;\;\;\; (11) $$

که در آن:

$$ \large \begin {align*} k _ 0 & = q' _ 1 ( x _ 0 ) \;\;\;\;\; (12)\\
k _ i & = q _ i' ( x _ i ) = q _ { i + 1 }' ( x _ i ) \qquad i = 1 , \dotsc , n - 1 \;\;\;\; (13)\\
k _ n & = q _ n' ( x _ n ) \;\;\;\;\; (14)\end {align*} $$

اگر دنباله $$ k _ 0$$، $$ k _ 1$$، ... و $$ k _ n$$ به گونه‌ای باشد که برای $$ i = 1 , ... , n - 1 $$ تساوی $$ q ^{\prime \prime } _ i ( x _ i ) = q^{\prime \prime }_{i+1} ( x _ i ) $$ برقرار باشد، آنگاه تابع حاصل یک مشتق دوم پیوسته نیز خواهد داشت.

پس می‌توان به طور خلاصه گفت که الگوریتم روش درون یابی اسپلاین به صورت زیر است:

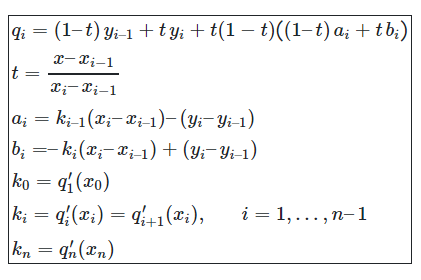
از معادلات (۷)، (۸)، (۱۰) و (۱۱) رابطه زیر را برای $$ i = 1 , ... , n - 1 $$ نتیجه می‌گیریم:

$$ \large \frac { k _ { i - 1 } } { x _ i - x _ { i - 1 } } + \left ( \frac { 1 } { x _ i - x _ { i - 1 } } + \frac { 1 }{ { x _ { i + 1 } - x _ i } } \right ) 2 k _ i + \frac { k _ { i + 1 } } { { x _ { i + 1 } - x _ i } } \\ \large =
3 \left ( \frac { y _ i - y _ { i - 1 } } { { ( x _ i - x _ { i - 1 } ) } ^ 2 } + \frac { y _ { i + 1 } - y _ i } { { ( x _ { i + 1 } - x _ i ) } ^ 2 } \right ) \;\;\;\;\; (15)$$

روابط (۱۵) در حقیقت $$ n - 1 $$ معادله خطی برای $$ n + 1 $$ مقدار $$ k _ 0 $$، $$ k _ 1 $$، ... و $$ k _ n $$ هستند.

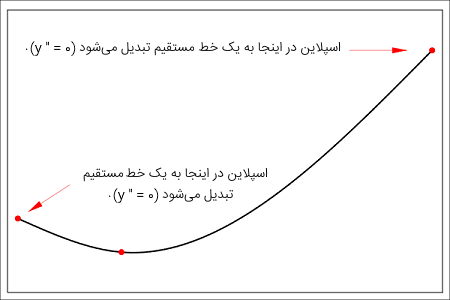
در خط‌کش‌های کشسان که مدل درون یابی اسپلاین هستند، سمت چپ یا چپ‌‌ترین گره یا همان نقطه و سمت راست یا راست‌ترین گره خط‌کش می‌تواند آزادانه حرکت کند و به همین دلیل، با $$ q^{\prime\prime} = 0$$ فرم یک خط مستقیم را به خود می‌گیرد. از آنجایی که $$q^{\prime \prime}$$ باید یک تابع پیوسته از $$ x $$ باشد، برای اسپلاین‌های طبیعی (Natural Splines) علاوه بر $$ n - 1 $$ معادله خطی (۱۵)، باید داشته باشیم:

$$ \large \begin {align*} q^ {\prime \prime} _ 1 ( x _ 0 ) & = 2 \frac { 3 ( y _ 1 - y _ 0 ) -( k _ 1 + 2 k _ 0 ) ( x _ 1 - x _ 0 ) } { { ( x _ 1 - x _ 0 ) } ^ 2 } = 0 , \\ q^ {\prime \prime} _ n ( x _ n ) & = - 2 \frac { 3 ( y _ n - y _ { n - 1 } ) - ( 2 k _ n + k _ { n - 1 } ) ( x _ n - x _ { n - 1 } ) } { { ( x _ n - x _ { n - 1 } ) } ^ 2 } = 0 \end {align*} $$

این یعنی:

$$ \large \begin{align*} \frac { 2 } { x _ 1 - x _ 0 } k _ 0 +\frac { 1 } { x _ 1 - x _ 0 } k _ 1 & = 3 \frac { y _ 1 - y _ 0 } { ( x _ 1 - x _ 0 ) ^ 2 } , \;\; \;\;\; (16) \\ \frac { 1 } { x _ n - x _ { n - 1 } } k _ { n - 1 } + \frac { 2 } { x _ n - x _ { n - 1 } } k _ n & = 3 \frac { y _ n - y _ { n - 1 } } { ( x _ n - x _ { n - 1 } ) ^ 2 } . \;\;\;\; (17) \end {align*} $$

در نهایت، (۱۵) همراه با (۱۶) و (۱۷)، تعداد $$ n + 1 $$ معادله خطی را تشکیل می‌دهند که به صورت یکتا $$ n + 1 $$ پارامتر $$ k_0$$، $$ k _ 1$$، ... و $$ k _ n $$ را تعریف می‌کنند.

موارد دیگری نیز وجود دارند که می‌توان آن‌ها را نیز در نظر گرفت: «اسپلاین مقید» (Clamped Spline) که شیب را در انتهای اسپلاین مشخص می‌کند، و «اسپلاین غیرگره‌ای» (Not-a-knot Spline)، که در آن، مشتق سوم نیز در نقاط $$ x _ 1 $$ و $$ x _ { N - 1 } $$ باید پیوسته باشد. برای اسپلاین غیرگره‌ای، معادلات زیر را نیز داریم:

$$ \large q^{\prime \prime \prime} _ 1 ( x _ 1 ) = q^{\prime \prime \prime} _ 2 ( x _ 1 ) \\ \large \Rightarrow \frac { 1 } { \Delta x _ 1 ^ 2 } k _ 0 + \left ( \frac { 1 } { \Delta x _ 1 ^ 2 } - \frac { 1 } { \Delta x _ 2 ^ 2 } \right ) k _ 1 - \frac { 1 } { \Delta x _ 2 ^ 2 } k _ 2 \\ \large = 2 \left ( \frac { \Delta y _ 1 } { \Delta x _ 1 ^ 3 } - \frac { \Delta y _ 2 } { \Delta x _ 2 ^ 3 } \right ) $$

$$ \large q^{\prime \prime \prime} _ { n - 1 } ( x _ { n - 1 }) = q^{\prime \prime \prime} _ n ( x _ { n - 1 } ) \\ \large \Rightarrow \frac { 1 } { \Delta x _ { n - 1 } ^ 2 } k _ { n - 2 } + \left ( \frac { 1 } { \Delta x _ { n - 1 } ^ 2 } - \frac { 1 }{ \Delta x _ n ^ 2 } \right ) k _ { n - 1 } - \frac { 1 } { \Delta x _ n ^ 2 } k _ n \\ \large = 2 \left ( \frac { \Delta y _ { n - 1 } }{ \Delta x _ { n - 1 } ^ 3 } - \frac { \Delta y _ n } { \Delta x _ n ^ 3 } \right ) $$

که در آن، $$ \Delta x _ i = x _ i - x _ { i - 1 } $$ و $$ \Delta y _ i = y _ i - y _ { i - 1 } $$.

مثال درون یابی اسپلاین

می‌خواهیم دو چندجمله‌ای برای درون‌یابی سه نقطه $$ ( -1, 0.5)$$، $$ (0, 0 ) $$ و $$ ( 3 , 3 )$$ با استفاده از روش درون یابی اسپلاین به دست آوریم. با نوشتن معادلات لازم، به دستگاه معادلات سه‌قطری زیر برای مقادیر $$ k _ 0 $$، $$ k _ 1 $$ و $$ k _ 2 $$ می‌رسیم:

$$ \large \begin {bmatrix} a _ { 1 1 } & a _ { 1 2 } & 0 \\
a _ { 2 1 } & a _ { 2 2 } & a _ { 2 3 } \\
0 & a _ { 3 2 } & a _ { 3 3 } \\
\end {bmatrix} \begin {bmatrix}
k _ 0 \\ k _ 1 \\ k _ 2 \\ \end {bmatrix} =
\begin {bmatrix} b _ 1 \\ b _ 2 \\ b _ 3 \\
\end {bmatrix} $$

که در آن:

$$ \large \begin {align*} a _ { 1 1 } & = \frac { 2 } { x _ 1 - x _ 0 } \\
a _ { 1 2 } & = \frac { 1 } { x _ 1 - x _ 0 } \\
a _ { 2 1 } & = \frac { 1 } { x _ 1 - x _ 0 } \\
a _ { 2 2 } & = 2 \ \left ( \frac { 1 } { x _ 1 - x _ 0 } + \frac { 1 } { { x _ 2 - x _ 1 } } \right ) \\
a _ {2 3 } & = \frac { 1 } { { x _ 2 - x _ 1 } } \\
a _ { 3 2 } & = \frac { 1 } { x _ 2 - x _ 1 } \\
a _ { 3 3 } & = \frac { 2 } { x _ 2 - x _ 1 } \\
b _ 1 & = 3\ \frac { y _ 1 - y _ 0 } { ( x _ 1 - x _ 0 ) ^ 2 } \\ b _ 2 & = 3 \ \left ( \frac { y _ 1 - y _ 0 } { { ( x _ 1 -x _ 0 ) } ^ 2 } + \frac { y _ 2 - y _ 1 } { { ( x _ 2 -x _ 1 ) } ^ 2 } \right ) \\ b _ 3 & = 3 \ \frac { y _ 2 - y _ 1 } { ( x _ 2 -x _ 1 ) ^ 2 } \end {align*} $$

بنابراین، برای سه نقطه $$ ( -1, 0.5)$$، $$ (0, 0 ) $$ و $$ ( 3 , 3 )$$ داریم:

$$ \large k _ 0 = - 0 . 6 8 7 5 \ ,\ k _ 1 = - 0 . 1 2 5 0 \ ,\ k _ 2 = 1 . 5 6 2 5 $$

و از معادلات (۱۰) و (۱۱)، خواهیم داشت:

$$ \large \begin {align*} a _ 1 & = k _ 0 ( x _ 1 - x _ 0 ) - ( y _ 1 - y _ 0 ) = - 0 . 1 8 7 5 \\ \large b _ 1 & = - k _ 1 ( x _ 1 - x _ 0 ) + ( y _ 1 - y _ 0 ) = - 0 . 3 7 5 0 \\ \large a _ 2 & = k _ 1 ( x _ 2 - x _ 1 ) - ( y _ 2 - y _ 1 ) = - 3 . 3 7 5 0 \\ b _ 2 & = -k _ 2 ( x _ 2 - x _ 1 ) + ( y _ 2 - y _ 1 ) = - 1 . 6 8 7 5 \end {align*} $$

در شکل ۲، تابع اسپلاین از دو چندجمله‌ای مکعبی $$ q _ 1 ( x ) $$ و $$ q _ 2 ( x ) $$ تشکیل شده که در رابطه (۹)‌ بیان شد.

پیاده‌سازی درون یابی اسپلاین در متلب

درون یابی اسپلاین در متلب در قالب تابع cubic_spline به صورت زیر است:

فیلم آموزش محاسبات عددی با متلب MATLAB در فرادرس

کلیک کنید

1function [ XX,YY ] = cubic_spline( X,Y,C0,CN,hh )
2% CUBIC_SPLINE: Cubic spline interpolation for given data X and Y.
3%   
4%   INPUT:
5%   X: Given X data
6%   Y: Given Y data
7%   C0: boundary condition (C0 = 0: natural spline)
8%   CN: boundary condition (CN = 0: natural spline)
9%   hh: Increment for new x and y data
10%
11%   OUTPUT:
12%   XX: New x data
13%   YY: New y data
14%
15% -----------------------------------------------------------------------
16%   Created by Joshua Simon. 
17%   Date: 02.06.2018
18% -----------------------------------------------------------------------
19counter = 0;
20index = 1;
21
22% Get dimensions
23n = max(size(X))-1;
24
25% Calculate distance h
26h = zeros(n,1);
27
28for k = 1:n
29    h(k) = X(k+1) - X(k);
30    % Counting new x values 
31    for j = X(k):hh:X(k+1)-hh       
32        counter = counter +1;
33    end
34end
35
36% Calculate my, lambda, delta
37my = zeros(n-1,1);
38lambda = zeros(n-1,1);
39delta_vor = zeros(n,1);
40
41for k = 1:n-1
42    my(k) = h(k) / (h(k+1)+h(k));
43    lambda(k) = h(k+1) / ( h(k+1)+h(k));
44    delta_vor(k) = 6/(h(k+1)+h(k)) * ((Y(k+2)-Y(k+1))/h(k+1) - (((Y(k+1)-Y(k))/h(k))));
45end
46
47delta = [0;delta_vor];
48my_mat = [my;0];
49lambda_mat = [0;lambda];
50
51% Assemble coefficients matrix S
52S = 2*eye(n+1) + diag(my_mat,-1) + diag(lambda_mat,1);
53
54% Solve system of linear equations
55M = S\delta;
56M(1) = C0;                                      %boundary condition
57M(end) = CN;                                    %boundary condition
58
59% Calculating coefficients of cubic spline
60a = zeros(n,1);
61b = zeros(n,1);
62c = zeros(n,1);
63d = zeros(n,1);
64
65for k = 1:n
66    a(k) = Y(k);
67    b(k) = (Y(k+1)-Y(k))/h(k) - (h(k)/6) * (2*M(k)+M(k+1));
68    c(k) = M(k)/2;
69    d(k) = (M(k+1)-M(k))/(6*h(k));
70end
71
72% Cubic spline function
73c_Spline = @(x,i) a(i) + b(i).*(x-X(i)) + c(i).*(x-X(i)).^2 + d(i).*(x-X(i)).^3;
74
75XX = zeros(1,counter);
76YY = zeros(1,counter);
77
78% Assmeble new x and y data
79for k = 1:n
80    for j = X(k):hh:X(k+1)-hh
81         XX(index) = j;
82         YY(index) = c_Spline(j,k);
83         index = index + 1;
84    end
85end
86
87% Set last element of new data
88XX = [XX,X(end)];
89YY = [YY,c_Spline(X(end),n)];
90
91end

برای آزمایش تابع بالا، کد زیر را می‌نویسیم:

1% cubic_spline_example
2% -----------------------------------------------------------------------
3% Interpolate given data with a natural cubic spline.
4%
5% Created by Joshua Simon.
6% Date: 02.06.2018
7% -----------------------------------------------------------------------
8
9% Data
10X = [-2, -1, 1, 3, 4, 5];
11Y = [2, 1, 3, 1, 0, 2];
12
13% Interpolation
14[XX,YY] = cubic_spline(X,Y,0,0,0.1);
15
16% Plot
17figure
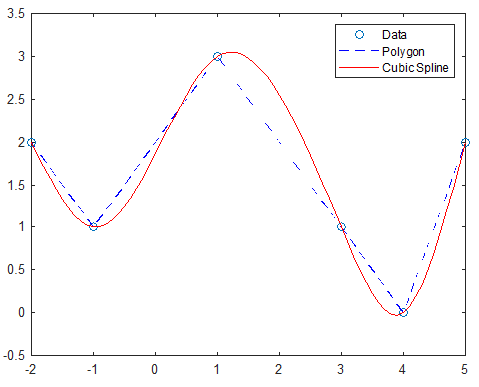
18plot(X,Y,'o',X,Y,'b--',XX,YY,'r')
19legend('Data','Polygon','Cubic Spline')

شکل حاصل از اجرای این برنامه به صورت زیر است:

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های محاسبات عددی
• آموزش محاسبات عددی با MATLAB
• مجموعه آموزش‌های دروس ریاضیات
• آموزش محاسبات عددی (مرور و حل مساله)
• روش ژاکوبی — به زبان ساده
• برازش منحنی (Curve Fitting) — به زبان ساده
• تقریب خطی — به زبان ساده

^^