فرادرسماتریس معین مثبت (Positive Definite Matrix) — به زبان ساده
بردارها و ماتریس‌ها ابزارهای «جبر خطی» (Linear Algebra) هستند. درست به مانند معادلات ریاضی که براساس اعداد حقیقی ساخته شده‌اند و بوسیله جبر و حسابان حل می‌شوند، ابزار حل معادلات ماتریسی و برداری نیز جبر خطی است. یکی از خصوصیاتی جالبی که در جبر خطی به آن پرداخته می‌شود «ماتریس معین مثبت» (Positive Definite) و ویژگی‌های آن است. در این نوشتار به بررسی خصوصیات ماتریس‌ها از دیدگاه «مُعیَن بودن» (Definiteness) می‌پردازیم. برای آشنایی بیشتر با مباحث جبر خطی و ماتریس‌ها بهتر است مطلب ماتریس‌ها — به زبان ساده و بردار ویژه و مقدار ویژه — از صفر تا صد را مطالعه کنید. همچنین خواندن نوشتارهای ترانهاده ماتریس — به زبان ساده و اثر ماتریس (Trace) در جبر خطی — به زبان ساده نیز خالی از لطف نیست.
ماتریس معین مثبت
برای درک مفهوم ماتریس معین مثبت ابتدا بعضی از خصوصیات ماتریس‌ها را مرور می‌کنیم. نخست و در همین راستا ماتریس مربعی و ماتریس متقارن را معرفی می‌کنیم.
در جبر خطی، ماتریس $$M$$ را مربعی گویند اگر تعداد سطرها و ستون‌های آن یکسان باشد. معمولا یک ماتریس مربعی را به صورت $$M_{n\times n}$$ نشان می‌دهند و به این ترتیب مشخص می‌شود که تعداد سطرها و ستون‌های آن برابر با $$n$$ است.
اگر عنصر یا درایه قرار گرفته در سطر $$i$$ و ستون $$j$$ام ماتریس $$M$$ را با $$m_{ij}$$ نشان دهیم، مشخص است که عناصر قطر اصلی این ماتریس به صورت $$m_{ii}$$ خواهند بود. از طرفی ماتریس مربعی $$M$$ را متقارن می‌گویند اگر عناصر بالا و پایین قطر اصلی آن متناظرا یکسان باشند. به بیان دیگر عناصر یا درایه‌های آن دارای خاصیت زیر باشند.
$$\large m_{ij} = m_{ji}, \;\; i,j = 1 , 2, \ldots , n$$
به این ترتیب مشخص است که اگر $$M$$ ماتریس متقارن باشد، حتما با «ترانهاده» (Transpose) خودش برابر است. یعنی رابطه زیر برای ماتریس متقارن $$M$$ برقرار است. توجه داشته باشید که منظور از $$M^T$$ ترانهاده ماتریس $$M$$ است.
$$\large M^T=M$$
برای مثال ماتریس $$A$$ که در ادامه معرفی شده است یک ماتریس متقارن است.
$$\large {\displaystyle A={\begin{bmatrix}1&7&3\\7&4&-5\\3&-5&6\end{bmatrix}}}$$
تعریف ماتریس معین مثبت
حال که با مفاهیم اولیه ماتریس‌ها آشنا شدیم، به معرفی ماتریس معین مثبت می‌پردازیم. ماتریس $$M$$ که متقارن و مربعی $$n \times n$$ است را معین مثبت می‌نامیم اگر برای هر بردار ستونی غیر صفر $$z$$ با $$n$$ سطر، حاصل $$z^TMz$$ یک مقدار عددی مثبت باشد. این موضوع را به بیان ریاضی به شکل زیر نشان می‌دهیم.
$$ \large {\displaystyle M{\text{ positive definite}}\quad \iff \quad z^{\textsf {T}}Mz>0{\text{ for all }}z\in \mathbb {R} ^{n}\setminus \mathbf {0} }$$
نکته: منظور از $$z\in \mathbb {R} ^{n}\setminus \mathbf {0} $$ بردارهای غیر صفر در فضای $$n$$ بُعدی است.
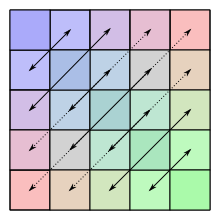
همانطور که در رابطه بالا مشاهده می‌کنید، در تعریف ماتریس معین مثبت، از یک بردار دلخواه $$z$$ استفاده شده است که همه عناصر آن صفر نیستند. در نتیجه این بردار دارای یک جهت است. وقتی که ماتریس $$M$$ را در بردار $$z$$ ضرب می‌کنیم، جهت بردار $$z$$ را تغییر داده‌ایم. واضح است که ماتریس $$M$$ روی بردار $$z$$ اثر کرده و با تبدیل صورت گرفته، بردار حاصل یا $$Mz$$ تغییر جهت داده است.
اگر ماتریس $$M$$ معین مثبت باشد، می‌توان نتیجه گرفت که با ضرب این ماتریس در بردار $$z$$ میزان تغییر جهت در بردار حاصل، کمتر از $$\frac{\pi}{2}$$ است. به تصویر زیر دقت کنید. به این ترتیب به نظر می‌رسد جهت بردار عکس نخواهد شد. یعنی زاویه بین بردار $$z$$ و تبدیل یافته آن که با $$Mz$$ نشان داده می‌شود، کمتر از $$\frac{\pi}{2}$$ است. در نتیجه $$cos \theta$$ منفی نخواهد شد. به این ترتیب رابطه $$z^TMz$$ همیشه مثبت است.
$$\large z^TMz=|z|.|Mz|.com \theta>0 $$
در اینجا منظور از $$|z|$$ و $$|Mz|$$ اندازه بردارهای حاصل است.
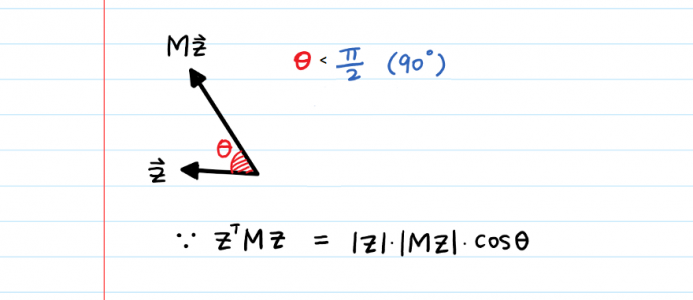
مثال ۱
«ماتریس همانی» (Identity Matrix) با بُعد n یک ماتریس معین مثبت است. در اینجا برای مثال از ماتریس همانی با بُعد $$n=2$$ استفاده می‌کنیم. فرض کنید ماتریس همانی با درجه ۲ را که به صورت $$ {\displaystyle I={\begin{bmatrix}1&0\\0&1\end{bmatrix}}}$$ نوشته می‌شود، در اختیار داریم. باید نشان دهیم این ماتریس معین مثبت است. فرض کنید بردار $$z^T$$ را به صورت $$[a b]$$ باشد. در این صورت محاسبات زیر را برای نشان دادن معین مثبت بودن ماتریس $$I$$ انجام می‌دهیم.
$$ \large {\displaystyle z^{\textsf {T}}Iz={\begin{bmatrix}a&b\end{bmatrix}}{\begin{bmatrix}1&0\\0&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}=a^{2}+b^{2}}$$
از آنجایی که طرف راست همیشه مثبت است (با فرض اینکه $$a$$ یا $$b$$ مثبت باشند) می‌توان ماتریس همانی را معین مثبت نامید.
مثال ۲
ماتریس مربعی و متقارن $$M$$ را به صورت زیر در نظر بگیرید. باید نشان دهیم که این ماتریس معین مثبت است.
$$ \large {\displaystyle M={\begin{bmatrix}2&-1&0\\-1&2&-1\\0&-1&2\end{bmatrix}}}$$
براساس تعریف ارائه شده، محاسبات زیر را برای بردار $$z$$ که حداقل یک درایه غیر صفر داشته و به صورت $$[a b c ]^T$$ نشان داده می‌شود، انجام می‌دهیم.
$$ \large {\displaystyle {\begin{aligned}z^{\textsf {T}}Mz=\left(z^{\textsf {T}}M\right)z&={\begin{bmatrix}(2a-b)&(-a+2b-c)&(-b+2c)\end{bmatrix}}{\begin{bmatrix}a\\b\\c\end{bmatrix}}\\&=(2a-b)a+(-a+2b-c)b+(-b+2c)c\\&=2a^{2}-ba-ab+2b^{2}-cb-bc+2c^{2}\\&=2a^{2}-2ab+2b^{2}-2bc+2c^{2}\\&=a^{2}+a^{2}-2ab+b^{2}+b^{2}-2bc+c^{2}+c^{2}\\&=a^{2}+(a-b)^{2}+(b-c)^{2}+c^{2}\end{aligned}}}$$
در سطر آخر این تساوی‌ها مشاهده می‌کنید که همه جملات مثبت هستند در نتیجه ماتریس $$M$$ معین مثبت است. اگر $$a=b=c=0$$ باشد، جمله آخر صفر خواهد شد ولی این رابطه بیان می‌کند که بردار $$z$$ یک بردار صفر است که در تعریف ماتریس معین مثبت این شرط برای بردار $$z$$ وجود ندارد.
مثال ۳
اگر $$A$$ یک ماتریس معکوس‌پذیر باشد، آنگاه $$A^TA$$ یک ماتریس معین مثبت است. یعنی داریم:
$$ \large {\displaystyle z^{\textsf {T}}A^{\textsf {T}}Az=(Az)^{\textsf {T}}(Az)=\|Az\|^{2}>0,}$$
طرف راست رابطه بنا به معکوس‌پذیری ماتریس $$A$$ صحیح است زیرا اگر $$A$$ معکوس‌پذیر باشد، برای هر بردار غیر صفر مثل $$z$$ رابطه زیر صادق می‌کند.
$$ ||z|| \neq 0 \rightarrow Iz=(A^{-1}A)z \rightarrow Az \neq 0$$
مثال ۴
مثبت یا منفی بودن درایه‌های ماتریس در معین مثبت بودن آن تاثیر گذار نیست. پس ممکن است ماتریس $$N$$ که همه درایه‌های آن مثبت است، ماتریس معین مثبت نباشد. برای نشان دادن این موضوع از ماتریس زیر که درایه‌های آن همگی مثبت هستند استفاده می‌کنیم.
$$ \large {\displaystyle N={\begin{bmatrix}1&2\\2&1\end{bmatrix}},}$$
این ماتریس معین مثبت نیست، زیرا برای بردار $$z=[-1 1]^T$$ رابطه زیر را خواهیم داشت.
$$ \large {\displaystyle {\begin{bmatrix}-1&1\end{bmatrix}}N{\begin{bmatrix}-1&1\end{bmatrix}}^{\textsf {T}}=-2<0.}$$
به این ترتیب با در نظر گرفتن یک مثال برای بردار $$z$$ و ماتریسی که همه درایه‌های آن مثبت بود نتوانستیم معین مثبت بودن ماتریس $$N$$ را نشان دهیم.
ماتریس نیمه معین مثبت
مطابق با آنچه در مورد ماتریس معین مثبت گفته شد، می‌توان «ماتریس نیمه معین مثبت» (Positive Semi-definite Matrix) را نیز تعریف کرد.
به بیان ریاضی ماتریس مربعی و متقارن $$M$$ را نیمه معین مثبت می‌گویند اگر رابطه زیر برای هر بردار غیر صفر $$z$$ برقرار باشد.
$$ \large {\displaystyle M{\text{ positive semi-definite}}\quad \iff \quad z^{\textsf {T}}Mz\geq 0{\text{ for all }}z\in \mathbb {R} ^{n}\setminus \mathbf {0} }$$
نکته: گاهی به ماتریس نیمه معین مثبت، ماتریس «معین نامنفی» (Non-negative Definite) نیز می‌گویند.
ماتریس معین منفی و نیمه معین منفی
برای ماتریس مربعی $$M$$ می‌توان خاصیت «معین منفی» (Negative Definite) و «نیمه معین منفی» (Negative Semi-definite) را نیز مشخص کرد.
ماتریس مربعی و متقارن $$M$$ را ماتریس معین منفی می‌نامیم اگر برای هر بردار غیر صفر $$z$$ رابطه زیر برقرار باشد.
$$ \large {\displaystyle M{\text{ negative definite}}\quad \iff \quad z^{\textsf {T}}Mz<0{\text{ for all }}z\in \mathbb {R} ^{n}\setminus \mathbf {0} }$$
و همچنین ماتریس $$M$$ را نیمه معین منفی می‌نامیم اگر خاصیت زیر برقرار باشد.
$$\large {\displaystyle M{\text{ negative semi-definite}}\quad \iff \quad z^{\textsf {T}}Mz\leq 0{\text{ for all }}z\in \mathbb {R} ^{n}\setminus \mathbf {0} }$$
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس ریاضیات
- آموزش ریاضیات عمومی 2
- آموزش جبر خطی
- مجموعه آموزش‌های آمار و احتمالات
- بردار ویژه و مقدار ویژه — از صفر تا صد
- معکوس ماتریس یا ماتریس وارون – به زبان ساده
^^
سلام خیلی خوب خدا خیرتون بده.
از همه بهتر اون قسمت بود که با میزان چرخش بردار ها توضیح دادین. با اون همه چی حل شد
سلام، خدا خیرتون بده ، خیلی خوب متوجه شدم
با سلام و احترام و تشکر بابت آموزش بسیار خوبتون
فقط بر اساس متونی که بنده مطالعه کردم، ماتریس های نیمه مثبت معین لزوماً متقارن نیستند. ولی از میان ماتریس های نیمه مثبت معین، ماتریس هایی که متقارن هستند دارای ویژگی های جالبی هستند که برای علوم داده دارای جذابیت است … به عنوان مثال، تمامی بردارهای ویژه آن دوبه دو متعامد هستند. از جمله این ماتریس ها، ماتریس کواریانس می باشد.
سلام
خیلی ممنون