تحلیل عاملی و پیاده‌ سازی آن در پایتون — به زبان ساده

یکی از روش‌های چند متغیره به منظور کاهش ابعاد یک مسئله با متغیرهای زیاد، استفاده از «تحلیل عاملی» (Factor Analysis) است. در این روش با استفاده از رابطه‌ای که بین متغیرهای قابل مشاهده وجود دارد، متغیرهای جدید ایجاد شده و مدل‌سازی و تحلیل‌ها، براساس آن‌ها صورت می‌گیرد. به چنین متغیرهایی «عامل» (Factor) گقته می‌شود. نوع انتخاب این متغیرها به شکلی است که بیشترین «تغییرات» (Variation) را توجیه کنند. در نتیجه با استفاده از تجزیه واریانس یا معیارهای پراکندگی، این عامل‌ها شناسایی شده و به کار گرفته می‌شوند. در این نوشتار به معرفی و آشنایی با تحلیل عاملی و نحوه پیاده‌سازی آن در پایتون می‌پردازیم و به کمک مثال‌های کاربردی، شیوه اجرای آن را فرا می‌گیریم.

برای آشنایی بیشتر با موضوع تحلیل عاملی بهتر است مطالب تحلیل مولفه اساسی (PCA)  و متغیر پنهان در مدل‌ ساختاری --- به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای هم خطی در مدل رگرسیونی — به زبان ساده و تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست.

آشنایی با تحلیل عاملی و پیاده‌ سازی آن در پایتون

تحلیل عاملی یا به اختصار FA یکی از روش‌های تحلیل اکتشافی (Exploratory) در آمار محسوب می‌شود. به کمک این تحلیل قادر هستیم متغیرهای پنهان (Latent Variables) را با استفاده از متغیرهای قابل مشاهده (Observable Variables) جستجو و محاسبه کنیم. به این ترتیب با استفاده از تکنیک FA می‌توانیم ابعاد یا متغیرهای مربوط به مدل‌سازی در یک مسئله پیچیده را کاهش دهیم. در نتیجه FA را یک روش برای کاهش بُعد (Dimension Reduction) یک مسئله پیچیده نیز می‌توان در نظر گرفت.

فیلم آموزش طراحی و تحلیل آزمایش ها با SPSS و مینی تب Minitab در فرادرس

کلیک کنید

از تحلیل عاملی در حوزه‌های مختلفی استفاده می‌شود. برای مثال در تحقیقات بازار، روان‌شناسی، علوم مالی و تحقیق در عملیات تحلیل عاملی به کار گرفته می‌شود. به عنوان نمونه در حوزه علوم مرتبط با تحقیقات بازار، تحلیل عاملی می‌تواند میزان حساسیت مشتریان نسبت به تغییرات قیمت را برآورد کند. همچنین از این تکنیک برای شناخت تمایل مشتری برای خرید از یک نام تجاری خاص می‌توان استفاده کرد.

در این نوشتار با عناوین زیر آشنا خواهیم شد:

• تحلیل عاملی (Factor Analysis)
• انواع روش‌های تحلیل عاملی
• محاسبات در تحلیل عاملی
• تعیین تعداد عامل‌ها
• تحلیل عاملی و تحلیل مولفه‌های اصلی
• آزمون کفایت
• تفسیر نتایج حاصل از تحلیل عاملی

به این ترتیب در بخش اول، تعریف اولیه‌ای برای تحلیل عاملی و عوامل خواهیم داشت. البته هر جا احتیاج به محاسبات وجود داشته باشد، برای انجام آن‌ها از کدهایی به زبان پایتون استفاده خواهیم کرد.

تحلیل عاملی

یکی از انواع تحلیل‌های مربوط به «مدل‌های خطی» (Linear Model) در آمار، «تحلیل عاملی» (Factor Analysis) است. با استفاده از تحلیل عاملی، قادر به تفسیر و البته تفکیک واریانس مشاهدات به واریانس عوامل یا متغیرهای پنهان خواهیم بود. متغیرهای قابل مشاهده، متغیرهایی هستند که مقدارهای آن‌ها با توجه به نمونه‌گیری، اندازه‌گیری شده و قابل استفاده هستند. در مقابل، عامل یا متغیرهای پنهان با ترکیب خطی خود متغیرهای قابل مشاهده را می‌سازند.

هر عامل میزان مشخصی از تغییرات یا واریانس کل مدل را توصیف می‌کند. از طرفی متغیرهای پنهان یا عامل‌ها قادر به کاهش ابعاد یک مسئله نیز هستند. در زیر یک مدل تحلیل عاملی برای توصیف تغییرات متغیر $$Y$$ را با استفاده از دو عامل $$F_1$$ و $$F_2$$ را مشاهده می‌کنید. همانطور که دیده می‌شود متغیر قابل مشاهده $$Y$$، توسط ترکیب خطی از این متغیرهای پنهان ایجاد شده است.

$$\large Y_i=\beta_{i0}+\beta_{i1}F_1+\beta_{i2}F_2+e_i$$

رابطه ۱

تحلیل عاملی را می‌توان به صورت تبدیل متغیرهای مربوط به یک مدل از $$X_1,X_2,\cdots, X_l$$ به $$F_1,F_2,\cdots,F_k$$ در نظر گرفت که مسلما مقدار $$k$$ بسیار کوچکتر از $$l$$‌ است. به این معنی که تعداد عامل‌ها از تعداد متغیرهای قابل مشاهده کمتر است. این امر می‌تواند توجیهی برای استفاده از کاهش بُعد در تحلیل عاملی در نظر گرفته شود.

تصویر زیر گویایی چنین ترکیبی است. همانطور که دیده می‌شود متغیرهای قابل مشاهده از نظرسنجی یک رستوران را می‌توان با منشا یک متغیر پنهان به نام «رضایت غیرخوراکی» در نظر گرفت که یک متغیر پنهان است. به عنوان یک متغیر پنهان دیگر با نام «رضایت خوراکی»، می‌توان متغیرهای قابل مشاهده «میزان رضایت از مزه غذا»، «دمای غذای سرو شده»، «تازگی غذا»، را تولید کند. واضح است که «رضایت خوراکی» و «رضایت غیرخوراکی» غیر قابل اندازه‌گیری (پنهان) ولی متغیرهای دیگر مانند «زمان انتظار»، «تمیزی ظروف»، «مزه غذا»، «دمای غذار سرو شده» و ... قابل اندازه‌گیری (قابل مشاهده) هستند.

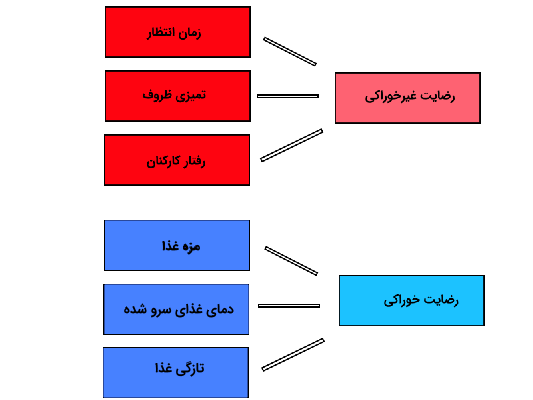
متغیرهای پنهان تولید شده در شکل ۱ می‌توانند به کمک تکنیک تحلیل عاملی ایجاد شوند.

فرضیه‌های اولیه در روش تحلیل عاملی

هنگام استفاده از تحلیل عاملی باید نکاتی که در ادامه به آن اشاره می‌کنیم، رعایت شده باشند. در غیر این صورت ممکن است نتایج حاصل از تحلیل عاملی، قابل اعتماد نباشند.

• داده‌ها نباید شامل مشاهده پرت یا «دورافتاده» (Outlier) باشند.
• اندازه نمونه (Sample Size) باید از تعداد عامل‌ها بیشتر باشد.
• «همخطی کامل» (Perfect Milticollinearity) بین متغیرها وجود نداشته باشد.
• پراکندگی داده‌ها در بین متغیرها نباید یکنواخت باشد. این خاصیت را به نام «یکنواختی» (Homoscedasticity) می‌شناسند. به این ترتیب متغیرها نباید به یک شکل توزیع شده باشند.

انواع روش‌های تحلیل عاملی

روش تحلیل عاملی را به دو شیوه می‌توان پیاده‌سازی کرد. روش «تحلیل عاملی اکتشافی» (Explanatory Factor Analysis) یا EFA که یکی از معمول‌ترین روش‌ها در حوره تحقیقات مدیریتی و علوم اجتماعی محسوب می‌شود. در این شیوه فرض مرتبط بودن یا عامل‌پذیر بودن همه متغیرهای قابل مشاهده در نظر گرفته می‌شود. به این ترتیب هر متغیر قابل مشاهده ترکیب خطی از همه عوامل خواهد بود.

فیلم آموزش نرم‌ افزار لیزرل – مدل‌ سازی معادلات ساختاری SEM با LISREL – مقدماتی در فرادرس

کلیک کنید

روش دیگر که به «تحلیل عاملی تاییدی» (Confirmatory Factor Analysis) یا CFA معروف است، براساس ارتباط بین گروهی از متغیرهای قابل مشاهده با هر عامل استوار است. به این ترتیب مثلا اگر ۲۰ عامل وجود داشته باشد، متغیر قابل مشاهده اول فقط با متغیرهای پنهان ۱ تا ۵ قابل توصیف بوده و متغیر قابل مشاهده ۲ با متغیرهای پنهان یا عامل‌های ۶ تا ۹ و متغیر قابل مشاهده شماره ۳ با متغیرهای پنهان بعدی در ارتباط است. این روش به استخراج عوامل اصلی و پایه‌ای می‌پردازد.

محاسبات در تحلیل عاملی

همانطور که در ابتدای این متن بیان شد، هدف از تحلیل عاملی کاهش متغیرهای قابل مشاهده و تبدیل آن‌ها به متغیرهای پنهان است. این کار را می‌توان در دو گام انجام داد.

• استخراج عوامل‌: در این گام، تعداد عامل‌ها و شیوه استخراج عامل‌ها بوسیله تفکیک واریانس انجام می‌شود. این کار ممکن است بوسیله تحلیل مولفه‌های اصلی یا تحلیل عاملی با واریانس مشترک انجام شود.
• چرخش عامل‌ها: در گام دوم به منظور ایجاد عدم وابستگی (متعامد سازی) بین عامل‌ها، آن‌ها را چرخش می‌دهیم. هدف اصلی برای انجام این کار می‌تواند تفسیرپذیری بهتر عامل‌های ایجاد شده باشد. روش‌های مختلفی برای متعامد سازی عامل‌ها وجود دارد. برای مثال می‌توان به روش‌های چرخش Varimax, Quartimax یا Promax اشاره کرد.

همانطور که قبلا اشاره شد، هر متغیر قابل مشاهده را می‌توان به صورت ترکیب خطی از عوامل تفکیک کرد. عامل شماره یک، متغیر پنهانی است که بیشترین میزان تفکیک واریانس توسط آن صورت گرفته است. از طرفی ممکن است یک یا چند عامل در ترکیب خطی بین متغیرهای قابل مشاهده مشخصی وجود داشته باشند که به این ترتیب واریانس مشترک بین متغیرهای قابل مشاهده توسط عامل‌ها قابل توصیف و تجزیه است.

واضح است که تعداد عامل‌ها حداکثر می‌تواند همان تعداد متغیرهای قابل مشاهده باشد. هر عامل میزان مشخصی از تغییرات یک متغیر قابل مشاهده را نشان می‌دهد. از آنجایی که هدف استفاده از عامل‌ها در یک مسئله مدل‌سازی، کاهش تعداد متغیرها است، در یک تحلیل FA، عامل یا عواملی که کمترین میزان واریانس را برای هر متغیر قابل مشاهده داشته باشند، حذف می‌شوند.

ترکیبی خطی متغیرهای قابل مشاهده برای ایجاد عامل‌ها، دارای ضرایب یا پارامترهایی است که به آن‌ها «بارهای عاملی» (Factor Loading) گفته می‌شود.

نکته: به متغیرهای عامل (Factor) گاهی «متغیر پنهان» (Latent Variable)، متغیر «غیرقابل مشاهده» (Unobserved Variable) و «متغیر فرضیه‌ای» (Hypothetical variable) نیز می‌گویند.

بارهای عاملی

همانطور که گفته شد، بارهای عاملی پارامترهای مدل خطی هستند که رابطه بین متغیرهای قابل مشاهده و عامل‌ها را بیان می‌کند. این پارامترها را می‌توان به صورت یک ماتریس نمایش داد که به آن ماتریس بارها (Loading Matrix) گفته می‌شود. این بارها نمایانگر میزان ارتباط یا همان ضریب همبستگی بین متغیر قابل مشاهده و عامل‌ها است. از طرفی می‌توان میزان واریانس توصیف شده توسط عامل‌ها را برای هر متغیر قابل مشاهده توسط بارهای عاملی تعیین کرد.

مقادیر ویژه ماتریس بارهای عاملی

مقادیر ویژه (Eigen Value) مربوط به ماتریس بارهای عاملی، بیانگر میزان واریانس یا پراکندگی است که هر عامل نسبت به متغیر قابل مشاهده بیان می‌کند. گاهی این مقادیر ویژه را ریشه‌های معادله مشخصه نیز می‌نامند.

مقادیر مشترک (Commonalities)

واریانس مشترک یا مقادیر مشترک، مجموع مربعات بارهای عاملی برای هر متغیر قابل مشاهده است. این مقدار همان سهمی یا درصدی است که یک عامل از واریانس متغیر قابل مشاهده با دیگر عامل‌ها به اشتراک گذاشته است. مقدار سهم واریانس مشترک می‌توان بین صفر تا یک تغییر کند. مقادیر نزدیک به ۱ نشانگر سهم بیشتر در بیان واریانس توسط هر عامل‌ است. بنابراین اگر فرض کنید ۵ متغیر قابل مشاهده داشته باشیم، و ضریب عامل $$j$$ام برای آن‌ها به صورت $$L_{ij}$$ باشد، مقدار مشترک یا واریانس مشترک توسط عامل $$j$$ام به صورت زیر خواهد بود.

$$\large h_{j}=\sum_{i=1}^l L_{ij}$$

رابطه ۲

مشخص است که در اینجا $$l$$ همان تعداد متغیرهای قابل مشاهده است. در این صورت $$h_j$$ میزان یا سهم عامل $$j$$ام از واریانس کل است.

تعیین تعداد عامل‌ها

با توجه به تعداد عامل‌هایی که سهم بیشتری از واریانس کل را بیان می‌کنند، می‌توان تعداد عامل‌های مناسب را انتخاب کرد. در روشی که به نام «معیار کایسر» (Kaiser) معروف است، مقادیر ویژه ماتریس بارها، محاسبه شده و تغییرات مقدارهای ویژه رصد می‌شوند. زمانی که این تغییرات قابل اغماض باشد، تعداد عامل‌ها شناسایی می‌شوند. در تصویر زیر نموداری به نام نمودار scree plot‌ یا نمودار قطعه‌ای را مشاهده می‌کنید که در آن سه عامل با بزرگترین مقدارها ویژه انتخاب شده‌اند، زیرا تغییرات مقدارهای ویژه از سومین عامل به بعد محسوس نیست.

تحلیل عاملی و مقایسه آن با تحلیل مولفه‌های اصلی

در ادامه به طور فهرست‌وار تحلیل عاملی را با تحلیل مولفه‌‌های اصلی مقایسه کرده‌ایم. واضح است در تحلیل عاملی، واریانس مشترک باعث ایجاد عامل‌ها شده در حالیکه در تحلیل مولفه‌ای، واریانس کل بین مولفه‌ها تقسیم خواهد شد.

• در تحلیل مولفه‌های اصلی (PCA)، در بین مولفه‌های تولید شده، اولین مولفه بیشترین میزان واریانس را توصیف می‌کند و به ترتیب مولفه‌های بعدی با توجه به تفکیک واریانس، سهم‌های کوچکتری نسبت به مولفه اول خواهند داشت. در حالیکه در تحلیل عاملی (FA)، توصیف ماتریس کوواریانس برای داده‌ها صورت می‌گیرد و میزان پراکندگی مشترکی (کوواریانس) که بین عوامل وجود دارد استخراج می‌شود.
• مولفه‌های حاصل از PCA بر یکدیگر عمودند و به نوعی می‌توان مولفه‌ها را مستقل از یکدیگر در نظر گرفت. در حالیکه در تحلیل FA لزومی به عمود بودن عوامل بر یکدیگر وجود ندارد.
• هر یک از مولفه‌ها در تحلیل PCA ترکیبی خطی از متغیرهای قابل مشاهده هستند. در حالیکه در تحلیل FA، متغیرهای قابل مشاهده، ترکیبی خطی از متغیرهای پنهان یا غیرقابل مشاهده هستند.
• مولفه‌های اصلی حاصل از PCA قابل تفسیر یا نام‌گذاری نیستند. در حالیکه عامل‌های ساخته شده توسط روش FA را می‌توان به خوبی تفسیر و نام‌گذاری کرد.
• تحلیل مولفه‌های اصلی، روشی برای کاهش بعد با استفاده از مولفه‌هایی است که بیشترین پراکندگی را بیان می‌کنند. تحلیل عاملی برای تولید متغیرهای پنهان به کار می‌رود.
• شاید بتوان PCA را نوع خاصی از تحلیل FA نامید. PCA کار روی متغیرهای قابل مشاهده است در حالیکه هدف از FA مدل‌سازی است.

برای مقایسه بهتر بین این دو تکنیک به تصویر زیر توجه کنید. مشخص است که پراکندگی کل داخل کادر قرار گرفته است. رنگ‌ها نقش مولفه‌ها یا عامل‌ها را در بیان پراکندگی کل نشان می‌دهند.

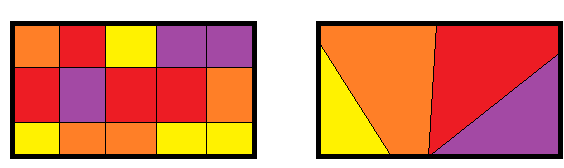
در تصویر سمت چپ، تکنیک FA به کار رفته و مولفه‌های با رنگ مشابه، عامل‌هایی هستند که دارای واریانس مشترک هستند. به این ترتیب رنگ‌های قرمز تشکیل یک عامل و رنگ‌های زرد، عامل دیگر و ... خواهند بود. در مقابل تکنیک PCA کل واریانس را بین مولفه‌ها تفکیک می‌کند و هر مولفه سهمی از واریانس کل دارد که در تصویر سمت راست دیده می‌شود. البته در هر دو تصویر از چهار مولفه استفاده شده است. همانطور که مشخص است، در تصویر سمت چپ، مجموع مساحت مربوط به هر رنگ با مساحت همان رنگ در تصویر سمت راست مطابقت دارد.

تحلیل مولفه‌های اصلی در پایتون با بسته factor_analyzer

در این قسمت، به منظور انجام محاسبات و اجرای تحلیل عاملی روی یک مجموعه داده، از زبان برنامه‌نویسی پایتون و کتابخانه مرتبط با تحلیل عاملی استفاده می‌کنیم. ابتدا بسته یا کتابخانه‌های مربوطه را معرفی و بارگذاری می‌کنیم.

فیلم آموزش اسمارت پی ال اس SmartPLS برای مدلسازی معادلات ساختاری و تحلیل آماری در مقاله و پایان نامه در فرادرس

کلیک کنید

کتابخانه‌های مورد نیاز

برای بارگذاری کتابخانه‌های مرتبط با تحلیل عاملی از کد زیر استفاده شده است. مشخص است که تابع pd از pandas و load_iris از sklearn.datasets و FactorAnalyzer از factor_analyzer و plt نیز از matplotlib.pyolot فرخوانی و بارگذاری شده‌اند.

1# Import required libraries
2import pandas as pd
3from sklearn.datasets import load_iris
4from factor_analyzer import FactorAnalyzer
5import matplotlib.pyplot as plt

بارگذاری داده‌ها

به منظور انجام تحلیل عاملی از داده‌های مربوط به پروژه ارزیابی شخصیت (personality assessment project) به نام BFI استفاده کرده‌ایم. این مجموعه داده را می‌توانید از (+) دریافت کنید. در این مجموعه داده ویژگی‌های شخصیتی با مقیاسی در شش سطح، مورد ارزیابی قرار گرفته‌اند. طیف و سطوح این متغیرها به صورت زیر است.

البته متغیر‌های دیگری مانند سن، میزان تحصیلات، جنسیت نیز در این مجموعه داده وجود دارد. کد زیر به منظور بارگذاری این مجموعه داده در پایتون نوشته شده است.

1df= pd.read_csv("bfi.csv")

برای نمایش اسامی متغیرها (ستون‌های مجموعه داده) از دستور زیر استفاده کنید.

1df.columns

خروجی در این حالت به صورت زیر خواهد بود.

1Index(['A1', 'A2', 'A3', 'A4', 'A5', 'C1', 'C2', 'C3', 'C4', 'C5', 'E1', 'E2',
2       'E3', 'E4', 'E5', 'N1', 'N2', 'N3', 'N4', 'N5', 'O1', 'O2', 'O3', 'O4',
3       'O5', 'gender', 'education', 'age'],
4      dtype='object')

در گام بعدی متغیرهای جنسیت (gender)، تحصیلات (education) و سن (age) را از مجموعه داده خارج کرده‌ایم. همچنین «مقدارهایی گمشده» (Missings) که با na‌ یا null مشخص شده‌اند برای تحلیل در مدل در نظر گرفته نمی‌شوند.

1# Dropping unnecessary columns
2df.drop(['gender', 'education', 'age'],axis=1,inplace=True)
3
4# Dropping missing values rows
5df.dropna(inplace=True)
6df.info()

نتیجه حاصل از این عملیات در ادامه قابل مشاهده است.

1<class 'pandas.core.frame.DataFrame'>
2Int64Index: 2436 entries, 0 to 2799
3Data columns (total 25 columns):
4A1    2436 non-null float64
5A2    2436 non-null float64
6A3    2436 non-null float64
7A4    2436 non-null float64
8A5    2436 non-null float64
9C1    2436 non-null float64
10C2    2436 non-null float64
11C3    2436 non-null float64
12C4    2436 non-null float64
13C5    2436 non-null float64
14E1    2436 non-null float64
15E2    2436 non-null float64
16E3    2436 non-null float64
17E4    2436 non-null float64
18E5    2436 non-null float64
19N1    2436 non-null float64
20N2    2436 non-null float64
21N3    2436 non-null float64
22N4    2436 non-null float64
23N5    2436 non-null float64
24O1    2436 non-null float64
25O2    2436 non-null int64
26O3    2436 non-null float64
27O4    2436 non-null float64
28O5    2436 non-null float64
29dtypes: float64(24), int64(1)
30memory usage: 494.8 KB

به کمک دستور زیر چند سطر اول از محاسبات صورت گرفته ظاهر خواهد شد.

1df.head()

همانطور که می‌بینید فقط متغیرهای مربوط به ارزیابی شخصیت در تحلیل به کار خواهند رفت که به شکل یک ماتریس با ۲۵ ستون خواهند بود. توجه دارید که در پایتون اولین اندیس با صفر آغاز می‌شود به همین دلیل شماره مشاهدات از صفر ظاهر شده است.

آزمون کفایت

قبل از اجرای تحلیل عاملی باید شرط‌ مربوط به عامل‌پذیری را بررسی کنیم. با این کار به این سوال پاسخ خواهیم داد که آیا متغیرهای مربوط به مجموعه داده قادر به تولید عوامل می‌باشند؟ برای پاسخ به این سوال می‌توان به کمک دو روش عمل کرد. اولین روش استفاده از «آزمون بارتلت» (Bartlett’s Test) و دومین روش «آزمون کایزر-مایر-اولکین» (Kaiser-Meyer-Olkin Test) است. در ادامه با هر یک از این روش‌‌ها آشنا خواهیم شد.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

آزمون بارتلت

«آزمون بارتبلت» (Bartlett's Test) یک آزمون به منظور بررسی وجود رابطه کُروی بین متغیرها است. به این ترتیب اگر متغیرها به یکدیگر وابستگی نداشته باشند و ماتریس همبستگی برابر با «ماتریس یکه» (Identical Matrix) باشد، فرض صفر که یکه بودن ماتریس همبستگی در آزمون بارتلت است رد نخواهد شد. در صورت رد شدن فرض صفر، عامل‌پذیری متغیرهای مجموعه داده مورد تایید قرار خواهد گرفت. کد زیر به منظور اجرای این آزمون برای مجموعه داده مورد نظر نوشته شده است. این تابع از کتابخانه factor_analyzer قابل استفاده است.

1from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
2chi_square_value,p_value=calculate_bartlett_sphericity(df)
3chi_square_value, p_value

همانطور که در ادامه نتیجه اجرای این برنامه و خروجی آزمون بارتلت را مشاهده می‌کنید، اولین رقم مقدار آماره بارتلت و دومین مقدار همان p-value مربوط به این آزمون است. واضح است که مقدار p-value حدود صفر شده (با یک رقم اعشار) که بیانگر یکه نبودن ماتریس همبستگی است. بنابراین متغیرهای این مجموعه داده، عامل‌پذیر هستند.

1(18146.065577234807, 0.0)

آزمون کایزر-مایر-اولکین (KMO)

همانطور که آزمون بارتلت نشان داد، متغیرهای قابل مشاهده در مجموعه داده قابلیت ایجاد عامل را دارند ولی در اینجا شاخص KMO یا (Kaiser-Meyer-Olkin) را محاسبه می‌کنیم تا باز هم عامل‌پذیری مجموعه داده را مورد بررسی قرار دهیم. در ادامه قطعه کدی را می‌بینید که به منظور استخراج شاخص KMO‌ برای این مجموعه داده لازم است. واضح است که این کار توسط تابع calculate_kmi از کتابخانه factor.analyzer صورت گرفته است.

1from factor_analyzer.factor_analyzer import calculate_kmo
2kmo_all,kmo_model=calculate_kmo(df)
3kmo_model

حاصل اجرای این برنامه مقدار شاخص عامل‌پذیری KMO‌ است. هر چه این مقدار به یک نزدیک باشد، بیانگر عامل‌پذیری بیشتر مجموعه داده‌ها است.

10.8486452309468382

مقدار KMO برای این داده‌ها حدود  0.84 است که به نظر بسیار خوب می‌رسد و حاکی از عامل‌پذیری زیاد در این مجموعه داده است. پس بهتر است کار استخراج عامل‌ها را ادامه دهیم.

تعیین تعداد عامل‌ها

به منظور انتخاب تعداد عامل‌ها از کد زیر استفاده کرده‌ایم. ابتدا مقدارهای ویژه یا بارهای عاملی بدون دوران (Rotation) یا گردش را استخراج کرده‌ایم. سپس برحسب این مقادیر، نمودار قطعه‌ای (Scree plot) را ترسیم خواهیم کرد.

1# Create factor analysis object and perform factor analysis
2fa = FactorAnalyzer()
3fa.analyze(df, 25, rotation=None)
4# Check Eigenvalues
5ev, v = fa.get_eigenvalues()
6ev

نتیجه اجرای این کد به صورت زیر خواهد بود.

کدی که در ادامه می‌بینید به منظور ترسیم نمودار قطعه‌ای ایجاد شده است. محور افقی در این نمودار تعداد عامل‌ها و محور عمودی نیز مقدارهای ویژه را نشان می‌دهد. در ادامه فقط شش مقدار ویژه که از بین بزرگترین مقدارها استخراج شده‌اند، قابل مشاهده است. به این ترتیب به نظر می رسد که احتیاج به شش عامل یا متغیر پنهان خواهیم داشت.

1# Create scree plot using matplotlib
2plt.scatter(range(1,df.shape[1]+1),ev)
3plt.plot(range(1,df.shape[1]+1),ev)
4plt.title('Scree Plot')
5plt.xlabel('Factors')
6plt.ylabel('Eigenvalue')
7plt.grid()
8plt.show()

نمودار قطعه‌ای را در این تصویر مشاهده می‌کنید به «نمودار بازویی» (Elbow Plot) نیز معروف است.

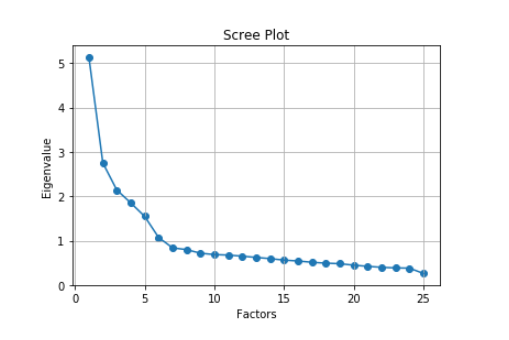
مشخص است که در این نمودار به ازای هر مقدار ویژه، خط افقی ترسیم شده و زمانی که نمودار در حدود یک خط افقی تغییرات محسوسی نداشته باشد، محل شکست روی محور افقی تعداد عامل‌ها را مشخص می‌کند. توسط نمودار بالا شش عامل اول انتخاب شده است.

1# Create factor analysis object and perform factor analysis
2fa = FactorAnalyzer()
3fa.analyze(df, 6, rotation="varimax")
4
5fa.loadings

همانطور که دیده می‌شود عامل اول، با بزرگترین بارهای عاملی برای متغیرهای $$E1$$ تا $$E5$$ استخراج شده است. در فهرست زیر این عامل‌ها معرفی شده‌اند. واضح است که به نظر می‌رسد این عامل‌ها با گروه خاصی از متغیرهای قابل مشاهده در ارتباط هستند در نتیجه مدل تحلیل عاملی از نوع تاییدی (Confirmatory Factor Analysis - CFA) است. با توجه به مسئله مورد نظر که مرتبط با شناخت شخصیت است، عامل‌ها را می‌توان مطابق با آنچه در ادامه مشاهده می‌شود، نام‌گذاری کرد.

• عامل اول: در ترکیب خطی با متغیرهای $$E1,E2 \cdots, E5$$ وجود دارد زیرا بزرگترین مقدار ویژه یا بار عاملی را با این متغیرها دارد. به نظر می‌رسد که این عامل را باید «برونگرایی» (Extraversion) نامید.
• عامل دوم: در ترکیب خطی با متغیرهای $$N1,N2,\cdots,N5$$ به کار رفته است زیرا بزرگترین مقدار ویژه یا بار عاملی را با این متغیرها دارد. شاید بهتر باشد این عامل را «شاخص‌های سلامت روانی» (Neuroticism) نامید.
• عامل سوم هم در ترکیب خطی با متغیرهای $$C1,C2,\cdots,C5$$ قرار دارد زیرا بزرگترین مقدار ویژه یا بار عاملی را با این متغیرها دارد. شاید بهتر باشد که این عامل را «وفاداری» (Conscientiousness) نام‌گذاری کرد.
• عامل چهارم هم در ترکیب خطی با متغیرهای $$O1,O2,\cdots,O5$$ قرار دارد که دارای بزرگترین مقدار ویژه با این متغیرها را دارد. شاید بتوان این عامل را «قابلیت پذیرش» (Openness) نامید.
• عامل پنجم هم با متغیرهای قابل مشاهده $$A1,A2,\cdots, A5$$ در ترکیب خطی ظاهر می‌شود زیرا بزرگترین مقدار ویژه را با این متغیرها خواهد داشت. شاید بتوان این عامل را «توافق‌پذیری» (Agreeableness) نامید.
• در انتها نیز عامل ششم را نمی‌توان ترکیب خطی قوی با متغیرهای دیگر در نظر گرفت. شاید بهتر باشد که آن را حذف کنیم و با پنج عامل کار را ادامه دهیم.

نکته: منظور از بزرگی ضریب یا بار عاملی، قدر مطلق مقدار مورد نظر است. به همین علت مثلا برای متغیر $$A1$$ عامل پنجم در نظر گرفته شد زیرا بار عاملی آن قدر مطلق بزرگتری نسبت به قدر مطلق بارهای عامل دیگر دارد.

کد زیر به بررسی تحلیل عامل براساس ۵ عامل اول پرداخته است.

1# Create factor analysis object and perform factor analysis using 5 factors
2fa = FactorAnalyzer()
3fa.analyze(df, 5, rotation="varimax")
4fa.loadings

مشخص است که در این حالت بارها تغییر یافته و مدل متفاوتی از حالت قبلی ایجاد می‌شود. کدی که در ادامه مشاهده می‌کنید سهم هر یک از عامل‌ها را با توجه به رابطه ۲ محاسبه می‌کند.

1# Get variance of each factors
2fa.get_factor_variance()

با توجه به سطر آخر این جدول که سهم تجمعی هر عامل از بیان واریانس را مشخص می‌کند، واضح است که حدود ۴۲٪ واریانس کل توسط ۵ عامل با بزرگترین مقادیر ویژه، تعیین شده است.

نکاتی در مورد به کارگیری تحلیل عاملی

بوسیله تحلیل عاملی می‌توانیم اطلاعات زیادی را در مورد وابستگی بین متغیرها کشف کنیم. تعداد متغیرهای قابل مشاهده در مدل بوسیله تکنیک FA کاهش می‌یابد و همچنین گروهی از متغیرهایی مرتبط با یکدیگر به شناسایی شده که از ترکیب خطی آن‌ها برای ایجاد مدل استفاده می‌شود.

فیلم آموزش تجزیه و تحلیل اطلاعات با نرم افزار SAS ساس در فرادرس

کلیک کنید

این کار به شناسایی متغیرهای پنهان بخصوص در مدل‌های تصادفی در حوزه تحقیقات بازار کمک شایانی می‌کند. این‌ها همه مزایای به کارگیری تحلیل عاملی محسوب می‌شوند ولی بعضی از معایب تحلیل عاملی نیز در ادامه تذکر داده شده‌اند.

• نتایج حاصل از تحلیل عاملی ممکن است بسیار بحث‌برانگیز باشد.
• تفسیر خروجی‌های تحلیل عاملی نیز ممکن است براساس حتی یک مجموعه داده متفاوت باشد زیرا نام‌گذاری و تعیین ویژگی حاصل تولید شده براساس تحلیل عاملی بسیار به تجربه و شناخت موضوع مورد تحلیل وابسته است.

خلاصه و نتیجه‌‌گیری

در این نوشتار با تحلیل عاملی و شیوه‌های گوناگون پیاده‌سازی آن آشنا شدیم. روند و مراحل اجرای تحلیل عاملی نیز از مواردی بود که در این متن به آن پرداخته شد. همچنین تعیین تعداد عامل‌های مناسب در مدل نیز مورد بحث قرار گرفت و مقایسه‌ای نیز بین تحلیل عاملی و تحلیل مولفه‌های اصلی صورت گرفت. در هر قسمت کدهایی نیز به زبان پایتون برای روشن‌تر شدن موضوع ارائه گردید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات
• آموزش همبستگی و رگرسیون خطی در SPSS
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های برنامه‌نویسی پایتون
• ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• رگرسیون غیر خطی در R — به زبان ساده
• توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده

^^