تحلیل سری زمانی با پایتون — مقدمات و مفاهیم اولیه

تحلیل سری زمانی، مرتبط با داده‌هایی است که به نحوی با زمان در ارتباط هستند. تشخیص رفتار و بخصوص پیش‌بینی این داده‌ها از مباحث مربوط به سری زمانی است. در این نوشتار به بررسی روش‌های تحلیل سری زمانی با پایتون خواهیم پرداخت. تحلیل سری زمانی با پایتون به صورت دنباله‌ای از نوشتارها در سه بخش ارائه می‌شود.

• بخش نخست: تحلیل سری زمانی با پایتون --- مقدمات و مفاهیم اولیه
• بخش دوم: تحلیل سری زمانی با پایتون --- معرفی انواع مدل‌ها
• بخش سوم: تحلیل سری زمانی با پایتون --- مدل‌های ترکیبی و پیچیده

برای آشنایی بیشتر با مقدمات مربوط به مبحث سری زمانی بهتر است نوشتار تحلیل سری زمانی — تعریف و مفاهیم اولیه را بخوانید. همچنین خواندن مطلب سری زمانی در علم داده — از صفر تا صد نیز خالی از لطف نیست.

تحلیل سری زمانی

تحلیل سری‌های زمانی در بسیاری از زمینه‌ها بخصوص صنعت کسب و کار و بنگاه‌های مالی گرفته تا علوم اجتماعی به کار می‌رود. از آنجایی که رفتار داده‌ها در بستر زمان یکسان نیست، الگو‌ها و شیوه‌های مختلفی برای پیش‌بینی سری‌های زمانی ابداع و تعریف شده است. در این نوشتار به معرفی بعضی از این الگو‌ها خواهیم پرداخت و شیوه‌های به کارگیری هر یک را شرح خواهیم داد. از طرفی برای پیاده‌سازی محاسبات روی داده‌های سری زمانی از زبان برنامه‌نویسی و محاسباتی پایتون استفاده خواهیم کرد. به این ترتیب با استفاده از داده‌های جمع‌آوری شده درباره یک پدیده اجتماعی، مالی، صنعتی، گذشته را چراغ راه آینده خواهیم کرد.

فیلم آموزش تحلیل سری های زمانی با پایتون و آر R در فرادرس

کلیک کنید

برای شروع بهتر است کتابخانه مورد نیاز در پایتون را بارگذاری کنیم. دستورات زیر به این منظور تهیه شده است.

1import os
2import sys
3
4import pandas as pd
5import pandas_datareader.data as web
6import numpy as np
7
8import statsmodels.formula.api as smf
9import statsmodels.tsa.api as smt
10import statsmodels.api as sm
11import scipy.stats as scs
12from arch import arch_model
13
14import matplotlib.pyplot as plt
15import matplotlib as mpl
16%matplotlib inline
17p = print
18
19p('Machine: {} {}\n'.format(os.uname().sysname,os.uname().machine))
20p(sys.version)

در ادامه نیز برای بارگذاری داده‌های مالی سایت یاهو (Yahoo.com) دستوراتی معرفی شده‌ است که برای مراحل بعدی اجرای آن‌ها ضروری است. با اجرای کدهای زیر به کمک بسته pandas_datareader داده‌های مربوطه دریافت می‌شوند.

1end = '2015-01-01'
2start = '2007-01-01'
3get_px = lambda x: web.DataReader(x, 'yahoo', start=start, end=end)['Adj Close']
4
5symbols = ['SPY','TLT','MSFT']
6# raw adjusted close prices
7data = pd.DataFrame({sym:get_px(sym) for sym in symbols})
8# log returns
9lrets = np.log(data/data.shift(1)).dropna()

سری زمانی ایستا و ناایستا

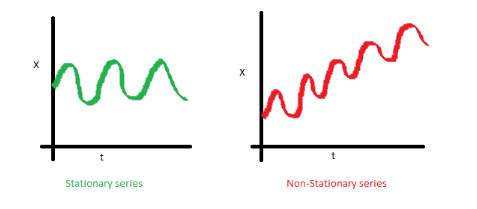
به تصویرهای زیر توجه کنید. در همه آن‌ها محور افقی بیانگر زمان و محور عمودی متغیری است که وابسته به زمان تغییر می‌کند. این متغیر می‌تواند میزان بارش، حرارت، درآمد و غیره باشد. مطمئن هستیم که تغییرات این متغیر وابسته به زمان است و قرار است مقدار آن را برای زمان آینده پیش‌بینی کنیم. سری زمانی که با رنگ سبز نشان داده است، سری ایستا و در مقابل سری زمانی قرمز رنگ، بیانگر سری زمانی ناایستا است. در ادامه به بررسی عواملی می‌پردازیم که یک سری زمانی را ناایستا می‌کنند.

روند (Trend)

اگر میانگین سری زمانی وابسته به زمان نباشد، آن را «سری زمانی ایستا» (Stationary Time Series) می‌نامیم. در این صورت تغییرات میانگین سری زمانی برحسب زمان باعث «ناایستایی سری زمانی» (Non-Stationary Time Series) خواهد شد. تغییرات میانگین در طول دوره یا بازه زمانی سری را «روند» (Trend) می‌نامند. ممکن است الگوی تغییرات به صورت صعودی یا نزولی باشد.

ثابت بودن واریانس

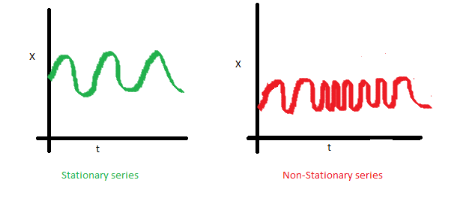
اگر واریانس پدیده سری زمانی در طول زمان ثابت نباشد، باز هم سری را ناایستا می‌نامند. در سری زمانی ایستا، پراکندگی یا واریانس نباید تابعی از زمان محسوب شود. این خاصیت را گاهی «یکنواختی» (Homoscedasticity) می‌نامند. در تصویر زیر به خوبی نابرابری واریانس در بازه‌های مختلف زمانی در نمودار قرمز رنگ دیده می‌شود. در حالیکه در نمودار سبز رنگ، میزان تغییرات یکسان به نظر می‌رسد. توجه داشته باشید که منظور از واریانس میانگین مربعات نوسانات نسبت به خط مرکزی روی محور عمودی است.

یکنواختی در واحدهای زمانی

برای اینکه نشان دهیم میزان تغییرات سری زمانی در طول‌های مشخصی از زمان نیز مستقل از زمان است، از مفهوم کوواریانس کمک می‌گیریم. در یک سری زمانی ایستا، در بازه‌های زمانی به طول m (یعنی فاصله زمانی i تا i+m) داده‌های سری نباید وابسته به زمان باشند. در تصویر زیر، نمودار قرمز رنگ، نشانگر عدم چنین خاصیتی است، پس سری زمانی با توجه به اینکه دارای واریانس و میانگین ثابتی است، باز هم سری زمانی ایستا نخواهد بود.

ولی شاید این سوال به ذهن برسد که چرا سری زمانی باید ایستا باشد؟ آیا برای سری‌های زمانی ناایستا نمی‌توان تحلیل مناسبی انجام داد و به پیش‌بینی دقیقی رسید؟ با توجه به اینکه بسیاری از پدیده‌های مرتبط با سری زمانی ایستا نیستند، چگونه تحلیل سری زمانی روی آن‌ها صورت خواهد گرفت؟

علت اصلی تحلیل سری زمانی روی داده‌های زمانی ایستا، سادگی انجام محاسبات است. از طرفی وجود چنین خاصیتی امکان برآورد شاخص‌های دیگر مانند میانگین و واریانس و ... را فراهم می‌آورد. به علاوه روش‌های دقیق و مناسبی برای ایستا کردن سری‌های زمانی ناایستا نیز وجود دارد. بنابراین با توجه به این موضوعات ابتدا روش‌های تحلیل سری زمانی ایستا را مورد بررسی قرار داده، سپس به سری‌های زمانی ناایستا خواهیم پرداخت.

ضریب همبستگی دنباله‌ای

هنگام ایجاد یک مدل سری زمانی، رفتار سری زمانی را می‌توان معمولا به سه بخش تقسیم کرد. روند (Trend)، تغییرات فصلی یا تناوبی (Seasonal/Cyclic) و تغییرات تصادفی. قسمت تصادفی در حقیقت میزان خطای مدل را نشان می‌دهد که توسط اختلاف مقدار واقعی سری با مقدار پیش‌بینی محاسبه می‌شود. ضریب خودهمبستگی میزان ارتباط بین مقدارهای خطا در مدل سری را نشان می‌دهد. از آنجایی که ضریب خودهمبستگی، می‌تواند معیاری برای سنجش صحت مدل سری زمانی محسوب شود، محاسبه آن ضروری به نظر می‌رسد. با توجه به مباحت و مسائل تئوری، می‌دانیم باید مقدارهای خطا مستقل از یکدیگر باشند. پس یکی از شرط‌های مناسب بودن مدل آن است که خودهمبستگی برابر با صفر باشد.

فیلم آموزش تبدیل لگاریتمی و تفاضل گیری در پیش پردازش سری های زمانی (رایگان) در فرادرس

کلیک کنید

نویز-نوفه (Noise) و قدم‌های تصادفی (Random Walk)

اولین و ساده‌ترین مدل برای داده‌های سری زمانی، مدل «نویز سفید» (White Noise) یا «نوفه» است که به مدل خطای تصادفی نرمال نیز مشهور است. براساس تعریف، مدل نوفه یا نویز سفید، دنباله‌ای از مقدارهای وابسته به زمان هستند که به یکدیگر مرتبط یا وابستگی ندارند بطوری که میانگین مقدارها برابر با صفر است. در چنین حالتی، جملات خطاها را می‌توان «مستقل و هم‌توزیع» (Independent and Identically Distributed - iid) در نظر گرفت. به این ترتیب عدم وابستگی مقدارهای خطا تضمین می‌شود. این موضوع بسیار اهمیت دارد زیرا اگر مدل سری زمانی به درستی تحلیل و ساخته شود، انتظار داریم خطاها تصادفی بوده و iid باشند. به این ترتیب خطاها را به صورت «نویز سفید» (White Noise) می‌شناسیم.

در این مرحله می‌خواهیم یک فرآیند نوفه را شبیه‌سازی کنیم. در ادامه با استفاده از کد زیر، تابعی برای ترسیم نمودار سری زمانی به همراه تحلیل خودهمبستگی معرفی کرده‌ایم.

1def tsplot(y, lags=None, figsize=(10, 8), style='bmh'):
2    if not isinstance(y, pd.Series):
3        y = pd.Series(y)
4    with plt.style.context(style):    
5        fig = plt.figure(figsize=figsize)
6        #mpl.rcParams['font.family'] = 'Ubuntu Mono'
7        layout = (3, 2)
8        ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
9        acf_ax = plt.subplot2grid(layout, (1, 0))
10        pacf_ax = plt.subplot2grid(layout, (1, 1))
11        qq_ax = plt.subplot2grid(layout, (2, 0))
12        pp_ax = plt.subplot2grid(layout, (2, 1))
13        
14        y.plot(ax=ts_ax)
15        ts_ax.set_title('Time Series Analysis Plots')
16        smt.graphics.plot_acf(y, lags=lags, ax=acf_ax, alpha=0.5)
17        smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax, alpha=0.5)
18        sm.qqplot(y, line='s', ax=qq_ax)
19        qq_ax.set_title('QQ Plot')        
20        scs.probplot(y, sparams=(y.mean(), y.std()), plot=pp_ax)
21
22        plt.tight_layout()
23    return

حال به کمک دستورات زیر یک دنباله از اعداد تصادفی (۱۰۰۰ مشاهده) با توزیع نرمال تولید کرده و به عنوان نویز سفید در نظر می‌گیریم. سپس به کمک تابعی که در قسمت قبل معرفی شد، نمودارهای مربوط به تحلیل سری زمانی نوفه را رسم می‌کنیم.

1np.random.seed(1)
2
3# plot of discrete white noise
4randser = np.random.normal(size=1000)
5tsplot(randser, lags=30)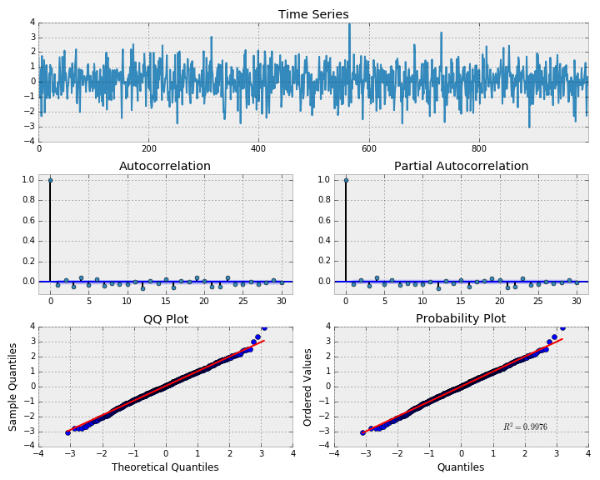

براساس این نمودارها، متوجه می‌شویم که میانگین این فرآیند تصادفی (سری زمانی) صفر است. نمودار ACF (خودهمبستگی-Autocorrelation) و PCAF (خودهمبستگی جزئی-Partial Autocorrelation) نیز نشان می‌دهند، بین داده‌ها ارتباطی وجود ندارد به این معنی که براساس نمودارهایی که در ردیف دوم قرار دارند، نقطه‌ها بسیار به صفر نزدیک هستند.

در انتها نیز نمودار چندکی (Q-Q plot) که مقایسه بین چندک‌های توزیع نرمال و توزیع داده‌ها را نشان می‌دهد، تایید کننده نرمال بودن داده‌ها است. همچنین نمودار احتمال (Probability Plot) نیز بر همین مسئله تاکید دارد.

نکته: البته باید توجه داشت که داده‌های تصادفی تولید شده دارای توزیع نرمال بودند و باید این نمودارها نیز بیانگر نرمال بودن توزیع داده‌ها باشند.

به منظور مشاهده مقدار شاخص‌های آماری توزیع این داده‌ها، (مانند میانگین-mean، واریانس-Variance و انحراف استاندارد-Standard Deviation) دستور زیر را اجرا کنید.

1p("Random Series\n -------------\nmean: {:.3f}\nvariance: {:.3f}\nstandard deviation: {:.3f}"
2.format(randser.mean(), randser.var(), randser.std()))
3
4# Random Series
5# -------------
6# mean: 0.039 
7# variance: 0.962
8# standard deviation: 0.981

همانطور که در خطوط انتهایی خروجی مشاهده می‌کنید شاخص‌های آماری محاسبه و نمایش داده شده‌اند. این مقدارها نشان می‌دهند که میانگین نزدیک به صفر و واریانس نیز نزدیک به ۱ بدست آمده‌اند که از خصوصیات اصلی نویز سفید یا نوفه محسوب می‌شود.

«قدم‌های تصادفی» (Random Walk) نیز به صورت یک سری زمانی با نماد $$x_t$$ تعریف می‌شود که مدل آن با نگاه ریاضی به شکل زیر نوشته می‌شود.

$$\large x_t=x_{t-1}+w_t$$

در این رابطه مشخص است که در زمان $$t$$ مقدار سری به مقدار گذشته آن یعنی $$x_{t-1}$$ وابسته است. از طرفی جمله $$w_t$$ نیز یک سری زمانی نویز سفید یا نوفه است. از خصوصیات مهم قدم‌های تصادفی، ناایستا بودن است زیرا کوواریانس در بازه‌ها زمانی وابسته به زمان است. به این ترتیب اگر سری زمانی مطابق با مدل قدم‌های تصادفی باشد، امکان پیش‌بینی آن وجود ندارد.

در ادامه به شبیه‌سازی فرآیند قدم‌های تصادفی به کمک کدهای برنامه‌نویسی پایتون می‌پردازیم. همانطور که مشخص است دستور np.random.normal برای ایجاد نوفه‌ها استفاده شده است. کدهای زیر به منظور شبیه‌سازی ۱۰۰۰ مشاهده از قدم‌های تصادفی ایجاد شده است. رابطه‌ای که برای تولید سری زمانی با قدم‌های تصادفی معرفی شد در کدها درون یک حلقه for قرار گرفته است.

1# Random Walk without a drift
2
3np.random.seed(1)
4n_samples = 1000
5
6x = w = np.random.normal(size=n_samples)
7for t in range(n_samples):
8    x[t] = x[t-1] + w[t]
9
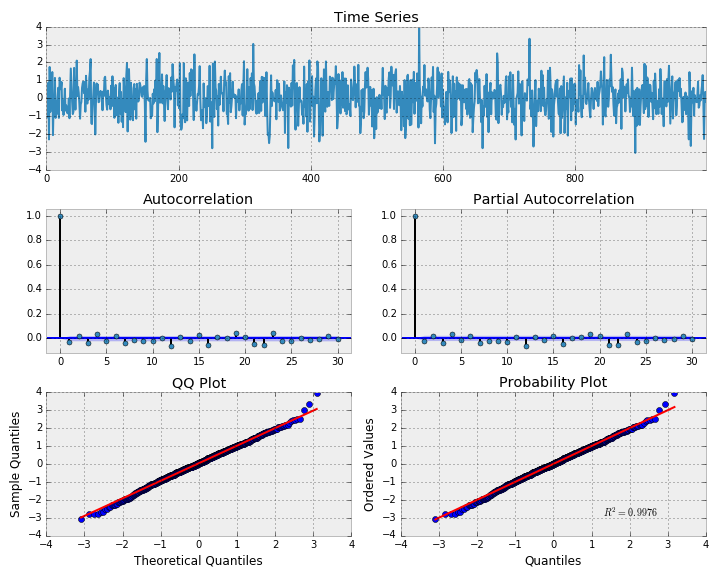
10_ = tsplot(x, lags=30)

با توجه به خط آخر کد ارائه شده، نمودارهای مربوط به تحلیل سری‌زمانی که قبلا معرفی کردیم، ایجاد خواهد شد.

همانطور که در نمودار ACF دیده می‌شود، ناهمبستگی در بین مشاهدات دیده نمی‌شود. از طرفی نمودارهای P-P plot و Q-Q plot نیز نرمال بودن داده‌ها را تایید نمی‌کنند. اجازه دهید مدل ارائه شده را به شکلی تغییر دهیم تا نرمال بودن جمله خطا ($$w_t$$) مورد بررسی قرار گیرد. با تغییر رابطه بالا به صورت زیر می‌توانیم این بررسی را انجام دهیم.

$$\large x_t-x_{t-1}=w_t$$

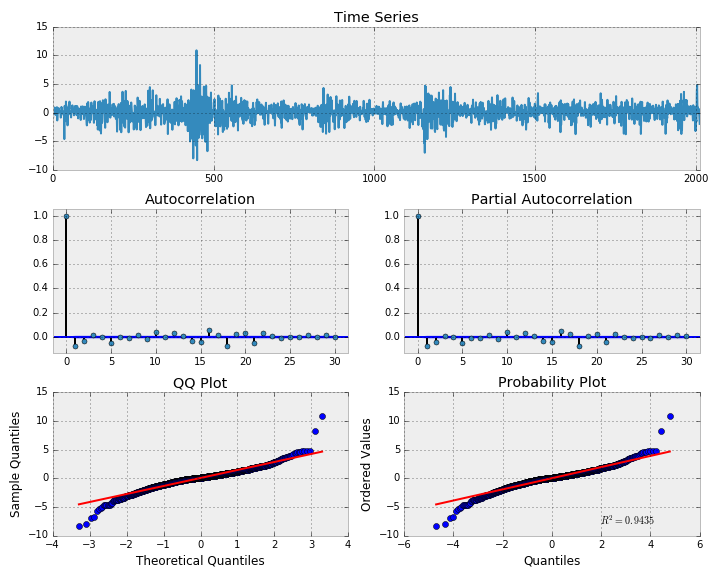
بر این اساس، تفاضل مرتبه اول سری زمانی برابر با نویز سفید خواهد بود. در کد زیر برای انجام این محاسبات و رسم نمودارهای تحلیل سری زمانی از تابع np.diff از کتابخانه nampy استفاده کرده‌ایم.

1# First difference of simulated Random Walk series
2
3_ = tsplot(np.diff(x), lags=30)

با اجرای دستور بالا، خروجی‌ها به صورت زیر ظاهر خواهند شد. در اینجا به وضوح ایستا بودن سری زمانی تفاضلی (نویز سفید) دیده می‌شود. مقدار ACF و PACF حدود صفر بوده و توزیع داده‌ها براساس نمودارهای P-P plot و Q-Q plot نیز نرمال است.

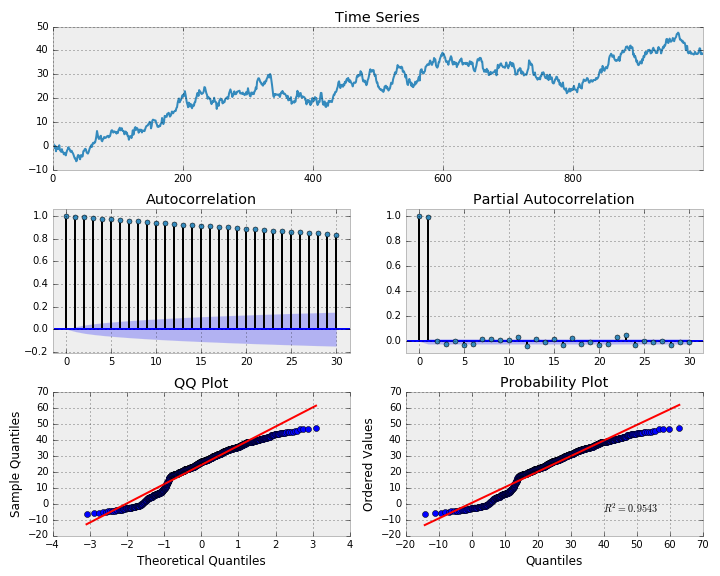
بر همین اساس، برای داده‌های data.SPY که در ابتدا متن توسط کد‌هایی از سایت یاهو بارگذاری شد، عمل تفاضل‌گیری مرتبه اول اجرا و نمودارهای تجزیه و تحلیل سری‌زمان توسط دستور زیر ترسیم می‌شود.

1# First difference of SPY prices
2_ = tsplot(np.diff(data.SPY), lags=30)

نکته: در تابع tsplot مقدار lags یا تاخیرها برابر با ۳۰ انتخاب شده تا نشان‌دهنده تاخیرهای ماهانه یا ۳۰ روز باشد.

با شگفتی متوجه می‌شویم که سری به نظر ایستا می‌آید. با توجه به نمودارهای Q-Q plot و P-P plot نرمال بودن داده‌ها مشخص است ولی به نظر می رسد که دم‌های توزیع نرمال کمی کشیده‌تر (Heavy Tail) است. از طرفی مقدار ACF و PACF در نقطه‌های (تاخیرات) ۱، ۵، ۱۶ ، ۱۸ و ۲۱ صفر نیستند که مشخص کننده وجود مدل مناسب‌تر برای چنین داده‌هایی است. در ادامه بررسی این داده‌ها و تعیین مدل مناسب‌تر خواهیم پرداخت.

مدل خطی (Linear Model)

اگر بتوان مدل سری زمانی را به صورت معادله یک خط برحسب زمان نشان داد، به آن «مدل خطی سری زمانی» (Time Series Linear Model) گفته می‌شود.

فیلم آموزش مانایی، ریشه واحد و هم انباشتگی در تحلیل و پیش بینی سری های زمانی (رایگان) در فرادرس

کلیک کنید

معمولا از چنین مدلی برای بیان تغییرات سری زمانی همراه با «روند» (Trend) استفاده می‌شود. شکل رابطه ریاضی برای چنین مدلی به صورت زیر است.

$$\large y_t=b_0+b_1t+\varepsilon_t$$

در این مدل، مقدارهای متغیر وابسته ($$y_t$$) به صورت ترکیبی خطی از زمان با ضرایب $$b_0, b_1$$ نوشته شده‌اند. البته در انتها نیز جمله خطا (نویز سفید) نیز قرار دارد که آن هم برای زمان $$t$$ مقداری متفاوت خواهد داشت. از مشخصه‌های اصلی این مدل عدم وابستگی ضرایب مدل خطی یعنی $$b_0, b_1$$ به زمان است. برای مثال می‌توان میزان فروش یک شرکت که به صورت صعودی رو به افزایش است را با چنین مدلی از سری زمانی تحلیل کرد. در ادامه به شبیه‌سازی چنین داده‌های پرداخته‌ایم. مقدار $$b_0=-50$$ انتخاب شده و نشانگر عرض از مبدا است. همچنین ضریب متغیر زمان نیز که شیب خط را مشخص می‌کند $$b_1=25$$ در نظر گرفته شده است.

1# simulate linear trend
2# example Firm ABC sales are -$50 by default and +$25 at every time step
3
4w = np.random.randn(100)
5y = np.empty_like(w)
6
7b0 = -50.
8b1 = 25.
9for t in range(len(w)):
10    y[t] = b0 + b1*t + w[t]
11    
12_ = tsplot(y, lags=lags)

به منظور بررسی وضعیت سری زمانی شبیه‌سازی شده، تابع مربوط به رسم نمودارهای تحلیل سری زمانی را نیز در خط آخر کد فراخوانی کرده‌ایم. در نمودار اول، رابطه بین متغیر زمان و متغیر وابسته به صورت کاملا خطی دیده می‌شود.

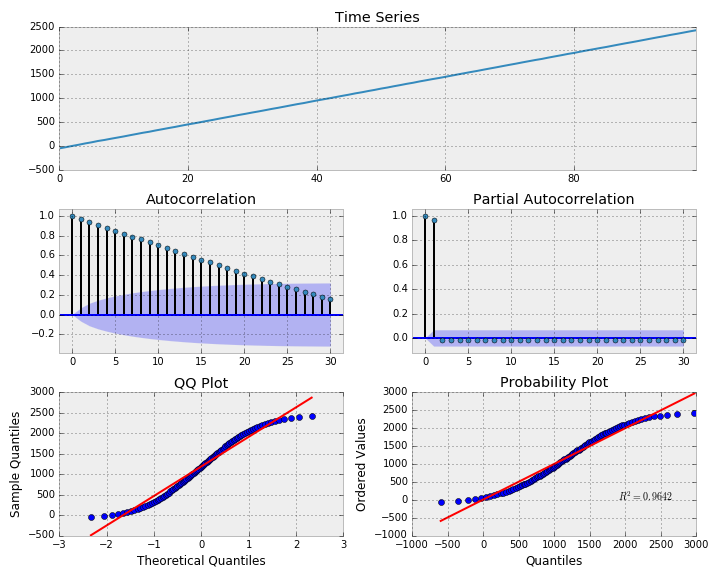
توسط نمودار ACF، می‌توان دید که باقی‌مانده‌های مدل، همبستگی داشته و به صورت یک خط نزولی نسبت به تاخیرات (Lag) دیده می‌شود. ضریب همبستگی جزئی نیز بعد از تاخیرات ۱، به صفر رسیده‌اند. همچنین نرمال بودن باقی‌مانده توسط نمودارهای Q-Q plot و P-P plot تقریبا تایید می‌شوند.

برای پیش‌بینی چنین سری زمانی باید آن را به حالت ایستا درآورد تا نتایج پیش‌بینی صحت داشته باشند.

مدل لگاریتم خطی (Log-Linear Model)

این مدل درست به مانند مدل خطی است با این تفاوت که داده‌ها به صورت یک تابع نمایی هستند بطوری که نرخ تغییرات در هر بازه زمانی ثابت است و لگاریتم آن‌ها بیانگر یک تابع خطی خواهد بود.

برای مثال فرض کنید یک شرکت بازرگانی به نام ABC، در هر دوره زمانی به میزان x درصد رشد در فروش داشته است. هنگام ترسیم چنین داده‌های نمودار به صورت نمایی خواهد بود. در ادامه کدی که به منظور شبیه‌سازی چنین داده‌هایی به کار رفته، مشاهده می‌شود.

1# Simulate ABC exponential growth
2
3# fake dates
4idx = pd.date_range('2007-01-01', '2012-01-01', freq='M')
5
6# fake sales increasing at exponential rate
7sales = [np.exp( x/12 ) for x in range(1, len(idx)+1)]
8
9# create dataframe and plot
10df = pd.DataFrame(sales, columns=['Sales'], index=idx)
11
12with plt.style.context('bmh'):
13    df.plot()
14    plt.title('ABC Sales')

به نمودار زیر که بیانگر یک تابع نمایی است توجه کنید.

همانطور که گفته شد اگر از چنین داده‌هایی لگاریتم طبیعی گرفته شود، رابطه خطی شده و نمودار به صورت یک خط راست در خواهد آمد. این کار را با دستور زیر اجرا کرده‌ایم.

1# ABC log sales 
2
3with plt.style.context('bmh'):
4    pd.Series(np.log(sales), index=idx).plot()
5    plt.title('ABC Log Sales')

همانطور که در نمودار زیر می‌بنید یک خط راست برای نمایش رابطه بین تغییرات لگاریتم داده‌ها برحسب زمان ترسیم شده است.

همانطور که دیده می‌شود، این مدل نمی‌تواند مبنای مناسبی برای پیش‌بینی سری زمانی باشد زیرا کاملا مشخص است که خطاها ناهمبسته نیستند و همانطور که در مدل خطی نیز اشاره شد مدل ایستا نبوده و نیاز است که از مدل‌های دیگری برای پیش‌بینی استفاده شود.

نکته: همانطور که تا به حال دیده شد، شرایط ایستایی در مدل‌هایی که معرفی کردیم وجود نداشت ولی انتظار داریم به کمک تبدیلاتی مثل «تفاضل‌گیری» (Difference) آن‌ها را ایستا کنیم.

در قسمت‌های دوم و سوم از این دنباله مقالات، به بررسی مدل‌هایی می‌پردازیم که ایستا هستند. سپس برای سری‌های زمانی ناایستا به دنبال تبدیلاتی هستیم که آن‌ها را تبدیل به مدل‌هایی ایستا کند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌بینی و تحلیل سری‌های زمانی
• آموزش تحلیل و پیش‌بینی سری های زمانی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های کاربردی شبکه های عصبی مصنوعی
• سری زمانی در علم داده — از صفر تا صد
• تحلیل سری زمانی — تعریف و مفاهیم اولیه

^^