تابع هارمونیک — به زبان ساده (+ دانلود فیلم آموزش رایگان)
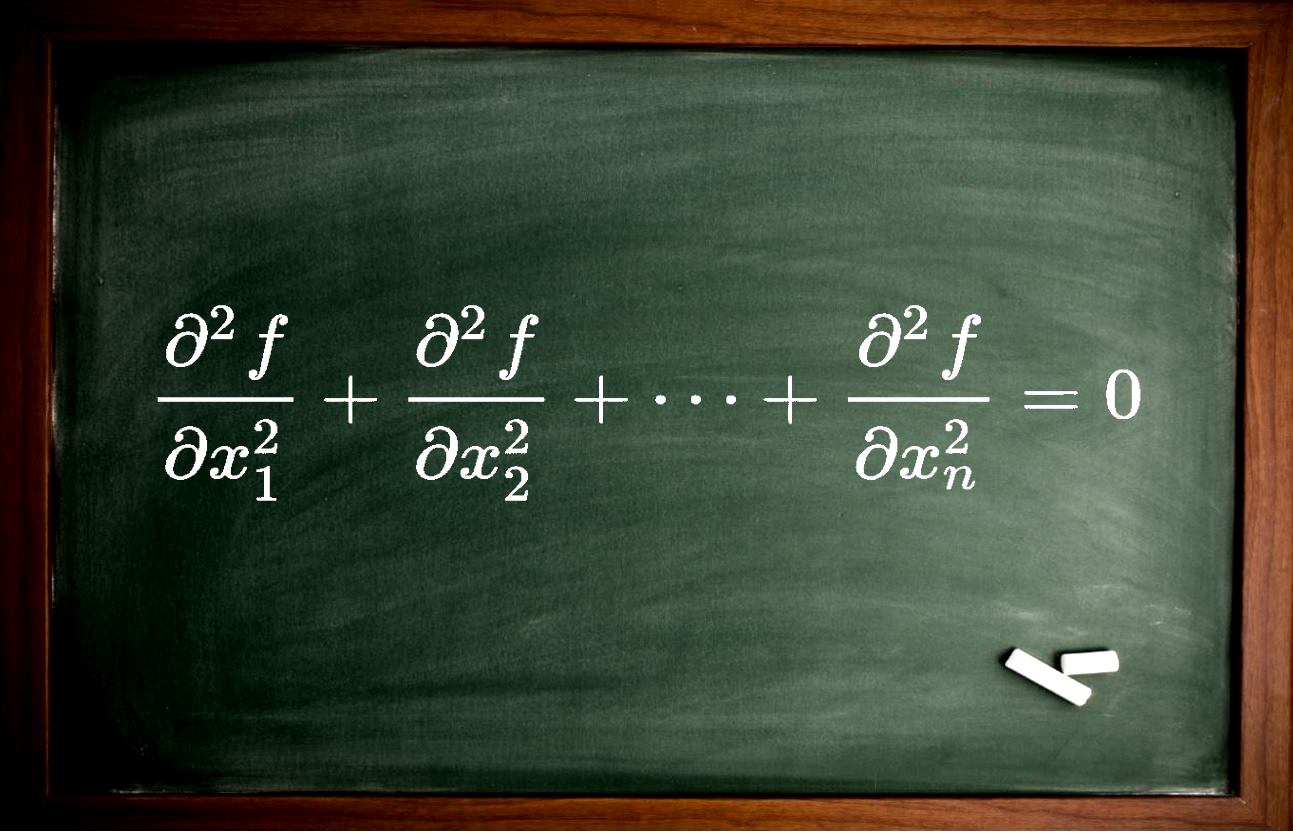
تابع هارمونیک نوعی خاص از توابع چندمتغیره محسوب میشود که در آنالیز مختلط و مسائل مهندسی و فیزیک کاربرد بسیاری دارد. البته پیشنهاد میشود به منظور درک بهتر این مطلب، در ابتدا مطلب تابع مختلط را مطالعه فرمایید.
فیلم آموزشی تابع هارمونیک
تابع هارمونیک
تعریف: یک تابع دومتغیره همچون $$ u ( x , y ) $$، زمانی هارمونیک تلقی میشود که دوبار مشتقپذیر بوده و معادله دیفرانسیل با مشتقات جزئی زیر را ارضا کند.
$$ \nabla ^ { 2 } u = u _ { x x } + u _ { y y } = 0 $$
به عبارت فوق معادله لاپلاس گفته میشود. بنابراین زمانی تابع $$ u $$ هارمونیک است که معادله لاپلاس را ارضا کند. اوپراتور $$ \nabla ^ { 2 } $$ تحت عنوان لاپلاسین شناخته شده و به $$ \nabla ^ { 2 } u $$ لاپلاسینِ $$ u $$ گفته میشود.
اوپراتور دِل ($$ \large \nabla $$)
اوپراتور دل، برداری است که از یک تابع در جهات مختلف مشتقگیری میکند. با فرض $$ F = ( u , v ) $$ میتوان گزارههای زیر را در مورد این اوپراتور بیان کرد:
- $$ \nabla = \left( \frac { \partial } { \partial x } , \frac { \partial } { \partial y } \right ) $$
- $$ \nabla u = \left( u _ { x } , u _ { y } \right ) $$
- $$ \operatorname {curl} \mathbf { F } = \boldsymbol { \nabla } \times \mathbf { F } = \left( v _ { x } - u _ { y } \right) \mathbf { k } $$
- $$ \operatorname {div} \mathbf { F } = \nabla \cdot \mathbf { F } = u _ { x } + v _ { y } $$
- $$ \operatorname {div} \operatorname {grad} u = \nabla \cdot \nabla u = \nabla ^ { 2 } u = u _ { x x } + u _ { y y } $$
تابع تحلیلی
ارتباط کاملا واضح و روشنی میان تابع تحلیلی و تابع هارمونیک وجود دارد. در بسیاری از موارد میتوان این ارتباط را همچون ارتباط بین دو تابع $$ e ^ z $$ و $$ \sin $$ یا $$ \cos $$ دانست. به منظور درک بهتر مقدار مختلط $$ z $$ و تابع $$ f ( z ) $$ را به صورت زیر در نظر بگیرید.
$$ z = x + i y $$
$$ f ( z ) = u ( x , y ) + i v ( x , y ) $$
قضیه: اگر تابع $$ f ( z ) = u ( x , y ) + i v ( x , y ) $$ روی ناحیه $$ A $$ تحلیلی باشد، در این صورت هر دو تابع $$ u , v $$ روی این ناحیه، تابع هارمونیک محسوب میشوند.
اثبات: با توجه به معادله کوشی ریمان (با توجه به فرض تحلیلی بودن تابع $$ f $$)، برای یک تابع تحلیلی رابطه بین بخشهای حقیقی و موهومی آن به صورت زیر است.
$$ u _ { x } = v _ { y } $$
با مشتقگیری دوباره نسبت به $$ x $$ داریم:
$$ u _ { x x } = v _ { y x } $$
به طور مشابه با مشتقگیری از $$ u _ { y } = - v _ { x } $$ نسبت به $$ y $$، عبارتِ $$ u _ { y y } = - v _ { x y } $$ بدست میآید. حال با توجه به $$ u _ { x x } = v _ { y x } $$ میتوان عبارت زیر را بیان کرد:
$$ u _ { x x } + u _ { y y } = v _ { y x } - v _ { x y } = 0 $$
بنابراین همانطور که اثبات شد تابع تحلیلی $$ u $$ در معادله لاپلاس صدق میکند (به طور مشابه همین کار را میتوان برای $$ v $$ نیز انجام داد). در نتیجه $$ u $$ یک تابع هارمونیک محسوب میشود. البته قضیه فوق را میتوان به صورتی عکس نیز بیان کرد.
قضیه: اگر $$ u ( x , y ) $$ روی ناحیهای همچون $$ A $$ هارمونیک باشد، در این صورت $$ u $$ را میتوان بخش حقیقی تابع $$ f ( z ) = u ( x , y ) + i v ( x , y ) $$ در نظر گرفت.
در بیانی دیگر معمولا بخشهای $$ u , v $$ تابعی تحلیلی همچون $$ f ( z ) = u + i v $$ را هارمونیک مزدوج نیز مینامند.
اصل ماکزیمم و مقدار میانگین
اگر $$ u $$ تابعی هارمونیک باشد، در این صورت تابع $$ u $$ ویژگی مقدار میانگین را دارد. برای توضیح ویژگی مقدار میانگین، فرض کنید $$ u $$ تابعی هارمونیک در دایرهای به شعاع $$ r $$ و به مرکز $$ z _ { 0 } = x _ { 0 } + i y _ { 0 } $$ باشد. در این صورت مقدار $$ u \left( x _ { 0 } , y _ { 0 } \right) $$ را میتوان با استفاده از انتگرال زیر بدست آورد.
$$ u \left( x _ { 0 } , y _ { 0 } \right) = \frac { 1 } { 2 \pi } \int _ { 0 } ^ { 2 \pi } u \left( z _ { 0 } + r \mathrm { e } ^ { i \theta } \right ) d \theta $$
تعامد
یکی از مهمترین ویژگیهای $$ u , v $$ در یک تابع تحلیلی، متعامد بودن آنها است. به طور دقیقتر میتوان گفت اگر $$ z = x + i y $$ و $$ f ( z ) = u ( x , y ) + i v ( x , y ) $$ باشد، در این صورت حاصل ضرب داخلی زیر را میتوان نوشت.
$$ \nabla u \cdot \nabla v = 0 $$
اثبات ضرب فوق را میتوان به راحتی و با استفاده از معادله کوشی-ریمان انجام داد. به منظور اثبات میتوان گفت:
$$ \nabla u \cdot \nabla v=\left( u _ { x } , u _ { y } \right) \cdot\left( v _ { x } , v _ { y } \right) = u _ { x } v _ { x } + u _ { y } v _ { y } = v _ { y } v _ { x } - v _ { x } v _ { y } = 0 $$
توجه داشته باشید که در قدم آخر، به جای $$ v _ y $$ از $$ u _ x $$ و به جای $$ - v _ x $$ از $$ u _ y $$ استفاده شده است.
مثال ۱
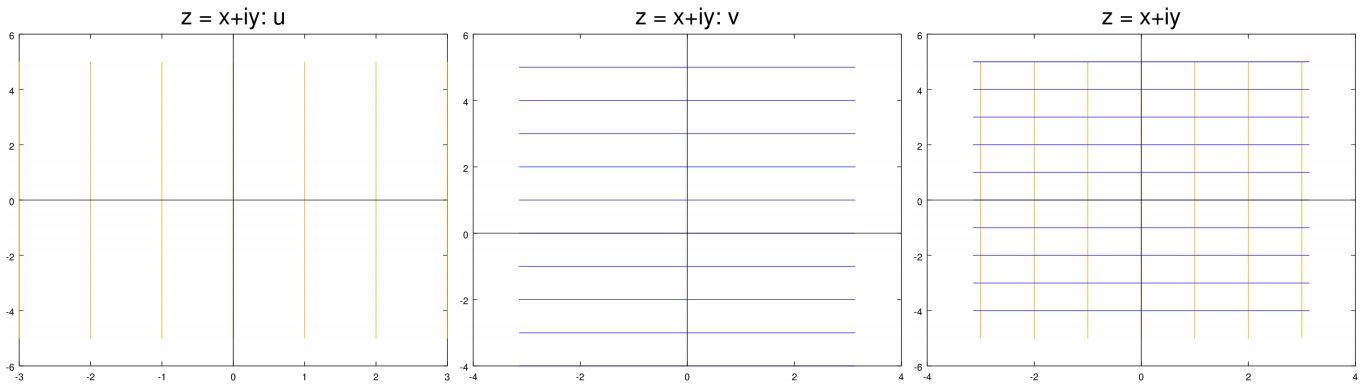
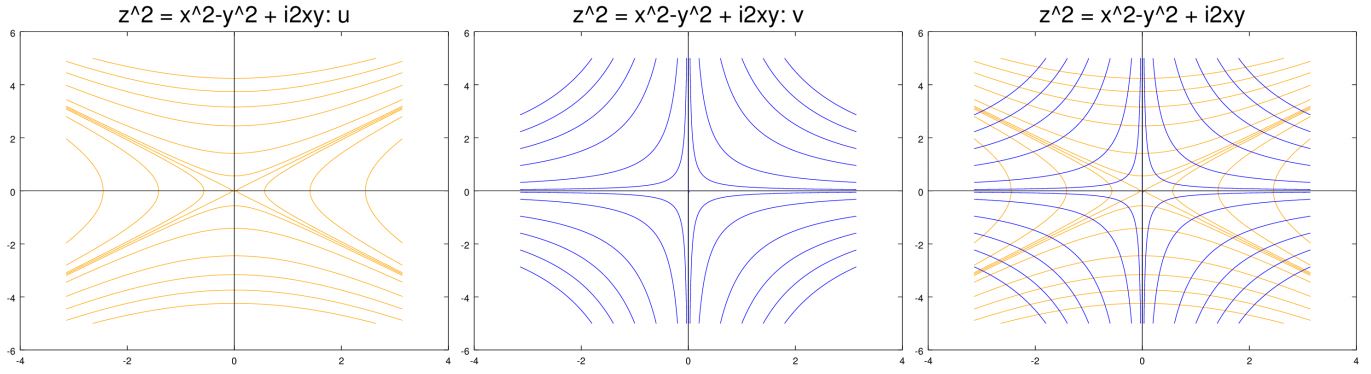
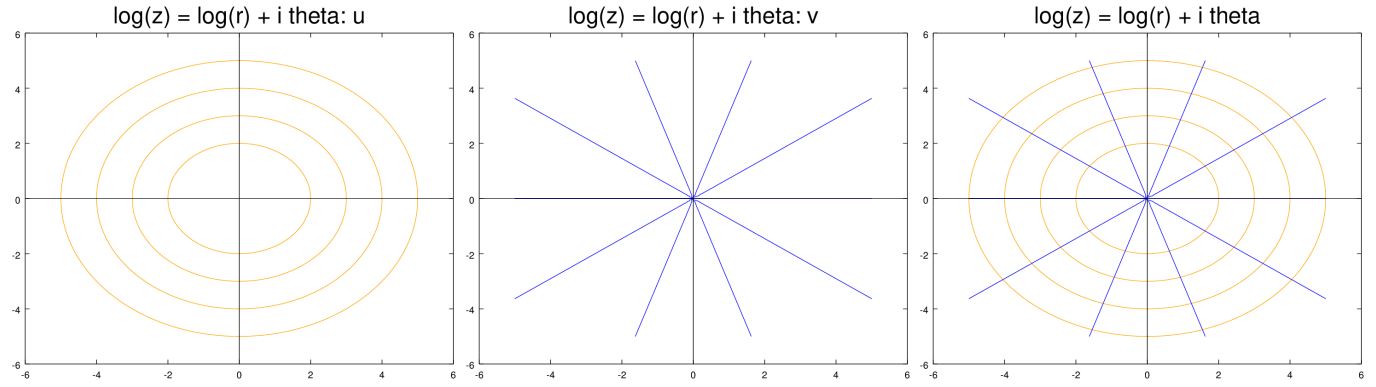
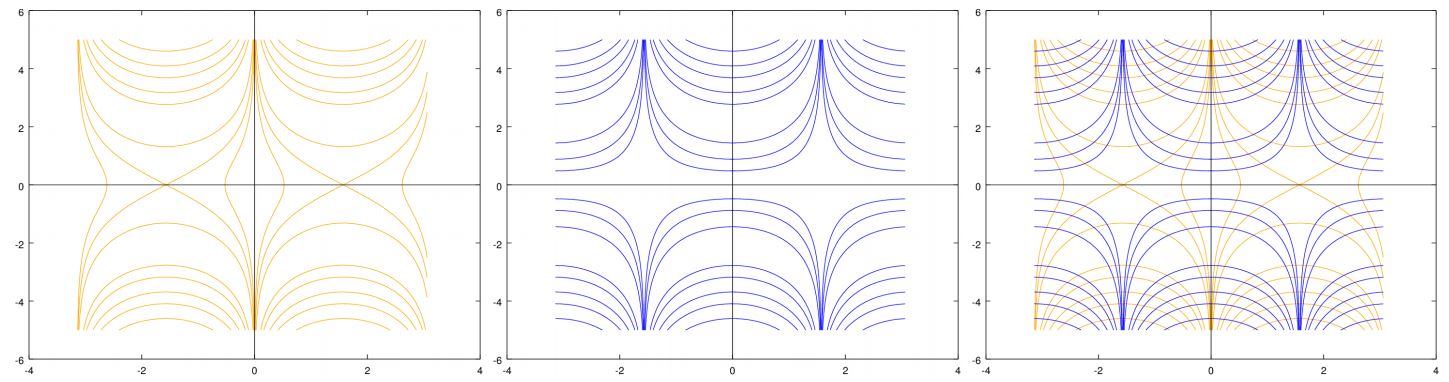
در شکل زیر خطوط $$ u , v $$ مربوط به سه تابع مختلف نشان داده شدهاند. همانطور که مشاهده میکنید خطوط بخشهای حقیقی ($$ u $$) و موهومی ($$ v $$) به هم عمود هستند. خطوط زرد رنگ نشاندهنده بخش حقیقی و خطوط آبی نشاندهنده بخش موهومی هستند. شکل سمت راست نیز هر دوی این خطوط را با هم نشان میدهد.
در شکل زیر نیز بخشهای حقیقی و موهومی تابع زیر ترسیم شدهاند.
$$ f ( z ) = \sin ( x ) \cosh ( y ) + i \cos ( x ) \sinh ( y ) + i \ \sin ( z ) = \sin ( x ) \cosh ( y ) + i \cos ( x ) \sinh ( y ) $$
مثال ۲
تابع زیر را در نظر بگیرید.
$$ f ( z ) = z ^ { 2 } = \left ( x ^ { 2 } - y ^ { 2 } \right) + i 2 x y $$
گرادیان بخشهای حقیقی و موهومی این تابع برابرند با:
$$ \nabla u = ( 2 x , - 2 y ) \text { , } \nabla v = ( 2 y , 2 x ) $$
حال با محاسبه ضرب داخلی دو گرادیان فوق، مقدار صفر بدست میآید. بنابراین همانطور که مشاهده خطوط این دو تابع هارمونیک به یکدیگر عمود هستند. در نتیجه برای این تابع میتوان گفت:
$$ \nabla u \cdot \nabla v = 0 $$
روند فوق را میتوان برای تابع $$ f ( z ) = \frac { 1 } { z } = \frac { x } { r ^ { 2 } } - i \frac { y } { r ^ { 2 } } $$ نیز انجام داد.
$$ \nabla u = \left( \frac { y ^ { 2 } - x ^ { 2 } } { r ^ { 4 } } , \frac { - 2 x y } { r ^ { 4 } } \right) \text { and } \nabla v = \left( \frac { 2 x y } { r ^ { 4 } } , \frac { y ^ { 2 } - x ^ { 2 } } { r ^ { 4 } } \right) $$
$$ \Rightarrow \nabla u \cdot \nabla v = 0 $$
در صورتی که مطلب فوق برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^











بسیار عالی ممنون از مجموعه خوبتون
یک سوال دارم
برای یک سیستم دوجزیی که غلظت آن ثابت است،ثابت کنید که:
Dab=Dba