معادله لاپلاس — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

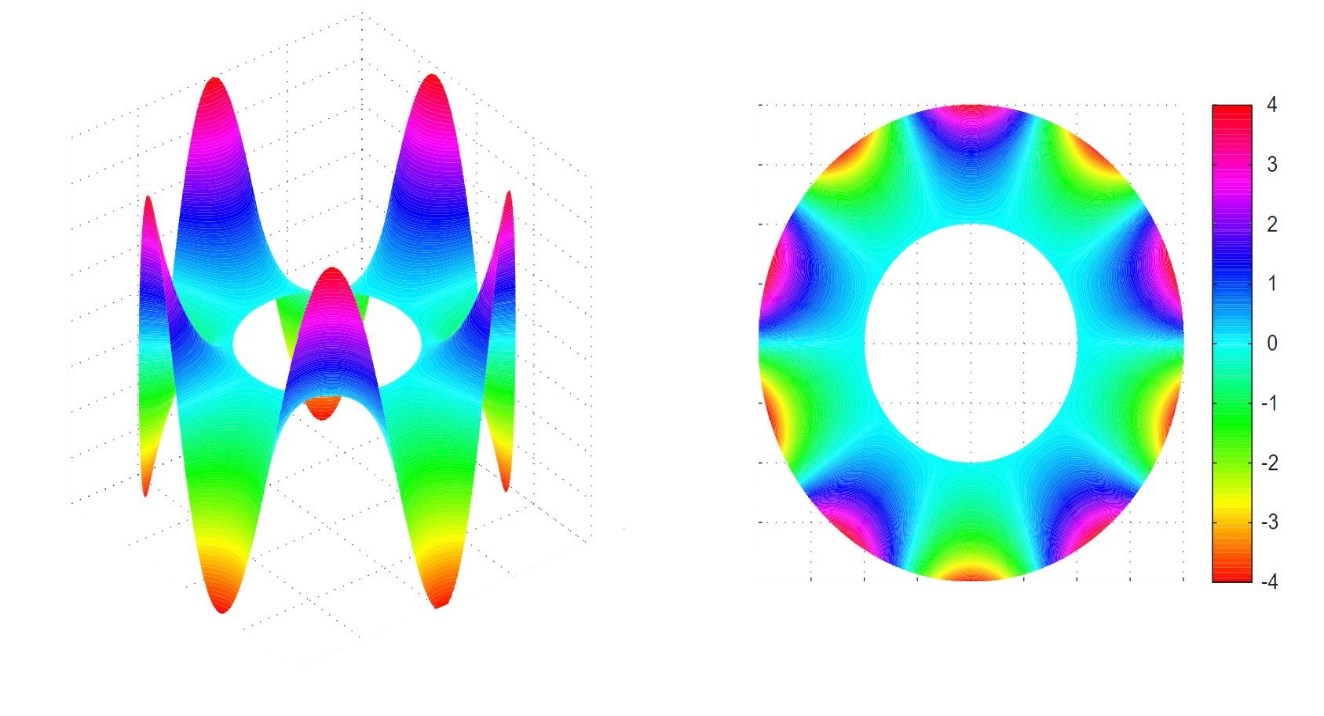
معادله لاپلاس در ریاضیات، به معادله دیفرانسیلی مرتبه دوم اطلاق می‌شود که شکل آن به‌صورت زیر باشد.

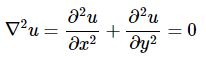
البته توجه داشته باشید که رابطه بالا در حالت دوبعدی نوشته شده است. نمونه‌ای از کاربرد فیزیکی معادله لاپلاس در انتقال حرارت است. در حقیقت رابطه انتقال حرارت در حالت دوبعدی به‌صورت زیر است.

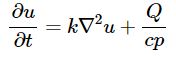
در رابطه فوق u همان دما است. اگر منبع حرارتی (Q=0) و تغییرات زمانی دما برابر با صفر باشد ($${\partial u \over {\partial t}}=0$$)، رابطه بالا به شکل معادله لاپلاس در خواهد آمد. قبل از مطالعه ادامه مطلب پیشنهاد می‌کنیم حتما مطلب روش جداسازی متغیر‌ها در حل معادلات با مشتقات جزئی مطالعه شود.

پاسخ‌های معادله لاپلاس

با توجه به درجه دو بودن و دو متغیره بودن معادله لاپلاس، نیاز به ۴ شرط مرزی داریم (البته توجه داشته باشید که در حالت سه‌بعدی به ۶ شرط مرزی نیاز داریم). فرض کنید می‌خواهیم معادله انتقال حرارت را روی صفحه‌ای مستطیلی مطابق با شکل زیر، با ۴ شرط مرزی حل کنیم.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

بنابراین هدف ما پیدا کردن تابع دمای (u(x,y بر حسب متغیر‌های x و y است.

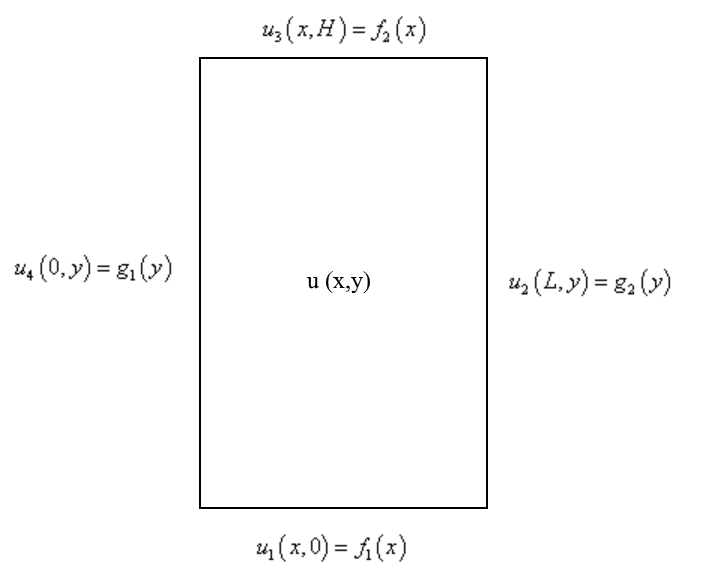
دمای سمت راست و چپ صفحه را برابر با توابع g و دمای بالا و پایین را برابر با توابع f در نظر بگیرید. در نتیجه معادله لاپلاس مربوط به صفحه فوق و شرایط مرزی آن برابرند با:

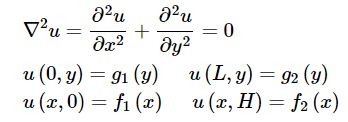
توجه داشته باشید که معادله، خطی و همگن اما شرایط مرزی، خطی و غیرهمگن است. غیر همگن بودن شرایط مرزی، حل مسئله را اندکی با مشکل مواجه می‌کند چرا که دیگر نمی‌توان از روش جداسازی متغیر‌ها استفاده کرد. جهت حل مسئله بالا با استفاده از جداسازی متغیر‌ها، می‌توان در ۴ حالت جداگانه مسئله را حل کرد و نهایتا پاسخ‌های مرتبط با هرکدام از آن‌ها را با یکدیگر جمع کرد. این ۴ حالت در اشکال زیر نشان داده شده‌اند.

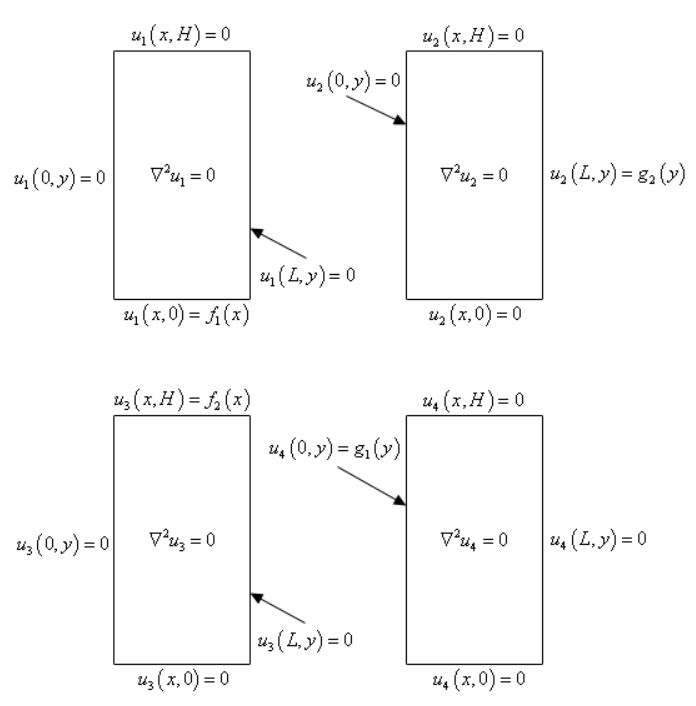
اگر پاسخ هرکدام از حالات بالا، به‌صورت جداگانه برابر با u_i باشد (u₁ ,u₂ ,u₃ ,u₄)، پاسخ نهایی مسئله برابر است با:

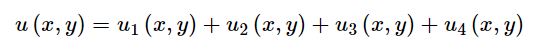
هرکدام از u‌ها را می‌توان با روش ارائه شده در مثال زیر حل کرد. در مثال‌ ارائه شده، از روش‌ جداسازی متغیر‌ها جهت حل معادله لاپلاس استفاده شده است.

مثال

پاسخ معادله لاپلاس زیر را با توجه به شرایط مرزی ارائه شده، بیابید. این معادله توزیع دما در یک صفحه مستطیلی را نشان می‌دهد.

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

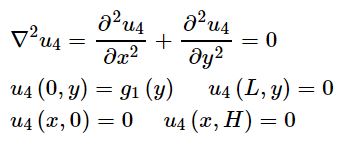
در ابتدا با استفاده از روش جداسازی متغیر‌ها، پاسخ معادله فوق را به‌صورت زیر در نظر می‌گیریم.

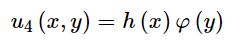
با جایگذاری پاسخ بالا در رابطه ۱ داریم:

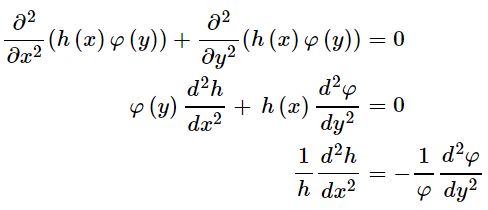
توجه داشته باشید که سمت چپ رابطه بالا از جنس x و سمت راست از جنس y است؛ بنابراین سمت چپ و راست رابطه فوق تنها زمانی با هم برابر هستند که هر دو برابر با عدد ثابت λ باشند؛ از این رو رابطه بالا را برابر با λ قرار داده و به شکل زیر بازنویسی می‌کنیم.

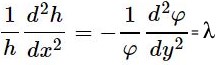
عبارت بالا را می‌توان در قالب دو معادله دیفرانسیل ساده و به شکل زیر بازنویسی کرد:

هم‌چنین با جایگذاری توابع $$\varphi$$ و h در شرایط مرزی، داریم:

در مطلب جداسازی متغیر‌ها، نحوه بدست آوردن λ_n و توابع (φ_n(y را بیان کردیم. این مقادیر برابر بودند با:

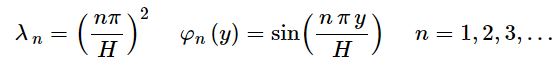
توجه داشته باشید که در مثالِ مطلبِ جداسازی متغیر‌ها، مشتق زمانی از مرتبه اول و مشتق مکانی از مرتبه دوم بود؛ این در حالی است که در معادله لاپلاس، مشتقات نسبت به تمامی متغیر‌ها از مرتبه دوم هستند. با جایگذای مقدار $$\sqrt{\lambda}$$ در رابطه مربوط به h، داریم:

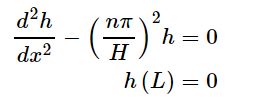
با توجه به مثبت بودن ریشه معادله مشخصه مربوط به h ($$r=\pm(n \pi /H)$$) تابع h برابر است با:

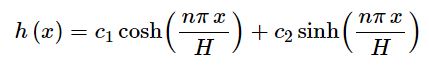
رابطه بالا شرط h(L)=0 را ارضا نمی‌کند؛ جهت حل این مشکل، ضرایب ثابتِ c را می‌توان به نحوی در نظر گرفت که پاسخ به‌شکل زیر باشد.

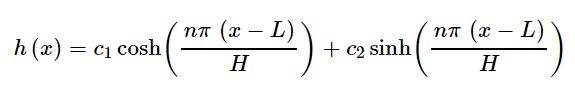
با اعمال شرط مرزی h(L)=0، مقدار c₁ برابر با صفر بدست می‌آید. در نتیجه پاسخ h برابر است با:

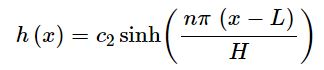
با بدست آمدن توابع (φ(y و (h(x، تابع u برابر خواهد بود با:

جهت بدست آوردن ضرایب ثابت، همانند روش جداسازی متغیر‌ها، می‌توان از سری فوریه استفاده کرد. در حقیقت با اعمال شرایط مرزی در x=0، داریم:

در حقیقت در این مسئله ضریب ثابت برابر با کلِ تابعِ زیر است:

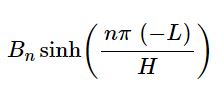
با توجه به رابطه ۳ و استفاده از مفاهیم سری فوریه، تابع بالا برابر است با:

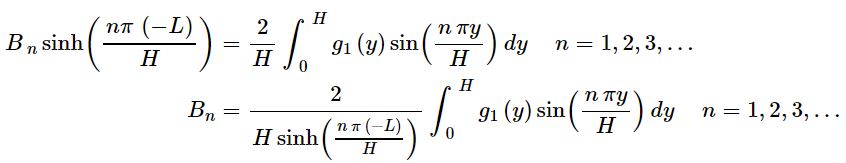
با بدست آمدن ضرایب B_n، مسئله حل شده. در حقیقت باجایگذاری B_n در رابطه ۲، (u(x,y برابر با تابع زیر بدست می‌آید. بنابراین نهایتا تابع (u(x,y برابر است با:

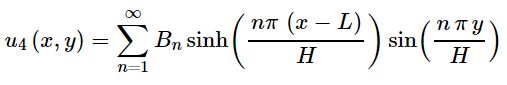
B_n نیز همان رابطه ۴ است. توجه داشته باشید که معادله لاپلاس را می‌توان در دیگر دستگاه‌های مختصات نیز بیان کرد. برای نمونه این معادله در دستگاه مختصات استوانه‌ای به‌صورت زیر است.

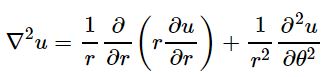
بدیهی است که رابطه بالا نسبت به معادله‌ی دستگاه مختصات کارتزینی پیچیده‌تر است. در مطلبی جداگانه به حل معادلات دیفرانسیل با مشتقات جزئی در دستگاه استوانه‌ای خواهیم پرداخت.

فیلم آموزش ریاضیات مهندسی پیشرفته در فرادرس

کلیک کنید