تابع خودهمبستگی (Autocorrelation Function) – مفاهیم و کاربردها
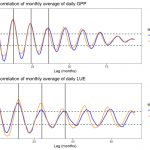
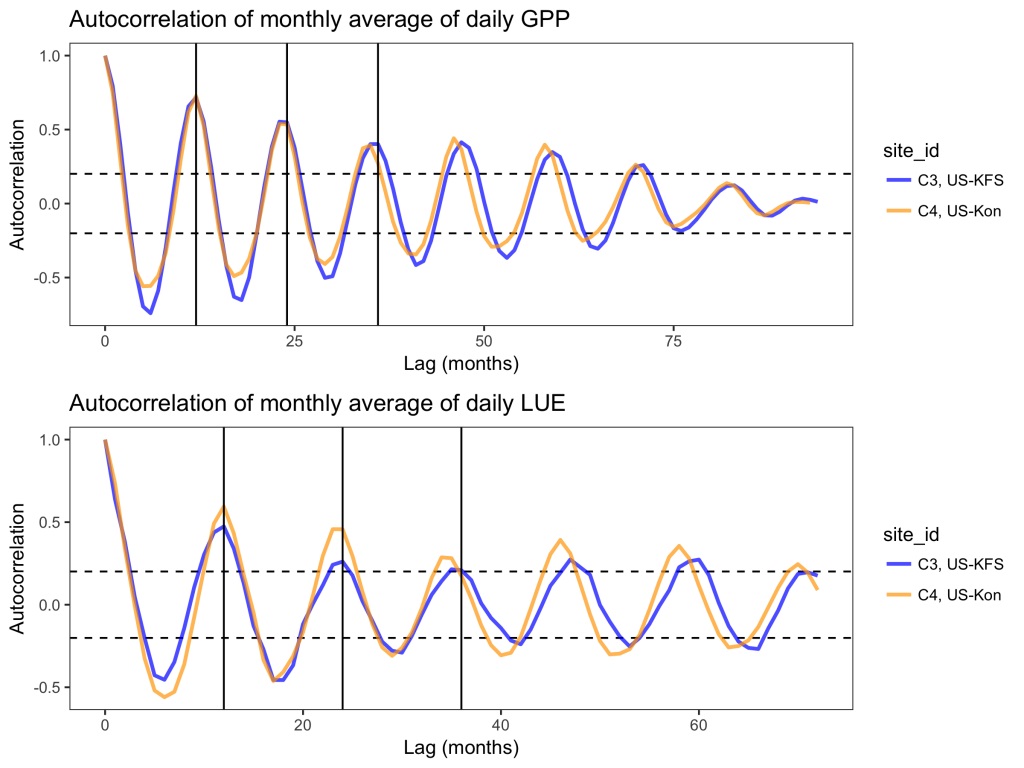
در بحث مربوط به سری زمانی، بین مشاهدات براساس زمان وابستگی وجود دارد. از آنجایی که در آمار، وابستگی را اغلب به صورت همبستگی (Correlation) بیان میکنند، واژه «خود همبستگی» (Autocorrelation) به معنی «همبستگی سریالی» (Serial Correlation) یا وابستگی بین مقدار دنبالهای برحسب زمان است. تابعی که خودهمبستگی را برحسب یک فاصله زمانی بین مشاهدات محاسبه میکند «تابع خودهمبستگی» (Autocorrelation Function) نامیده میشود. در بحث «فرآیندهای تصادفی» (Random Process)، «سری زمانی» (Time Series) و ... از «تابع خودهمبستگی» استفاده میکنند تا به رفتار فرآیند برحسب زمان یا مکان پیببرند. در این نوشتار به بررسی «تابع خودهمبستگی» (Autocorrelation Function) میپردازیم و شیوه استفاده از آن را در تحلیل مدلهای سری زمانی فرا میگیریم.
به منظور آشنایی بیشتر با سریهای زمانی و انواع مدلهای آن به مطلب تحلیل سری زمانی — تعریف و مفاهیم اولیه مراجعه کنید. همچنین به منظور آگاهی از نحوه محاسبه ضریب همبستگی و کوواریانس به مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده مراجعه نمایید.
تابع خودهمبستگی (Autocorrelation Function)
از تابع خودهمبستگی به منظور شناسایی ساختار دادههای مربوط به «سری زمانی» (Time Series) استفاده میشود. اگر دنباله یا سری زمانی را با نشان دهیم، مقدارهای با تاخیر را به صورت خواهیم داشت.
در اینجا منظور از «تاخیر» (Lag) فاصله زمانی است که بین مشاهدات در نظر گرفتهایم. برای مثال اگر میزان تاخیر را ۱ در نظر بگیریم (h=1) آنگاه مشاهدات با تاخیر یک واحد زمانی به صورت زیر نوشته میشوند.
به همین ترتیب اگر (h=2) باشد، مشاهدات برحسب زمانی t به صورت زیر جمعآوری یا نمایش داده میشوند.
به این ترتیب تابع خودهمبستگی یا ACF که مختصر Autocorrelation Function است، همبستگی بین مقدارهای سری زمانی را برحسب تاخیر دلخواه، محاسبه میکند. این تابع به تشخیص پارامتر مدل سری زمانی اتورگرسیو AR یا Autoregresive کمک میکند. همانطور که میدانید مدل اتورگرسیو برای یک سری زمانی ایستا به صورت زیر نوشته میشود.
مشخص است که ارتباط بین مقدار سری در زمان t دارای رابطه خطی با مقدارهای قبلی سری زمانی است. به این ترتیب میتوان گفت که یک رابطه خطی بین مقدار متغیر تصادفی در حال حاضر با مقدارهای گذشته آن وجود دارد.
از آنجا که مدل اتورگرسیو برای سریهای زمانی ایستا قابل استفاده است، شرایط «سری ایستا» (Stationary Series) را مرور میکنیم.
سری زمانی ایستا (Stationary Time Series)
سری زمانی را «ایستا» (Stationary) یا «ایستای ضعیف» (Weak Stationary) مینامند اگر شرایط زیر برایش برقرار باشد.
- امید ریاضی سری زمانی برحسب زمان تغییر نکند، یعنی .
- واریانس سری زمانی برحسب زمان تغییر نکند، یعنی .
- کوواریانس (همبستگی) بین و به زمان بستگی نداشته باشد.
زمانی که سری زمانی ایستا باشد، قادر هستیم براساس مدلهای مرتبط با سری زمانی، رفتار فرآیند را برحسب زمان توضیح دهیم. در غیر اینصورت تا زمانی که سری زمانی ایستا نشود، امکان استفاده از مدلهای سری زمانی معمول وجود ندارد. حال با توجه مفهوم ایستایی سری زمانی، به معرفی تابع خودهمبستگی میپردازیم. از آنجایی که در محاسبه تابع خودهمبستگی از کوواریانس و همچنین واریانس سری زمانی استفاده میشود، اگر سری ایستا نباشد، امکان محاسبه تابع خودهمبستگی وجود نخواهد داشت.
تعریف تابع خودهمبستگی
فرض کنید یا مقدار سری زمانی را در زمان نشان دهد. تابع خودهمبستگی برای این سری زمانی، ضرایب همبستگی بین مشاهدات و را براساس نشان میدهد. بنابراین از لحاظ محاسباتی خودهمبستگی بین و به صورت زیر قابل محاسبه است.
از آنجایی که در سری ایستا، واریانس به بستگی ندارد میتوان با جایگزینی مخرج کسر، عبارت بالا را به صورت سادهتری نیز نوشت.
به این ترتیب مخرج کسر ثابت بوده و از طرف دیگر میدانیم یکی از شرایط سری ایستا، ثابت بودن کوواریانس نیز هست. در این صورت انتظار داریم در یک سری زمانی ایستا، مقدار تابع خود همبستگی براساس تاخیر h تابعی از h باشد. این موضوع اساس تشکیل تابع خود همبستگی را نشان میدهد. بسیاری از سریهای زمانی ایستا، دارای الگوی مشخصی برای تابع خود همبستگی هستند.
سری زمانی اتورگرسیو مرتبه ۱ و الگوی ACF
همانطور که میدانید مدل مربوط به اتورگرسیو مرتبه اول به صورت زیر نوشته میشود.
در اینجا فرض براین است که نوفهها (Noise)، مستقل و دارای توزیع نرمال با میانگین صفر و واریانس ثابت هستند. خصوصیات مربوط به نوفهها نیز نسبت به Xها مستقل است. به علاوه سری زمانی در اینجا ایستا در نظر گرفته شده است. البته باید توجه داشت که شرط ایستایی در اینجا به صورت در خواهد آمد.
خصوصیات مدل اتورگرسیو مرتبه ۱
برای محاسبه میانگین و واریانس و تابع خودهمبستگی در مدل اتورگسیو مرتبه ۱ از رابطههای زیر استفاده میکنیم.
- محاسبه میانگین سری زمانی
- محاسبه واریانس سری زمانی
- محاسبه ضریب همبستگی بین مشاهدات با فاصله h
مثال ۱
فرض کنید دادههای یک سری زمانی مطابق جدول زیر ارائه شده است.
| زمان | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| مقدار | 1 | 10 | 30 | 20 | 15 | 18 | 30 | 80 | 60 |
| زمان | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| مقدار | 70 | 80 | 10 | 30 | 15 | 20 | 35 | 88 | 65 |
| زمان | 19 | 20 | |||||||
| مقدار | 70 | 80 |
مقدارهای تابع خودهمبستگی و همینطور نمودار مربوط به آن برحسب تاخیر (Lag) های مختلف در ادامه قابل مشاهده است. این مقدارها و نمودار توسط دستورات زیر در نرمافزار R محاسبه و نمایش داده شدهاند.
1x=c(1,10,30,20,15,18,30,80,
2 60,70,80,10,30,15,20,35,88,65,70,80)
3acfx=acf(x)
4acfx$acfهمانطور که مشخص است تابع acf وظیفه محاسبه خودهمبستگی را دارد. خروجی به صورت زیر خواهد بود.
1, , 1
2
3 [,1]
4 [1,] 1.00000000
5 [2,] 0.49544581
6 [3,] 0.24521653
7 [4,] 0.03793315
8 [5,] -0.33064697
9 [6,] -0.36949100
10 [7,] -0.22492915
11 [8,] -0.12034540
12 [9,] 0.05813763
13[10,] 0.25223735
14[11,] 0.17743140
15[12,] 0.18749063
16[13,] 0.06527465
17[14,] -0.05737686نمودار تابع خودهمبستگی نیز در تصویر زیر قابل مشاهده است. مشخص است که نمودار به صورت نزولی برحسب تاخیر است. یعنی هرچه مشاهدات با تاخیر بیشتری باشند، همبستگی کمتری پیدا میکنند. ولی بعد از تاخیر ۴ به نظر میرسد که همبستگی شدید ولی به صورت معکوس است. ولی به مرور دوباره کاهش یافته و در انتها نیز ضریب همبستگی برای تاخیری برابر با ۱۳، بسیار کوچک (0.05737686-) شده است.
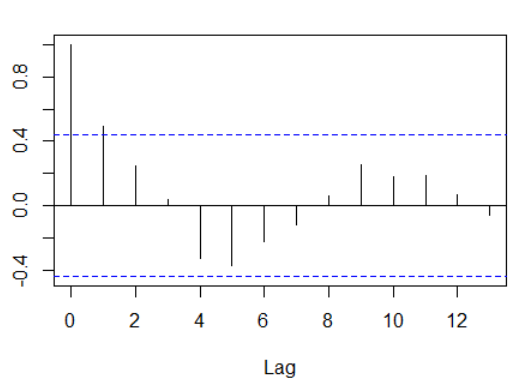
همانطور که دیده میشود ضریب خودهمبستگی برای تاخیر ۰ (که به معنی همبستگی سری با خودش است) برابر با 1 محاسبه شده. به ترتیب با افزایش تاخیرها نیز مقدار همبستگی کاهش یافته و دوباره افزایشی میشود ولی در انتها به صفر نزدیک میشود.
مثال ۲
در این مثال با فرض وجود یک سری زمانی از مدل اتورگرسیو مرتبه اول با ضریب همبستگی 0.6 نمودار زیر را ایجاد کردهایم. به کاهش ضریب همبستگی با افزایش تاخیرات توجه کنید. به نظر میرسد که میزان کاهش به صورت نمایی است.
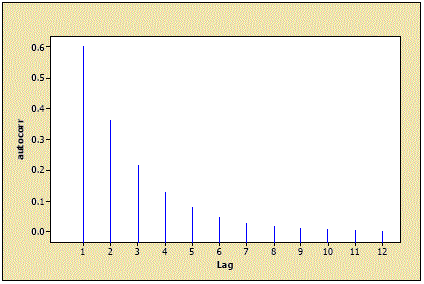
حال فرض کنید که شیب خط مدل اتورگرسیو مرتبه ۱، منفی مثلا برابر با 0.7- باشد. ممکن است شکل نمودار تابع خودهمبستگی آن به صورت زیر دربیاید. توجه دارید که شرط ایستا بودن در مدل اتورگرسیو است که در این جا محقق شده است.
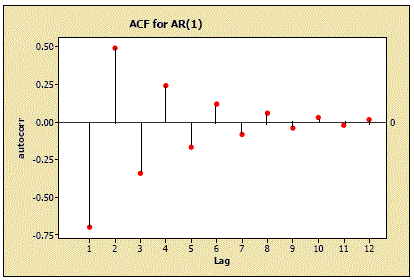
در این حالت الگو به صورت نزولی ولی تناوبی است. به این معنی که قدرمطلق تابع خودهمبستگی نزولی برحسب تاخیرات است. این الگوی نزولی برای و نزولی تناوبی برای مربوط به مدل اتورگرسیو مرتبه ۱ بود. بنابراین اگر برای دادههایی الگوری ACF به این صورت باشد، میتوان مدل اتورگرسیو مرتبه ۱ را به آن اختصاص داد. مشخص است روند کاهش برای هر دو حالت به صورت نمایی است و در انتها به صفر نزدیک میشود.
ارتباط بین ACF و سریهای زمانی ناایستا
تابع خودهمبستگی را میتوان برای سریهای زمانی ناایستا نیز ترسیم و محاسبه کرد.
فرض کنید که با یک سری زمانی به همراه الگوی روند روبرو هستیم. در زیر چنین سری زمانی ترسیم شده است.

از آنجایی که بطور متوسط الگوی روند چنین دادههایی صعودی است نمودار تابع خودهمبستگی به صورت زیر درخواهد آمد.
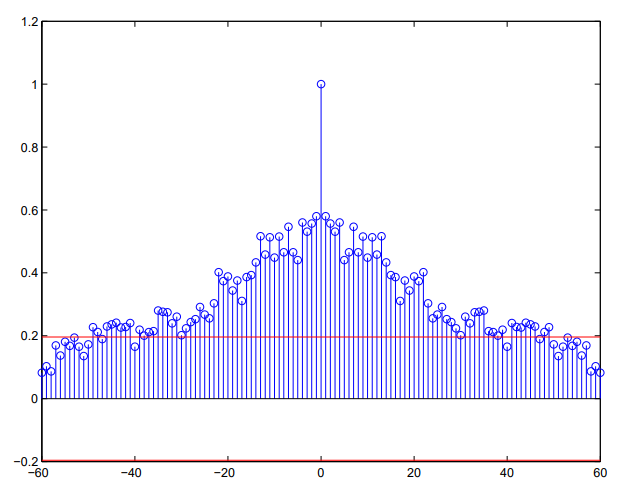
مشخص است که در این نمودار به ازای های منفی و مثبت نمودار ترسیم شده است. تقارن نسبت به نقطه ۰ در نمودار دیده میشود. در ضمن هر چه تاخیر یا افزایش مییابد، میزان همبستگی کمتر میشود ولی سرعت کاهش این مقدار به آهستگی صورت میگیرد. به نظر میرسد همبستگی مقدارها در زمان اولیه و در انتهای سری، به صفر نزدیک شده است.
حال به بررسی الگوی تابع خودهمبستگی برای سری زمانی با «الگوی فصلی» (Seasonal) یا «تناوبی» (Periodic) میپردازیم. فرض کنید دادههای سری زمانی مطابق با تصویر زیر در اختیارمان باشد.
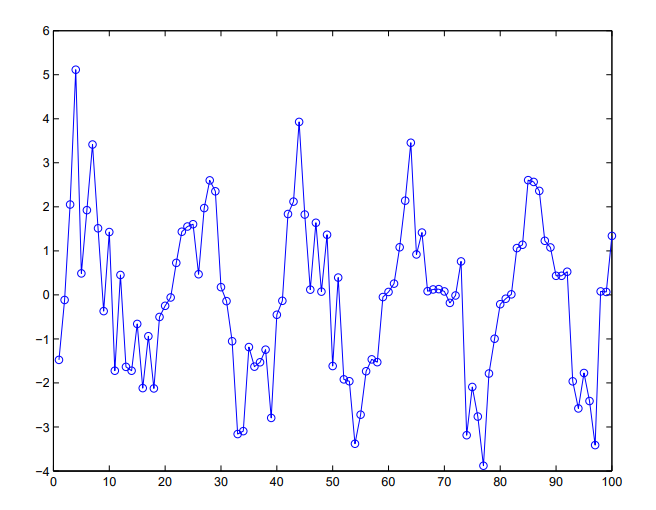
اگر برای چنین دادههایی، نمودار مربوط به تابع خودهمبستگی را ترسیم کنیم به شکلی مانند زیر خواهیم رسید.
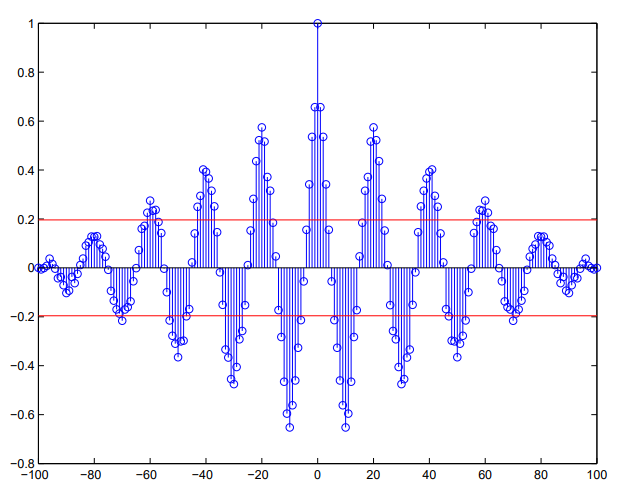
همانطور که دیده میشود، باز هم این نمودار به صورت نزولی ولی به همراه تناوب است. در زمان یا تاخیری که دادههای متناوب ظاهر میشوند، ضریب همبستگی افزایش یافته و به حداکثر رسیده و سپس به مرور کاهش مییابد. چنین الگویی در نمودار تابع خودهمبستگی نشاندهنده وجود تناوب در سری زمانی است.
اینبار به یک سری زمانی ایستا با مدل میانگین متحرک مرتبه ۱ میپردازیم. با استفاده از کد دستوری R که در زیر قابل مشاهده است، شبیه سازی چنین دادههای را انجام دادهایم.
1# An ARIMA simulation
2ts.sim <- arima.sim(list(order = c(0,1,0)), n = 20)
3ts.plot(ts.sim)نمودار چنین دادههای به صورت زیر ظاهر خواهد شد. مشخص است که این سری زمانی ایستا است.
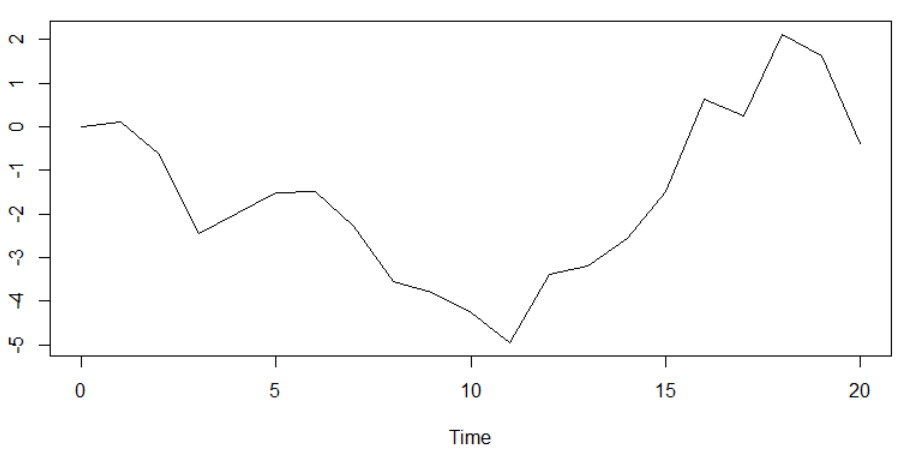
نمودار مربوط به تابع خودهمبستگی برای چنین دادههایی به صورت زیر در خواهد آمد.

شکل این نمودار، در ابتدا نزولی ولی بعد به صورت صعودی درآمده است. ولی تقریبا میزان کاهش یا افزایش ضریب خودهمبستگی به صورت خطی تغییر مییابد.
حال به بررسی مدل (AR(1 میپردازیم. با استفاده از کد زیر دادههای مربوط به چنین مدلی را شبیه سازی کردهایم.
1# An ARIMA simulation
2ts.sim.ar1 <- arima.sim(list(ar=.9), n = 20)
3ts.plot(ts.sim.ar1)
4acf(ts.sim.ar1)نکته: در کد بالا منظور از ar=0.9، تعیین شیب خط مدل اتورگرسیو است.
نمودار چنین دادههایی به صورت زیر خواهد بود. باز هم مشخص است که این سری، ایستا است.
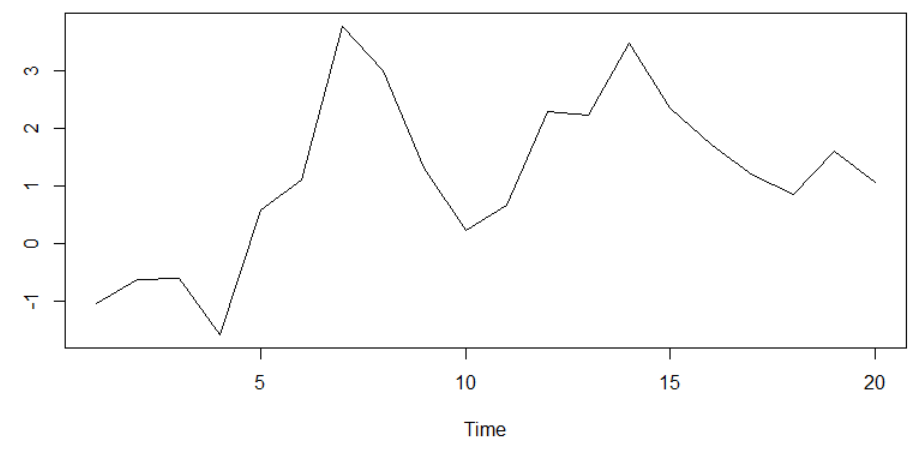
به این ترتیب با رسم تابع خودهمبستگی، به تصویری مانند شکل زیر خواهیم رسید. مشخص است که سرعت کاهش مقدار ضریب خودهمبستگی در این حالت شدیدتر از حالتهای دیگر است و زودتر به صفر نزدیک میشود. روند تغییرات ضریب خودهمبستگی در اینجا به صورت نمایی است.
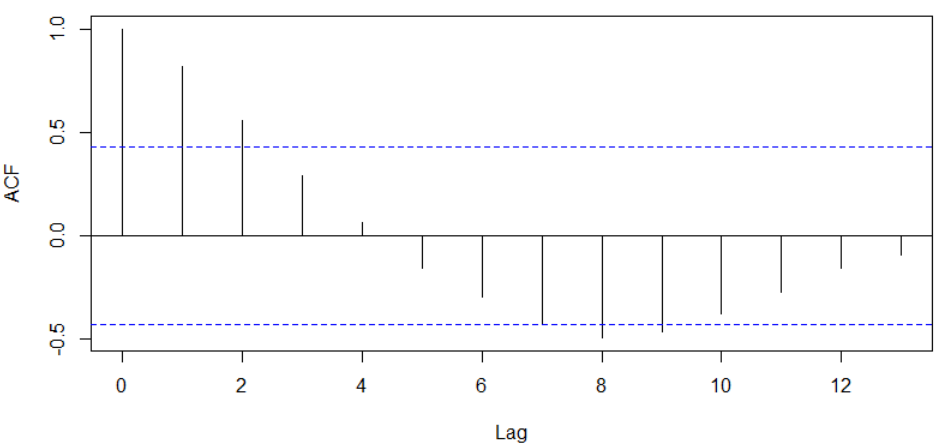
حال به نمودار خودهمبستگی نوفه (Noise) با توزیع نرمال نگاهی بیاندازیم. اگر نمونهای 20 تای از توزیع نرمال را به عنوان سری زمانی در نظر بگیریم، ایستایی سری زمانی که مشخص است. حال کافی است که مقدار تابع خودهمبستگی و نمودار آن را رسم کنیم.
1# An ARIMA simulation
2noise.ts.sim.ar1 <- arima.sim(list(order(0,0,0)),n = 20)
3ts.plot(noise.ts.sim.ar1)
4acf(noise.ts.sim.ar1)با توجه به اینکه پارامترهای مدل سری زمانی را همگی صفر انتخاب کردهایم، دادههای تولیدی نوفه هستند. بنابراین الگو یا همبستگی درونی بین آنها وجود ندارد. بنابراین نمودار این سری زمانی الگو یا روندی را نشان نمیدهد و ایستا است. شکل نمودار این سری به صورت زیر است.
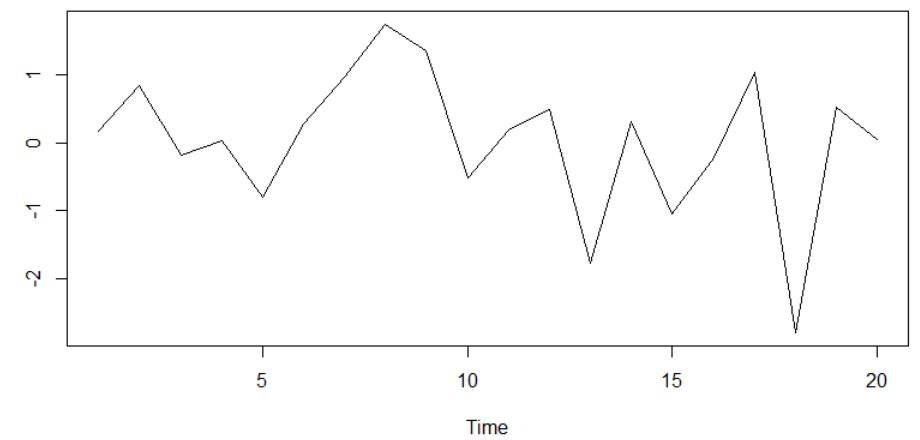
برهمین اساس، نمودار خودهمبستگی به صورت زیر است. مقدار ضرایب همبستگی برحسب تاخیرها (Lag) نیز محاسبه شدهاند.
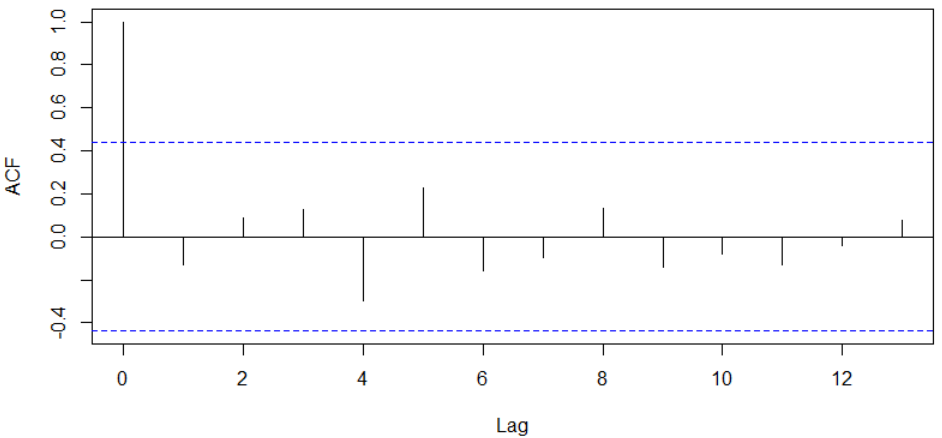
مشخص است که این نمودار، نه دارای روند کاهشی خطی مانند مدل MA است و نه دارای مدل روند کاهش نمایی مانند AR است. حتی الگوی تناوبی را نیز نمایش نمیدهد. البته انتظارمان از سری زمانی براساس نوفه نیز همین بود زیرا باید نمونههای مستقل، هم توزیع و با واریانس و میانگین ثابت باشند. وجود استقلال باعث عدم وابستگی به زمان در این سری زمانی است. بنابراین تعیین الگوی یا مدل سری زمانی برای آن کار درستی نیست.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزشهای پیشبینی و تحلیل سریهای زمانی
- آموزش تحلیل و پیشبینی سری های زمانی
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های کاربردی شبکه های عصبی مصنوعی
- مجموعه آموزش های مباحث تئوری و عملی موجک ها در متلب
- آموزش متلب با نگرش تحلیل آماری، تحلیل سری های زمانی و داده های مکانی
^^













سلام ووقت به خیر
توضیحی داده نشده که چگونه یک سری زمانی که خود همبستگی دارد را حل این مشکل کنیم.
بسیار عالی بود. سپاس از استاد ری بد و مجله بی نظیر فرادرس.
ممنون از توضیحات مفیدتون