پیشتر در وبلاگ فرادرس مفاهیم پایهای انتگرال ، انتگرال دوگانه و انتگرال سهگانه را نیز توضیح دادیم. انتگرالهای دوگانه و سهگانه نوعی انتگرال مکرر محسوب میشوند. در این مطلب مفهوم انتگرال مکرر را با جزئیاتی بیشتر توضیح خواهیم داد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
انتگرال مکرر
انتگرال مکرر، به عبارتی گفته میشود که در آن از یک تابع چندمتغیره به صورت پیدرپی انتگرال گرفته شده است. بنابراین انتگرال دوگانه یا سهگانه به نحوی انتگرال مکرر محسوب میشوند.
قویترین ابزار به منظور محاسبه انتگرال دوگانه، «قضیه فوبینی» (Fubini’s theorem) است. این ابزار تنها برای ناحیههایی که اصطلاحا آنها را نوع اول و نوع دوم مینامند، کاربرد دارد.
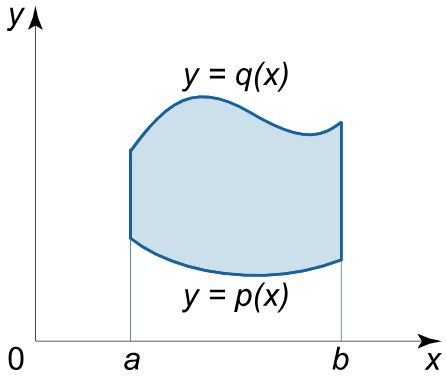
ناحیه نوع اول
ناحیهای تحت عنوان R R R x x x
R = { ( x , y ) ∣ a ≤ x ≤ b , p ( x ) ≤ y ≤ q ( x ) } \large { R } = { \left\{ {\left( { x , y } \right)| \;a \le x \le b,\;\;}\right.} \kern0pt {\left.{ p \left ( x \right ) \le y \le q\left( x \right)} \right\} \;\;} R = { ( x , y ) ∣ a ≤ x ≤ b , p ( x ) ≤ y ≤ q ( x ) }
ناحیه انتگرالگیری نوع اول ناحیه نوع دوم
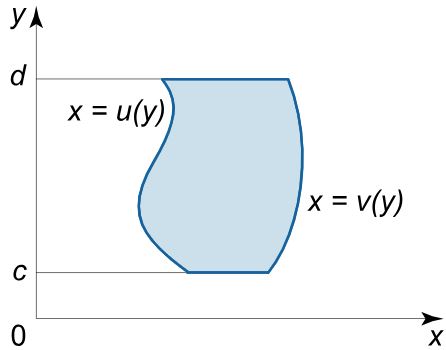
ناحیه R R R y y y
ناحیه انتگرالگیری نوع دوم قضیه فوبینی
فرض کنید f ( x , y ) f ( x , y ) f ( x , y ) R R R
R = { ( x , y ) ∣ a ≤ x ≤ b , p ( x ) ≤ y ≤ q ( x ) } \large {R } = { \left \{ {\left ( { x , y } \right)|\;a \le x \le b,\;\;}\right.}\kern0pt { \left.{p\left ( x \right ) \le y \le q\left( x \right)} \right \} } R = { ( x , y ) ∣ a ≤ x ≤ b , p ( x ) ≤ y ≤ q ( x ) }
در این صورت انتگرال دوگانه تابع f ( x , y ) f(x,y) f ( x , y )
∬ R f ( x , y ) d A = ∫ a b ∫ p ( x ) q ( x ) f ( x , y ) d y d x \large { \iint \limits _ R { f \left ( { x , y } \right ) d A} } = { \int \limits _ a ^ b { \int \limits _ { p \left ( x \right ) } ^ { q \left( x \right ) } { f \left( { x , y } \right ) d y d x } } } R ∬ f ( x , y ) d A = a ∫ b p ( x ) ∫ q ( x ) f ( x , y ) d y d x
دقیقا برای ناحیهای از نوع دوم نیز میتوان گزارهای مشابه را بیان کرد. در این حالت نیز f ( x , y ) f \left ( { x , y } \right) f ( x , y ) R R R
R = { ( x , y ) ∣ u ( y ) ≤ x ≤ v ( y ) , c ≤ y ≤ d } \large { R } = { \left\{ {\left ( { x , y } \right ) |\;u \left ( y \right) \le x \le v\left( y \right ),\;\;}\right.} \kern0pt {\left.{c \le y \le d} \right\} } R = { ( x , y ) ∣ u ( y ) ≤ x ≤ v ( y ) , c ≤ y ≤ d }
در این صورت انتگرال مکرر به صورت زیر محاسبه میشود.
∬ R f ( x , y ) d A = ∫ c d ∫ u ( y ) v ( y ) f ( x , y ) d x d y \large {\iint \limits_R {f\left( { x , y } \right)dA} } = { \int \limits _ c ^ d {\int \limits _ { u \left ( y \right ) } ^ { v \left ( y \right ) } { f \left ( { x , y } \right) d xd y }}} R ∬ f ( x , y ) d A = c ∫ d u ( y ) ∫ v ( y ) f ( x , y ) d x d y
سخن را کوتاه کرده و به ذکر مثالهایی میپردازیم.
مثال ۱
حاصل انتگرال مکرر زیر را بدست آورید.
∫ 0 1 ∫ 1 2 x y d y d x \large \begin {align*} \int \limits _ 0 ^ 1 { \int \limits _ 1 ^ 2 { x y d yd x } } \end {align*} 0 ∫ 1 1 ∫ 2 x y d y d x
همانطور که بیان شد باید در ابتدا انتگرال داخلی محاسبه شده، سپس انتگرال بیرونی را بدست میآوریم.
∫ 0 1 ∫ 1 2 x y d y d x = ∫ 0 1 [ ∫ 1 2 x y d y ] d x = ∫ 0 1 [ x ( y 2 2 ) ∣ 1 2 ] d x = ∫ 0 1 3 2 d x = 3 2 ( x 2 2 ) ∣ 0 1 = 3 4 \large \begin {align*} { \int \limits _ 0 ^ 1 { \int \limits _ 1 ^ 2 { x y d y d x } } } & = { \int \limits_0^1 {\left[ {\int\limits_1^2 { x y d y } } \right] d x } } \\ & = {\int\limits_0^1 {\left[ {x\left. {\left( {\frac { { {y ^ 2 } }} { 2 } } \right ) } \right|_1^2} \right] d x } } \\ & = {\int\limits_0^1 {\frac{3}{2}dx} } = {\frac{3}{2}\left. {\left ( { \frac { { {x ^ 2 } }} { 2 } } \right)} \right|_0^1 } \\ & = { \frac { 3} { 4 } } \end {align*} 0 ∫ 1 1 ∫ 2 x y d y d x = 0 ∫ 1 1 ∫ 2 x y d y d x = 0 ∫ 1 x ( 2 y 2 ) 1 2 d x = 0 ∫ 1 2 3 d x = 2 3 ( 2 x 2 ) 0 1 = 4 3
مثال ۲
حاصل انتگرال مکرر زیر را بیابید.
∫ 0 1 ∫ y y 2 ( x + 2 y ) d x d y \large \begin {align*} \int \limits _ 0 ^ 1 { \int \limits _ y ^ { { y^ 2 } } { \left ( { x + 2 y } \right ) d x d y } } \end {align*} 0 ∫ 1 y ∫ y 2 ( x + 2 y ) d x d y
همانطور که میبینید بازههای انتگرال بر حسب y y y
∫ 0 1 ∫ y y 2 ( x + 2 y ) d x d y = ∫ 0 1 [ ∫ y y 2 ( x + 2 y ) d x ] d y = ∫ 0 1 [ ( x 2 2 + 2 y x ) ∣ y y 2 ] d y = ∫ 0 1 [ ( y 4 2 + 2 y 3 ) − ( y 2 2 + 2 y 2 ) ] d y = ∫ 0 1 [ y 4 2 + 2 y 3 – 5 y 2 2 ] d y = [ y 5 10 + y 4 2 – 5 y 3 6 ] ∣ 0 1 = 1 10 + 1 2 – 5 6 = – 7 30 \large \begin {align*} { \int \limits _ 0 ^ 1 { \int \limits _ y ^ { { y ^ 2 } } { \left ( { x + 2 y } \right ) d x d y } } } & = { \int \limits _ 0 ^ 1 { \left [ { \int \limits _ y ^ { {y ^ 2 } } {\left( { x + 2 y } \right) d x } } \right] d y } } \\ & = { \int \limits _ 0 ^ 1 {\left[ {\left. {\left( {\frac { { { x ^ 2 } } } {2} + 2 y x } \right ) } \right|_ y ^ { { y ^2 } } } \right] d y } } \\ & = {\int \limits _ 0 ^ 1 {\left[ {\left( {\frac { { { y ^ 4} } }{ 2} + 2 { y ^ 3 } } \right ) } \right.} - { \left.{ \left ( {\frac { {{ y ^ 2 } }} { 2 } + 2 { y ^2 } } \right ) } \right] d y } } \\ & = { \int \limits _ 0 ^ 1 { \left[ {\frac{ { { y ^ 4} } } { 2} + 2 { y ^ 3} – \frac { { 5{ y ^ 2 }} }{ 2 }} \right] d y } } \\ & = {\left. {\left[ {\frac { { { y ^ 5 } } } {{ 1 0 }} + \frac { { {y ^ 4 } } } {2} – \frac { { 5 {y ^ 3} }} {6}} \right]} \right|_0^1 } = {\frac { 1} { { 10 } } + \frac { 1}{ 2 } – \frac { 5 } { 6 } } \\ & ={ – \frac { 7 } { { 30 } }} \end {align*} 0 ∫ 1 y ∫ y 2 ( x + 2 y ) d x d y = 0 ∫ 1 y ∫ y 2 ( x + 2 y ) d x d y = 0 ∫ 1 ( 2 x 2 + 2 y x ) y y 2 d y = 0 ∫ 1 [ ( 2 y 4 + 2 y 3 ) − ( 2 y 2 + 2 y 2 ) ] d y = 0 ∫ 1 [ 2 y 4 + 2 y 3 – 2 5 y 2 ] d y = [ 10 y 5 + 2 y 4 – 6 5 y 3 ] 0 1 = 10 1 + 2 1 – 6 5 = – 30 7
مثال ۳
حاصل انتگرال مکرر زیر را بیابید.
∫ 1 2 ∫ 0 y x ( y 2 + x 2 ) d x d y \large \int \limits _ 1 ^ 2 { \int \limits _ 0 ^ y { x \sqrt { \left( {{y ^ 2 } + { x ^ 2 } } \right) } d x d y }} 1 ∫ 2 0 ∫ y x ( y 2 + x 2 ) d x d y
مشابه با مثال ۲ در این حالت نیز از قضیه فوبینی به صورت زیر استفاده میکنیم.
∫ 1 2 ∫ 0 y x y 2 + x 2 d x d y \large \int \limits _ 1 ^ 2 { \int \limits _ 0 ^ y { x \sqrt { { y ^ 2 } + { x ^ 2 } } d x d y } } 1 ∫ 2 0 ∫ y x y 2 + x 2 d x d y
این مسئله از این جهت متفاوت است که حاصل انتگرال درونی را باید با استفاده از تغییر متغیر زیر بدست آورد.
z = y 2 + x 2 ⇒ d z = 2 x d x ⇒ x d x = d z 2 \large {z = { y ^ 2 } + { x ^ 2 } \;\;} \Rightarrow { d z = 2 x d x \;\;}\Rightarrow { x d x = \frac { { d z } } { 2 } } z = y 2 + x 2 ⇒ d z = 2 x d x ⇒ x d x = 2 d z
بدیهی است که بازهها نیز باید در متغیر جدید بیان شوند. زمانی که x = 0 x = 0 x = 0 z = y 2 z = y ^ 2 z = y 2 x = y x = y x = y z = 2 y 2 z =2y^2 z = 2 y 2
I = ∫ 1 2 [ ∫ 0 y x y 2 + x 2 d x ] d y = ∫ 1 2 [ ∫ y 2 2 y 2 z d z 2 ] d y = ∫ 1 2 [ ( z 3 2 3 ) ∣ y 2 2 y 2 ] d y = 1 3 ∫ 1 2 [ ( 2 y 2 ) 3 2 – ( y 2 ) 3 2 ] d y = 1 3 ∫ 1 2 [ 2 2 y 3 – y 3 ] d y = 2 2 – 1 3 ∫ 1 2 y 3 d y = 2 2 – 1 12 ( y 4 ) ∣ 1 2 = 5 ( 2 2 – 1 ) 4 \large \begin{align*} {I } & = { \int \limits _ 1 ^ 2 { \left[ { \int \limits _ 0 ^ y { x \sqrt { { y ^ 2 } + { x ^ 2 } } d x } } \right] d y } } \\ & = {\int\limits_1^2 {\left[ {\int\limits_ { {y ^ 2 } } ^ { 2 { y ^ 2 } } { \sqrt z \frac { { d z } } { 2}} } \right]dy} } \\ & = {\int\limits_1^2 {\left[ {\left. { \left ( { \frac { { { z ^ { \frac { 3 } {2 } }} } }{3}} \right)} \right|_{ { y ^ 2 }} ^ {2 { y ^ 2 } } } \right] d y } } \\ & = {\frac { 1 } {3 }\int\limits_1^2 {\left[ { { {\left( {2{y^2}} \right)}^{\frac { 3 } { 2} } } – {{\left( {{y^2}} \right)} ^ { \frac { 3 } { 2} } } } \right] d y } } \\ & = { \frac { 1 } {3 } \int \limits_1^2 {\left[ {2\sqrt 2 { y ^ 3 } – { y ^ 3 } } \right]dy} } \\ & = {\frac { { 2 \sqrt 2 – 1} } { 3 } \int\limits_1^2 { { y ^ 3} d y } } = {\frac{{2\sqrt 2 – 1} } { { 1 2 } } \left. {\left ( { { y ^ 4 } } \right)} \right|_1^2 } \\ & = {\frac{{5\left( {2\sqrt 2 – 1} \right ) } }{4} } \end{align*} I = 1 ∫ 2 0 ∫ y x y 2 + x 2 d x d y = 1 ∫ 2 y 2 ∫ 2 y 2 z 2 d z d y = 1 ∫ 2 ( 3 z 2 3 ) y 2 2 y 2 d y = 3 1 1 ∫ 2 [ ( 2 y 2 ) 2 3 – ( y 2 ) 2 3 ] d y = 3 1 1 ∫ 2 [ 2 2 y 3 – y 3 ] d y = 3 2 2 –1 1 ∫ 2 y 3 d y = 12 2 2 –1 ( y 4 ) 1 2 = 4 5 ( 2 2 –1 )
مثال ۴
حاصل انتگرال تکراری ∫ 0 1 ∫ 0 y ln ( y 2 + 1 ) d x d y \int \limits _ 0 ^ 1 { \int \limits _ 0 ^ y { \ln \left ( { { y ^ 2 } + 1 } \right ) d x d y } } 0 ∫ 1 0 ∫ y ln ( y 2 + 1 ) d x d y
در ابتدا باید حاصل انتگرال داخلی به صورت زیر محاسبه شود.
I = ∫ 0 1 ∫ 0 y ln ( y 2 + 1 ) d x d y = ∫ 0 1 [ ∫ 0 y ln ( y 2 + 1 ) d x ] d y = ∫ 0 1 [ ln ( y 2 + 1 ) x ∣ 0 y ] d y = ∫ 0 1 ln ( y 2 + 1 ) y d y \large \begin {align*} { I } & ={ \int \limits_0^1 {\int\limits _ 0 ^ y { \ln \left ( { { y ^ 2 } + 1} \right ) d x d y } } } \\ & = { \int \limits _ 0 ^ 1 { \left [ { \int \limits _ 0 ^ y {\ln \left( {{y^2} + 1} \right ) d x } } \right] d y } } \\ & = {\int\limits_0^1 {\left[ {\ln \left( {{y^2} + 1} \right)\left. x \right| _ 0 ^ y } \right] d y } } \\ & = { \int \limits _ 0 ^ 1 { \ln \left ( { { y ^ 2 } + 1} \right) y d y } } \end {align*} I = 0 ∫ 1 0 ∫ y ln ( y 2 + 1 ) d x d y = 0 ∫ 1 0 ∫ y ln ( y 2 + 1 ) d x d y = 0 ∫ 1 [ ln ( y 2 + 1 ) x ∣ 0 y ] d y = 0 ∫ 1 ln ( y 2 + 1 ) y d y
به منظور محاسبه انتگرال لگاریتمی فوق، میتوان از روش جزء به جزء استفاده کرد. بدین منظور توابع u u u d v dv d v
u = ln ( y 2 + 1 ) , d v = y d y \large u = \ln \left ( { { y ^ 2 } + 1 } \right ) \ \ , \ \ d v = y d y u = ln ( y 2 + 1 ) , d v = y d y
بنابراین دیفرانسیلِ d u d u d u v v v
d u = d d y ln ( y 2 + 1 ) = 2 y d y y 2 + 1 , v = ∫ y d y = y 2 2 \large { d u = \frac { d } { { d y } } \ln \left ( { { y ^ 2 } + 1 } \right ) } = { \frac { { 2 y d y } } { { { y ^ 2 } + 1 } } \;\; ,\;\;}\kern-0.3pt {v = \int { y d y } = \frac { { { y ^ 2 } } }{ 2 } } d u = d y d ln ( y 2 + 1 ) = y 2 + 1 2 y d y , v = ∫ y d y = 2 y 2
لذا حاصل انتگرال به صورت زیر سادهتر خواهد شد.
I = ∫ 0 1 ln ( y 2 + 1 ) y d y = [ y 2 2 ln ( y 2 + 1 ) ] ∣ 0 1 − ∫ 0 1 y 2 2 2 y d y y 2 + 1 = [ y 2 2 ln ( y 2 + 1 ) ] ∣ 0 1 − ∫ 0 1 y 3 d y y 2 + 1 = ln 2 2 − ∫ 0 1 y 3 d y y 2 + 1 \large \begin {align*} I & = \int \limits _ 0 ^ 1 { \ln \left ( { { y ^ 2 } + 1 } \right ) y d y } \\ & = { \left. {\left[ {\frac { { { y ^ 2 } } } { 2 } \ln \left( { { y ^ 2 } + 1} \right)} \right]} \right|_0^1 }-{ \int \limits_0^1 {\frac{{{ y ^ 2 } } } { 2 } \frac { { 2 y d y } } { { { y ^2 } + 1 } } } } \\ & = {\left. {\left[ {\frac { {{ y ^ 2 } } } { 2 }\ln \left( { { y ^ 2 } + 1 } \right)} \right]} \right|_0^1 }-{ \int\limits_0^1 {\frac { { { y ^3 } d y } } { { { y ^ 2 } + 1 } } } } \\ & = { \frac { { \ln 2 } } {2} }-{ \int\limits_0^1 {\frac { { { y ^ 3 }d y } } { { {y ^ 2 } + 1} } }} \end {align*} I = 0 ∫ 1 ln ( y 2 + 1 ) y d y = [ 2 y 2 ln ( y 2 + 1 ) ] 0 1 − 0 ∫ 1 2 y 2 y 2 + 1 2 y d y = [ 2 y 2 ln ( y 2 + 1 ) ] 0 1 − 0 ∫ 1 y 2 + 1 y 3 d y = 2 ln 2 − 0 ∫ 1 y 2 + 1 y 3 d y
نهایتا حاصل انتگرال بیرونی نیز برابر است با:
∫ 0 1 y 3 d y y 2 + 1 = ∫ 0 1 y 3 + y – y y 2 + 1 d y = ∫ 0 1 [ y – y y 2 + 1 ] d y = ∫ 0 1 y d y − 1 2 ∫ 0 1 d ( y 2 + 1 ) y 2 + 1 = [ y 2 2 – 1 2 ln ( y 2 + 1 ) ] ∣ 0 1 = 1 2 – ln 2 2 \large \begin {align*} \int \limits _ 0 ^ 1 { \frac { { {y ^ 3 }d y } } { { { y ^ 2} + 1}}} & = { \int \limits _ 0 ^ 1 { \frac { {{ y ^ 3 } + y – y } } { { { y ^2 } + 1 } }d y } } \\ & = {\int\limits_0^1 {\left[ {y – \frac { y} { { { y ^2} + 1} } } \right] d y } } \\ & = {\int\limits_0^1 { y d y } }-{ \frac { 1 } { 2 } \int\limits_0^1 {\frac { { d \left( {{y^2} + 1} \right ) } } { { { y ^ 2} + 1} } } } \\ & = {\left. {\left[ {\frac { { { y ^ 2 } } } { 2 } – \frac { 1} { 2 }\ln \left( {{y^2} + 1} \right)} \right]} \right|_0^1 } \\ & = { \frac { 1 } {2 } – \frac { { \ln 2 } } {2 } } \end {align*} 0 ∫ 1 y 2 + 1 y 3 d y = 0 ∫ 1 y 2 + 1 y 3 + y – y d y = 0 ∫ 1 [ y – y 2 + 1 y ] d y = 0 ∫ 1 y d y − 2 1 0 ∫ 1 y 2 + 1 d ( y 2 + 1 ) = [ 2 y 2 – 2 1 ln ( y 2 + 1 ) ] 0 1 = 2 1 – 2 ln 2
نهایتا با استفاده از مفهوم انتگرال مکرر حاصل انتگرال دوگانه در این مسئله برابر میشود با:
$$ \large \require{cancel} {I = { \frac { { \ln 2 } } { 2} } - ( \frac { 1 }{ 2 } } - { {\frac { { \ln 2 } }{ 2 } } })= \ln 2 - \frac { 1 } { 2 } $$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش انتگرال مکرر — به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی انتگرال مکرر فیلم آموزشی حل چند مثال از انتگرال مکرر