مقاومت سری در مدار — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، درباره مقاومت‌ها و انواع آن بحث کردیم. در این آموزش قصد داریم مقاومت سری را در مدار الکتریکی بررسی کنیم. به اتصال زنجیروار مقاومت‌ها، اتصال سری گفته می‌شود. در این حالت جریان گذرنده از همه مقاومت‌ها با هم برابر است. مقاومت‌ها می‌توانند به صورت سری، متوالی یا سری-متوالی به یکدیگر متصل شوند. به این ترتیب، شبکه مقاومتی حاصل پیچیده‌تر می‌شود و مقاومت معادل آن با محاسبات ریاضی به دست می‌آید.

مقاومت از عناصر بنیادی علم الکترونیک محسوب می‌شود و می‌توان از آن، برای تبدیل ولتاژ به جریان یا جریان به ولتاژ استفاده کرد. با تنظیم صحیح مقدار مقاومت، می‌توان به جریان یا ولتاژ خاص رسید. این ولتاژ یا جریان را می‌توان به عنوان مرجع ولتاژ در مدارها به کار برد. یک شبکه پیچیده از مقاومت‌های سری را می‌توان با یک مقاومت معادل ($$R_{EQ}$$) یا امپدانس معادل ($$Z_{EQ}$$) جایگزین کرد. همه مقاومت‌ها فارغ از پیچیدگی شبکه مداری آنها، از قوانین بنیادی یعنی قانون اهم و قوانین مداری کیرشهف، تبعیت می‌کنند.

مقاومت سری

اگر مقاومت‌ها به صورت زنجیروار و پی در پی به هم متصل شوند، گویند که این مقاومت‌ها با یکدیگر سری هستند. برای مثال، شبکه مقاومتی سری شکل زیر را در نظر بگیرید:

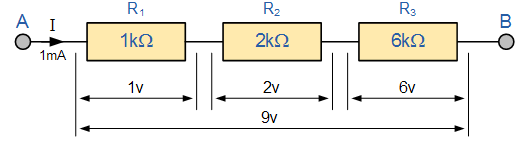
جریان گذرنده از مقاومت اول از مقاومت دوم و سوم نیز می‌گذرد، زیرا مسیر دیگری برای عبور ندارد. بنابراین، از همه مقاومت‌های سری یک جریان مشترک عبور می‌کند و مقدار جریانی که از این شبکه عبور می‌کند، در همه نقاط یکسان است. سه مقاومت $$R_1$$ و $$R_2$$ و $$R_3$$ در این مدار، به صورت سری بین نقاط A و B به یکدیگر متصل شده‌اند و جریان مشترک (I) از آنها عبور می‌کند. فرض کنید این جریان برابر یک میلی‌آمپر باشد. داریم:

$$I_{R1} = I_{R2} =I_{R3} = I_{AB} = 1 mA $$

همانطور که گفتیم، جریان گذرنده از همه مقاومت‌های سری در زنجیره و همچنین مقاومت معادل این مدار ($$R_T$$)، مشابه است. مقاومت معادل یک شبکه سری، برابر با جمع همه مقاومت‌هاست. یعنی:

$$R_T = R_1 + R_2 + R_3$$

با در نظر گرفتن مقادیر مقاومت‌ها در شکل (۱)، مقاومت معادل ($$R_{EQ}$$) به صورت زیر به دست می‌آید:

$$R_{EQ} = R_1 + R_2 + R_3 = 1 k\Omega + 2 k \Omega + 6 k\Omega = 9 k \Omega$$

پس می‌توان این سه مقاومت را با یک مقاومت معادل $$9k\Omega$$ جایگزین کرد. اگر تعداد بیشتری مقاومت با هم سری شوند، مقاومت معادل یا مقاومت کلی مدار ($$R_T$$) با جمع تک تک مقاومت‌ها برابر خواهد بود. با اضافه شدن یک مقاومت به یک شبکه سری صرفنظر از مقدار آن، مقاومت معادل بزرگتر می‌شود. مقاومت کلی یا «مقاومت معادل» (Equivalent Resistance) برای یک مدار در حالت کلی به صورت زیر قابل تعریف است:

تعریف: مقاومت معادل، مقاومتی است که اگر به جای شبکه مقاومتی سری در مدار قرار گیرد، مقادیر جریان یا افت کلی ولتاژ در مدار ثابت بماند.

رابطه لازم برای محاسبه مقاومت کلی مدار در حالت اتصال سری به صورت زیر است:

$$R_{Total} = R_1 + R_2 + R_3 + \cdots + R_n$$

توجه کنید که مقاومت معادل یا کلی $$R_T$$ اثری مشابه ترکیب سری مقاومت‌ها در مدار را دارد و جمع جبری همه مقاومت‌های سری مدار است. اگر دو مقاومت یا امپدانس سری مقداری برابر داشته باشند، مقاومت معادل یا کلی آن ($$R_T$$) مقداری دو برابر مقاومت تکی یا $$2R$$ خواهد داشت. به همین ترتیب، سه مقاومت سری با مقدار مشابه، مقاومت معادلی برابر با $$3R$$ خواهد داشت.

شکل زیر این مسئله را نشان می‌دهد:

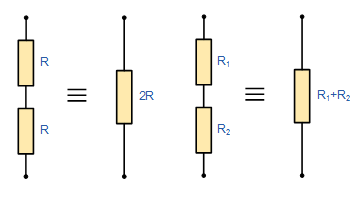
به همین ترتیب، اگر دو مقاومت یا امپدانس با مقادیری متفاوت و غیر برابر با یکدیگر سری باشند، مقدار معادل مقاومت ($$R_T$$) برابر با جمع ریاضی دو مقاومت ($$R_1+ R_2$$) خواهد بود. اگر سه مقاومت یا بیشتر داشته باشیم، مقاومت معادل آن برابر $$R_1 + R_2 + R_3+ \cdots$$ است. یک نکته مهم درباره مقاومت معادل این است که مقاومت معادل همواره از بزرگترین مقاومت در زنجیره مقداری بزرگتر دارد. از این مسئله می‌توان برای بازبینی مقاومت معادل محاسبه شده استفاده کرد. در مثال بالا، مقاومت معادل $$R_T = 9 k\Omega$$ است. در حالی که بزرگترین مقاومت زنجیره مقداری معادل $$6k \Omega$$ دارد.

ولتاژ مقاومت سری

ولتاژ بین دو سر هریک از مقاومت‌های زنجیره سری، از قوانینی متفاوت نسبت به جریان گذرنده از مقاومت‌ها تبعیت می‌کند. با مراجعه به شکل (۱)، مشاهده می‌شود که ولتاژ منبع با جمع افت ولتاژ ایجاده شده در مقاومت‌های $$R_1$$ و $$R_2$$ و $$R_3$$ برابر است. بنابراین:

$$V_{AB} = V_{R1} + V_{R2} + V_{R3} = 9V.$$

طبق قانون اهم، اختلاف پتانسیل ایجاد شده در مقاومت‌ها به صورت زیر محاسبه می‌شود:

$$R_1$$ اختلاف پتانسیل ایجاد شده در دو سر مقاومت = $$IR_1 = 1mA \times 1 k \Omega = 1V$$

$$R_۲$$ اختلاف پتانسیل ایجاد شده در دو سر مقاومت = $$IR_۲ = 1mA \times ۲ k \Omega = ۲V$$

$$R_۳$$ اختلاف پتانسیل ایجاد شده در دو سر مقاومت = $$IR_۳ = 1mA \times 6 k \Omega = 6V$$

به این ترتیب، افت ولتاژ کلی برابر است با:

$$V_{AB} = 1V + 2V + 6 V = 9V$$

که این مقدار، معادل ولتاژ منبع تغذیه است. جمع افت ولتاژ در دو سر هر یک از مقاومت‌ها با افت ولتاژ مقاومت معادل نیز برابر $$9V$$ یا همان ولتاژ منبع تغذیه است.

رابطه داده شده برای محاسبه افت ولتاژ کلی در مدار سری، جمع همه افت ولتاژهاست و به صورت زیر داده می‌شود:

$$V_{Total} = V_{R1} + V_{R_2} + V_{R3} + \cdots + V_N$$

این شبکه مقاومتی سری را می‌توان به صورت یک «تقسیم‌کننده ولتاژ» (Voltage Divider) نیز در نظر گرفت. به این ترتیب، یک مدار مقاومتی سری شامل N مولفه مقاومتی، N افت ولتاژ در هر مقاومت خواهد داشت.

با استفاده از قانون اهم می‌توان ولتاژ، جریان یا مقاومت هر شبکه مقاومتی سری را یافت. اگر مقاومت سری معادل با همه مقاومت‌ها جایگزین شود، جریان یا توان کلی در مدار تغییر نخواهد کرد.

مثال ۱

با استفاده از قانون اهم، مقاومت سری معادل، جریان سری، افت ولتاژ و توان تلف شده در هر یک از مقاومت‌ها را برای مدار شکل زیر بیابید:

حل: با استفاده از قانون اهم می‌توان این مسئله را حل کرد. جدول زیر مقدار جریان، ولتاژ و توان تلف شده در هر مقاومت را نشان می‌دهد:

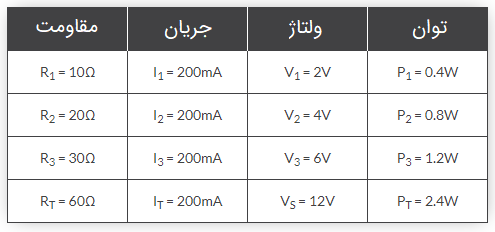
برای مدار داده شده در این مثال، $$R_T = 60 \Omega$$ و $$I_T = 200mA$$ و $$P_T = 2.4 W$$ است.

مدار تقسیم‌کننده ولتاژ

با مراجعه به مثال (۱) مشاهده می‌شود که افت ولتاژ در هر مقاومت مقداری متفاوت خواهد داشت. یکی از مزایای اتصال سری مقاومت‌ها با منبع تغذیه DC، استفاده از آن در تقسیم ولتاژ است. این مدار ساده، ولتاژ منبع را به تناسب میان مقاومت‌های زنجیره سری تقسیم می‌کند. مقدار افت ولتاژ در هر مقاومت، به مقدار مقاومت و جریان گذرنده از آن وابسته است.

می‌دانیم که در یک مدار سری، جریان گذرنده از همه مقاومت‌ها با یکدیگر برابر است. پس یک مقاومت با مقدار بزرگتر، افت ولتاژ بزرگتری ایجاد می‌کند. در حالی که افت ولتاژ در مقاومت کوچکتر، کمتر است.

مدار مقاومتی سری شکل (۱)، شبکه تقسیم‌کننده ولتاژ نام دارد. در این مدار، افت ولتاژهای $$2V$$ و $$4V$$ و $$6V$$ از منبع تغذیه ‍۱۲ ولتی ناشی می‌شوند. طبق قانون ولتاژ کیرشهف در یک مدار بسته، ولتاژ منبع با جمع همه افت ولتاژ‌ها یکسان است. طبق قانون تقسیم ولتاژ، می‌توان اختلاف پتانسیل در دو سر هر مقاومت را صرفنظر از جریان گذرنده از مدار سری محاسبه کرد. شکل زیر، مدار یک تقسیم‌کننده ولتاژ ساده را نشان می‌دهد:

دو مقاومت سری $$R_1$$ و $$R_2$$ در مدار شکل (۳)، به ولتاژ منبع $$V_{in}$$ متصل هستند. این منبع ولتاژ، از یک سو به مقاومت $$R_1$$ و از سوی دیگر به مقاومت $$R_2$$ متصل شده است و ولتاژ خروجی $$V_{out}$$ از دو سر این مقاومت گرفته می‌شود. رابطه زیر، ولتاژ در خروجی مدار را نشان می‌دهد:

$$V_{out}= V_{in} \left(  \frac{R_2}{R_1 + R_2}\right)$$

طبق قانون اهم با اضافه شدن مقاومت‌های سری در مدار، اختلاف پتانسیل‌های ایجاد شده در دو سر هر مقاومت، متفاوت و متناسب با مقدار مقاومت خواهد بود. در این حالت، جریان عبوری از آنها به دلیل بزرگتر شدن مقاومت معادل کمتر می‌شود. به همین دلیل، افت ولتاژ در مقاومت‌های قبلی کمتر خواهد شد.

پس اگر در مدار زنجیره سری سه مقاومت یا بیشتر داشته باشیم، همچنان می‌توان از رابطه تقسیم ولتاژ برای یافتن افت ولتاژ در هر مقاومت استفاده کرد. مدار زیر را در نظر بگیرید:

مدار تقسیم‌کننده ولتاژ در شکل (۴)، شامل چهار مقاومت سری است. اختلاف پتانسیل بین نقاط B و A به صورت زیر قابل محاسبه است:

$$V_{BA} = V_{R3} = V_s \times \frac{R_3}{R_1 + R_2 + R_3 + R_4}$$

$$V_{BA} = 10 \times \frac{30}{10+20+30+40} = 10 \times 0.3 = 3V$$

این ایده را می‌توان به یک گروه از مقاومت‌ها در مدار سری نیز اعمال کرد. برای مثال، اگر میخواستیم افت ولتاژ را در دوسر مقاومت‌های $$R_2$$ و $$R_3$$ محاسبه کنیم، جمع آنها را در صورت کسر رابطه تقسیم ولتاژ قرار می‌دادیم. در این حالت، افت ولتاژ ایجاد شده در مقاومت‌های $$R_2$$ و $$R_3$$ برابر ۵ ولت خواهد بود. زیرا:

$$V = V_s \times  \frac{R_2 + R_3}{R_1 + R_2 + R_3 + R_4} = 5 V $$

در این مثال ساده، مشاهده کردیم که افت ولتاژ در دو سر هر مقاومت با مقدار آن مقاومت و مقاومت معادل مدار متناسب است. مقاومت کلی مدار ($$R_T$$) در این مثال برابر $$100 \Omega$$ یا $$100 \%$$ است. افت ولتاژ در مقاومت $$R_1$$ برابر $$10 \%$$ مقاومت معادل است. پس $$10 \%$$ از ولتاژ منبع در دو سر آن ظاهر خواهد شد. به همین ترتیب، افت ولتاژ ایجاد شده در مقاومت $$R2$$ برابر $$20 \%$$ از ولتاژ منبع است. این مقدار برای مقاومت‌های $$R3$$ و $$R4$$ به ترتیب برابر $$30 \%$$ و $$40 \%$$ از ولتاژ منبع است. با اعمال قانون ولتاژ کیرشهف (KVL) در مسیر بسته، صحت محاسبات اثبات می‌شود.

حال فرض کنید بخواهیم یک مدار الکترونیکی را با استفاده از منبع ولتاژ بزرگ، تغذیه کنیم. مثلا فرض کنید که منبع ولتاژ ۱۲ ولتی است و مدار الکترونیکی فقط به ۶ ولت برای تغذیه احتیاج دارد و امپدانس ورودی آن ۵۰ اهم است. در این حالت باید از اصول تقسیم ولتاژ برای تغذیه این مدار الکترونیکی استفاده شود. دو مقاومت مشابه سری ۵۰ اهمی به منبع ولتاژ ۱۲ ولتی متصل می‌شوند. با اتصال یکی از مقاومت‌ها به مدار بار، خروجی مورد نظر ۶ ولتی در این مدار تقسیم‌کننده ولتاژ‌ ایجاد می‌شود. البته باید توجه داشت که امپدانس ورودی مدار الکترونیکی بی‌نهایت فرض شده است. مقاومت ورودی مدار الکترونیکی در این حالت، مقاومت متصل به منبع ولتاژ را تغییر می‌دهد. این مسئله، جریان کلی مدار و افت ولتاژ مقاومت‌ها را تغییر می‌دهد. پس می‌توان گفت که در استفاده از مدار تقسیم‌کننده ولتاژ، مقاومت ورودی مدار بار نیز بسیار مهم است. در ادامه با بیان یک مثال، این مسئله را واضح‌تر نشان می‌دهیم.

مثال ۲

در مدار شکل زیر، اختلاف ولتاژ بین نقاط X و Y را در دو حالت زیر بیابید:

• الف) $$R_L$$ متصل نیست.
• ب) $$R_L$$ متصل است.

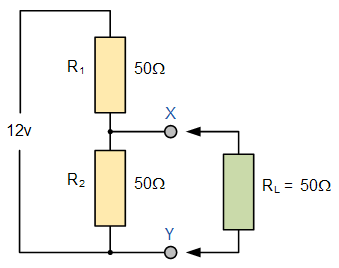
حل:

الف) در حالتی که مقاومت بار $$R_L$$ متصل نیست، خواهیم داشت:

$$R_{X-Y} = 50 \Omega$$

$$V_{out} = V_{in} \times \frac{R_2}{R_1 + R_2}$$

$$V_{out} = 12v \times \frac{50}{50+50} = 6.0 v$$

ب) در حالتی که مقاومت بار $$R_L$$ متصل است، دو مقاومت موازی خواهیم داشت. پس:

$$R_{X-Y} = 25 \Omega$$

$$V_{out} = V_{in} \times \frac {R_2}{R_1 + R_2}$$

$$V_{out} = 12v \times \frac{25}{50+25}= 4.0 v$$

 مطابق شکل (5) اگر بار به مدار متصل نباشد، ولتاژ خروجی $$V_{out}$$ برابر ۶ ولت خواهد شد. اما در حالتی که بار به مدار متصل است، ولتاژ خروجی به دلیل مقاومت‌های موازی برابر با ۴ ولت خواهد شد.

مشاهده می‌شود ولتاژ خروجی در اثر اتصال بار به شبکه تقسیم‌کننده ولتاژ تغییر می‌کند. زیرا ولتاژ خروجی بر اساس نسبت مقاومت‌های $$R_1$$ و $$R_2$$ تعیین می‌شود. هرچند، با افزایش مقاومت بار ($$R_L$$) به سمت بی‌نهایت ($$\infty$$) اثر بار کاهش می‌یابد. با اتصال مقاومت بار بی‌نهایت به شبکه تقسیم‌کننده ولتاژ، نسبت ولتاژ $$V_{out} / V_S$$ بدون تغییر خواهد ماند.

کاهش سطح ولتاژ یا سیگنال، «تضعیف» (Attenuation) نام دارد. از شبکه تقسیم‌کننده ولتاژ باید با احتیاط استفاده شود، زیرا مقاومت بار در خروجی بر عملکرد کل مدار تاثیرگذار است. اثر بار در خروجی مدار تقسیم‌کننده ولتاژ را می توان با استفاده از یک پتانسیومتر به جای مقاومت‌های ثابت و تنظیم صحیح آن جبران کرد. همچنین از این روش می‌توان برای جبران تلورانس در مقاومت‌های مدار تقسیم‌کننده ولتاژ استفاده کرد.

یک پتانسیومتر یا مقاومت متغیر که شامل هزاران مقاومت سری است، مثالی خوب از تقسیم‌کننده ولتاژ است. با اتصال یک ولتاژ ثابت به دو پایانه مدار می‌توان از خروجی پتانسیومتر، ولتاژ متغیر گرفت. هرچه پتانسیومتر تعداد دور بیشتری داشته باشد، کنترل ولتاژ در خروجی تقسیم‌کننده با دقت بیشتری انجام می‌شود. مدار تقسیم‌کننده ولتاژ ساده‌ترین راه برای تولید ولتاژ کوچکتر از ولتاژ بزرگتر است و اساس کار پتانسیومتر را تشکیل می‌دهد. علاوه بر تولید ولتاژ کوچکتر، از تقسیم‌کننده ولتاژ می‌توان برای تحلیل مدارهای مقاومتی پیچیده‌تر با انشعاب‌های موازی و سری، استفاده کرد. رابطه تقسیم ولتاژ برای محاسبه افت ولتاژ در یک شبکه DC و تحلیل مدار (قضایای کیرشهف یا تونن) استفاده می‌شود.

کاربردهای مقاومت سری

همانطور که مشاهده شد، از ساختار سری مقاومتی می‌توان در شبکه تقسیم‌کننده ولتاژ برای تولید ولتاژهای متفاوت استفاده کرد. اگر به جای یکی از مقاومت‌ها در مدار تقسیم‌کننده ولتاژ شکل (۵)، یک سنسور مثل ترمسیتور یا مقاومت وابسته به نور یا حتی یک کلید قرار گیرد، می‌توان از آن برای تبدیل یک کمیت آنالوگ به سیگنال الکتریکی قابل اندازه‌گیری استفاده کرد. برای مثال، شکل زیر مدار یک ترمسیتور را نشان می‌دهد:

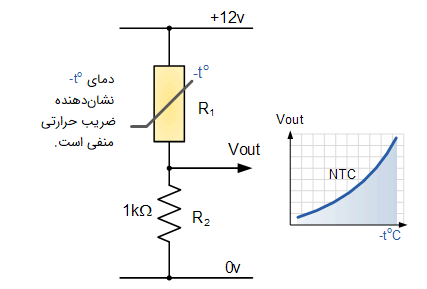
مقاومت این مدار در دمای $$25 ^ \circ$$ برابر $$10K \Omega$$ و در دمای $$100^ \circ C$$ برابر $$100 \Omega$$ است. ولتاژ خروجی ($$V_{out}$$) در این دو دما به صورت زیر محاسبه می‌شود:

•  در دمای $$25^ \circ C$$:

$$V_{out} = \frac{R_2}{R_1 + R_2 } \times V_{in}= \frac{1000}{10000+1000} \times 12 = 1.09v$$

• در دمای $$100 ^ \circ C$$:

$$V_{out} = \frac{R_2}{R_1 + R_2} \times V_{in}= \frac{1000}{100+1000} \times 12 = 10.9v$$

در این مدار با تغییر مقدار مقاومت ثابت $$R_2$$ و تبدیل آن به یک مقاومت متغیر یا پتانسیومتر، می‌توان به یک ولتاژ خروجی خاص رسید. محدوده دمایی بزرگتر، خاصیت این مدار است.

جمع‌بندی

هنگامی که دو یا چند مقاومت به طور پیوسته به یکدیگر متصل می‌شوند، مقاومت سری خواهیم داشت. مقاومت‌های سری، جریانی مشابه دارند اما افت ولتاژ در آنها یکسان نیست. زیرا طبق قانون اهم، علاوه بر جریان، مقدار مقاومت نیز عامل مهمی در افت ولتاژ محسوب می‌شود.

در شبکه مقاومتی سری، مقاومت‌ها با یکدیگر جمع می‌شوند و مقاومت سری معادل ($$R_T$$) را ایجاد می‌کنند. با تغییر محل مقاومت‌ها در مدار سری، مقدار جریان کلی برای هر یک از مقاومت‌های مدار تغییر نخواهد کرد. در آموزش بعدی راجع به مقاومت‌ها، به مقاومت‌های موازی خواهیم پرداخت. نشان خواهیم داد که در حالت اتصال موازی، بر خلاف مقاومت‌های سری که جریان‌ها برابرند، اختلاف پتانسیل بین دو سر همه مقاومت‌ها با یکدیگر برابر است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مدار‌های الکتریکی آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی برق
• مجموعه آموزش‌های مهندسی برق
• آموزش حل تمرین مدارهای الکتریکی 1
• مجموعه آموزش‌های دروس فیزیک
• جریان و مقاومت الکتریکی — از صفر تا صد