مقاومت موازی در مدار — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزشهای قبلی مجله فرادرس، درباره مقاومتها و انواع آن بحث کردیم. در این آموزش قصد داریم مقاومت موازی در مدارهای الکتریکی را بررسی کنیم. هنگامی که پایانههای چند مقاومت به هم متصل میشود، گفته میشود که این مقاومتها با یکدیگر «موازی» (Parallel) هستند. در یک شبکه مقاومتی موازی، بر خلاف مدار مقاومتی سری، جریان میتواند بیش از یک مسیر را انتخاب کند و از مسیرهای متفاوتی عبور کند. بنابراین میتوان گفت که مدار شبکه مقاومتی موازی، «تقسیمکننده جریان» (Current Divider) است.
جریان در هر یک از شاخههای مدار موازی، میتواند مقدار متفاوتی داشته باشد زیرا مسیرهای مختلفی برای عبور جریان وجود دارد. اما افت ولتاژ در همه مقاومتهای شبکه مقاومتی موازی، یکسان است. بنابراین مقاومتهای موازی، یک «ولتاژ مشترک» (Common Voltage) دارند و همه المانهای موازی نیز از این قاعده پیروی میکنند.
پس میتوان یک مدار مقاومتی موازی تعریف کرد که در آن، همه مقاومتها به دو نقطه یا گره مشخص متصل هستند. به این ترتیب، بیش از یک مسیر برای عبور جریان و یک منبع ولتاژ مشترک در مدار وجود دارد.
در مثال زیر سه مقاومت موازی با منبع ولتاژ را مشاهده میکنید. در این مثال، افت ولتاژ در مقاومت با افت ولتاژ در مقاومتهای و و با ولتاژ منبع برابر است. بنابراین، برای یک شبکه مقاومتی موازی، این ولتاژ مشترک به صورت زیر نوشته میشود:
مدار شکل زیر، سه مقاومت موازی و را نشان میدهد که بین نقاط A و B متصل شدهاند:
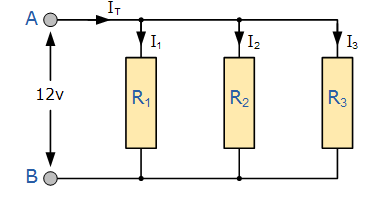
در آموزش مربوط به مقاومت سری دیدیم که در یک شبکه مقاومتی سری، مقاومت کلی مدار () برابر با جمع همه مقاومتهاست. برای مقاومتهای موازی، مقاومت معادل مدار () به روشی متفاوت محاسبه میشود.
در این حالت، مقدار معکوس مقاومتها () با هم جمع میشوند. این جمع برابر معکوس مقدار مقاومت معادل خواهد بود. رابطه مقاومت موازی معادل به صورت زیر است:
پس معکوس مقاومت معادل حاصل از دو یا چند مقاومت موازی، برابر با جمع مقدار معکوس هر یک از مقاومتهاست. اگر دو مقاومت یا امپدانس با مقدار یکسان به صورت موازی به هم وصل شوند، مقاومت معادل یا کلی () برابر با نصف مقدار یک مقاومت () خواهد بود. به همین ترتیب، برای سه مقاومت موازی با اندازه برابر، مقاومت معادل برابر با است.
ذکر این نکته ضروری است که مقاومت معادل در یک شبکه مقاومتی موازی همواره مقداری کمتر از کوچکترین مقاومت مدار دارد. پس با اضافه شدن مقاومت موازی به مدار، مقاومت کلی یا معادل کمتر میشود.
مقاومت موازی با مفهوم «رسانایی» (Conductance) مرتبط است. نماد کندوکتانس، G و واحد آن «زیمنس» (Siemens) است. مقدار کندوکتانس یک مقاومتی اهمی، معکوس مقدار مقاومت آن است. یعنی:
برای تبدیل رسانایی یا کندوکتانس به مقاومت، لازم است که معکوس کندوکتانس محاسبه شود. به این ترتیب، مقاومت معادل برای یک شبکه مقاومتی موازی محاسبه میشود. پس میتوان گفت که در یک شبکه مقاومتی موازی، رسانایی یک مقاومت با جمع رسانایی تک تک مقاومتها برابر است.
اکنون میدانیم که مقاومتهایی که بین دو گره مشابه در مدار قرار میگیرند، مقاومتهای موازی نامیده میشوند. اما یک مدار مقاومتی موازی علاوه بر مثال شکل (۱)، میتواند انواع دیگری نیز داشته باشد. شکل زیر، انواع روشهای اتصال مقاومتهای موازی را نشان میدهد:
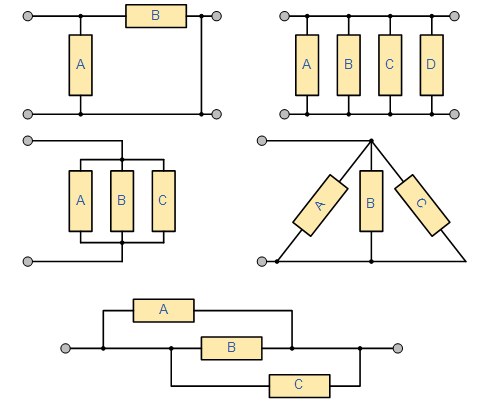
پنج شبکه مقاومتی نشان داده شده در شکل، ممکن است از نظر ظاهری متفاوت به نظر برسند، اما همه آنها شبکههای مقاومتی موازی هستند و به همین ترتیب شرایط و معادلات اعمال شده به آنها یکسان است. در ادامه با دو مثال، به بررسی مقاومتهای موازی میپردازیم.
مثال ۱
در شبکه موازی زیر، مقاومت کلی را بیابید:
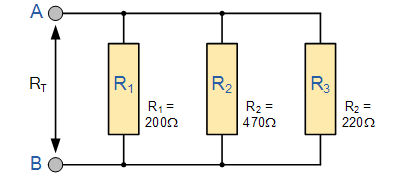
روش محاسبه معکوسهای مقاومتها را میتوان برای هر تعداد مقاومت در شبکه مقاومتی موازی تعمیم داد.
اگر فقط دو مقاومت موازی با یکدیگر داشته باشیم، رابطه محاسبه مقاومت معادل یا مقاومت کلی به صورت ساده زیر خواهد بود:
مثال ۲
مدار شکل زیر، یک شبکه شامل دو مقاومت موازی را نشان میدهد:
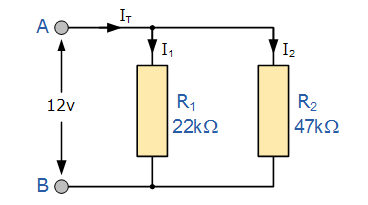
یک نکته مهم در محاسبه مقاومتهای موازی، این است که برای دو مقاومت موازی با هم، مقاومت معادل همواره مقداری کمتر از کوچکترین مقاومت مدار خواهد داشت. البته به یاد داشته باشید که این، یک شرط لازم است اما کافی نیست. یعنی اگر مقاومت معادل در یک شبکه مقاومتی موازی، مقداری کمتر از کوچکترین مقاومت مدار داشته باشد، الزاما نمیتوان گفت که مقاومت محاسبه شده صحیح است. اما اگر مقاومت محاسبه شده مقداری بیشتر از کوچکترین مقاومت مدار داشته باشد، میتوان گفت که در محاسبه مقاومت معادل حتما اشتباهی رخ داده است.
در مثال ساده بالا، و کوچکترین مقاومت مقداری معادل دارد. مشاهده میشود که مقاومت معادل یک شبکه موازی، مقداری کمتر از کوچکترین مقاومت مدار دارد. همچنین در صورتی که دو مقاومت و با هم برابر باشند، مقاومت معادل شبکه برابر نصف مقدار یکی از مقاومتها () خواهد بود. به همین ترتیب، اگر مقاومت موازی با مقدار مشابه داشته باشیم، مقاومت معادل آن برابر با خواهد بود که در آن مقدار یکی از مقاومتهاست.
برای مثال شش مقاومت ۱۰۰ اهمی را در نظر بگیرید که به صورت موازی به هم متصل شدهاند. مقاومت معادل این مقاومتها عبارت است از:
دقت کنید که این معادله، فقط برای مقاومتهای یکسان صحیح است و همه مقاومتها باید مقادیری مشابه داشته باشند.
جریان در مقاومت موازی
جریان کلی که به شبکه مقاومتی موازی وارد میشود، با مجموع همه جریانها در شاخههای موازی برابر است. همانطور که میدانیم مقدار جریان گذرنده از شاخههای موازی، الزاما یکسان نیست. جریان گذرنده از هر شاخه یا بازوی مدار با مقدار مقاومت در آن شاخه، متناسب است.
اگرچه همه شاخهها در یک شبکه موازی افت ولتاژ یکسانی دارند، اما مقدار مقاومت در این شاخهها میتواند به یک اندازه نباشد. بنابراین طبق قانون اهم، جریان گذرنده از هر مقاومت موازی، مقداری متفاوت دارد. مداری شامل دو مقاومت موازی را مانند مثال (۲) در نظر بگیرید. جریان گذرنده از این دو مقاومت در مدار، الزاما با هم برابر نیست و به مقدار هر مقاومت وابسته است. هرچند، میدانیم که جریان گذرنده از نقطه A با جریان گذرنده از نقطه B برابر است. یعنی مجموع این دو جریان در ابتدا و انتهای مدار با یکدیگر برابر است.
قانون جریان کیرشهف یا KCL بیان میکند: «جریان یا بار الکتریکی وارد شده به یک گره دقیقاً برابر با بار یا جریانی است که از آن خارج میشود و هیچ جریانی از بین نمیرود». بنابراین جریان کلی گذرنده از مدار به صورت زیر خواهد بود:
با استفاده از قانون اهم، جریان گذرنده از هر مقاومت در مثال (۲) را میتوان به صورت زیر محاسبه کرد:
جریان گذرنده از مقاومت =
جریان گذرنده از مقاومت =
بنابراین جریان کلی در مدار به صورت زیر خواهد بود:
البته با استفاده مستقیم از قانون اهم نیز میتوان به این نتیجه رسید:
جریان کلی گذرنده از یک مدار مقاومتی موازی برابر با جمع همه جریانهاست و به صورت زیر داده میشود:
از آنجا که در شبکههای مقاومتی موازی، جریان بین شاخههای مختلف تقسیم میشود، میتوان از آن به عنوان «تقسیمکننده جریان» (Current Divider) نیز استفاده کرد. پس جریان در یک مدار مقاومتی موازی که شامل N شاخه موازی است، N مسیر برای عبور دارد. ولتاژ در همه این شاخههای موازی با هم برابر است. با عوض کردن جای مقاومتها در یک شبکه موازی، مقاومت یا جریان کلی مدار تغییری نمیکند.
مثال ۳
جریان کل و جریان گذرنده از هر شاخه موازی را برای شبکه مقاومتی موازی زیر بیابید:
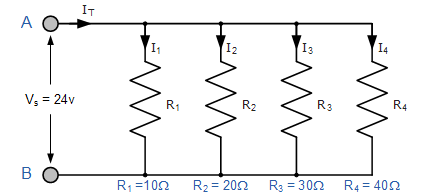
حل: از آنجا که منبع ولتاژ به صورت موازی به همه مقاومتها متصل شده است، میتوان از قانون اهم برای محاسبه جریان در هر شاخه این مدار استفاده کرد. پس داریم:
بنابراین جریان کلی برای مقاومتهای موازی به صورت زیر خواهد بود:
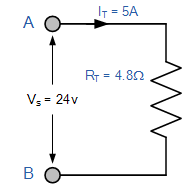
این جریان کلی را میتوان از طریق مقاومت معادل مدار مقاومتی موازی () و تقسیم آن به ولتاژ منبع نیز محاسبه کرد.
مقاومت معادل مدار به صورت زیر محاسبه میشود:
شکل زیر مقاومت معادل یک شبکه موازی را نشان میدهد:
جمعبندی
هنگامی که پایانههای چند مقاومت با هم مشترک باشد، گفته میشود که این عناصر با یکدیگر موازی هستند. همه مقاومتها در شبکه موازی، افت ولتاژ یکسانی را تجربه میکنند. اما جریان گذرنده از آنها یکسان نخواهد بود و طبق قانون اهم به مقدار مقاومتها بستگی دارد. بنابراین میتوان گفت که مدارهای موازی، تقسیمکننده جریان هستند. معکوس مقاومت کلی یا معادل ، با جمع معکوس همه مقاومتها برابر است. این مقاومت معادل همواره از کوچکترین مقاومت مدار، مقداری کمتر خواهد داشت. با تعویض جای المانهای شبکه مقاومتی موازی، مقدار کلی مقاومت یا جریان تغییری نخواهد کرد. اگر یکی از مقاومتها در شبکه مقاومتی موازی مدار باز شود، شبکه همچنان به کار خود ادامه خواهد داد.
میدانیم که توان تلف شده در هر مقاومت به صورت زیر محاسبه میشود:
از آنجا که در مدار موازی، ولتاژ در همه المانها یکسان است، پس هرچه اندازه مقاومت در یک مدار موازی بزرگتر باشد، توان تلف شده در آن کمتر است.
در صورت علاقهمندی به مباحث مرتبط در زمینه مدارهای الکتریکی آموزشهای زیر نیز برایتان مفید خواهد بود:
- مجموعه آموزشهای دروس مهندسی برق
- مجموعه آموزشهای مهندسی برق
- آموزش حل تمرین مدارهای الکتریکی 1
- مجموعه آموزشهای دروس فیزیک
- جریان و مقاومت الکتریکی — از صفر تا صد












سلام امید وارم سوال بنده را جواب دهید البته اینستاگرام هم پرسیدم بصورت تصویری راجب یک فرمولی هست که تازه دیدم نمیدونم چجوری محاسبه کنم
سلام جناب استاد ممنون از مطالب مفیدتون؛ من در برق مبتدی هستم ولی نوع بیان شما برایم قابل فهم بود؛ میشه لطف کنید و یک آموزش در مورد روشن کردن یک ال ای دی با برق ۲۲۰ ولت بیان بفرمایید بنده آموزش های اینترنت رو که دیدم متوجه شدم چندین روش برای این مساله است و می خواستم بدونم چرا هیچ کدوم از یک مقاومت ساده و ال ای دی برای این مدار استفاده نمی کنند و اکثرا از خازن هم در مدار استفاده می کنند برخی چند قطعه دیگه هم مثل دیود اضافه می کنند و سوال بعدیم اینه که مقاومت چه خصوصیتی داشته باشد به درد برق ۲۲۰ ولت بخوره و نسوزه؛ باز هم از شما سپاسگزارم.