آزمون تی دو نمونه مستقل – به زبان ساده

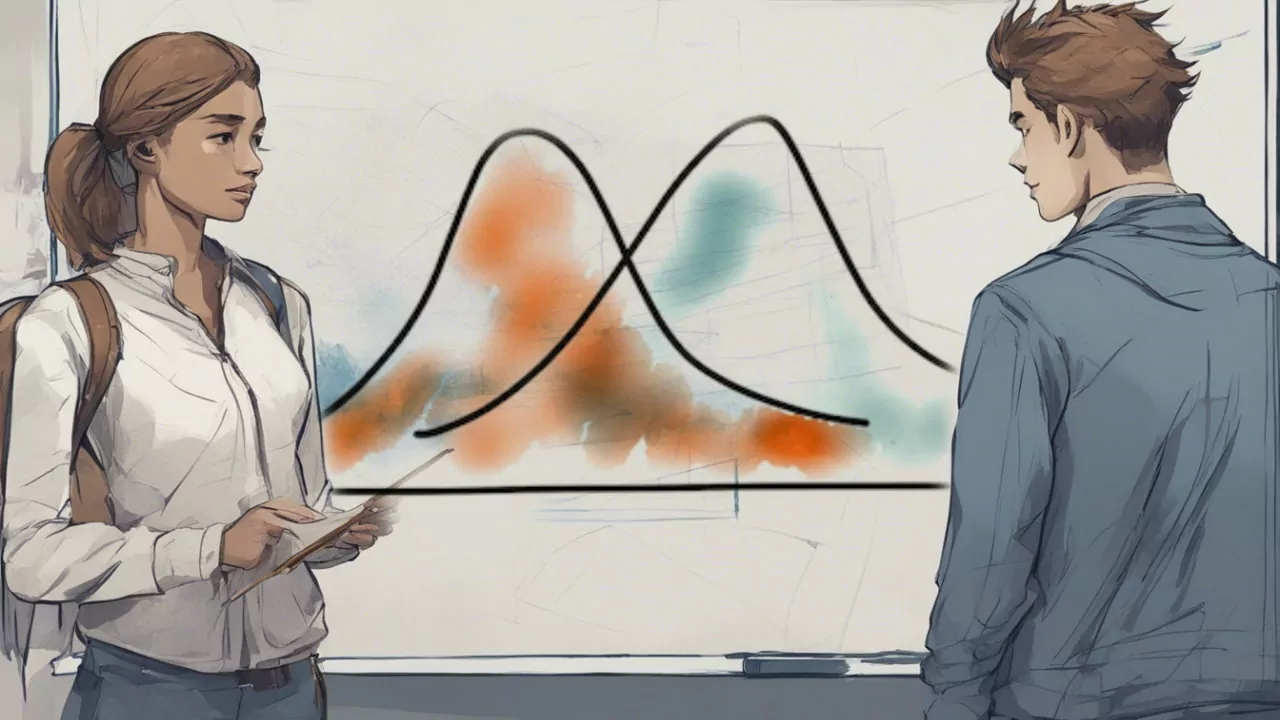
«آزمون مقایسه میانگین دو جامعه مستقل» (Independent Two Sample Mean Test)، یکی از آزمون‌های پر کاربرد در تحلیل‌های آماری است. به کمک این آزمون، می‌توانیم میانگین دو جامعه مستقل را با هم مقایسه کرده و نسبت به تفاوت آماری آن‌ها، تصمیم بگیریم. زمانی که داده‌های جوامع از توزیع نرمال پیروی کنند، آزمون و آماره تی برای مقایسه میانگین دو جامعه، مناسب است. ولی در زمانی که این توزیع مشخص نباشد، بهتر است از آزمون‌های ناپارامتری مشابه مانند‌ «آزمون من-ویتنی» (Mann-Whitney) استفاده کنیم. در این نوشتار به بررسی آزمون تی دو نمونه مستقل خواهیم پرداخت و شرایط و آماره‌های مورد نظر برای انجام این آزمون را مورد بررسی قرار می‌دهیم.

برای آنکه شواهد آماری مبنی بر اختلاف میانگین دو جامعه را محیا کنیم، از «آزمون تی دو نمونه مستقل» (Two Independent Samples t Test) استفاده می‌کنیم. این آزمون یک روش پارامتری محسوب شده و توزیع آماری هر دو جامعه نرمال فرض شده و با توجه به برآورد واریانس، از آماره‌ای با توزیع T‌ برای آزمون استفاده می‌کند.

نام‌های دیگر این آزمون در ادامه فهرست شده‌اند.

• آزمون T مستقل (Independent t Test)
• آزمون T اندازه‌های مستقل (Independent Measures t Test)
• آزمون T برای دو نمونه مستقل (Independent Two-sample t Test)
• آزمون T استیودنت (Student t Test)
• آزمون T دو نمونه‌ای (Two-Sample t Test)
• آزمون T امتیازات ناهمبسته (Uncorrelated Scores t Test)
• آزمون T غیر زوجی (Unpaired t Test)
• آزمون T غیر وابسته (Unrelated t Test)

نکته: این آزمون را نباید با «آزمون مقایسه زوجی» (Paired Sample T Test) اشتباه گرفت. در آزمون زوجی، مشاهدات در هر دو گروه به یکدیگر وابسته هستند.

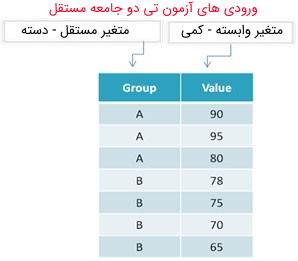
این آزمون در بیشتر نرم‌افزارهای محاسبات آماری، احتیاج به دو متغیر دارد. متغیر اول که همان متغیر آزمون محسوب می‌شود، شامل مقادیر کمی است که اغلب به آن «متغیر وابسته» (Dependent Variable) گفته می‌شود. هدف مقایسه میانگین این متغیر در بین دو گروه جداگانه است. به این ترتیب متغیر دوم، گروه‌ها یا دسته‌ها را مشخص می‌کند و در نتیجه باید یک متغیر کیفی یا ترتیبی باشد. در این آزمون این متغیر به «متغیر مستقل» (Independent Variable) معروف است. در نوشتار دیگری از مجله فرادرس از نرم‌افزارهای محاسبات آماری SPSS برای انجام این آزمون استفاده خواهیم کرد.

همانطور که در مقدمه ذکر شده، این آزمون در مواردی مانند استنباط‌های مطرح شده در فهرست زیر به کار می‌رود.

• بررسی اختلاف آماری بین میانگین دو گروه
• بررسی اختلاف آماری بین میانگین دو مداخله یا تیمار (Treatment-Intervention)
• بررسی اختلاف آماری بین میانگین دو گونه امتیاز (Score)

نکته: آزمون T دو نمونه مستقل، فقط برای دو نمونه یا گروه به کار می‌رود. اگر متغیر مستقل دارای بیش از دو سطح باشد، دیگر امکان به کارگیری این آزمون وجود ندارد و در این حالت باید از روش‌های «آنالیز واریانس» (ANOVA) کمک گرفت.

فرضیه‌های اولیه برای اجرای آزمون

قبل از انجام آزمون تی دو نمونه مستقل باید نسبت به فرضیه‌هایی که برای داده‌ها و شرایط آزمون وجود دارد، بررسی صورت بگیرد. در صورتی که این فرضیه‌ها به صورت تقریبی نیز برقرار باشند، باز هم می‌توان از آزمون تی دو نمونه استفاده کرد ولی در غیر اینصورت باید از روش‌های ناپارامتری برای مقایسه میانگین دو جامعه، بهره برد. این شرایط به صورت فهرست‌وار در ادامه معرفی شده‌اند.

• متغیر وابسته باید از نوع کمی (با مقیاس نسبی یا فاصله‌ای) باشد.
• متغیر مستقل یک متغیر کیفی (طبقه‌ای یا ترتیبی) یا دو سطح یا دو مقدار متفاوت است.
• مشاهدات باید هم برای متغیر وابسته و هم متغیر مستقل، دارای مقدار باشند. در حقیقت مشاهدات با مقدار گمشده برای هر یک از متغیرها، کنار گذاشته می‌شود.
• گروه‌های تشکیل شده توسط متغیر مستقل، باید نسبت به یکدیگر مستقل باشند، یعنی هیچ یک از مقادیر مثلا گروه اول نباید مقدارهای گروه دوم را تحت تاثیر قرار دهند.
• نمونه‌گیری و در نتیجه مشاهدات در هر دو گروه باید تصادفی باشند.
• در هر یک از سطوح متغیر مستقل، مقادیر متغیر وابسته باید از جامعه‌ای با توزیع نرمال، نمونه‌گیری شده باشند. خروج از توزیع نرمال و بخصوص «چولگی» (Skewness) زیاد برای این داده‌ها، باعث کاهش توان آزمون می‌شود. در صورت بزرگ بودن حجم نمونه و چولگی نامحسوس، باز هم استفاده از آزمون تی دو نمونه در صورت نرمال نبودن داده‌ّا، امکان‌پذیر است.
• واریانس در بین دو جامعه نرمال، باید یکسان یا تقریبا یکسان باشد. چنین ویژگی به عنوان «همسانی واریانس‌ها» (Homogeneity of Variances) شهرت دارد. این امر به آن علت است که بتوان نشان داد، تنها عامل تفاوت در بین دو جامعه، اختلاف در میانگین است. واضح است که هدف از اجرای آزمون نمایش این اختلاف است و اگر تفاوت، ناشی از شاخص دیگری از هر دو جامعه باشد، آزمون تی دو نمونه مستقل کارایی نخواهد داشت.
• در صورت نابرابری واریانس‌ها، بهتر است به جای آماره T از روش‌ها یا آماره‌های دیگر مانند «آماره ولچ» (Welch) کمک گرفت.
• مشاهدات نباید دارای «مقدار پرت» (Outlier) در متغیر وابسته باشند.

همانطور که در ابتدای متن نیز اشاره شد، در صورت برقرار نبودن هر یک از این شرایط یا فرض‌ها، نتایج آزمون تی دو نمونه مستقل نامعتبر شده و نمی‌توان به رای صحیح در مورد تساوی میانگین جامعه‌ها یا اختلاف میانگین در بین آن‌ها رسید. در چنین هنگامی اجرای آزمون ناپارامتری معادل، مانند آزمون «آزمون من-ویتنی» (Mann-Whitney) راه حلی مناسب محسوب می‌شود.

معمولا برای آنکه شرایط بهتری برای انجام آزمون تی دو نمونه مستقل فراهم شود، بعضی از محققین یکسان بودن تعداد مشاهدات در هر دو گروه را پیشنهاد می‌دهند. چنین شکلی از آزمون را «طرح متعادل» (Balanced Design) می‌نامند. همچنین داشتن حداقل ۶ مشاهده در هر گروه (به شرط داشتن توزیع نرمال) نیز از شرایطی محسوب می‌شود که برای اجرای آزمون تی دو نمونه مستقل لازم به نظر می‌رسد.

فرض‌های آماری در آزمون تی دو نمونه مستقل

فرض صفر و فرض مقابل برای آزمون تی دو نمونه مستقل به دو شکل نوشته می‌شود. البته هر دو حالت معادل هستند ولی آنچه در اکثر نرم‌افزارهای محاسبات آماری‌، به عنوان فرض صفر یا فرض مقابل در نظر گرفته می‌شود، شکل یا شیوه دوم در بیان فرض‌های آماری است. فرض کنید $$\mu_1$$، میانگین گروه اول برای متغیر وابسته و $$\mu_2$$ نیز میانگین گروه دوم باشد.

شیوه اول، به عنوان یک استاندارد در کتاب‌های آماری بازگو می‌شود.

$$\large H_0 : \;\; \mu_1 = \mu_2$$

$$\large H_1 : \;\; \mu_1 \neq \mu_2$$

ولی در شیوه دوم، مبنا برای اجرای آزمون، اختلاف میانگین‌های دو جامعه است. این شیوه در اکثر نرم‌افزارهای آماری برای بیان فرض‌های آماری در آزمون تی دو نمونه مستقل به کار می‌رود.

$$\large H_0 : \;\; \mu_1 - \mu_2 = 0$$

$$\large H_1 : \;\; \mu_1 - \mu_2 \neq 0$$

نکته: در نرم‌افزارهای آماری، در خروجی حاصل، یک فاصله اطمینان طبق فرض‌های معرفی شده در شیوه دوم برای اختلاف میانگین هر دو گروه ارائه می‌شود.

آماره آزمون

آزمون تی دو نمونه مستقل از یک آماره آزمون با توزیع t استفاده می‌کند. در نوشتارهای دیگر مجله فرادرس خواندید که آماره آزمون تی تک نمونه‌ای نیز دقیقا دارای توزیع t بوده و به شیوه‌ای ایجاد می‌شود که در ادامه خواهید دید.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

به یاد دارید که نسبت دو متغیر تصادفی مستقل، یکی با توزیع نرمال در صورت و دیگری با توزیع کای ۲ در مخرج، دارای «توزیع تی» (t-Distribution) است. در این حالت پارامترهای این توزیع، درجه آزادی مخرج (متغیر تصادفی با توزیع کای ۲) است.

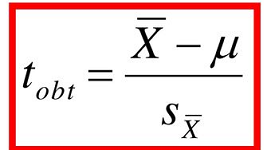
در اینجا هم از این ویژگی برای مشخص کردن آماره آزمون و توزیع آن استفاده می‌کنیم. انتظار داریم که اگر میانگین هر دو گروه از لحاظ آماری اختلاف معنی‌داری داشته باشند، فاصله استاندارد شده میانگین‌های نمونه‌ها، بزرگ باشد. پس آماره آزمون را به صورت زیر در نظر می‌گیریم.

$$\large Stat = \overline{X}_1 - \overline{X}_2$$

بهتر است ابتدا نمادها در فرمول‌های ارائه شده را برای ادامه کار، معرفی کنیم.

• $$n_1$$: تعداد نمونه‌ها از جامعه اول
• $$n_2$$: تعداد نمونه‌ها از جامعه دوم
• $$\overline{X}_1$$: میانگین نمونه‌ای از جامعه اول
• $$\overline{X}_2$$: میانگین نمونه‌ای از جامعه دوم
• $$S^2_1$$: واریانس نمونه‌ای از جامعه اول
• $$S^2_1$$: واریانس نمونه‌ای از جامعه دوم

آماره $$Stat$$ می‌تواند مفید باشد. به شرطی که توزیع آن را مشخص کنیم. از آنجایی که فرض بر این است که توزیع هر کدام از متغیرها (گروه‌ها) نرمال است، بهتر است ابتدا آن‌ها را به صورت استاندارد درآوریم تا توزیع بدون پارامتر شده و بتوانیم از آن به عنوان یک آماره آزمون یا کمیت محوری استفاده کنیم.

همانطور که می‌دانید برای تبدیل یک متغیر تصادفی با توزیع نرمال، به متغیر تصادفی با توزیع نرمال استاندارد، باید میانگین را از آن کم کرده و بر جذر واریانس آن متغیر تصادفی، تقسیم کنیم. از آنجایی که واریانس میانگین نمونه‌ای برابر است با $$\frac{\sigma^2}{n}$$ پس همین عملیات را روی آماره $$Stat$$ اجرا می‌کنیم. توجه داشته باشید که تحت فرض صفر، میانگین هر دو جامعه برابر است.

$$\large Stat = \dfrac{(\overline{X}_1 - \mu_1) - (\overline{X}_2 - \mu_2)}{S}$$

مشخص است که صورت به راحتی قابل محاسبه است. ولی مشکل بدست آوردن مخرج کسر است. واقعا واریانس اختلاف دو توزیع نرمال با میانگین یکسان چه خواهد بود. طبق شرط استقلال در دو جامعه داریم:

$$\large \text{Var}(\overline{X}_1 - \overline{X}_2) = \text{Var}(X_1) + \text{Var}(X_2)$$

برای محاسبه عبارت آخر، دو حالت را در نظر می‌گیریم. ۱- فرض برابری واریانس در هر دو گروه (Equal Variance Assumed) و ۲- فرض نابرابری واریانس گروه‌ها (Equal Variance Not Assumed).

آماره آزمون با شرط برابری واریانس‌ها

وضعیت اول را در نظر گرفته و برآوردی برای واریانس (یا انحراف معیار) اختلاف دو میانگین بدست می‌آوریم. با توجه به برابری واریانس‌ها می‌توانیم برآورد واریانس را برای اختلاف‌ها به صورت زیر محاسبه کنیم. مشخص است که برای همه مقادیر، مربعات فاصله از میانگین (‌با توجه به فرض صفر که برابری میانگین‌ها را نشان می‌دهد) حاصل شده است.

$$\large \sum( X_1 - X_2 )^2 = (n_1 - 1) S_1^2 + (n_2 - 1) S_2^2$$

و

$$\large \widehat{\text{Var}}( X_1 - X_2 ) = \dfrac{(n_1 - 1) S_1^2 + (n_2 - 1) S_2^2}{n_1 + n_2 - 2}$$

در نتیجه برای اختلاف میانگین‌ها خواهیم داشت:

$$\large \widehat{ \text{Var}} ( \overline{X}_1 - \overline{X}_2 ) = \dfrac{(n_1 - 1) S_1^2 + (n_2 - 1) S_2^2}{n_1 + n_2 - 2} \left( {\frac{1}{n_1} + \frac{1}{n_2}} \right)$$

رابطه بالا نشان دهنده محاسبه میانگین وزنی هر دو واریانس گروه‌ها برای محاسبه واریانس آمیخته است.

نکته: توجه داشته باشید که هر کدام از گروه‌ها دارای توزیع نرمال بوده و مستقل از هم هستند. در نتیجه کوواریانس صفر خواهد بود و خواهیم داشت:

$$\large \sum( X_1 - X_2 )^2 = \sum [ ( X_1 - \mu)+ (X_2 - \mu) ]^2 = \\ \large \sum [ ( X_1 - \mu_1)+(X_2 - \mu_2) ]^2 \overset{\small\mu_1 = \mu_2 } = \\ \large (n_1 - 1) S_1^2 + (n_2 - 1) S_2^2 + (n_1 + n_2 - 2) \text{Cov}(X_1, X_2)$$

که Cov همان کوواریانس بین دو متغیر است. پس با صفر بودن آن رابطه زیر بدست خواهد آمد.

$$\large \sum( X_1 - X_2 )^2 = (n_1 - 1) S_1^2 + (n_2 - 1) S_2^2$$

از آنجایی که دو میانگین برای این دو گروه برآورد شده و محاسبه واریانس نمونه‌ای صورت گرفته، درجه آزادی این واریانس نمونه‌ای برابر با $$n_1 - n_2 - 2$$ خواهد بود. پس با تقسیم رابطه بالا به درجه آزادی، برآوردگر واریانس حاصل می‌شود. این برآوردگر با نماد $$S^2_p$$ یا واریانس آمیخته (Pooled)، به این شکل نمایش داده شده و محاسبه می‌شود.

$$\large S^2_p= \dfrac{(n_1 - 1)S^2_1+ (n_2 - 1)S^2_2}{n_1 + n_2 - 2}$$

بنابراین آماره T را به صورت زیر خواهیم نوشت:

$$\large T = \dfrac{(\overline{X}_1 – \overline{X}_2) }{S_p (\sqrt{\frac{1}{n_1} + \frac{1}{n_2})}}$$

نکته: مخرج کسر بالا، همان انحراف استاندارد آمیخته برای تفاضل میانگین متغیرهای تصادفی هر دو گروه است. توجه داشته باشید که شیوه محاسباتی گفته شده، با شرط برابری واریانس در بین هر دو گروه است.

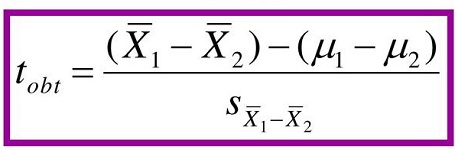
آماره آزمون با شرط نابرابری واریانس‌ها

همانطور که گفته شد، شرط استفاده از آزمون تی دو نمونه مستقل با توجه به برابری واریانس‌ها است. اگر این شرط برقرار نباشد، باید آماره آزمون را مورد بازنگری قرار دهیم. در این حالت آماره دیگری به کار گرفته می‌شود که در آن برآورد واریانس برای میانگین اختلاف‌ها، براساس مجموع واریانس هر یک از گروه‌ها خواهد بود.

در این صورت آماره آزمون به صورت زیر محاسبه می‌شود.

$$\large T = \dfrac{\overline{X}_1 - \overline{X}_2}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2} }}$$

درجه آزادی آماره T بدست آمده نیز طبق رابطه زیر مشخص خواهد شد.

$$\large df= \dfrac{ \left(\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}\right)^2}{\frac{1}{n_1 - 1}\left( \frac{S_1^2}{n_1} \right)^2 + \frac{1}{n_2 - 1}\left( \frac{S_2^2}{n_2} \right)^2}$$

در حالت کلی اگر مقدار آماره $$T$$، از مقدار بحرانی توزیع $$t$$ با درجه آزادی ذکر شده، در سطح خطای $$\alpha$$، بزرگتر باشد، فرض صفر یعنی برابری میانگین در بین دو جامعه رد می‌شود. در غیر این صورت دلیلی بر رد فرض صفر نخواهیم داشت.

بررسی فرض برابری واریانس‌ها

تا اینجا دو گونه آماره آزمون مربوط به مقایسه میانگین در بین دو جامعه مستقل مطرح و معرفی شد. ولی سوالی که باقی می‌ماند این است که از کدام یک از آن‌ها باید استفاده کنیم؟ پاسخ به این سوال در این قسمت مورد بحث قرار می‌گیرد. در حقیقت می‌خواهیم به کمک آزمون برابری واریانس‌ها نشان دهید که آیا باید از آماره آزمون نوع اول استفاده کنیم یا باید از نوع دوم آماره در آزمون تی دو نمونه مستقل استفاده کرد.

در اینجا برای نمایش برابری واریانس در بین دو جامعه از «آزمون لون» (Leven's Test) کمک می‌گیریم. فرض صفر و فرض مقابل برای چنین آزمونی به صورت زیر نوشته می‌شود.

$$\large H_0: \; \sigma^2_1 = \sigma^2_2$$

$$\large H_1: \; \sigma^2_1 \neq \sigma^2_2$$

آماره مورد نظر برای آزمون برابری واریانس‌ها در روش لون به صورت زیر نوشته می‌شود.

$$\large W = (n - 2) \cdot {\frac {\sum_{i = 1}^{2}n_{i}(Z_{i \cdot } - Z_{\cdot \cdot })^{2}}{\sum_{i = 1}^{2}\sum_{j = 1}^{n_{i}}(Z_{ij} - Z_{i\cdot })^{2}}}$$

اگر $$Z_{1j}$$ اختلاف مقادیر گروه اول با میانگین آن گروه و $$Z_{2j}$$ نیز اختلاف مقادیر گروه دوم از میانگین همان گروه را نشان دهند، آماره $$W$$ دارای «توزیع فیشر» (F Distribution) با $$n-2 , 1$$ درجه آزادی خواهد بود. در ضمن منظور از $$Z_{1\cdot}$$ و $$Z_{2\cdot}$$ میانگین مقادیر $$Z$$ در گروه اول و دوم است. همچنین $$Z_{\cdot \cdot}$$ میانگین کل گروه‌ها و $$n$$ نیز تعداد همه مشاهدات را نشان می‌دهد. واضح است که $$n_1$$ و $$n_2$$ نیز تعداد مشاهدات در گروه اول و دوم را تعیین کرده‌اند.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

به این ترتیب بزرگ بودن مقدار $$W$$، نشانگر نابرابری واریانس‌ها خواهد بود. کافی است که مقدار $$W$$ را با صدک $$\alpha$$ توزیع $$F$$ با درجه‌های آزادی $$1$$ و $$n-2$$ مقایسه کرد. در صورتی که $$W$$‌ بزرگتر از مقدار صدک باشد، فرض صفر رد می‌شود و در غیر اینصورت، فرض برابری واریانس‌ها در بین گروه‌ها مورد تایید قرار می‌گیرد. در نتیجه هنگام استفاده از آزمون تی دو نمونه مستقل مشخص می‌شود که از کدام آماره باید کمک گرفت و برآورد واریانس به چه شکل صورت می‌گیرد.

خلاصه و جمع‌بندی

همانطور که در این متن خواندید، یکی از روش‌های مقایسه دو جامعه و تشخیص تفاوت آن‌ها از یکدیگر، بررسی اختلاف میانگین آن‌ها توسط آزمون تی دو نمونه مستقل است. اگر میانگین‌ها در نمونه با یکدیگر اختلاف معنی‌داری داشته باشند، می‌توان نسبت به تفاوت هر دو جامعه رای داد. در صورتی که نمونه دلیلی بر وجود اختلاف آماری بین میانگین‌ها ارائه ندهد، فرض صفر رد نشده و می‌توان دو جامعه را مشابه در نظر گرفت. در نوشتارهای بعدی مجله فرادرس به نحوه اجرای این آزمون در نرم‌افزار محاسبات آماری SPSS خواهیم پرداخت.