وابستگی، کوواریانس و ضریب همبستگی در علم داده – راهنمای کاربردی
این نوشتار، قسمت چهارم از مطالب دنبالهدار در مورد نقش آمار در حوزه علم داده است که به موضوع و مبحث ضریب همبستگی و کاربرد آن در علم داده میپردازد. ضریب همبستگی یک شاخص دو بعدی است به این معنی که براساس دو متغیر محاسبه میشود. مقدار ضریب همبستگی میزان ارتباط بین دو متغیر را نشان میدهد. طی این مطلب به اهمیت محاسبه ضریب همبستگی اشاره کرده و البته برای نمایش ارتباط بین متغیرها از نمودارهایی نیز کمک خواهیم گرفت.


برای آشنایی با انواع روشهای محاسبه ضریب همبستگی، مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده را بخوانید. همچنین به منظور آشنایی با نحوه ترسیم نمودار نقطهای که در این متن به آن اشاره خواهیم داشت به نوشتار نمودار نقطه ای (Scatter Plot) در R — راهنمای کاربردی مراجعه کنید. البته خواندن متن رگرسیون خطی — مفهوم و محاسبات به زبان ساده خالی از لطف نیست.
قسمتهای مختلف این دنباله مقالات مطابق با فهرست زیر هستند.
- قسمت اول: شاخصهای آمار توصیفی در علم داده — راهنمای کاربردی
- قسمت دوم: توزیع های آماری مهم در علم داده — راهنمای کاربردی
- قسمت سوم: معیارهای مکانی و گشتاورها در علم داده — راهنمای کاربردی
- قسمت چهارم: وابستگی، کوواریانس و ضریب همبستگی — راهنمای کاربردی
- قسمت پنجم: احتمال شرطی، قضیه بیز (Bayes’s Theorem) — راهنمای کاربردی
ضریب همبستگی و کاربرد آن در علم داده
همانطور که اشاره شد، ضریب همبستگی شاخصی دو بعدی است. بنابراین برای محاسبه آن احتیاج به دو دسته داده (متغیر) داریم. همچنین برای نمایش ارتباط بین دو دسته داده میتوان از «نمودار نقطهای» یا «نمودار پراکندگی» (Scatter Plot) استفاده کرد. در این مطلب، با استفاده از ضریب همبستگی و البته رسم نمودار پراکندگی به بررسی وابستگی بین دو سری داده یا دو متغیر میپردازیم.
ابتدا براساس نمودار، ارتباط بین دو متغیر را نمایش داده و ارتباط بین شکل نمودار و ضریب همبستگی را مورد بررسی قرار میدهیم.
فرض کنید برای افرادی، میزان درآمد را به همراه سالهای تجربه کاری ثبت کردهایم. انتظار داریم که بین درآمد و تجربه کاری ارتباط و وابستگی وجود داشته باشد. به این معنی که با افزایش تجربه کاری، درآمد نیز افزایش یابد. براساس دادههای جمعآوری شده، نمودار پراکندگی ترسیم شده است که در ادامه قابل مشاهده است.
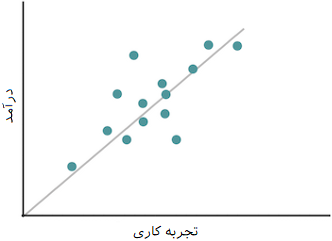
برطبق این نمودار مشخص است که با افزایش یا کاهش تجربه کاری میتوان میزان درآمد را حدس زد یا پیش بینی کرد. رابطه خطی بین این دو متغیر به خوبی در نمودار مشخص شده است. به این ترتیب میتوان از معادله این خط برای پیشبینی درآمد برحسب تجربه کاری استفاده کرد. هر چند این پیشبینی دارای خطا است ولی میتوان خط انتخابی را بوسیله روشهای رگرسیونی به شکلی انتخاب کرد که نسبت به هر خط دیگر، کمترین خطای ممکن را داشته باشد.
در مقابل اگر بین تجربه کاری و درآمد هیچ رابطهای وجود نداشته باشد، مشخص است که با افزایش تجربه کاری نمیتوان میزان درآمد را پیشبینی کرد. چنین وضعیتی در نموداری که در ادامه دیده میشود، ترسیم شده است.
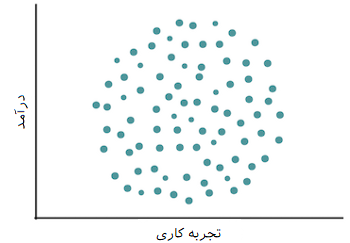
شاید استفاده از این نمودارها به منظور درک ارتباط بین دو متغیر مناسب باشد ولی نمیتوانیم با نگاه کردن به نمودارهای مشابه، به میزان ارتباط بین دو متغیر پیببریم. برای اندازهگیری میزان ارتباط خطی بین دو متغیر از «کوواریانس» (Covariance) و «ضریب همبستگی» (Correlation) استفاده خواهیم کرد.
کوواریانس (Covariance)
یک روش برای اندازهگیری میزان ارتباط بین دو متغیر، محاسبه کوواریانس بین آن دو است. همانطور که از اسم این معیار مشخص است، از ترکیب دو کلمه Co+Variance ساخته شده است. نحوه محاسبه کوواریانس به مانند محاسبه واریانس است با این تفاوت که به جای مجموع مربعات اختلاف از میانگین در واریانس، از مجموع حاصلضربهای اختلاف از میانگین هر دو متغیر در کوواریانس استفاده میشود.
به بیان دیگر همانطور که واریانس نشان میدهد یک سری داده چقدر از مرکزشان (میانگین) دور هستند، کوواریانس نشان میدهد که دو متغیر چقدر نسبت به یکدیگر تغییر میکنند. به این ترتیب میتوان کوواریانس را اندازه پراکندگی بین دو متغیر در نظر گرفت.
مقدار کوواریانس، ممکن است مثبت با منفی باشد. مقدارهای مثبت نشاندهنده وجود ارتباط مستقیم یا در یک جهت بین دو متغیر است. به این معنی که با افزایش یکی از متغیرها، دیگری نیز افزایش خواهد یافت یا اگر یکی از متغیرها کاهش داشته باشد، دیگری نیز کاهش مییابد. ولی اگر میزان کوواریانس منفی بدست آید، نشانگر وجود رابطه ولی در جهت عکس بین دو متغیر است. به این ترتیب اگر یکی از متغیرها به صورت صعودی تغییر کند، دیگری حتما به صورت نزولی خواهد بود.
اگر مقدار کوواریانس به صفر نزدیک باشد، نمیتوان رابطهی خطی بین دو متغیر در نظر گرفت. به این معنی که با افزایش یا کاهش یکی از متغیر، رفتار متغیر دیگر قابل پیشبینی نیست.
محاسبه کوواریانس
حال که به درستی نحوه تفسیر کوواریانس را فرا گرفتید، بهتر است شیوه محاسبه آن را نیز بیاموزید. مقدار کوواریانس بین دو متغیر و بوسیله رابطه زیر بدست میآید.
به نظر میرسد که میتوان این رابطه را به صورت ضرب داخلی دو بردار از مشاهدات نیز در نظر گرفت. برای محاسبه کوواریانس به صورت برداری کافی است که مراحل زیر طی شود.
- اختلاف درایههای هر بردار را نسبت به میانگین همان بردار محاسبه کنید.
- ضرب داخلی این دو بردار را محاسبه کنید. این کار در حقیقت به شکلی محاسبه کسینوس زاویه بین این دو بردار است. اگر جهت دو بردار مشابه یکدیگر باشد، مقدار کوواریانس به سمت مقدارهای بزرگ مثبت میل خواهد کرد. زیرا کسینوس زاویه بین دو بردار تقریبا برابر با ۱ خواهد بود. در صورتی که جهت دو بردار عکس یکدیگر باشد، کسیونس زاویه این دو بردار به سمت 1- میل کرده، در نتیجه کوواریانس به سمت مقدارهای کوچک منفی خواهد رفت.
- نتیجه حاصل شده از مرحله ۲ را بر تعداد مشاهدات () تقسیم کنید. البته اگر مقادیر مربوط به یک نمونه از جامعه آماری باشند باید نتیجه حاصل از مرحله ۲ را بر تقسیم کنید. به این ترتیب کوواریانس نمونهای بدست میآید.
نکته: از آنجایی که با دادههای حاصل از نمونهگیری مواجه هستیم، باید برای محاسبه کوواریانس، میانگین جامعه را هم برآورد کنیم. در نتیجه درجه آزادی صورت کسر، یک واحد کاهش خواهد داشت و در مخرج به جای از استفاده خواهیم کرد.
محدودیتهای کوواریانس
هر چند کوواریانس جهت ارتباط بین دو متغیر را به خوبی نشان میدهد ولی قادر نیست شدت ارتباط را محاسبه کند. در عمل واحد اندازهگیری دادهها میتواند در مقدار کوواریانس دخیل باشد. به این معنی که اگر واحد اندازهگیری دادههای درآمد را از هر دلار به ۱۰۰۰ دلار تغییر واحد دهیم، میزان کوواریانس به شدت تغییر میکند. از طرفی اگر واحد سنجش تجربه کاری را از سال به ماه تغییر دهیم، میزان کوواریانس ممکن است به شدت تحت تاثیر قرار گیرد و ۱۲ برابر شود.
به این علت برای مقایسه ارتباط بین دو گروه از متغیرها در دو جامعه مختلف (با مقیاسهای متفاوت) نمیتوان از کوواریانس استفاده کرد، مگر آنکه از دادههای استاندارد شده برای محاسبه کوواریانس استفاده کنیم. در چنین حالتی محاسبه کوواریانس برای این دادهها، ما را به ضریب همبستگی (Correlation) میرساند.
ضریب همبستگی (Correlation)
یکی از متداولترین معیارهای سنجش وابستگی بین متغیرها، ضریب همبستگی است که میزان و شدت ارتباط بین دو متغیر را نشان میدهد. همانطور که در قبل اشاره کردیم، ضریب همبستگی براساس دادههای استاندارد شده محاسبه میشود. به بیان دیگر ضریب همبستگی، نرمال شده کوواریانس محسوب میشود.
محاسبه ضریب همبستگی
معمولا ضریب همبستگی را با علامت (بخوانید رُو) نشان میدهند. شیوه محاسبه ضریب همبستگی مطابق را رابطه زیر است.
در اینجا منظور از و ، انحراف استاندارد و است. بوسیله نامساوی کوشی-شوارتز میتوان نشان داد که ضریب همبستگی در فاصله ۱- تا ۱+ تغییر میکند. بنابراین ضریب همبستگی یک شاخص نرمال شده از کوواریانس است.
علامت ضریب همبستگی مطابقت کاملا با علامت کوواریانس دارد. اگر دو متغیر دارای ضریب همبستگی مثبت و نزدیک یا برابر با ۱ باشند، شدت رابطه خطی بینشان زیاد است و تغییراتشان، در یک جهت است. در صورتی که مقدار ضریب همبستگی دو متغیر، منفی و نزدیک به ۱- باشد، شدت رابطه خطی زیاد ولی جهت تغییرات عکس یکدیگر خواهد بود.
اگر مقدار ضریب همبستگی به صفر نزدیک باشد، نمیتوان رابطه خطی بین دو متغیر در نظر گرفت. البته صفر بودن ضریب همبستگی دلیلی بر عدم رابطه بین دو متغیر نیست. برای مثال اگر باشد، میزان ضریب همبستگی بین دو متغیر ضعیف است در حالیکه مشخص است رابطه مشخص ریاضی ولی غیر خطی بینشان برقرار است.
ویژگیهای ضریب همبستگی
ضریب همبستگی علاوه بر مشخص کردن جهت رابطه بین دو متغیر، شدت یا میزان آن را هم نشان میدهد. از طرف دیگر با تغییر واحد اندازهگیری دادهها، ضریب همبستگی تغییر نکرده و در اندازهگیری شدت رابطه بین دو متغیر، تفاوتی ایجاد نمیشود. البته باید توجه داشت که بزرگ بودن قدر مطلق ضریب همبستگی، دلیلی بر وجود رابطه علت و معلولی بین دو متغیر نیست. در واقع این ضریب، وجود رابطه را مشخص میکند ولی نمیتوان یکی از متغیرها را معلول یا علت متغیر دیگر در نظر بگیرد. برای مشخص کردن متغیر علت یا معلول تنها راه استفاده از آزمایشهای کنترل شده است تا بوسیله ثابت نگه داشتن یک متغیر، تغییرات متغیر دیگر را اندازهگیری کرد تا تاثیر عوامل دیگر حذف شده و رابطه علت و معلولی قابل کشف شود.
نکته: شیوههای دیگری نیز برای اندازهگیری همبستگی یا وابستگی بین دو متغیر وجود دارد که بخصوص برای دادههایی که به صورت کیفی اندازهگیری میشوند، به کار گرفته میشوند. برای آشنایی با این روشها مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها را بخوانید.
در قسمت بعدی از سری مطالب به بررسی قانون یا «قضیه بیز» (Bayes’s Theorem) خواهیم پرداخت که بخصوص در علم دادهها، یکی از تکنیکهای پر کاربرد محسوب میشود.
اگر به فراگیری مباحث مشابه مطلب بالا علاقهمند هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای نرمافزارهای آماری
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها
- توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده
- امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها
^^













سلام توضیحاتتون عالی و سلیس بود،ممنون
ساده روان کاربردی. سپاسگزارم
سلام
خیلی ممنونم از بیان ساده و قابل فهم آموزش های شما
خداوند خیر و برکت بدهد به همه اساتید زحمتکش
سلام ودورد
یک سوال داشتم خدمتتون، با داشتن ماتریس کوواریانس و مقدار میانگین، شکل توزیع داده رو چطوری میشه ترسیم کرد
سلام، وقت شما بخیر؛
شکل توزیع دادهها با تابع چگالی مشخص میشود. برای شناسایی یک تابع چگالی در دست داشتن تابع مولد گشتاور یا تابع مشخصه لازم است. اگر مقدار گشتاور اول و دوم (میانگین و ماتریس کوواریانس) در اختیارتان باشد، نمیتوانید تابع مولد گشتاور را تولید کنید. به همین منظور ترسیم نمودار یا تشخیص توزیع دادهها میسر نخواهد بود.
از این که مسائل خود را با ما در میان میگذارید، سپاسگزاریم.
تندرست و پیروز باشید.
لطف شما بیکران نه در کران همبستگی 🙂
واقعا بی نظیر بود .خیلی ممنون از توضیح ساده و زیباتون
عالی بو. ممنون