ریشه دوم اعداد | محاسبه ریشه دوم در ریاضی — به زبان ساده

ریشه دوم اعداد یا جذر عدد، یک عمل ریاضی است که به کمک آن می‌توانیم اعداد مربع کامل را به صورت یک عدد درآوریم. هر چند جذر از عملیات پایه ریاضی (چهار عمل اصلی جمع، تفریق، ضرب و تقسیم) محسوب نمی‌شود ولی ترکیبی از آن‌ها است. در این نوشتار سعی داریم با ریشه دوم اعداد آشنا شده و کاربردهای آن را مورد توجه قرار دهیم. همچنین نحوه محاسبه ریشه دوم در ریاضی را با ذکر مثال‌های مختلف شرح دهیم. در این بین با استفاده از ماشین حساب و روش‌های ساده و دستی، سعی داریم به طور دقیق یا تقریبی، ریشه دوم اعداد را محاسبه کنیم. در انتهای متن با معرفی نرم‌افزار Maple‌ و آموزشی که فرادرس برای این نرم‌افزار ارائه داده است، شما را به فراگیری آن ترغیب خواهیم کرد تا به کمک آن قادر به حل مسائل ریاضی و حسابان باشید. با این کار، خواندن درس ریاضی و بخصوص حساب و حل تمرین‌های آن، تبدیل به یک عادت شده که از انجام آن لذت خواهید برد.

اگر احتیاج به یادآوری مطالب قبلی در مورد جذر دارید بهتر است نوشتارهای اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده و جذر یا محاسبه ریشه دوم عدد — به زبان ساده از مجله فرادرس را مطالعه کنید. همچنین خواندن مطالب معادله رادیکالی — به زبان ساده و قضیه فیثاغورس و کاربردهای آن — به زبان ساده که در آن‌ها از جذر و ریشه دوم اعداد استفاده می‌شود، نیز خالی از لطف نیست.

ریشه دوم اعداد

در ریاضیات، ریشه عددی مثل y برابر است با x اگر رابطه زیر برایشان برقرار باشد.

$$\large {\displaystyle y = x^2 }$$

رابطه ۱: توان و ریشه یابی

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

به عبارت دیگر، اگر $$x$$ را به توان دو برسانیم، به $$y$$ خواهیم رسید. می‌دانید که منظور از $$x^2$$، ضرب $$x$$ در خودش است که گاهی آن را مربع ایکس نیز می‌نامند. برای مثال ریشه ۴۹ برابر است با ۷ زیرا رابطه‌ فوق را برایشان می‌توانیم بنویسیم. به فرمول زیر دقت کنید.

$$\large {\displaystyle 4 9 = 7^2 }$$

واضح است که در اینجا $$x = 7$$ و $$y= 49$$ است. البته به این نکته نیز توجه کنید که ۷- نیز در رابطه بالا صادق است. به این معنی که حاصل یا ریشه معادله رابطه ۱، علاوه بر ۷، عدد ۷- نیز هست. به تساوی زیر توجه کنید.

$$\large {\displaystyle 4 9 = (- 7) ^2 }$$

در این حالت، ۷ و ۷- را ریشه‌های معادله گفته و ریشه مثبت را مقدار ریشه اصلی نامیده و ۷- را ریشه فرعی می‌گویند. گاهی نیز برای نمایش ریشه‌های معادله از شیوه نمایش $$\pm 7$$ بهره می‌برند.

نکته: ریشه اصلی را گاهی نتیجه محاسبه رادیکال ۴۹ نیز می‌گویند و به صورت زیر نمایش می‌دهند.

$$\large {\displaystyle \sqrt{4 9} = 7 }$$

به همین ترتیب می‌توان به عنوان مثال، ریشه‌های دوم یا رادیکال ۳۶، ۲۵ و ۱۴۴ را مشخص کرد.

$$\large {\displaystyle \sqrt{3 6} = 6 }$$

$$\large {\displaystyle \sqrt{2 5} = 5 }$$

$$\large {\displaystyle \sqrt{1 4 4} = 1 2 }$$

همچنین روش دیگر برای نمایش رادیکال، استفاده از توان است. به این ترتیب تساوی‌های مربوط به مثال‌های بالا را به صورت زیر نیز نمایش می‌دهند.

$$\large {\displaystyle {3 6}^{ \tfrac{ 1}{ 2} }= 6 }$$

$$\large {\displaystyle {2 5}^{ \tfrac{ 1}{ 2} }= 5 }$$

$$\large {\displaystyle {1 4 4}^{ \tfrac{ 1}{ 2} }= 1 2 }$$

برای این کار کافی است که طرف راست هر یک از تساوی‌های بالا را به توان ۲ رسانده و با مقدار سمت چپ، مقایسه کنید. واضح است که در این حالت، تساوی‌های زیر برقرار خواهند بود.

$$\large {\displaystyle 3 6  = 6^2 }$$

$$\large {\displaystyle 2 5 = 5^2 }$$

$$\large {\displaystyle 1 4 4 = 1 2^2 }$$

تا اینجا مشخص شد که برای اعداد مثبت می‌توانیم ریشه اصلی یا فرعی را محاسبه کنیم ولی ریشه‌های دوم اعداد منفی را نمی‌توان در گروه اعداد حقیقی جای داد. ریشه یا جذر دوم یک عدد منفی، در چارچوب اعداد مختلط مورد بحث قرار می‌گیرید. به طور کلی، ریشه‌ها یا توان رسانی را می‌توان در هر زمینه‌ای در نظر گرفت و برای هر مفهومی در ریاضی، از اصطلاح مربع یا حتی مکعب استفاده کرد. برای مثال توجه داشته باشید که در جبر ماتریس‌ها، به توان رساندن ماتریس‌ها نیز در ریاضی امکان‌پذیر است.

تاریخچه ریشه دوم اعداد و جذر

لوح سفالی بابِل (Yale Babylonian Collection YBC 7289) بین سالهای 1800 قبل از میلاد تا 1600 سال قبل از میلاد ایجاد شده است که در آن دو عدد $${\displaystyle {\sqrt {2} }}$$ و $${\displaystyle \dfrac{1}{\sqrt {2}}}$$ را نشان می‌دهد. مقادیر بدست آمده برمبنای ۶۰ برای هر یک از محاسبات گفته شده به ترتیب 1;24,51,10 و 0;42,25,35 است. توجه داشته باشید که نمایش اعداد برمبنای ۱۰ یا اعشاری (شیوه‌ای که امروزه برای دستگاه اعداد به کار می‌رود) و مبنای ۶۰ (شیوه عدد نویسی قدیمی) متفاوت است.

همچنین در یک قطعه پاپیروس (Papyrus Mathematical Papyrus) که نسخه‌ای مربوط به سال‌های 1650 قبل از میلاد است - احتمالاً «پاپیروس کهان» (Kahun)- نحوه محاسبه ریشه‌های دوم اعداد به کمک نسبت معکوس مشخص و برای چند عدد، مقدار آن محاسبه شده است.

در هند باستان، دانش نظری و کاربردی ریشه دوم یا جذر حداقل با قدمت حدود 800-500 سال قبل از میلاد مسیح است. آن‌ها روشی برای یافتن تقریب‌های بسیار خوب ریشه‌های دوم و سوم (جذر و رادیکال با فرجه ۳) در کتاب مقدسشان به نام Baudhayana Sulba Sutra آورد‌ه‌اند که هنوز نیز به کار می‌رود. حتی Aryabhata در کتاب خود به نام Aryabhatiya، روشی را برای یافتن ریشه مربع اعداد با تعداد زیادی رقم، ارائه داده است.

برای یونانیان باستان مشخص بود که ریشه‌های دوم اعداد صحیح مثبت که مربع های کاملی نیستند، همیشه اعداد غیر گویا هستند. می‌دانید که اعداد گویا اعدادی هستند که به واسطه نسبت دو عدد صحیح قابل نمایش هستند و در مقابل، اعداد غیرگویا، قابلیت ارائه توسط کسری از اعداد صحیح را ندارند. به بیان دیگر اعداد غیرگویا را نمی‌توان دقیقاً به صورت کسر به صورت $$\dfrac{m}{n}$$ نوشت که هر دو m و n عدد صحیح باشند. این موضوع مربوط به قضیه نهم اقلیدس است که به حدود 380 سال قبل از میلاد بر می‌گردد. فرض بر این است که حالت خاص ریشه دوم عدد 2 مربوط به اوایل کارها و فعالیت فیثاغورث است. او توانست نشان دهد که که دقیقاً طول قطر مربعی با طول ضلع ۱، برابر با رادیکال ۲ است. در کتاب‌های ریاضیات مردمان چین، که بین سالهای 202 قبل از میلاد و 186 قبل از میلاد در اوایل سلسله هان نوشته شده است، ریشه مربع یا ریشه دوم با استفاده از روش بیشینه یا کمینه‌سازی تقریبی صورت گرفته است.

نکته: به یاد داشته باشید که در سال‌های بسیار دور، نحوه شمارش و عدد نویسی به جای سیستم ده دهی که امروزه به کار می‌رود، عدد نویسی برمبنای ۶۰ بوده که وابسته به زمان و ساعت است. به همین جهت محاسبات آن‌ها نیز برمبنای ۶۰ صورت گرفته است.

علامت «√» برای نمایش ریشه مربع اولین بار در سال 1525، توسط «کریستوف رودولف» (Christoph Rudolff)‌ مطرح و در کتاب جبر به کار برده شد. امروزه نیز از این نماد برای نمایش رادیکال استفاده کرده و ریشه دوم اعداد را براساس آن، نشان داده یا محاسبه می‌کنیم.

موارد استفاده از جذر یا ریشه دوم اعداد

در این بخش، ریشه دوم عدد را به صورت یک تابع در نظر بگیریم و براساس متغیر با مقادیر حقیقی که البته مثبت هستند، آن را رسم کنیم. ولی بهتر است ابتدا نگاهی به تابع مربع یا توان دوم بیاندازیم که معکوس تابع ریشه دوم خواهد بود. شکل این تابع به صورت زیر است.

$$\large {\displaystyle f (x) =  x^2   }$$

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

در تصویر زیر نمودار مربوطه به این تابع را مشاهده می‌کنید.

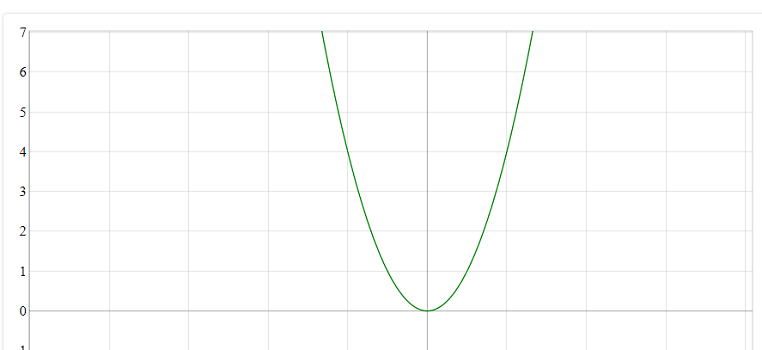
همانطور که در تصویر بالا مشاهده می‌کنید، دامنه این تابع، اعداد حقیقی و برد آن مقادیر مثبت است و در بازه اعداد منفی، نزولی و برای مقادیر مثبت متغیر، صعودی است. نقطه کمینه (کمترین مقدار تابع) نیز در نقطه‌ای با مختصات (۰ , ۰) رخ می‌دهد.

حال تابع ریشه دوم یا $$f(x) = \sqrt{ x}$$ را که معکوس تابع بالا است رسم می‌کنیم. به منظور مقایسه راحت‌تر هر دو تابع را در تصویر زیر، کنار هم رسم کرده‌ایم و هر یک را نام‌گذاری کرده‌ تا اشتباهی رخ ندهد.

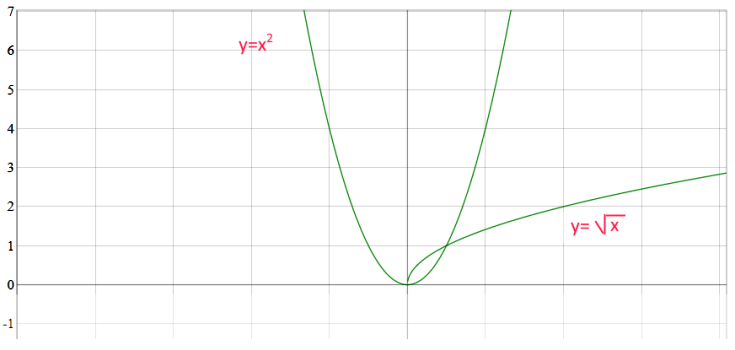
همانطور که می‌بینید، با توجه به مفهوم تابع معکوس، باید جای محورها را در نمودار اول تغییر داده تا معکوس تابع مشخص شود. البته می‌توان قرینه تابع توان دوم (مربع) را نسبت به نیمساز ربع اول ترسیم کرد تا معکوس تابع مشخص شود.

از آنجایی که تابع توان دوم، دارای بردی با مقادیر نامنفی است، دامنه معکوس آن یعنی ریشه دوم نیز فقط اعداد حقیقی مثبت به همراه صفر خواهد بود. به همین جهت هر دو تابع را در گروه توابع حقیقی در نظر می‌گیریم.

نکته: البته اگر با مجموعه اعداد مختلط مواجه باشیم، می‌توانیم این توابع را گسترش داده و در چنین فضای نیز به کار ببریم. در این حالت، ریشه دوم اعداد منفی نیز قابل تعریف و استفاده بوده و در گروه توابع مختلط در نظر گرفته می‌شوند. در ادامه مطلب به این موضوع نیز خواهیم پرداخت.

محاسبه ریشه دوم به کمک ماشین حساب

در اغلب ماشین حساب‌ها یک دکمه برای محاسبه ریشه دوم یا جذر عدد وجود دارد. در تصویر زیر یک نمونه ماشین حساب ساده را مشاهده می‌کنید که دکمه رادیکال در آن متمایز شده است. برای محاسبه ریشه دو اعداد آن‌ها را وارد کرده سپس دکمه رادیکال را فشار دهید.

برای مثال اگر بخواهیم ریشه دوم عدد ۴ را بدست آوریم، کافی است که پس از وارد کردن این عدد، دکمه رادیکال را فشرده تا در قسمت صفحه نمایش ماشین حساب، پاسخ (یعنی مقدار ۲) بدست آید. توجه داشته باشید که ماشین حساب‌ها، فقط ریشه اصلی (مقدار مثبت) را نشان می‌دهند و قادر به نمایش ریشه فرعی (منفی) نیستند.

البته اگر ماشین حساب شما دارای چنین دکمه‌ای نیست، باز هم می‌توانید ریشه دوم اعداد را محاسبه کنید. کافی است به خواندن متن ادامه دهید تا روش‌های پیدا کردن جذر اعداد به صورت تقریبی را بیاموزید. مقدار بدست آمده برای جذر اعداد به کمک روش‌های تقریبی دارای دقت مناسبی است که مشکلی برای محاسبات بعدی شما ایجاد نمی‌کند.

ریشه دوم اعداد مثبت و معادله درجه ۲

فرض کنید با یک معادله به صورت زیر مواجه هستیم:

$$\large {\displaystyle x^2 = 4 }$$

این معادله در حقیقت ریشه‌های دوم عدد ۴ را نشان می‌دهد. ریشه‌های این معادله، مقادیری هستند که اگر در جای متغیر ($$x$$) قرار گیرند، معادله یا تساوی برقرار خواهد بود. می‌دانیم این تساوی به ازاء دو مقدار $$x = -2$$ و $$x = 2$$ برقرار است. پس ریشه‌های دوم عدد ۴ به صورت ۲ و ۲- مشخص می‌شوند. ولی توجه داشته باشید که اگر منظور، پیدا کردن رادیکال ۴ است، که برابر با ریشه دوم ۴ در نظر گرفته می‌شود، باید مقدار ۲ مثبت را نشان دهیم، زیرا هرگز مقدار رادیکال منفی نخواهد بود.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

نکته: حل کردن یک معادله درجه دو با ریشه دوم یک عدد متفاوت است. این موضوع را در محاسبات ریاضی همیشه به یاد داشته باشید تا برد یا دامنه توابع را به درستی مشخص کنید.

به عنوان مثال‌های دیگر می‌توان به عدد ۴۹ و ۳۶ اشاره کرد که مربع کامل هستند. ریشه‌های دوم ۴۹ به صورت ۷ و ۷- مشخص می‌شوند. همچنین ریشه‌های دوم ۳۶ نیز به شکل ۶ و ۶- محاسبه می‌گردند. در ادامه به ریشه‌های دوم چند عدد دیگر اشاره کرده‌ایم. سمت راست تساوی‌ها، عدد و در سمت چپ، ریشه‌های دوم (اصلی و فرعی) را مشاهده می‌کنید.

$$\large {\displaystyle (- 3)^2 = 3^2 = 9 }$$

$$\large {\displaystyle (- 8)^2 = 8^2 = 6 4 }$$

$$\large {\displaystyle (-1 2)^2 = 12^2 = 1 4 4 }$$

$$\large {\displaystyle (-1 1)^2 = 1 1^2 = 1 2 1 }$$

به این ترتیب مشخص می‌شود که هر عدد مثبت، دو ریشه دوم دارد که قرینه یکدیگر هستند. ولی برای محاسبه رادیکال یک عدد، همیشه به قاعده زیر توجه داشته باشید.

$$ \large {\displaystyle \sqrt{ x^2} = \left| x \right| = \begin{cases} x, & \mbox{ if } x \ge 0 \\ -x, & \mbox{ if } x < 0 \end{cases} }$$

رابطه ۲: رادیکال و ریشه دوم اعداد

که در آن منظور از $$|x|$$ همان تابع قدرمطلق است. همانطور که مشاهده می‌کنید، اگر مقدار $$x$$‌ مثبت باشد، همان مقدار را در نظر می‌گیریم و اگر $$x$$ مقداری منفی باشد، قرینه آن یعنی $$-x$$ که مثبت است، در نظر گرفته می‌شود. به همین جهت، باید به مقادیر زیر و محاسبات صورت گرفته، توجه بیشتری کرد.

$$\large {\displaystyle \sqrt{ 9} = 3 }$$

$$\large {\displaystyle \sqrt{ 6 4} = 8 }$$

$$\large {\displaystyle \sqrt{1 4 4} = 1 2 }$$

$$\large {\displaystyle \sqrt{ 1 2 1} = 1 1 }$$

محاسبه ریشه دوم اعداد به کمک کسر معکوس

در این قسمت به کمک یک روش عددی و تقریبی ریشه دوم اعداد را محاسبه می‌کنیم. البته انتخاب دو نقطه به عنوان کران‌ها در دقت و تعیین مقدار مناسب برای جذر عدد مورد نظر بسیار اهمیت دارد.

فرض کنید عددی مانند $$x$$ دارید که می‌خواهید ریشه دوم آن را محاسبه کنید. باز هم در نظر بگیرید که عدد $$x$$ در بین دو عدد مربع کامل مثل $$a^2$$ و $$b^2$$ قرار دارد. به رابطه زیر دقت کنید که کران پایین و بالا برای $$x$$‌ را برحسب این اعداد مربع کامل نشان می‌دهد.

$$\large {\displaystyle a^2 < x < b^2 }$$

رابطه ۳: قرارگیری یک عدد در بین دو مربع کامل

بهتر است مقداری که برای $$a$$ و $$b$$ انتخاب می‌شود، نزدیک‌ترین اعداد مربع کامل به $$x$$ باشند. شاید انتخاب مقدار $$a$$ به عنوان ریشه دوم تقریبی عدد $$x$$، نتیجه خوبی داشته باشد. ولی بهتر است فاصله آن از مقدار $$x$$‌ را هم در نظر بگیریم. پس اگر خطای نسبی را براساس نصف فاصله این دو عدد نسبت به اندازه $$a$$ محسوب کنیم برای بدست آوردن ریشه دوم یا جذر عدد $$x$$ به فرمول زیر خواهیم رسید.

$$\large {\displaystyle \sqrt{ x} \approx a + \dfrac{ x - a^2}{ 2 a} }$$

پس برای مثال اگر بخواهیم ریشه دوم عدد ۲00 را به صورت تقریبی و سریع بدست آوریم، فرمول گفته شده را به ازاء مقدار $$a = 14 , b = 15, x = 200$$ بدست آورده و ریشه دوم 200 را مشخص می‌کنیم. واضح است که مربع یا توان دوم اعداد ۱۵ و ۱۴، نزدیکترین مقدار مربع کامل به ۲۰۰ هستند.

$$\large {\displaystyle   1 4^2 = 1 9 6  < 2 0 0 < 2 2 5 = 1 5^2 }$$

$$\large {\displaystyle \sqrt{ 200} \approx 14 + \dfrac{ 2 0 0 - 1 9 6}{ 2 \times 1 4}  =}$$

$$\large {\displaystyle 1 4 + \dfrac{ 4}{ 4 8 } = 1 4 . 0 8 3 }$$

از طرفی مربع عدد ۱۴٫083 نیز برابر است با 198٫33 که اختلاف کمی با مقدار ۲۰۰ دارد.

نکته: خطای محاسبات فرمول گفته شده برای مقادیر کوچک بسیار زیاد است، زیرا خطای نسبی در این حالت بزرگ خواهد بود. هر چه عددی که برای ریشه دوم آن اقدام کرده‌اید، بزرگتر باشد، خطا نسبی، کمتر خواهد بود.

برای مثال بعدی ریشه دوم 24 را محاسبه می‌کنیم.

$$\large {\displaystyle   4^2 = 1 6  < 2 4 < 2 5 = 5^2 }$$

$$\large {\displaystyle \sqrt{ 2 4} \approx 4 + \dfrac{ 2 4 - 1 6}{ 2 \times 4}  =}$$

$$\large  {\displaystyle 4 + \dfrac{ 8}{ 8 } = 4 + 1 = 5 }$$

که با مقدار واقعی $$\sqrt{24}$$ یعنی ۴٫89 اختلاف زیادی دارد. در حقیقت به جای اینکه حدس اولیه ما ۴ برای ریشه باشد، بهتر بود که آن را ۵ در نظر می‌گرفتیم.

روشی که برای پیدا کردن تقریبی ریشه دوم اعداد بیان کردیم، نشان می‌دهد که غیر از اعداد مربع کامل، هیچ عدد صحیح مثبتی نمی‌توان پیدا کرد که ریشه دوم آن‌ها یک عدد گویا باشد. به بیان دیگر، تعریفی که برای اعداد غیرگویا یا گنگ بیان می‌شود بر همین مبنا است. بنابراین نمی‌توان چنین اعدادی را به عنوان اعداد اعشاری ختم شده یا به صورت دوره گردش نوشت. به همین دلیل نیز این اعداد را گنگ یا اصم نامیده و در دسته یا مجموعه اعداد گویا قرار نمی‌گیرند.

همانطور که اشاره کردیم، بیشتر ماشین حساب‌های جیبی، کلیدی به عنوان محاسبه ریشه دوم یا رادیکال دارند. صفحات گسترده رایانه‌ای و سایر نرم افزارها و زبان‌های برنامه‌نویسی نیز به طور مکرر برای محاسبه ریشه دوم استفاده می‌شوند. در ماشین حساب‌های جیبی، از تقریبی که به روش نیوتن شهرت دارد استفاده می‌شود و با یک حدس اولیه و طی کردن تعداد گام‌های مشخص، به نزدیک‌ترین جواب یا پاسخ می‌رسند.

ولی در نرم افزارها و برنامه‌های محاسباتی، از لگاریتم و توابع نمایی برای محاسبه ریشه دوم استفاده می‌کنند. به رابطه زیر توجه کنید.

$$\large {\displaystyle {\sqrt { a}} = e^{( \ln a) / 2} = 10^{( \log_{10} a) / 2 } }$$

رابطه ۳: محاسبه ریشه دوم اعداد به کمک لگاریتم و تابع نمایی

فیلم مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

می‌دانید که منظور از $$\ln$$‌ تابع لگاریتم طبیعی و $$\log_{10}$$ نیز لگاریتم برمبنای ۱۰ است. در جدول زیر، طبق رابطه بالا، ریشه دوم چند عدد را محاسبه کرده‌ایم.

به کمک روش سعی و خطا، می‌توان یک برآورد را برای $${\displaystyle {\sqrt {a}}}$$ مشخص کرد. کافی است برای حل معادله زیر اقدام کنید. در این حالت روش‌های ریشه‌یابی که در ریاضی به صورت عدد به کار می‌روند، موثر خواهند بود.

$$\large {\displaystyle (x - a )^{2} = 0 }$$

که در صورت استفاده از اتحاد مربع کامل، می‌توان آن را به معادله درجه دوم زیر تبدیل و با استفاده از روش‌های محاسبات عددی حل کرد.

$$\large {\displaystyle (x + a )^{ 2} = x^{ 2 } + 2 x a + a^{ 2} }$$

شاید رایج‌ترین روش تکراری یا الگوریتم محاسبه ریشه دوم با دست تکنیک‌هایی باشد که به «روش بابِلی» یا «روش هرون» معروف است. در روش هرون، تابع به صورت زیر در نظر گرفته می‌شود.

$$\large {\displaystyle x^2  - a = 0 }$$

اعداد بدون ریشه دوم

همانطور که می‌دانید، در مجموعه اعداد حقیقی، نمی‌توان برای ریشه دوم، اعداد منفی را به کار برد. به بیان دیگر رابطه زیر قابل تعریف نیست.

$$\large {\displaystyle \sqrt{ -x } , \;\; x \geq 0 }$$

ولی اگر مجموعه اعدادی که با آن‌ها سروکار داریم را گسترش دهیم و به مجموعه اعداد مختلط توجه کنیم، ریشه دوم برای اعداد منفی نیز قابل تعریف است. به رابطه زیر توجه کنید.

$$\large {\displaystyle {\sqrt { - x } } = i { \sqrt {x} } }$$

مشخص است که در رابطه بالا، منظور از $$i$$ مقداری است که مربع آن برابر با ۱ است. به این ترتیب به رابطه زیر خواهیم رسید.

$$\large {\displaystyle (i {\sqrt x })^{2} = i^{2 }({ \sqrt x} )^{2} = ( - 1 ) x = - x }$$

نکته: ریشه دوم عدد صفر برابر با صفر است. از طرفی عدد صفر فقط یک ریشه دوم دارد.

قواعد عملیات روی رادیکال یا ریشه دوم اعداد

برای جمع یا تفریق رادیکال‌ها یا ریشه دوم اعداد به جز محاسبه تقریبی آن‌ها، روشی دیگری وجود ندارد. بنابراین ابتدا باید مقدار رادیکال‌ها را بدست آورد، سپس عمل جمع یا تفریق را انجام داد.

فرض کنید $$a$$ و $$b$$ دو عدد هستند که ریشه‌های دوم آن‌ها را به صورت $$\sqrt{a}$$ و $$\sqrt{b}$$ مشخص کرده‌ایم. در این حالت برای جمع یا تفریق به رابطه زیر دقت کنید.

$$\large {\displaystyle \sqrt{ a \pm b} \neq \sqrt{ a} \pm \sqrt{ b} }$$

برای مثال دو عدد ۲۵ و ۱۶ را در نظر بگیرید که اعداد مربع کاملی هم هستند.

$$\large {\displaystyle \sqrt{ 41} = \sqrt{ 2 5 + 16} \neq \sqrt{ 25} +  \sqrt{ 1 6}  =}$$

$$\large {\displaystyle 5 + 4 = 9 }$$

یا

$$\large {\displaystyle \sqrt{ 2 5 - 1 6} = \sqrt{ 9}  \neq \sqrt{ 25} -  \sqrt{ 1 6} = 5 - 4 = 1 }$$

ولی برای ضرب و تقسیم اعداد رادیکالی یا ریشه‌های دوم، می‌توان روابط زیر را در نظر گرفت.

$$\large {\displaystyle \sqrt{ a \times b } = \sqrt {a} \times \sqrt{ b} }$$

$$\large {\displaystyle \sqrt{ \dfrac{ a}{ b }} = \dfrac{ \sqrt {a}}{ \sqrt{ b} }}$$

به عنوان مثال فرض کنید، $$a = 4$$ و $$b= 9$$ باشد. آنگاه روابط بالا به صورت زیر نوشته می‌شوند.

$$\large {\displaystyle \sqrt{ 4 \times 9 } = \sqrt{ 3 6} = 6  = \sqrt {4} \times \sqrt{ 9} }$$

$$\large {\displaystyle \sqrt{ \dfrac{ 4}{ 9 } }= \sqrt{ \dfrac{ 2^2}{ 3^2 }}= \dfrac{ \sqrt { 4}}{ \sqrt{ 9}}  = \dfrac{ 2}{ 3}}$$

همانطور که خواندید، ریشه دوم و جذر اعداد ارتباط نزدیکی با یکدیگر دارند و به همین جهت در اغلب موارد به جای یکدیگر به کار می‌روند. ولی باز هم تاکید می‌کنیم که برای هر عدد مثبت، دو ریشه دوم وجود دارد که قرینه یکدیگرند، یعنی یکی مثبت و دیگری منفی است. ولی مقدار رادیکال اعداد مثبت فقط یک مقدار است که البته مثبت هم خواهد بود.

خلاصه و جمع‌بندی

در ابتدای این متن از مجله فرادرس اشاره کردیم که ریشه دوم اعداد تاریخچه بسیار قدیمی داشته و از نیازهای محاسباتی بشر محسوب می‌شود. شکل‌هایی مانند مثلث و مربع نیاز به اندازه‌هایی دارند که ممکن است به مجموعه اعداد گویا تعلق نداشته باشند به همین جهت ظهور اعداد غیرگویا یا اصم، ناگزیر می‌شود. رادیکال‌ها که بخشی از اعداد اصم یا گنگ را تشکیل می‌دهند، اغلب برمبنای روش‌های هندسی معرفی و مشخص می‌گردند. در این متن با توجه به این موضوع، روابط محاسباتی برای رادیکال‌ها و ریشه دوم اعداد مورد بررسی قرار گرفت و با ذکر مثال‌هایی موضوع را روشن‌تر کردیم.

همچنین با اشاره به آموزشی از فرادرس، نرم‌افزار Maple‌ را معرفی کردیم. به کمک این نرم‌افزار قادر هستید بسیاری از محاسبات عددی و حتی محاسبات ضمنی (پارامتری) را با استفاده از نوشتن آن‌ها به شکل نمادهای علمی و ریاضی، انجام داده و نتیجه را با راه حل دستی خود مقایسه و اشکالات احتمالی را پیدا کنید. به این ترتیب درک بهتری نسبت به مفاهیم ریاضی مانند مشتق، تابع، معادله و حتی انتگرال بدست خواهید آورد و ریاضیات برایتان قابل لمس شده و درس حسابان، به یک درس شیرین تبدیل خواهد شد که مطالعه آن برایتان دلچسب خواهد بود.