الکترومغناطیس چیست؟ — به زبان ساده

اگر در مورد چگونگی دیدن محیط اطراف خود یا نحوه کنار هم قرار گرفتن اجزای یک ماده سوالی دارید، مطالعه الکترومغناطیس به شما کمک می‌کند. علت اینکه امکان دیدن محیط اطراف برای ما وجود دارد این است که چشم انسان قابلیت آشکارسازی برخی طول‌موج‌های «امواج الکترومغناطیسی» را دارد. در مقیاس اتمی نیز اکثر برهم‌کنش‌های بین اتم‌ها و مولکول‌ها از جنس «نیروهای الکترومغناطیسی» هستند. همان‌طور که از خود کلمه الکترومغناطیس مشخص است، این بخش از علم فیزیک دو بازوی اصلی به نام «الکتریسیته» و «مغناطیس» دارد. در الکترومغناطیس با مغناطیس تولید شده توسط جریان الکتریکی و برهم‌کنش بین میدان‌های الکتریکی و میدان‌های مغناطیسی کار داریم.

در این مطلب ابتدا سعی می‌کنیم به بررسی دو مفهوم پایه‌ الکترومغناطیس یعنی الکتریسیته و مغناطیس بپردازیم. سپس، با یادگیری کمیت‌هایی مانند «میدان الکترومغناطیسی»، «نیروی الکترومغناطیسی» و «القای الکترومغناطیسی» به درک عمیق‌تری از الکترومغناطیس دست خواهیم یافت.

الکترومغناطیس چیست؟

در الکترومغناطیس الکتریسیته و مغناطیس دو روی یک سکه هستند. جریان الکتریکی می‌تواند میدان مغناطیسی تولید کند و میدان مغناطیسی متغیر نیز می‌تواند جریان الکتریکی را القا کند. به عبارت دیگر، با کاربرد الکترومغناطیس می‌توانیم ماده را در حضور الکتریسیته، مغناطیسی کنیم. اگر بخواهیم مهم‌ترین عامل در برهم‌کنش‌های الکترومغناطیسی را تعیین کنیم، می‌توانیم به «بار الکتریکی» اشاره کنیم. در واقع هر ذره‌ای در جهان دارای یک خاصیت ویژه است و این خاصیت تعیین می‌کند که برهم‌کنش ذره با هر یک از چهار نیروی بنیادی چگونه باشد. همان‌طور که این خاصیت در مورد «نیروی گرانش» (Gravitational Force) جرم است، برای نیروی الکترومغناطیسی بار الکتریکی است.

فیلم آموزش فیزیک – پایه دوازدهم در فرادرس

کلیک کنید

پیش از پیدایش الکترومغناطیس گمان بر این بود که الکتریسیته و مغناطیس دو مفهوم کاملا جدا از هم هستند. اولین بار «هانس کریستین اورستد» (Hans Christian Oersted) با مشاهده تغییر جهت‌ قطب‌نمای مغناطیسی اطراف سیم حامل جریان، متوجه پدیده الکترومغناطیس شد. بعدها انتشار مقاله «جیمز کلرک ماکسول» (James Clerk Maxwell) با عنوان «شرحی بر الکتریسیته و مغناطیس» در گسترش ایده الکترومغناطیس موثر بود.

کارکردهای الکترومغناطیس

دو کارکرد مهم الکترومغناطیس به این صورت است:

• بارهای الکتریکی متحرک در فضای اطراف خود میدان مغناطیسی ایجاد می‌کنند.
• وقتی که میدان‌ مغناطیسی اطراف بارها تغییر می‌کند، بارهای الکتریکی متحرک یا الکتریسیته تولید می‌شود.

فیلم آموزش الکترومغناطیس 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

هر دو مورد الکترومغناطیس نامیده می‌شوند. یکی از نتایج مهم دیگر الکترومغناطیس پیوند آن با نور است. میدان‌های الکتریکی و مغناطیسی می‌توانند در قالب یک موج الکترومغناطیسی با سرعت یکسانی معادل سرعت نور منتشر شوند. همچنین فرمول‌بندی کامل قوانین الکترومغناطیس را می‌توانیم در قالب چهار «معادله ماکسول» (Maxwell’s Equations) خلاصه کنیم که در ادامه به آن خواهیم پرداخت.

الکترومغناطیس یکی از مهم‌ترین مباحث پایه در رشته فیزیک و مهندسی برق است. در این راستا می‌توانید با مراجعه به مجموعه آموزش الکترومغناطیس درس، تمرین، حل مثال و تست فرادرس، مباحث پایه و پیشرفته را یا بگیرید.

الکتریسیته

ساده‌ترین مثال کاربرد الکتریسیته در زندگی روزمره، روشن کردن یک لامپ است. با فشردن کلید، مدار بسته می‌شود. اختلاف پتانسیل اعمال شده از سوی منبع باعث حرکت الکترون‌‌‌ها در طول سیم و برقراری جریان الکتریکی می‌شود. در نهایت با تبدیل الکتریسیته به نور، لامپ روشن خواهد شد. پس الکتریسیته نوعی انرژی است که با حرکت الکترون‌ها حاصل می‌شود. از مزایای این نوع از انرژی در دسترس بودن، قابلیت تولید و انتقال آسان آن به فواصل دور است. همچنین سهولت تبدیل الکتریسته به سایر انرژی‌ها مانند نور، گرما و انرژی مکانیکی (حرکت) بسیار مفید است. اگر به اطراف خود دقت کنیم، می‌توانیم الکتریسیته را در قالب یکی از سه گروه زیر در نظر بگیریم:

• الکتریسیته دینامیک (حرکت الکترون‌ها در یک سیم رسانا)
• الکتریسیته استاتیک (جمع‌شدگی الکترون‌ها روی بخشی از یک ماده نارسانا)
• انرژی الکترومغناطیسی (انتشار از طریق امواج الکترومغناطیسی)

گروه سوم از پیوند الکتریسیته با مغناطیس ناشی می‌شود و موضوع بحث این مطلب است. در الکتریسیته با قوانین و مفاهیم مهمی مانند «اصل بقای بار» (Charge Conservation Principle)، «قانون کولن» (Coulomb's Law) و «قانون گاوس» (Gauss's Law) روبه‌رو می‌شویم که در ادامه بصورت مختصر به این موارد اشاره شده است.

اصل بقای بار

اصل بقای بار یکی از قوانین بنیادی در طبیعت است. طبق این اصل، بار الکتریکی کل یک سیستم ایزوله تغییری نمی‌کند، بدین معنا که وقتی بار مثبت اضافی در یک بخش از سیستم ایجاد شود، همزمان در جای دیگری از سیستم همان مقدار بار بصورت منفی تولید شده است.

فیلم آموزش فیزیک 2 – پایه یازدهم – مرور و حل تمرین در فرادرس

کلیک کنید

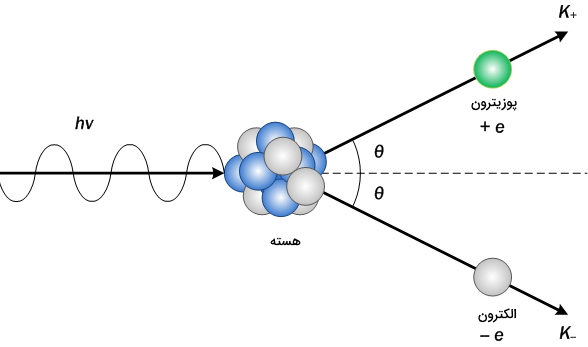
در طبیعت نیز این اصل رعایت می‌شود. برای مثال «تولید زوج» (Pair Production) که حاصل برهم‌کنش ماده و یک پرتو پرانرژی مانند اشعه گاما است. در این پدیده یک الکترون با بار منفی و یک پوزیترون با بار مثبت تولید می‌شود.

قانون کولن برای محاسبه نیروی الکتریکی

یکی از مهم‌ترین قوانین طبیعت که نیروی الکتریکی بین ذرات باردار را توصیف می‌کند، قانون کولن است. این قانون شباهت زیادی با قانون گرانش نیوتن دارد. اندازه نیروی الکتریکی که دو ذره باردار بهم وارد می‌کنند با مجذور فاصله بین هر دو ذره کاهش و با اندازه بار ذرات افزایش می‌یابد. جهت این نیرو با توجه به علامت ذرات باردار و ماهیت دافعه یا جاذبه بودن نیروها تعیین خواهد شد و راستای عمل آن در طول خط وصل کننده هر دو ذره است.

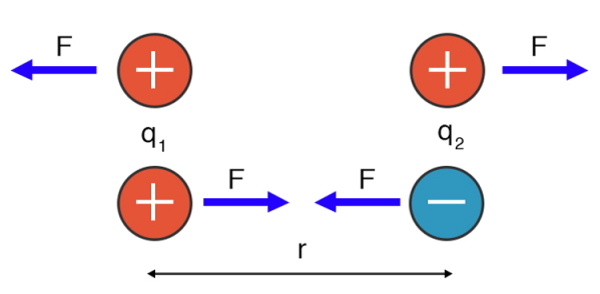
اگر این موارد را در قالب یک فرمول خلاصه کنیم، به رابطه زیر خواهیم رسید که در آن F اندازه نیروی الکتریکی، q اندازه بار الکتریکی هر ذره و r فاصله بین هر دو ذره باردار است:

$$F = { k q_1 q_2 \over r^2}$$

مقداری عددی ضریب k (ثابت کولن) در این رابطه برابر با k = 8.99×10⁹ (N.m²/C²) است.

قانون گاوس برای محاسبه میدان الکتریکی

در مبحث الکتریسیته مرسوم است که به‌جای بارهای الکتریکی، با میدان‌‌ الکتریکی کار داشته باشیم. برای مثال به این علت که بارها آزادانه در رسانا حرکت می‌کنند، نحوه توزیع بارهای الکتریکی در یک رسانا معمولا ناشناخته است. اما می‌دانیم مقدار میدان الکتریکی در یک رسانا در حالت تعادل صفر است. در واقع نیروی وارد شده به بارهای داخل رسانا به گونه‌ای چیدمان بارها را تغییر می‌‌‌‌‌دهند تا در نهایت میدان داخل رسانا صفر شود. در هر نقطه‌ای از فضا، اندازه میدان الکتریکی با اندازه نیروی الکتریکی وارد بر بار واحد برابر است.

طبق این تعریف، می‌توانیم برای فرمول‌بندی میدان الکتریکی از قانون کولن استفاده کنیم و با تقسیم آن بر بار واحد (q₀) اندازه میدان الکتریکی را بصورت زیر بدست آوریم:

$$E = {F \over q_0} = { k q \over r^2}$$

در این تعریف، هر ذره بارداری چه ساکن و چه در حال حرکت، می‌تواند در فضای اطراف خود میدان الکتریکی ایجاد کند. این پدیده موضوع قانون گاوس است. اگر بار ثانویه‌ای در این فضا قرار داده شود، این بار می‌تواند حضور میدان بار اولیه را حس کند. در واقع بار ثانویه با توجه به علامت خود به سمت ذره باردار اولیه جذب یا از آن دفع خواهد شد. قانون گاوس یکی از چهار معادله ماکسول است. بنابراین این قانون جزء قوانین اصلی الکترومغناطیس محسوب می‌شود. اگر سطح بسته‌ای با مساحت A را در نظر بگیریم، این قانون رابطه بین کل بار الکتریکی محبوس در این سطح (q_in) با میدان الکتریکی (E) را به‌صورت زیر ارائه می‌دهد:

مغناطیس

نکته جالب و مهم در مورد نحوه ایجاد مغناطیس این است که از حرکت بارهای الکتریکی تولید می‌شود. برای درک بهتر پدیده‌‌های مغناطیسی، مفاهیم این بخش را در مقایسه با مفاهیم معادل در الکتریسیته بررسی می‌کنیم. می‌دانیم نیروی دافعه یا جاذبه‌ای که دو آهنربا به هم وارد می‌کنند، از جنس مغناطیس است. اما برخلاف بار الکتریکی، تا امروز وجود بار مغناطیسی ثابت نشده است. فقط برخی از ذرات بنیادی دارای خاصیت مغناطیسی ذاتی به نام «گشتاور دوقطبی مغناطیسی» هستند. تقریبا می‌توانیم یک الکترون را به‌عنوان یک آهنربای میله‌ای کوچک در نظر بگیریم، زیرا حرکت الکترون‌های باردار دور هسته اتم نیز جریان کوچکی ایجاد می‌کند.

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

با این وجود در سطوح کاربردی برای ایجاد میدان‌های مغناطیسی لازم است از الکتریسیته استفاده کنیم و کاربرد مواد مغناطیسی به تنهایی چندان کمک‌کننده نیست. بنابراین پیوند الکتریسته و مغناطیس در ابتدایی‌ترین سطوح مطالعه در مورد میدان‌های مغناطیسی خود را نشان می‌دهد. همچنین خواهیم دید که مفاهیم میدان مغناطیسی و نیروهای مغناطیسی در مقایسه با همتای الکتریکی خود بسیار پیچیده‌تر‌ هستند. در ادامه به منظور درک بهتر تفاوت‌‌ها این موارد را جداگانه بررسی می‌کنیم.

تفاوت خطوط میدان

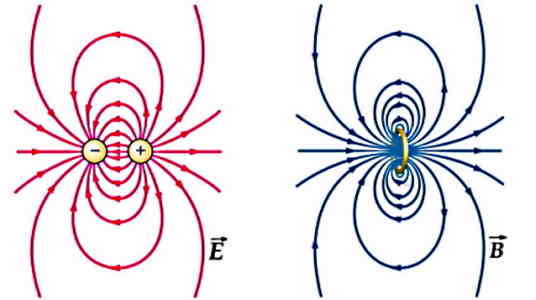
خطوط میدان الکتریکی همواره در راستای خط واصل ذره ایجادکننده میدان و نقطه موردبررسی هستند و از لحاظ جهت‌گیری، از بارهای مثبت شروع شده و به بارهای منفی ختم می‌شوند. اما برای خطوط میدان مغناطیسی نقطه شروع و پایانی وجود ندارد و این خطوط تشکیل یک حلقه بسته می‌دهند. در شکل زیر خطوط میدان الکتریکی برای دو بار مثبت و منفی با خطوط میدان مغناطیسی یک حلقه سیم دارای جریان الکتریکی مقایسه شده است. اگر در شکل بیشتر دقت کنیم متوجه خواهیم شد که راستای میدان مغناطیسی همواره عمود بر راستای حرکت ذره باردار ایجادکننده آن است.

نیروی مغناطیسی

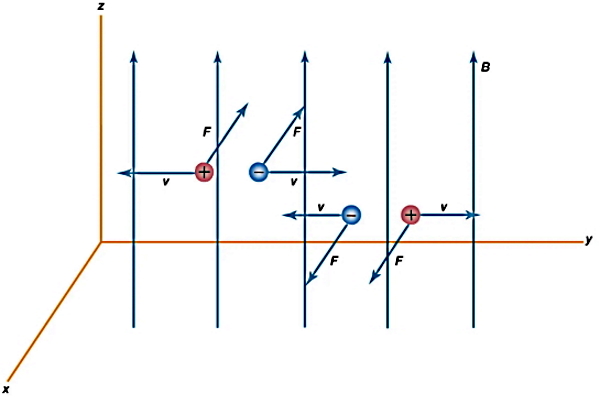
نیروهای مغناطیسی برخلاف نیروهای الکتریکی که توسط بارهای ساکن هم ایجاد می‌شدند، فقط به‌وسیله بارهای الکتریکی در حال حرکت تولید می‌شوند. در واقع اگر ذره باردار ساکن باشد، برهم‌کنشی وجود ندارد. اگر ذره باردار در حال حرکت با سرعت v باشد (مانند الکترون‌های در حال حرکت در یک سیم)، میزان برهم‌کنش به مقدار سرعت حرکت ذره وابسته است و به‌ شکل زیر خواهد بود:

$$\vec{F}= q \vec{v} \times \vec{B}$$

در این رابطه بار ذره با q، میدان مغناطیسی با B و نیروی مغناطیسی با F نشان داده شده است. همچنین با توجه به عملگر ضرب خارجی در فرمول، راستای نیروی مغناطیسی همواره بر راستای حرکت ذره باردار و میدان مغناطیسی، عمود است. در یک راستای حرکتی مشخص برای ذره باردار، بسته به علامت بار دو جهت‌گیری مخالف هم برای نیروی مغناطیسی خواهیم داشت.

قانون آمپر برای محاسبه میدان مغناطیسی

یک روش ساده برای تولید میدان مغناطیسی به این صورت است که اگر به یک سیم رسانا (مانند سیم مسی یا آلومینیمی) جریان الکتریکی اعمال شود، خود این جریان الکتریکی می‌تواند یک میدان مغناطیسی تولید کند. همانطور که گفتیم این پدیده برای اولین بار توسط اورستد نشان داده شد و «قانون آمپر» (Ampere's Law) توصیف کمی آن را نشان می‌دهد. همان‌طور که برای تعیین میدان الکتریکی از قانون گاوس استفاده می‌شد، برای محاسبه میدان مغناطیسی از قانون آمپر استفاده می‌شود.

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

پیش از توضیح این قانون، بهتر است ابتدا تعریف کنیم یک آمپر چقدر است. دو سیم بلند و نازک که موازی هم و در فاصله یک متری از هم در خلاء قرار دارند را در نظر بگیرید. اگر جریان عبوری از سیم‌ها هم‌جهت و برابر با هم باشد، طوری که نیروی وارد شده بر یک متر از هر سیم یک نیوتن باشد، در این صورت مقدار جریان عبوری از هر سیم یک آمپر است. این توضیح، تعریف آمپر در سیستم بین المللی یکاها است.

در مورد یک سیم بلند مستقیم، جهت میدان مغناطیسی به گونه‌ای است که سیم را در صفحه‌ای دایره‌‌ای شکل و عمود بر طول آن احاطه می‌کند. جهت چرخش حلقه‌‌های این میدان به جهت جریان عبوری از سیم بستگی دارد و با قاعده دست راست تعیین می‌شود. طبق این قانون اگر انگشت شست را در جهت جریان قرار دهیم، جهت قرارگیری سایر انگشتان نشان‌دهنده جهت میدان مغناطیسی است. برای مثال در شکل زیر یک سیم حامل جریان I_C را در نظر بگیرید. میدان B ایجاد شده توسط این سیم را می‌توانیم با در نظر گفتن مسیری به‌صورت حلقه بسته C که به آن «حلقه آمپری» (Amperian Loop) هم گفته می‌شود، بدست آوریم. با انتخاب المان طول dl از مسیر، قانون آمپر می‌شود:

$$\oint \vec{B} . d \vec{l} = \mu_0 I_{C}$$

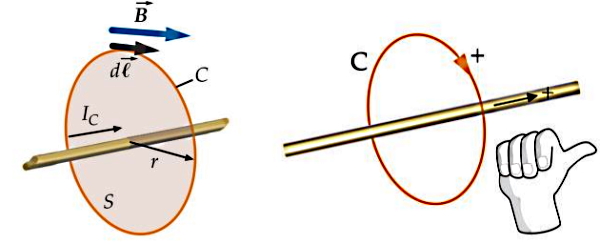
در این رابطه μ₀ نفوذپذیری خلاء (Permeability of Free Space) است و مقدار آن برابر است با μ₀ = 4π×10^-7 (T.m/A). اندازه میدان مغناطیسی با انتگرال‌گیری روی کل مسیر بسته بدست خواهد آمد. در ادامه کاربرد قانون آمپر و قانون دست راست را با حل دو مثال نشان می‌دهیم:

مثال ۱ برای قانون آمپر

میدان مغناطیسی داخل یک «سلونوئید» (Solenoid) با طول بی‌نهایت را پیدا کنید و نشان دهید این میدان یکنواخت (دارای اندازه ثابت) و در راستای محور استوانه است:

پاسخ

شکل زیر یک سلونوئید را نشان می‌دهد. برای استفاده از قانون آمپر لازم است ابتدا حلقه آمپری خود را طبق شکل طوری تعیین کنیم که بخشی از آن حتما داخل سلونوئید قرار بگیرد.

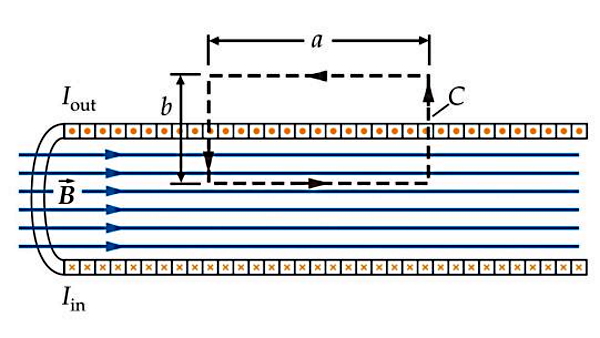
اگر فرض کنیم تعداد دورهای سیم در واحد طول n و جریان سیم برابر با I است، جریان کل عبوری از حلقه آمپری به طول a می‌شود:

$$I_C = nIa$$

طبق رابطه قانون آمپر برای حلقه مستطیل شکل خود، المان dl از صفر تا a تغییر می‌کند. پس نتیجه انتگرال خطی روی این المان a می شود و در نهایت داریم:

$$Ba = \mu_0nIa$$
$$B = \mu_0nI$$

بنابراین میدان داخل یک سلونوئید طویل برابر است با مقدار ثابت μ₀nI. مشخص است که اندازه میدان در تمام نقاط داخل سلونوئید، ثابت است و به مکان خاصی بستگی ندارد. برای تعیین جهت میدان لازم است انگشت شست دست راست خود را در راستای جریان قرار دهیم. در این شکل سطح مقطع سلونوئید نشان داده شده است که از قسمت پایین جریان وارد هر حلقه شده و از بالا خارج می شود. جهت جریان در حلقه آمپری به‌صورت عمود بر صفحه و به سمت بیرون است. بنابراین راستای سایر انگشتان دست در این حلقه از سمت چپ به راست خواهد بود. پس جهت میدان نیز مشخص شد که در راستای محور سلونوئید است.

مثال ۲ برای قانون آمپر

میدان مغناطیسی را برای داخل و خارج یک سیم بلند و مستقیم با شعاع R و جریان I حساب کنید:

پاسخ

ابتدا به بخش اول یعنی محاسبه میدان برای داخل سیم، پاسخ می‌دهیم. اگر مقطعی از سیم را به‌صورت شکل زیر در نظر بگیریم، انتخاب حلقه آمپری به‌صورت دایره نارنجی رنگ مناسب بنظر می‌رسد. در واقع چون میدان داخل سیم را می‌خواهیم، لازم است حلقه C را با شعاعی کوچکتر از شعاع سیم در نظر بگیریم (r<R). اگر یک المان طول dl را روی حلقه در نظر بگیریم، انتگرال خطی آن معادل با محیط حلقه خواهد شد، یعنی داریم:

$$\oint d \vec{l} =2\pi r$$

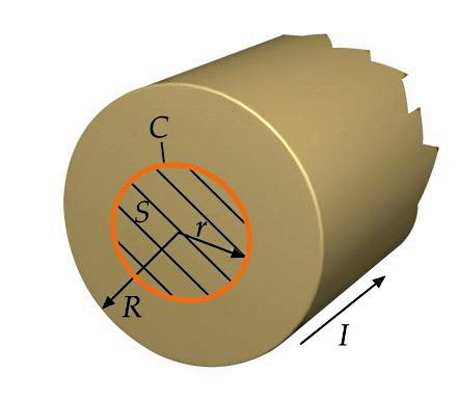
بنابراین طبق قانون آمپر خواهیم داشت:

$$\oint \vec{B} . d \vec{l} = B(2\pi r)= \mu_0 I_{C}$$

اما نکته مهم در اینجا این است که در فرمول قانون آمپر باید جریانی را قرار دهیم که داخل حلقه آمپری جاری است. در این مثال می‌دانیم جریان عبوری از کل مقطع سیم I است ولی جریان عبوری از مقطع معادل با حلقه را نمی‌دانیم و لازم است اول آن را محاسبه کنیم:

$$\frac{I_C}{I} = \frac{\pi r^2}{\pi R^2}$$

$$B(2\pi r)= \mu_0 I \frac{ r^2}{ R^2}$$

$$B= \frac{ \mu_0 I r}{ 2 \pi R^2}$$

پس میدان برای داخل سیم یعنی برای r<R برابر با مقدار بالا شد. به همین شکل می‌توانیم میدان را برای خارج از سیم محاسبه کنیم. در این حالت حلقه آمپری ما بزرگتر از مقطع سیم است و در نتیجه جریان مورد نظر در رابطه، معادل جریان کل سیم یعنی I است. پس برای R<r اندازه میدان می‌شود:

$$B(2\pi r)= \mu_0 I$$

$$B= \frac{ \mu_0 I}{ 2 \pi r}$$

میدان‌ الکترومغناطیسی

در الکترومغناطیس مستقل از حضور هر گونه بار خارجی، میدان‌های الکتریکی می‌توانند میدان‌های مغناطیسی را تولید کنند و برعکس. «مایکل فارادی» (Michael Faraday) برای اولین بار نشان داد چگونه یک میدان مغناطیسی متغیر با زمان می‌تواند یک میدان الکتریکی تولید کند و ماکسول نشان داد یک میدان الکتریکی متغیر با زمان نیز می‌تواند یک میدان مغناطیسی ایجاد کند. به‌علاوه ماکسول نشان داد میدان‌های الکتریکی و مغناطیسی در داخل فضا به‌صورت امواج الکترومغناطیسی با هم حرکت می‌کنند. بنابراین میدان الکترومغناطیسی یک میدان فیزیکی است که توسط ذرات باردار یا ذرات دارای گشتاور مغناطیسی ایجاد می‌شود.

خود میدان حامل بار الکتریکی یا گشتاور مغناطیسی نیست اما دارای انرژی و تکانه است. در واقع این میدان می‌تواند انرژی و تکانه خود را به ذرات باردار و ذرات دارای گشتاور مغناطیسی منتقل کند. گاهی این میدان می‌تواند ذرات را از بین ببرد یا ذره ایجاد کند. یک میدان الکترومغناطیسی همواره شامل دو مولفه جداناپذیر یک میدان الکتریکی و یک میدان مغناطیسی است.

بر این اساس، این میدان‌ها با توجه به جزئیات دو مولفه خود می‌توانند در یکی از پنج گروه زیر قرار داده شوند:

• میدان‌های الکترواستاتیک (Electrostatic Fields): شامل یک میدان الکتریکی استاتیکی و یک میدان مغناطیسی ناچیزاند (میدان اطراف یک بالن ثابت دارای بار استاتیکی)
• میدان‌های مگنتواستاتیک (Magnetostatic Fields): شامل یک میدان مغناطیسی استاتیکی و یک میدان الکتریکی ناچیزاند (میدان اطراف یک آهنربای ثابت)
• میدان‌های الکتروشبه‌استاتیک (Electroquasistatic Fields): شامل میدان‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌های الکتریکی و مغناطیسی به کندی متغیر با زمان که مولفه میدان الکتریکی غالب است (میدان داخل یک مدار الکتریکی ساده)
• میدان‌های مگنتوشبه‌استاتیک (Magnetoquasistatic Fields): شامل میدان‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌های الکتریکی و مغناطیسی به کندی متغیر با زمان که مولفه میدان مغناطیسی غالب است (میدان داخل یک ژنراتور الکترومکانیکی)
• امواج الکترومغناطیسی (Electromagnetic Waves): شامل میدان‌های الکتریکی و مغناطیسی به سرعت متغیر با زمان‌اند (امواج رادیویی)

قانون لورنتس برای محاسبه نیروی الکترومغناطیسی

در حال حاضر می‌دانیم که جهان ما بر اساس چهار نیروی اصلی کار می‌کند. در مقیاس‌ بالا مانند کهکشان‌ها نیروی غالب نیروی گرانش است. در مقیاس زیراتمی دو «نیروهای هسته‌ای قوی و ضعیف» (Strong and Weak Nuclear Forces) غالب‌اند. در هر مقیاسی بین این دو حد، نیروهای الکترومغناطیسی قرار می‌گیرند. مزیت کاربردی نیروهای الکترومغناطیسی این است که از نیروهای گرانشی قوی‌تراند و در عین حال برخلاف نیروهای هسته‌ای قوی و ضعیف محدوده اثر بی‌نهایت دارند. پس از توصیف میدان‌‌‌های الکترومغناطیسی، می‌خواهیم ٰبرهم‌کنش این میدان‌‌‌‌‌‌ها با ذرات باردار یا یک سیم حامل جریان را توسط قانون «نیروی لورنتس» (Lorentz Force) مطالعه کنیم.

طبق این قانون در حضور میدان‌‌‌های الکتریکی (E) و مغناطیسی (B) به هر ذره باردار q در حال حرکت با سرعت v یک نیروی پس و پیش از سمت میدان الکتریکی و یک نیروی جانبی از سمت میدان مغناطیسی وارد می‌شود. اگر این دو نیرو را در یک رابطه با هم جمع کنیم، می‌توانیم کل نیروی الکترومغناطیسی وارد بر ذره (F) را طبق قانون لورنتس بدست آوریم:

 $$\vec{F}= q (\vec{E} + \vec{v} \times \vec{B})$$

در این رابطه بخش اول مربوط به اثر میدان الکتریکی و بخش دوم مربوط به اثر میدان مغناطیسی است. اگر زاویه ϕ را به‌‌عنوان زاویه بین راستای حرکت ذره و میدان مغناطیسی در نظر بگیریم، اندازه نیروی لورنتس را بصورت زیر خواهیم داشت:

$$F= qE+qvB\sin\phi$$

یک مثال در این زمینه حل می‌کنیم تا با نحوه استفاده از قانون لورنتس بیشتر آشنا شوید:

مثال در مورد قانون لورنتس

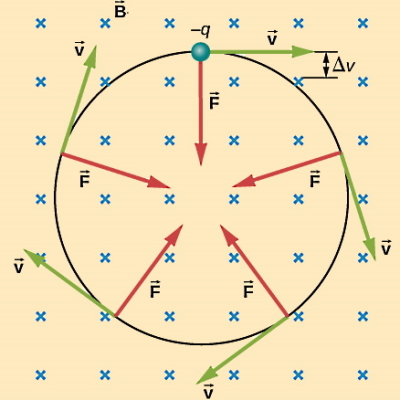
حرکت ذره بارداری با بار منفی را در حضور یک میدان مغناطیسی یکنواخت (عمود به سمت داخل صفحه) و نبود میدان الکتریکی در نظر بگیرید. اگر راستای حرکت ذره بر راستای میدان عمود باشد، مسیر حرکت ذره چگونه است؟

پاسخ

طبق صورت سوال، سرعت بر میدان عمود است و داریم E = 0 و B = مقداری ثابت. پس طبق رابطه بالا برای اندازه نیروی لورنتس خواهیم داشت:

$$F=qvB$$

چون در هر نقطه همواره جهت نیروی لورنتس بر میدان و سرعت عمود است، پس در هر نقطه جهت نیرو به سمت مرکز دایره‌ای فرضی خواهد بود. دقت کنید که تاثیر علامت بار را در منفی شدن جهت نیرو فراموش نکنید. در واقع نیروی لورنتس در این مساله با «نیروی مرکزگرا» (Centripetal Force) که برابر است با mv²/r معادل است. مسیر حرکت ذره به‌صورت یک دایره طبق شکل زیر است. شتاب‌دهنده‌‌‌های ذرات باردار مانند سیکلوترون‌‌ها بر همین اساس کار می‌کنند.

$$qvB=m\frac{v^2}{r}\Rightarrow r=\frac{mv}{qB}$$

اثر هال

یک کاربرد جالب قانون لورنتس، اثر هال (Hall Effect) است که طبق آن نیروی مغناطیسی وارد بر ذره باردار در حال حرکت می‌تواند علامت حامل‌های بار در یک رسانا را تعیین کند. می‌دانیم زمانی که جریان (j) در یک رسانا از سمت چپ به راست برقرار است، بدین معناست که حامل‌های بار مثبت در این رسانا از سمت چپ به راست در حال حرکتند یا حامل‌های بار منفی از سمت راست به چپ در حال حرکت‌اند. فرض کنید که این رسانا در یک میدان مغناطیسی (B) به گونه‌ای قرار داده شود که راستای جریان عبوری بر راستای میدان عمود باشد.

پس قبل از اعمال میدان مغناطیسی حامل‌های بار از سمت راست به چپ یا برعکس، در عرض رسانا در حال حرکت‌اند. اما با اعمال میدان، نیروی مغناطیسی ایجاد شده در راستای y باعث انحراف مسیر حرکت حامل‌ها و در نتیجه جمع شدن آنها در بالا یا پایین رسانا می‌شود. بنابراین نیروی مغناطیسی موجب افزایش اختلاف پتانسیل بین دو سر دیگر رسانا می‌شود و یک میدان الکتریکی به نام میدان هال (E_H) را ایجاد می‌کند. این میدان مجددا بر حرکت حامل‌ها اثر دارد و نیروی الکتریکی ناشی از آن همواره در خلاف جهت نیروی مغناطیسی است.

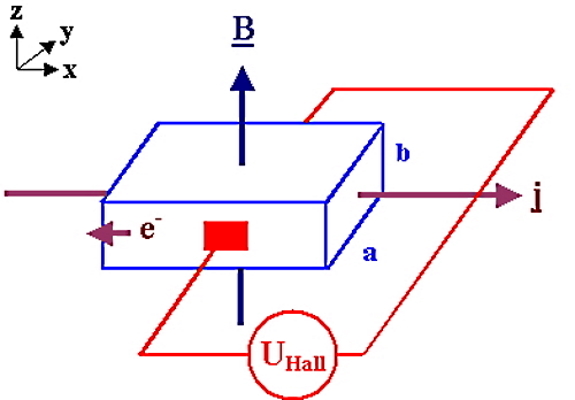
با مساوی قرار دادن این دو نیرو می‌توان مقدار اختلاف پتانسیلی که در راستای y ایجاد می‌شود، یعنی ولتاژ هال (U_H) را محاسبه کرد. در نهایت با ساده سازی، رابطه ضریب هال (R_H) به شکل زیر خواهد شد که در آن q معادل بار یک الکترون است و n چگالی حامل‌های بار است:

$$R_{H}= \frac{U_{H}a}{IB}$$

$$R_{H}= \frac{1}{nq}$$

در آزمایش برای تعیین ضریب هال با اندازه‌گیری ولتاژ دو سر رسانا و در اختیار داشتن مقدار جریان، میدان و اندازه عرض رسانا به آسانی می‌توانیم از رابطه اول ضریب هال را بدست آوریم و با قرار دادن آن در رابطه دوم، نوع حامل بار را تعیین کنیم. به کمک اثر هال است که می‌دانیم حامل‌های بار غالب در رسانایی مس (Copper) الکترون‌ها هستند، در حالی که در مورد رسانایی روی (Zinc) حامل‌‌‌های بار مثبت حامل‌های غالب هستند.

القای الکترومغناطیسی

رسانایی که به‌صورت الکتریکی باردار شده است را در نظر بگیرید. اگر این رسانا را در یک میدان مغناطیسی حرکت دهیم، چه اتفاقی رخ می‌دهد؟ به علت تغییرات شار مغناطیسی، یک جریان القایی یا اختلاف پتانسیل الکتریکی القایی در رسانا ایجاد می‌شود. چنین پدیده‌ای القای الکترومغناطیسی نام دارد. پیش از صحبت در مورد القای الکترومغناطیسی در قالب «قانون القای فارادی» (Faraday's Law of Induction)، بهتر است ابتدا با مفهوم شار آشنا شویم.

شار مغناطیسی

«شار» (Flux) یک مفهوم موثر در بررسی جهت و راستای عبور یک کمیت از سطح یا درون یک ماده یا فضاست. برای مثال می‌خواهیم شار عبوری آب باران از یک حلقه دایره‌ای شکل که در مسیر عبور آب قرار گرفته را بررسی کنیم. اگر مساحت سطح حلقه معادل A باشد، زمانی که حلقه بصورت عمود در مسیر عبور آب قرار بگیرد، بیشترین شار عبوری را دریافت کرده است. اما اگر راستای مسیر آب با سطح حلقه دارای زاویه کمتر از ۹۰ درجه باشد، شار عبوری نیز کمتر است. بنابراین زاویه مسیر آب با سطح حلقه کمیتی تعیین کننده در مقدار شار است.

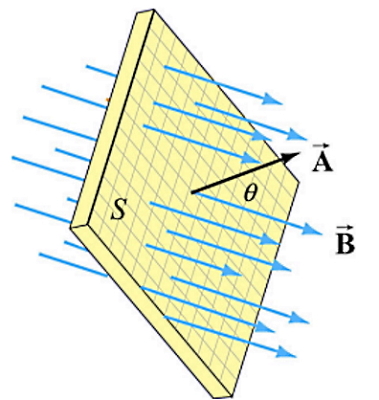
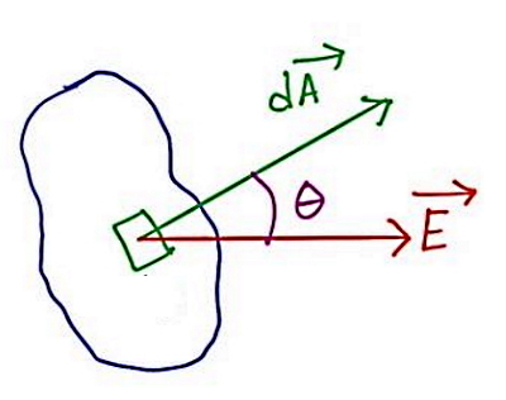
مرسوم است برای تعیین جهت‌گیری یک سطح از بردار عمود بر سطح A استفاده شود. در مبحث الکترومغناطیس لازم است بدانیم شار میدان الکتریکی روی یک سطح بسته می تواند اندازه‌ای از کل بار الکتریکی درون آن سطح را بدست دهد (قانون گاوس). اما شار میدان مغناطیسی برای چنین سطح بسته‌ای صفر است، زیرا مفهومی به نام بار مغناطیسی معادل با مفهوم بار الکتریکی وجود ندارد. حال اگر بخواهیم شار عبوری میدان مغناطیسی B را از سطح A بدست آوریم، اندازه این شار بصورت Φ_B = B.A خواهد بود.

علامت دات در این رابطه نشان‌دهنده ضرب داخلی بین دو کمیت برداری میدان و بردار عمود بر سطح است. اگر این ضرب داخلی را باز کنیم، رابطه بصورت BAcosθ خواهد شد که اثر زاویه θ بین بردار عمود بر سطح و راستای میدان در اینجا کاملا مشهود است. واحد شار مغناطیسی که آن را با Φ_B نشان می‌دهیم، وبر (Weber) است. یک وبر معادل یک تسلا بر متر مربع است.

قانون القای فارادی

قانون القای فارادی یا قانون القای الکترومغناطیسی قانون اصلی الکترومغناطیس محسوب می‌شود. این قانون کمک می‌کند تا برهم‌کنش میدان مغناطیسی با یک مدار الکتریکی و در نتیجه تولید «نیروی الکتروموتیو» (Electromotive Force) یا emf را پیش‌بینی کنیم. قانون القای فارادی دارای دو نتیجه مهم است:

• یک میدان مغناطیسی متغیر با زمان در یک مدار الکتریکی می‌تواند نیروی الکتروموتیو القا کند.
• اندازه این نیروی الکتروموتیو معادل نرخ تغییرات شار مغناطیسی با زمان است.

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

راه‌های مختلفی برای تغییر شار وجود دارد و نکته جالب در مورد قانون القای فارادی این است که مستقل از علت تغییر شار، همواره این قانون معتبر است. مطابق شکل زیر مقدار نیروی الکتروموتیو توسط قانون القای فارادی به‌صورت زیر خواهد بود:

$$ε =- N \frac{d\phi_B}{dt}$$

در این رابطه Φ_B شار عبوری بردار میدان مغناطیسی N ،B تعداد دورهای سیم و ε مقدار نیروی الکتروموتیو است. اگر بخواهیم در این رابطه دقیق‌تر شویم، می‌توانیم رابطه مربوط به شار مغناطیسی را باز کنیم و در نتیجه خواهیم داشت:

$$\epsilon=-N\frac{d}{dt}(BA~cos~\theta)=-N(\frac{dB}{dt})A~cos~\theta-NB(\frac{dA}{dt})cos~\theta+NBAsin~\theta(\frac{d\theta}{dt})$$

از رابطه بالا مشخص است که emf القایی را می‌توانیم با روش‌های مختلفی بدست آوریم:

• تغییر اندازه میدان مغناطیسی با زمان (جمله اول): در شکل با کمتر شدن تعداد خطوط میدان کاهش قدرت میدان نشان داده شده است.

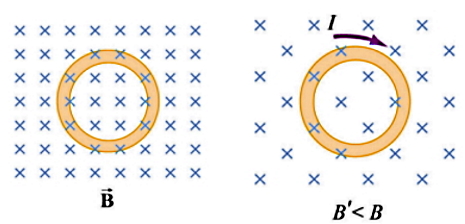
• تغییر اندازه مساحت A (جمله دوم)

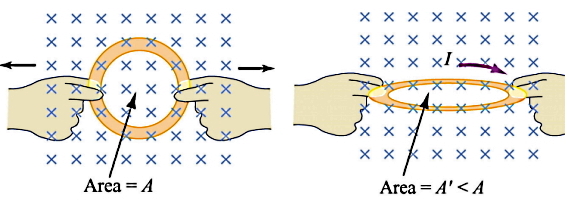
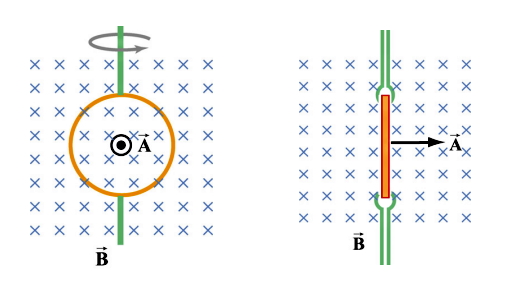
• تغییر زاویه بین میدان و بردار عمود بر سطح A (جمله سوم)

برای درک بهتر قانون القای فارادی، مثال‌های زیر را با هم حل می‌کنیم:

مثال ۱ در مورد قانون فارادی

یک حلقه دایره‌ای شکل با شعاع ‎0.1 m و 50 دور سیم را در نظر بگیرید. اگر این حلقه در میدانی قرار داده شود که به‌صورت یکنواخت از ‎0.5 T به ‎1 T طی بازه زمانی ‌‎2 s تغییر می‌کند، نیرو محرکه القایی در حلقه را با فرض θ=0 حساب کنید:

پاسخ

در این مثال تغییرات شار مغناطیسی از طریق تغییرات اندازه میدان اتفاق می‌افتد. بنابراین برای مقدار emf خواهیم داشت:

$$\epsilon=-N\frac{d(\phi_B)}{dt}=-N(\frac{dB}{dt})A~cos~\theta$$

$$\epsilon=-50(\frac{1-0.5}{2})\pi (0.1)^2= -0.39 V$$

مثال ۲ در مورد قانون فارادی

فرض کنید یک میله رسانا به طول L در حضور میدان مغناطیسی یکنواخت (عمود به سمت داخل صفحه) و میدان الکتریکی ثابت (جهتی از سمت بالا به پایین میله)، در حال عبور از فضایی است. برای emf القایی در اثر حرکت میله رابطه مناسب را پیدا کنید:

پاسخ

در داخل میله هر دو نوع حامل بار مثبت و منفی وجود دارد. نیروی مغناطیسی وارد شده به هر بار برابر F_B = qv×B خواهد بود. جهت نیرو برای هر بار مطابق شکل زیر است:

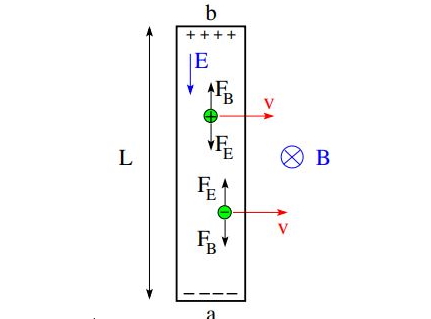
همچنین نیروی الکتریکی F_E = qE به علت حضور میدان E وجود دارد. علامت این نیرو هم با توجه علامت بارها مطابق شکل بالا خواهد شد. در حالت تعادل، از مساوی قرار دادن این نیروها اریم:

$$qE = qvB \Rightarrow E=vB$$

حالا اگر بخواهیم اختلاف پتانسیل بین دو سر میله رسانا را محاسبه کنیم، می‌نویسیم:

$$V_{ab} = V_b - V_a = EL \Rightarrow V_{ab} =vBL$$

این اختلاف پتانسیل، همان مقدار نیروی الکتروموتیو القایی حرکتی است.

قانون لنز

وجود علامت منفی در رابطه قبلی موضوع «قانون لنز» (Lenz's Law) است. این علامت نشان‌دهنده جهت نیروی الکتروموتیو نهایی و در نتیجه نشان‌دهنده جهت جریان القا شده است. طبق این قانون، جهت نیروی الکتروموتیو القایی به گونه‌ای است که تمایل دارد یک جریان مخالفت کننده تولید کند. بدین معنا که این جریان همواره با تغییرات شار مغناطیسی که آن را ایجاد کرده است، مخالفت می‌کند. بنابراین شار مغناطیسی که توسط جریان القایی تولید می شود همواره در جهتی است که از تغییرات شار کل در مدار، جلوگیری کند.

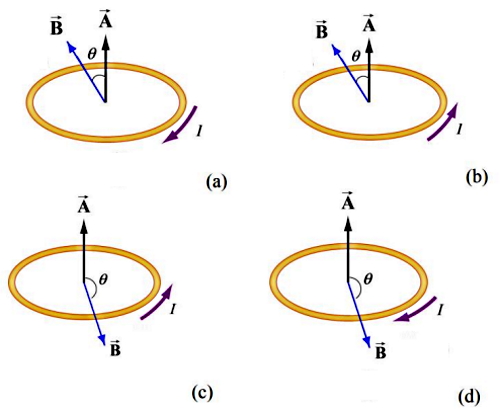
اگر بخواهیم نشان دهیم قانون لنز چگونه عمل می‌کند، یک حلقه سیم رسانا را در نظر بگیرید که در میدان مغناطیسی یکنواخت B قرار دارد. اگر جهت بردار عمود بر سطح A را مثبت در نظر بگیریم، برای عبارت dΦ_B/dt سه حالت خواهیم داشت: مثبت، منفی یا معادل صفر. حالا با استفاده از قانون دست راست و مطابق شکل زیر می‌توانیم جهت جریان القایی I را بدست آوریم.

انگشت شست خود را در جهت بردار A قرار داده و سایر انگشتان دست را در جهت حلقه بسته شده می‌چرخانیم. جهت جریان در راستای جهت سایر انگشتان دست (پادساعتگرد) است، اگر نیروی الکتروموتیو مثبت باشد و اگر نیروی الکتروموتیو منفی باشد، جهت جریان القایی در خلاف جهت راستای سایر انگشتان (ساعتگرد) است.

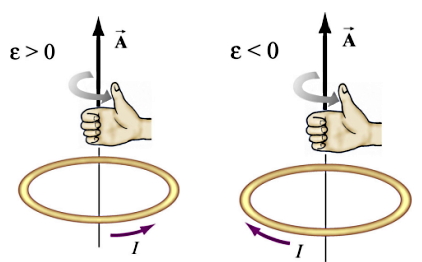
اگر بطور دقیق‌تر بخواهیم بررسی کنیم، در واقع چهار سناریو برای تغییرات شار مغناطیسی با زمان و در نتیجه استفاده از قانون لنز برای تعیین جهت جریان القایی وجود دارد. فرض می‌کنیم برای حالت‌های مختلف شرایط زیر برقرار است:

• حالت اول

$$(a)=\begin{cases}\frac{dB}{dt} >0 \\ \frac{d\phi_B}{dt} >0 \\ \phi_B >0\end{cases}$$

• حالت دوم

$$(b)=\begin{cases}\frac{dB}{dt} <0 \\ \frac{d\phi_B}{dt} <0 \\ \phi_B >0\end{cases}$$

• حالت سوم

$$(c)=\begin{cases}\frac{dB}{dt} >0 \\ \frac{d\phi_B}{dt} <0 \\ \phi_B <0\end{cases}$$

• حالت چهارم

$$(d)=\begin{cases}\frac{dB}{dt} <0 \\ \frac{d\phi_B}{dt} >0 \\ \phi_B <0\end{cases}$$

در شکل و جدول زیر به‌طور خلاصه این چهار سناریو نمایش داده شده است. دقت شود در این شکل منظور از مثبت و منفی برای جریان، به ترتیب جهت‌‌های پادساعتگرد و ساعتگرد است.

برای نمونه مورد حالت (c) را می‌توانیم در شکل زیر ببینیم. یک آهنربای میله‌ای به حلقه سیم حامل جریان نزدیک می‌شود. جهت میدان مغناطیسی آهنربا به سمت پایین و بردار عمود بر سطح حلقه سیم یعنی A به سمت بالا است. در نتیجه داریم: Φ_B = -AB<0. با حرکت دادن آهنربا به سمت داخل حلقه سیم، شدت میدان مفناطیسی با زمان افزایش می یابد. بنابراین dB/dt>0 و در نتیجه dΦ_B/dt = -A (dB/dt)< 0. منفی این رابطه در منفی رابطه قانون القای فارادی ضرب شده و در نهایت مقدار نیروی الکتروموتیو مثبت خواهد شد. طبق قانون دست راست در این حالت جریان القایی در جهت پادساعتگرد یا مثبت جریان خواهد یافت.

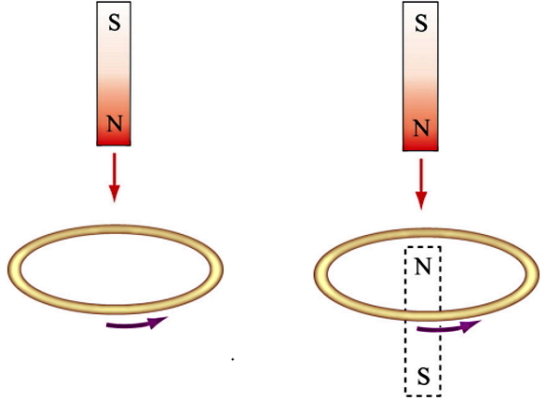
حالا خود این جریان، ایجاد یک شار مغناطیسی القایی در جهت مثبت می‌کند تا با تغییرات بیشتر شار اولیه مخالفت شود. پس با نزدیک‌تر کردن بیشتر آهنربا به حلقه سیم، آهنربا نیروی دافعه ناشی از نیروی الکتروموتیو را احساس می‌کند و این هدف اصلی قانون لنز است.

معادلات ماکسول

تا اینجا یاد گرفتیم که الکترومغناطیس چیست. اگر بخواهیم آنچه گفته شد را بطور خلاصه بیان کنیم، می‌توانیم چهار معادله ماکسول را مطالعه کنیم. در واقع این معادلات روند ایجاد و نحوه رفتار میدان‌های الکترومغناطیسی را بیان می‌کنند و به نوعی قوانین اصلی الکترومغناطیس محسوب می‌شوند. همچنین این معادلات تمام قوانین خودسازگار و مهم فیزیک مانند قوانین پایه اپتیک، پایستگی انرژی، پایستگی بار، پایستگی تکانه و پایستگی تکانه زاویه ای را پوشش می‌دهند:

• هر ذره باردار الکتریکی می‌تواند یک میدان الکتریکی ایجاد کند (قانون گاوس).
• در طبیعت ذره باردار مغناطیسی وجود ندارد و بنابراین ایجاد میدان مغناطیسی شبیه آنچه در مورد میدان الکتریکی گفتیم، نخواهد بود. این اصل را قانون گاوس برای مغناطیس می‌نامند.
• یک میدان مغناطیسی متغیر با زمان یک میدان الکتریکی ایجاد می کند (قانون القای فارادی).
• یک بار الکتریکی در حال حرکت یا در حال چرخش می‌تواند یک میدان مغناطیسی ایجاد کند (قانون آمپر). همچنین یک میدان الکتریکی متغیر با زمان نیز می تواند یک میدان مغناطیسی تولید کند. ترکیب این دو پدیده را «قانون آمپر-ماکسول» می نامند.

امواج الکترومغناطیسی

هر دو عنصر الکتریسیته و مغناطیس در عین حال که می‌توانند استاتیک باشند (مانند آنچه که یک بالن را روی دیوار یا یک آهنربا را روی یک فلز ثابت نگه می‌دارد)، می‌توانند متغیر با زمان بوده و با هم حرکت کنند. در این حالت است که امواج الکترومغناطیسی (Electromagnetic Waves) ایجاد شده‌اند. این امواج شامل میدان‌های الکتریکی و مغناطیسی بهم جفت شده و در حال نوسان‌اند که راستای این دو میدان بر یکدیگر و بر راستای حرکت موج عمود است. این نوسانات بسته‌های کوانتومی به نام «فوتون» (Photon) را تشکیل می‌دهند که کوانتوم امواج الکترومغناطیسی محسوب می‌شود. بر‌خلاف امواج صوتی که برای عبور از فضا به مولکول‌های ماده نیاز دارند، این امواج توانایی عبور از هر دو محیط خلا و ماده را دارند. بنابراین کاربرد این امواج بسیار گسترده‌تر است.

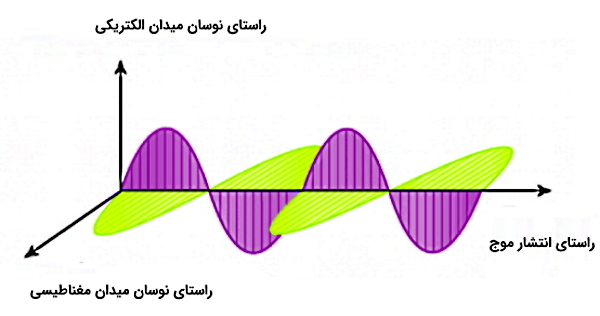
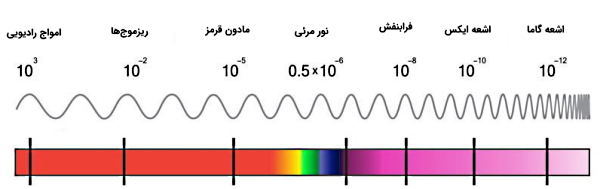
طیف الکترومغناطیسی شامل محدوده‌ای از تمام طول‌‌موج‌ها و فرکانس‌های ممکن برای امواج الکترومغناطیسی است. این طیف شامل امواج رادیویی و تلویزیونی، میکروموج‌ها یا ریزموج‌‌‌‌‌ها (Microwave)، امواج مادون قرمز (Infrared)، نور مرئی (Visible Light)، اشعه فرابنفش (Ultraviolet)، اشعه ایکس (X-ray) و اشعه گاما (Gamma-ray) می‌شود. تمام این امواج با سرعت یکسانی (سرعت نور) حرکت می‌کنند و تنها تفاوت‌ بین آنها فرکانس یا طول‌‌موجی است که در آن میدان‌های الکتریکی و مغناطیسی نوسان می‌کنند. ارتباط بین طول موج λ، فرکانس ν و سرعت نور c برای یک موج الکترومغناطیس توسط رابطه زیر بیان می‌شود.

$$c = \nu\lambda$$

در رابطه بالا با توجه به ثابت بودن سرعت نور، کوتاه‌ترین طول‌موج‌‌ها دارای بیشترین انرژی هستند. این مساله برای طیف الکترومغناطیسی در شکل زیر نشان داده شده است.

کاربرد‌های الکترومغناطیس

کاربردهای الکترومغناطیس در زندگی امروز بسیار گسترده است، از امواج رادیویی و تلویزیونی گرفته تا ساخت قطارهای با سرعت بالا و سیستم‌های ارتباطی انتقال داده. در تمام این موارد از اصول الکترومغناطیس استفاده می‌شود. در ادامه به توضیح دو مورد از پرکاربردترین ابزارهای ساخته شده بر اساس الکترومغناطیس می‌پردازیم.

فیلم آموزش فیزیک – پایه دوازدهم در فرادرس

کلیک کنید

الکترومگنت

یکی از ابتدایی‌ترین و مهم‌ترین کاربردهای الکترومغناطیس «الکترومگنت» (Electromagnet) است. در بخش میدان مغناطیسی گفتیم که میدان ناشی از مواد مغناطیسی چندان قوی نیست و لازم است برای تقویت‌ آن از الکتریسیته استفاده کنیم. برای مثال می‌توانیم از سیم‌پیچ‌های حامل جریانی که داخل آنها یک ماده مغناطیسی نرم مانند آهن به‌عنوان هسته قرار دارد، استفاده کنیم. چنین ابزاری الکترومگنت نام دارد و یکی از ساده‌ترین مثال‌های ترکیب الکتریسیته و مغناطیس یا الکترومغناطیس محسوب می‌شود.

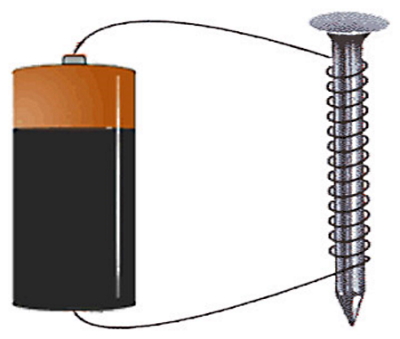
تفاوت الکترومگنت با یک آهنربای یخچالی معمولی این است که آهنربای یخچالی یک آهنربای دائمی ساخته شده از یک ماده مغناطیسی است که همیشه میدان مغناطیسی ضعیفی تولید می‌کند. اما الکترومگنت زمانی میدان مغناطیسی تولید می‌کند که نیاز است. همچنین میزان قدرت و قطب‌های یک آهنربای یخچالی ثابت است، ولی برای الکترومگنت می‌توان قدرت میدان و قطب‌ها را با تغییر تعداد دورهای سیم در سیم‌پیچ و تغییر جهت جریان آن تغییر داد. یکی از مرسوم‌ترین کاربردهای الکترومگنت‌ها در تصویربرداری از اجزای داخلی بدن انسان توسط سیستم «تصویربرداری رزونانس مغناطیسی» (Magnetic Resonance Imaging) یا (MRI) است.

بلندگوهای مغناطیسی

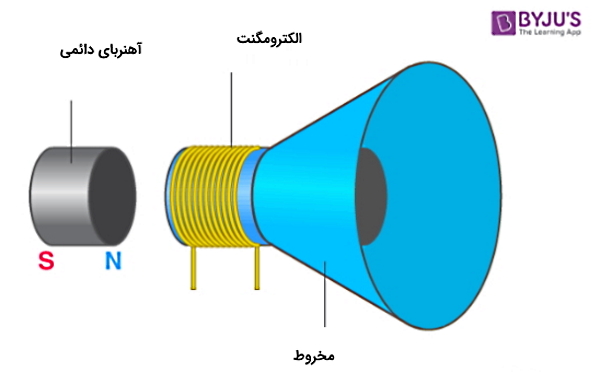
بلندگوی مغناطیسی دائمی که معمولا در تلویزیون‌ها و رادیوها استفاده می‌شود، یک نمونه ابزار کاملا الکترومغناطیسی است. در شکل زیر می‌توانیم ببینیم این ابزار چگونه براساس الکترومغناطیس کار می‌کند. بلندگو وسیله‌ای برای تبدیل امواج الکتریکی به صدای قابل شنیدن است. یک سیم‌پیچ فلزی که به یک آهنربای دائمی متصل است را در نظر بگیرید. زمانی که جریان از داخل سیم‌پیچ عبور می‌کند، یک میدان مغناطیسی تولید می‌شود. میدان مغناطیسی جدید توسط میدان اولیه آهنربای دائمی دفع می‌شود و در نتیجه نوساناتی ایجاد خواهد شد. این نوسانات به‌وسیله یک ساختار مخروطی شکل تقویت شده و صدا ایجاد می‌شود.

دیدگاه کوانتومی

تمام کمیت‌هایی که تا اینجا بیان شد، مانند بار الکتریکی، گشتاور مغناطیسی و میدان الکترومغناطیسی، هر کدام بصورت بسته‌های کوانتومی مجزا و تقسیم‌ناپذیر تعریف شده‌‌‌اند. برای مثال می‌دانیم بار الکتریکی یک کمیت کوانتیده است که کوانتوم آن بصورت بار یک ذره بنیادی مانند الکترون در نظر گرفته می‌شود. همچنین کوانتوم گشتاور مغناطیسی ذاتی نیز گشتاور ذره بنیادی بارداری مانند الکترون در نظر گرفته می‌شود که «اسپین» (Spin) نام دارد. کوانتوم میدان الکترومغناطیسی نیز همانطور که اشاره شد، فوتون است. اگر بخواهیم توصیف دقیق‌تری از الکترومغناطیس ارائه دهیم، باید شکل کوانتومی تمامی قوانین فیزیکی بیان شده تا به اینجا را بررسی کنیم.

در واقع معادلات ماکسول اگرچه توصیف خوبی از الکترومغناطیس بیان کردند، اما در مقیاس زیراتمی دید خاصی ارائه نمی‌دهند. دانشمندان مختلفی مانند آلبرت انیشتین (Albert Einstein)، ورنر هایزنبرگ (Werner Heisenberg) و پاول دیراک (Paul Dirac) در بناگذاری ماهیت کوانتومی الکترومغناطیس نقش داشته‌اند. در حال حاضر از ترکیب قوانین کوانتومی الکترومغناطیس و نظریه نسبیت خاص شاخه‌ای به نام «الکترودینامیک کوانتومی» (Quantum Electrodynamic) یا به اختصار QED حاصل شده است که دقیق‌ترین نظریه الکترومغناطیس را ارائه می‌دهد. با این وجود همچنان مسائل حل نشده‌ای مانند وجود بار مغناطیسی و نظریه یکپارچه‌سازی الکترومغناطیس با برهم‌کنش هسته‌ای قوی و گرانش در این حوزه وجود دارند.

جمع‌بندی

بطور کلی گفتیم که الکترومغناطیس شاخه‌ای از علم فیزیک است که به بررسی آثار ناشی از برهم‌کنش بارهای الکتریکی، گشتاورهای مغناطیسی و میدان‌‌‌‌های الکترومغناطیسی با یکدیگر می‌پردازد. جزئیات این برهم‌کنش‌ها و فرمول‌بندی آنها را به‌عنوان قوانین الکترومغناطیس به‌طور خلاصه در قالب چهار معادله ماکسول شامل قانون گاوس، قانون القای فارادی و قانون آمپر مطالعه کردیم.

همچنین دیدیم که یک میدان الکترومغناطیسی می‌تواند به شکل استاتیکی یا متغیر با زمان باشد و یا به‌صورت امواج منتشر شود. امواج الکترومغناطیسی عموما به اسم نور شناخته می‌شوند و بسته به طول‌موج‌شان، دارای کاربردهای مختلفی در زندگی روزمره هستند. برای بدست آوردن دید دقیق‌تری نسبت به الکترومغناطیس، لازم است از ترکیب الکترومغناطیس، قوانین کوانتوم و نسبیت استفاده کنیم.