گشتاور مغناطیسی — به زبان ساده

گشتاور کمیتی است که در حرکت‌های چرخشی و دورانی حول یک محور ثابت قابل محاسبه است. در این مطلب در مورد گشتاور مغناطیسی صحبت می‌کنیم و نحوه محاسبه آن را بررسی می‌کنیم و با حل چند مثال سعی می‌کنیم تا موضوع به خوبی در ذهن خواننده ملموس و قابل فهم شود.

گشتاور چیست؟

گشتاور مقدار نیرویی است که می‌تواند باعث چرخش یک جسم حول محور ثابت شود. همان طور که نیرو باعث سرعت گرفتن یک جسم در سینماتیک خطی می‌شود گشتاور نیز همان چیزی است که باعث می‌شود جسم شتاب زاویه‌ای پیدا کند. گشتاور یک بردار است و جهت بردار گشتاور بستگی به جهت نیرو در محور دارد.

هر زمان دربی را باز می‌کنید نیروی گشتاور وارد عمل می‌شود. احتمالاً شما نیز این تجربه را داشته‌اید هنگامی که دربی را باز می‌کنید و از فاصله دورتری از لولاهای درب به آن فشار می‌آورید برای باز کردن درب به نیروی کمتری نیاز دارید. اما میزان نیرویی که برای باز کردن همان درب لازم است در حالی که نزدیک به لولاها نیرو وارد می‌کنید به میزان قابل توجهی افزایش پیدا می‌کند. اگرچه کار انجام شده در هر دو حالت یکسان است زیرا نیروی بیشتری در فاصله کمتری اعمال شده اما ما معمولاً ترجیح می‌دهیم نیروی کمتری وارد کنیم، از این رو محل معمول دستگیره درب در بیشترین فاصله از لولا قرار دارد.

گشتاور می‌تواند استاتیک یا پویا باشد. گشتاوری استاتیک است که شتاب زاویه‌ای تولید نمی‌کند. شخصی که درب بسته را فشار می‌دهد و آن را باز می‌کند گشتاور ایستایی را به درب وارد می‌کند زیرا با وجود نیرویی که وارد می‌شود درب دور لولاهای خود نمی‌چرخد. کسی که با سرعت ثابت پدال دوچرخه را رکاب می‌زند نیز گشتاور ایستا اعمال می‌کند زیرا دوچرخه شتاب نمی‌گیرد.

محور محرک یک اتومبیل مسابقه که از خط شروع شتاب می‌گیرد گشتاور دینامیک یا پویا ایجاد می‌کند زیرا با توجه به شتاب گرفتن ماشین در مسیر در چرخ‌ها شتاب زاویه‌ای ایجاد می‌شود.

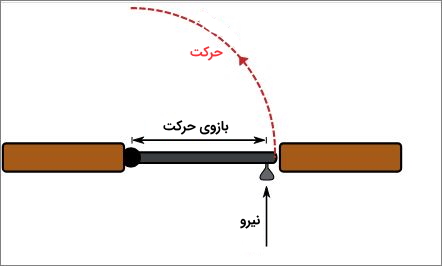
اصطلاحاتی که هنگام توصیف گشتاور استفاده می‌شود می‌توانند گیج کننده باشند. بعضی اوقات در برخی کتاب‌ها از اصطلاح ممان یا ممان نیرو به جای اصطلاح گشتاور استفاده می‌شود. همچنین به شعاعی که نیرو در آن اعمال می‌شود نیز بازوی ممان می‌گوییم که در تصویر (1) نمایش داده شده است. اگر می‌خواهید بیشتر در مورد گشتاور بخوانید این مطلب را مطالعه کنید.

تعریف گشتاور دوقطبی مغناطیسی

همان گونه که در مطلب نیروی مغناطیسی سیم حامل جریان بیان کردیم یک میدان مغناطیسی به یک سیم مستقیم حامل جریان نیرو وارد می‌کند و این نیرو سبب ایجاد یک گشتاور بر سیم پیچ حامل جریان می‌شود که به این کمیت گشتاور مغناطیسی می‌گوییم. گشتاور سبب می‌شود که جسم حول یک محور ثابت بچرخد.

روش محاسبه گشتاور مغناطیسی

یک میدان مغناطیسی روی یک سیم مستقیم حامل جریان نیرو اعمال می‌کند. همچنین این میدان بر روی یک حلقه سیم حامل جریان گشتاور وارد می‌کند. همان طور که در قسمت قبل گفتیم گشتاور پویا باعث چرخش یک شی در اطراف یک محور ثابت می‌شود.

بردار جریان هر حلقه جریان در راستای جریان است. جهت بردار نرمال این حلقه را به راحتی با قانون دست راست می‌توان به دست آورد. اگر چهار انگشت دست راست را در جهت چرخش جریان قرار دهید جهت انگشت شست جهت بردار نرمال عمود به سطح را نشان می‌دهد.

جهت گشتاوری که میدان مغناطیسی در یک حلقه سیم حامل جریان ایجاد می‌کند نیز در جهت بردار نرمال عمود بر صفحه است. در حقیقت این میدان مغناطیسی گشتاوری را اعمال می‌کند که تلاش می‌کند تا بردار نُرمال صفحه را با میدان مغناطیسی همراستا کند.

بدین ترتیب می‌توان گفت اندازه گشتاور یک حلقه جریان برابر با حاصلضرب تعداد دورهای سیم حامل جریان، جریان، مساحت حلقه، اندازه میدان مغناطیسی و سینوس زاویه بین جهت بردار نرمال صفحه و میدان مغناطیسی است و داریم:

$$\tau=N\times I\times B\times A\times \sin(\theta)$$

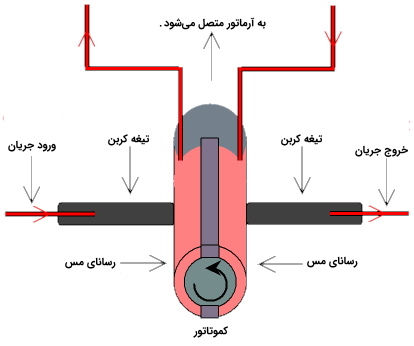
حلقه‌ای که حامل جریان مستقیم است در یک میدان مغناطیسی ثابت نمی‌چرخد و تنها حرکت رفت و برگشتی دارد. موتورهای DC برای چرخش کامل به اطراف باید از کموتاتور استفاده کنند. یک کموتاتور از دو قطعه نیم استوانه‌ای از جنس مس تشکیل شده‌ است و جهت جریان را معکوس می‌کند.

ایجاد یک میدان مغناطیسی با عبور جریان از طریق سیم نشان‌دهنده رابطه نزدیک بین الکتریسیته و مغناطیس است. قانون آمپر این امکان را فراهم می‌کند تا بتوان قدرت میدان مغناطیسی ایجاد شده را حول یک سیم حامل جریان محاسبه کرد و داریم:

$$B=\frac{\mu I}{2\pi R}$$

همان طور که می‌دانید $$\mu$$ ضریب تراوایی مغناطیسی خلاء و برابر با $$\mu=4\pi\times 10^{-7} \frac{Tm}{A}=1.257 \times 10^{-6} \frac{Tm}{A}$$ است. همچنین قدرت یک میدان مغناطیسی در مرکز سیم پیچ حامل جریان نیز برابر است با:

$$B=\frac{N \mu I}{2 R}$$

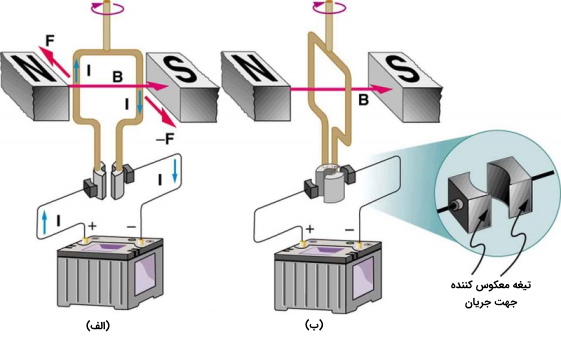
بنابراین امکان اعمال نیرو بر یک سیم از طریق میدان مغناطیسی امکان پذیر است. این موضوع در حالتی که بخواهیم یک حرکت دایره‌ای ایجاد کنیم مهم است چیزی که در موتورها یا چرخ‌ها اتفاق می‌افتد. با توجه به آنچه گفته شد برای ایجاد حرکت دورانی با استفاده از میدان مغناطیسی به یک سیملوله یا سیم پیچ نیاز داریم.

گشتاور مغناطیسی نیروی وارد بر حلقه جریان

موتورها متداول‌ترین دستگاه‌هایی هستند که در آن‌ها نیروی مغناطیسی بر روی سیم حامل جریان اعمال می‌شود. این دستگا‌ه‌ها دارای حلقه‌های سیم در یک میدان مغناطیسی هستند. وقتی جریان از حلقه‌ها عبور می‌کند میدان مغناطیسی بر روی حلقه‌ها گشتاور اعمال می‌کند که باعث چرخش میله داخل موتور می‌شود.

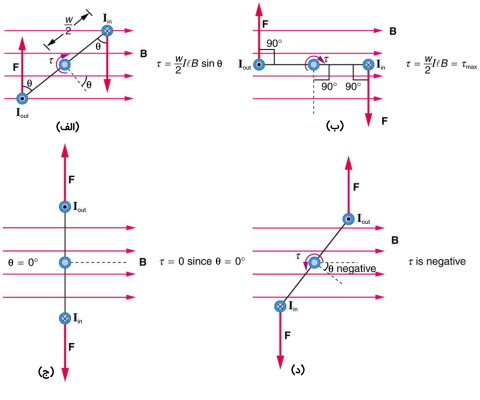
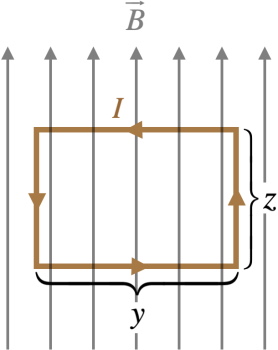
در این فرآیند و در موتور انرژی الکتریکی به کار مکانیکی تبدیل می‌شود. می‌خواهیم نیروی وارد شده بر هر قطعه از حلقه را در شکل (3) بررسی کنیم تا گشتاورهای تولید شده در محور میله عمودی را پیدا کنیم.

فرض می‌کنیم در حلقه مستطیل شکل میدان مغناطیسی یکنواخت برقرار باشد. این حلقه مستطیل شکل دارای عرض w و ارتفاع l است.

همان طور که می‌دانید نیروهای موجود در قسمت‌های بالا و پایین عمود و موازی با محور میله بوده و هیچ گشتاوری ایجاد نمی کنند. این دو نیرو از نظر جهت و اندازه نیز برابر و خلاف جهت یکدیگر هستند و نیروی خالصی نیز ایجاد نمی‌کنند.

تصویر (4) نماهای مختلفی از حلقه را از بالا نشان می‌دهد. گشتاور به صورت $$\tau=rf\sin(\theta)$$ تعریف می‌شود که F نیرو، r فاصله محوری است که نیرو اعمال می‌شود و $$\theta$$ زاویه بین r و F است. همان طور که در تصویر (الف) شکل بالا می‌بینید قانون دست راست سبب می‌شود تا جهت نیروها هم اندازه و خلاف جهت یکدیگر باشد و اثر یکدیگر را حذف کنند و بنابراین نیروی خالص صفر می‌شود.

با این حال هر نیرو گشتاوری در جهت عقربه‌های ساعت تولید می‌کند. از آنجا که $$r=\frac{w}{2}$$ است گشتاور در هر بخش عمودی برابر با $$\frac{w}{2}F \sin(\theta)$$ می‌شود و مجموع این دو گشتاور کل را می‌دهد.

$$\tau =\frac{w}{2}F\sin\theta +\frac{w}{2}F\sin\theta =wF\sin\theta$$

حال با توجه به اینکه طول $$l$$ عمود بر میدان B است، نیروی هر قسمت برابر با $$F=lIB$$ می‌شود. با وارد کردن مقدار نیرو در رابطه گشتاور داریم:

$$\tau=wIlB\sin\theta$$

اگر حلقه دارای $$N$$ دور باشد و با استفاده از رابطه مربوط به مساحت مستطیل که برابر با طول در عرض است می‌توان رابطه نهایی گشتاور را به صورت زیر نوشت و داریم:

$$\tau=NIAB\sin\theta$$

رابطه به دست آمده در بالا گشتاور یک حلقه حامل جریان در یک میدان مغناطیسی یکنواخت است. این حلقه دارای N دور، جریان I، سطح مقطع A و میدان مغناطیسی B است و این معادله می‌تواند برای یک حلقه از هر شکل برقرار باشد.

مثال: ماکزیمم گشتاور یک حلقه مربعی با طول 10 سانتی‌متر که حامل جریان 15 آمپری است و در یک میدان 2 تسلا قرار دارد در حالی که تعداد حلقه‌های آن 100 دور است را به دست آورید.

پاسخ: همان طور که گفتیم رابطه گشتاور برای یک حلقه برابر است با:

$$\tau =NIAB\sin\theta$$

ماکزیمم گشتاور زمانی است که $$\sin\theta$$ برابر با 1 و یا $$\theta=90$$ باشد و داریم:

$$\tau_{max}=NIAB$$

بدین ترتیب با قرار دادن مقادیر مربوط به جریان، سطح مقطع و تعداد دورهای حلقه جریان، گشتاور ماکزیمم برابر است با:

$$\begin{array}{lll}\tau_{\text{max}}& =& \left(100\right)\left(15.0 \text{ A}\right)\left(0.100\text{ m}^{2}\right)\left(2.00\text{ T}\right)\\ & =& 30.0 \text{ N}\cdot \text{m}\end{array}\\$$

این مقدار برای گشتاور به اندازه‌ای است که بتوان از آن در یک موتور استفاده کرد. گشتاور به دست آمده در مثال قبلی حداکثر است. با چرخش سیم پیچ گشتاور در $$\theta=0$$ به صفر می‌رسد. در ادامه پس از چرخش سیم پیچ از $$\theta=0$$ جهت گشتاور عکس می‌شود و این بدان معنی است که در صورتی که روی سیم پیچ کار انجام نشود سیم‌ پیچ حول نقطه $$\theta=0$$ حرکت رفت و برگشتی و نوسانی انجام می‌دهد.

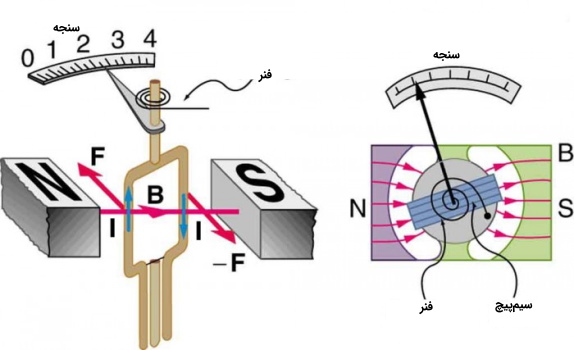
کنتورها ابزاری که برای مثال برای اندازه‌گیری سوخت اتومبیل بر روی ماشین قرار دارند، یکی دیگر از کاربردهای معمول گشتاور مغناطیسی در یک حلقه حامل جریان هستند. شکل زیر نشان می‌دهد که کنتورها یا سنجه‌ها از نظر ساختاری بسیار شبیه به موتور هستند. سنجه شکل زیر دارای ساختاری نعلی شکل شبیه به یک مگنت است که تاثیر $$\theta$$ را در محاسبات حداقل می‌کند، این ویژگی سبب می‌شود تا میدان در بازه بزرگی از حرکت تقریباً بر حلقه عمود باشد.

بنابراین گشتاور متناسب با $$I$$ است و به $$\theta$$ وابسته نیست. یک فنر که از قانون هوک پیروی می‌کند یک گشتاور در جهت مخالف ایجاد می‌کند که گشتاور تولید شده در جریان را متعادل کند. این ویژگی سبب می‌شود که انحراف تیغه سنجه با $$I$$ متناسب باشد، اگر تناسب دقیق حاصل نشود باید دستگاه اندازه‌گیری را کالیبره کرد. برای تولید گالوانومتر برای استفاده در ولت ‌مترها و آمپر مترهای آنالوگ که مقاومت کمی دارند و می‌توانند جریان‌های کوچک را اندازه‌گیری کنند از یک حلقه با سطح مقطع بزرگ A، میدان مغناطیسی بالای B و سیم پیچ‌هایی با مقاومت کم استفاده می‌کنیم.

مثال‌های گشتاور مغناطیسی

مثال 1: الف) اگر آهنرباهای دائمی یک موتور $$5\%$$ قدرت خود را از دست دهند، گشتاور موتور چند درصد کاهش می‌یابد؟ ب) چه قدر جریان نیاز است تا گشتاور مجدداً به مقدار اولیه خود بازگردد؟

پاسخ: الف) اگر میدان مغناطیسی $$5\%$$ کاهش یابد گشتاور نیز به همان اندازه کاهش می‌یابد زیرا میدان و گشتاور با یکدیگر رابطه مستقیم دارند. ب) با توجه به رابطه مستقیم جریان با گشتاور مغناطیسی برای اینکه گشتاور به مقدار اولیه خود بازگردد باید مقدار جریان را $$5\%$$ افزایش داد.

مثال 2: جریان عبوری از یک حلقه مورد نیاز برای ایجاد گشتاور $$9\ N.m$$ را پیدا کنید. در نظر بگیرید که این حلقه دارای 50 دور است که قاعده آن $$15$$ سانتی متر است و در یک میدان مغناطیسی یکنواخت $$0.8\ T$$ قرار دارد.

پاسخ: با توجه به رابطه گشتاور مغناطیسی داریم:

$$\tau =NIAB\sin\theta$$

با قرار دادن مقادیر داده شده در مسئله داریم:

$$\tau =NIAB\sin\theta\rightarrow 9=50 \times (15\times 10^{-2})^{2}\times 0.8 \times I$$

و در نتیجه داریم:

$$I=10\ (A)$$

ممان دوقطبی مغناطیسی

همان طور که گفتیم گشتاور مغناطیسی برابر با $$\tau=NIAB$$ است. در منابع مختلف حاصلضرب $$NIA$$ را با $$\mu$$ نمایش می‌دهند که در نهایت گشتاور را به صورت ساده شده $$\tau=\mu B$$ می‌نویسند. همچنین آموختیم میدان مغناطیسی و گشتاور هر دو کمیتی برداری هستند و گشتاور ایجاد شده در یک حلقه به نوع قرار گرفتن حلقه در میدان بستگی دارد. می‌توانیم نوع قرار گرفتن حلقه در یک میدان مغناطیسی را با $$\mu$$ نمایش دهیم که به آن ممان دوقطبی مغناطیسی نیز می‌گوییم. در حقیقت ممان دوقطبی مغناطیسی برابر است با:

$$\mu=NIA$$

که A بردار سطح است و جهتی در راستای عمود بر حلقه دارد که جهت این بردار عمود را همان طور که در بخش‌های قبل گفتیم از طریق قانون دست راست به دست می‌آوریم. به این صورت که چهار انگشت دست راست را در جهت جریان حرکت می‌دهیم و جهت انگشت شست نمایش دهنده بردار نُرمال عمود بر صفحه است. به عنوان مثال جهت بردار عمود بر صفحه شکل زیر برداری به سمت خارج صفحه است.

با این تعریف می‌توان رابطه گشتاور را به صورت زیر نوشت:

$$\tau_{magnetic}=\mu\times B$$

وقتی حلقه به دور محور افقی می‌چرخد زاویه بین گشتاور دو قطبی مغناطیسی و میدان تغییر می‌کند و بازوهای ممان نیروها با عامل $$\sin{\theta}$$ کاهش می‌یابند. هنگامی که حلقه به نقطه‌ای می‌رسد که میدان عمود بر صفحه باشد، ممان و میدان مغناطیسی موازی شده و گشتاور صفر می‌شود.

مثال: یک سیم با جریان 2 آمپر در یک رسانای دایروی با شعاع 12 سانتی متر در صفحه x-y قرار گرفته است. زمانی که از صفحه $$+z$$ به این حلقه نگاه می‌کنیم جهت جریان را ساعتگرد مشاهده می‌کنیم. اگر بردار میدان مغناطیسی به صورت زیر باشد، گشتاور و جهت بردار گشتاور را محاسبه کنید.

$$\overrightarrow B = B_o\left(\widehat i-3\widehat j + 2\widehat k\right)\rightarrow\;\;B_o=1.50T\nonumber$$

پاسخ: برای محاسبه گشتاور لازم است در ابتدا ممان مغناطیسی را حساب کنیم و داریم:

$$\overrightarrow \mu = IA\left(-\widehat k\right) = \left(2.00A\right)\pi\left(0.12m\right)^2\left(-\widehat k\right) = \left(-9.05\times 10^{-2} A\cdot m^2\right)\widehat k\nonumber$$

جهت بردار نرمال عمود بر صفحه نیز با استفاده از قانون دست راست به سمت داخل صفحه به دست می‌آید. با این نتیجه می‌توان بردار گشتاور را با استفاده از قوانین ضرب خارجی بردارها محاسبه کرد و داریم:

$$\overrightarrow \tau = \overrightarrow \mu \times \overrightarrow B = \left[\left(-9.05\times 10^{-2} A\cdot m^2\right)\widehat k\right]\times\left[\left(1.50T\right)\left(\widehat i-3\widehat j + 2\widehat k\right)\right] = -\left(0.136\;N\cdot m\right)\left(3\widehat i + \widehat j\right)\nonumber$$

گشتاور مغناطیسی الکترون

همان طور که گفتیم گشتاور مغناطیسی یک جسم برابر با حاصلضرب خارجی ممان دوقطبی مغناطیسی جسم در میدان مغناطیسی است. بدین ترتیب برای محاسبه گشتاور مغناطیسی یک الکترون باید ممان دوقطبی آن را بدانیم و از حاصلضرب ممان دوقطبی در میدان مغناطیسی می‌توان گشتاور مغناطیسی را محاسبه کرد.

الکترون‌ها و بسیاری از ذرات بنیادی دارای گشتاورهای مغناطیسی ذاتی هستند که توضیح آن‌ها نیاز به توضیح ساز و کار کوانتومی دارد و مربوط به حرکت زاویه‌ای ذاتی ذرات است. در حقیقت گشتاور مغناطیسی ذاتی این ذرات باعث ایجاد اثرات ماکروسکوپی مغناطیسی و سایر پدیده‌ها مانند تشدید پارامغناطیس الکترون‌ها می‌شود. بدین ترتیب می‌توان گشتاور مغناطیسی ذاتی یک الکترون را به صورت زیر به دست آورد:

$$m_{S}=-\frac{g_{S}\mu_{B}S}{\hbar}$$

در رابطه بالا $$\mu_B$$ یک ثابت در فیزیک اتمی است و برای تعریف ممان مغناطیسی الکترون استفاده می‌شود، S اسپین الکترون و $$g_S$$ یک کمیت ثابت هستند. مقدار فاکتور $$g_S$$ براساس نظریه دیراک برابر 2 است اما به دلیل اثرات الکترودینامیکی کوانتومی در واقعیت کمی بزرگتر و برابر با $$2.00231930436$$ است. انحراف $$g_S$$ از 2 به عنوان ناهنجاری ممان دوقطبی مغناطیسی شناخته می‌شود.

توجه به این نکته مهم است که m یک ثابت منفی است که در اسپین ضرب می‌شود، بنابراین گشتاور مغناطیسی الکترون موازی جهت چرخش الکترون نیست. این موضوع را می‌توان با تصویر کلاسیک زیر نیز درک کرد:

اگر تصور کنیم حرکت زاویه‌ای اسپین الکترون در اثر چرخش الکترون حول برخی از محورها ایجاد می‌شود جریان الکتریکی که این چرخش ایجاد می‌کند به دلیل بار منفی الکترون در جهت مخالف گردش خود الکترون است.

در نتیجه این حلقه‌های جریان یک گشتاور مغناطیسی تولید می‌کنند که خلاف جهت چرخش الکترون است. بدین ترتیب برای یک پوزیترون گشتاور مغناطیسی موازی جهت چرخش پوزیترون است.

با به دست آوردن ممان مغناطیسی یک الکترون محاسبه گشتاور مغناطیسی آن با توجه به میدانی که الکترون در آن قرار می‌گیرد به راحتی قابل محاسبه است.

گشتاور مغناطیسی یک حلقه بسته در میدان مغناطیسی ثابت

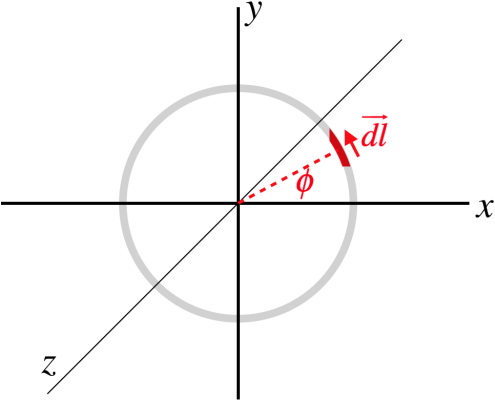
برای محاسبه گشتاور در یک حلقه بسته، حلقه‌ای را در صفحه x-y در نظر بگیرید که جهت بردار مغناطیسی در راستای $$+x$$ است. یک جزء کوچک حلقه را در نظر بگیرید که مانند شکل بالا با جهت مثبت محور x زاویه $$\phi$$ بسازد. جزء طول بی‌نهایت کوچک حلقه یعنی $$dl$$ برابر با $$Rd\phi$$ است. اگر جزء طول را در راستای x و y تجزیه کنیم داریم:

$$\overrightarrow {dl} = R\;d\phi\left(-\sin\phi\;\widehat i + \cos\phi\;\widehat j\right)$$

به این ترتیب هر آن چه لازم است برای محاسبه نیروی وارد بر حلقه حامل جریان داریم:

$$d\overrightarrow F = I \overrightarrow {dl} \times \overrightarrow B = I\left[R\;d\phi\left(-\sin\phi\;\widehat i + \cos\phi\;\widehat j\right)\right]\times\left[B \;\widehat i\right]$$

با استفاده از قوانین ضرب خارجی بردارها نیروی حاصل برابر است با:

$$d\overrightarrow F = IRB\cos\phi\;d\phi \left(-\widehat k\right)$$

برای محاسبه گشتاور برای یک جزء بی نهایت کوچک حلقه حامل جریان در میدان مغناطیسی داریم:

$$d\overrightarrow \tau = \overrightarrow r \times d\overrightarrow F = \left(R\cos\phi\;\widehat i + R\sin\phi\;\widehat j\right)\times \left(-IRB\cos\phi\;d\phi\;\widehat k\right) = -IR^2B\;d\phi\left[\cos^2\phi \left(-\widehat j\right) + \sin\phi \cos\phi \left(\widehat i\right)\right]$$

حال برای محاسبه گشتاور کل در محیط حلقه باید از جزء به دست آمده در بازه زاویه‌ای بین 0 تا $$2\pi$$ انتگرال بگیریم و در نتیجه داریم:

$$\overrightarrow \tau =-IR^2B\int\limits_0^{2\pi}d\phi\left[\cos^2\phi \left(-\widehat j\right) + \sin\phi \cos\phi \left(\widehat i\right)\right] = IR^2B\left[\pi \;\widehat j-0 \;\widehat i\right]=I\left(\pi R^2\right)B\;\widehat j$$

با توجه به اینکه گشتاور را برابر با $$\mu B$$ معرفی کردیم که در آن $$\mu=IA$$ است و استفاده از قانون دست راست که در نهایت گشتاور را به صورت $$\mu \times B$$ معرفی کردیم، جهت به دست آمده در رابطه بالا جهتی که پیش‌تر برای گشتاور معرفی کردیم را تایید می‌کند.

جمع‌بندی

در این مطلب در مورد گشتاور مغناطیسی صحبت کردیم. در ابتدا تعریفی برای گشتاور ارائه دادیم و سپس رابطه گشتاور مغناطیسی را به دست آوردیم. همچنین ممان دوقطبی مغناطیسی را محاسبه کردیم و گشتاور مغناطیسی یک الکترون و یک حلقه جریان را به دست آوردیم. برای درک بهتر موضوعات در هر بخش مثال‌هایی نیز حل کردیم.