انرژی فوتون — به زبان ساده

در مقاله «فوتون در فیزیک -- به زبان ساده» با فوتون یا همان کوانتوم نور آشنا شدید. همچنین در مقاله «طیف الکترومغناطیسی -- به زبان ساده» دیدیم که انرژی فوتون وابسته به این امواج، محدودهای به شکل زیر دارد:
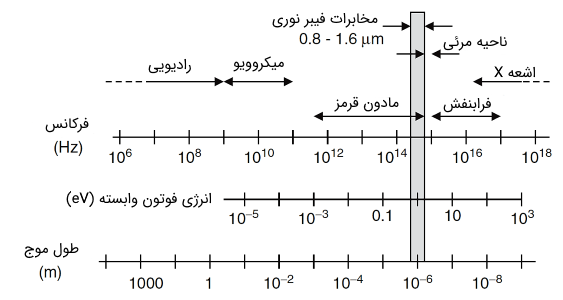
در این مقاله کوتاه قصد داریم تا با زبانی ساده به مقوله انرژی فوتون بپردازیم. با ما در ادامه این مطلب همراه باشید.
انرژی فوتون (Photon Energy)
انرژی فوتون، مقدار انرژی است که توسط یک تک فوتون حمل میشود. در مقاله «دوگانگی موج و ذره — به زبان ساده» دیدیم که نور ماهیتی دوگانه دارد. نور با استفاده از تعریف فوتون، ماهیتی ذرهای و با تعریف امواج الکترومغناطیسی، ماهیتی موجی دارد. این مطلب تنها برای نور یعنی ناحیه مرئی صادق نبوده و میتوان آن را به تمام طیف الکترومغناطیسی تعمیم داد.
در مقاله «معادله شرودینگر -- به زبان ساده» دیدیم که دوبروی به هر ذرهای که دارای تکانه باشد، موجی با طول موج λ به شکل زیر تخصیص داد. در رابطه زیر نیز عدد موج (بردار موج در ۳ بعد) است.
(1)
(2)
با این اوصاف، هر موج الکترومغناطیسی را میتوان یک فوتون نیز در نظر گرفت که به آن فوتون وابسته به امواج الکترومغناطیسی میگویند. مقدار انرژی فوتون به صورت زیر محاسبه میشود.
(3)
(4)
(5)
در رابطه فوق ثابت پلانک و فرکانس موج الکترومغناطیسی متناظر با فوتون است. در برخی منابع، فرکانس را با نماد (بخوانید نوو) نمایش میدهند. ملاحظه میکنید که انرژی فوتون با فرکانس رابطهای خطی داشته و با افزایش فرکانس مقدار انرژی آن نیز افزایش پیدا میکند. طبق رابطه فرکانس و طول موج، مقدار انرژی فوتون را میتوان به صورت زیر نیز نوشت:
(6)
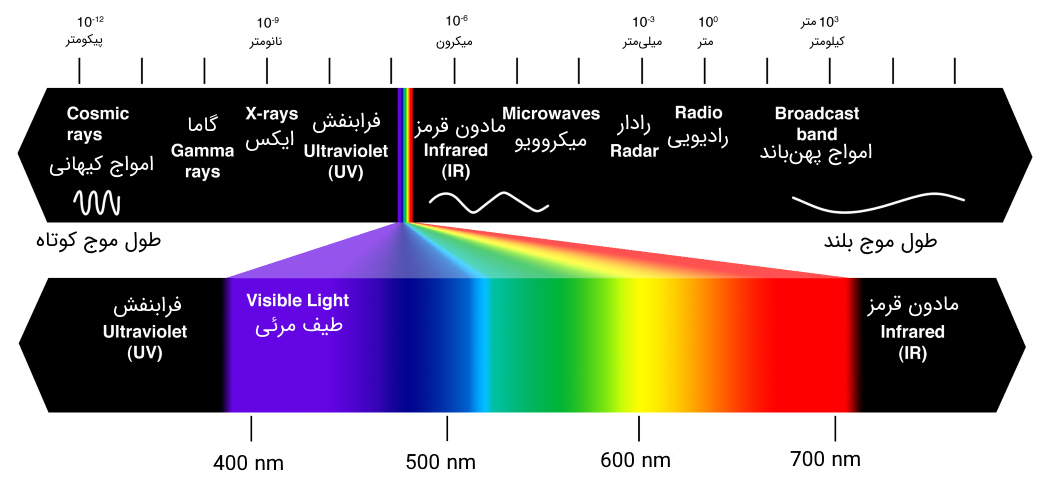
به عبارت دیگر، مطابق با شکل فوق هرچه به سمت امواج ایکس و گاما در طیف الکترومغناطیسی پیش میرویم، طول موج کاهش یافته و انرژی فوتون وابسته به امواج بیشتر میشود. در رابطه فوق، سرعت نور در خلأ (ضریب شکست یک) است.
مقدار انرژی فوتون غالباً با واحد الکترون ولت () بیان میشود. جهت تبدیل واحد انرژی ژول () به الکترون ولت ()، کافی است که مقدار ژول به دست آمده را بر مقدار بار الکترون، یعنی ، تقسیم کنید. واضح است که برای تبدیل واحد الکترون ولت () به ژول، مقدار الکترون ولت را در بار الکترون ضرب میکنیم.
(7)
به عبارت دیگر یک الکترون ولت، مقدار انرژی است که یک الکترون، تحت ولتاژ ۱ ولت دارد. در فیزیک، جرم اجسام را بنا بر رابطه همارزی جرم و انرژی () بر حسب الکترون ولت نیز بیان میکنند.
در مسائل فیزیک مدرن جهت راحتی کار، انرژی فوتون را به صورت زیر مینویسند:
(8)
عبارت در واقع حاصل ضرب ثابت پلانک در سرعت نور است که به مقدار بار الکترون نیز تقسیم شده است. یعنی:
(9)
با توجه به رابطه (8)، در صورتی که طول موج را با واحد آنگستروم () در رابطه بگذارید، محاسبات سر راستی خواهید داشت. همچنین حاصل ضرب بر حسب میکرو الکترون ولت () به صورت زیر در است.
(10)
عبارت فوق بیان میکند که موج الکترومغناطیسی با فرکانس حدود ۱ میکرومتر که در ناحیه فروسرخ (infrared) قرار دارد، انرژی فوتون وابسته آن 1.2398 الکترون ولت است. در شکل زیر حدود انرژی فوتون وابسته به امواج الکترومغناطیسی نشان داده شده است.
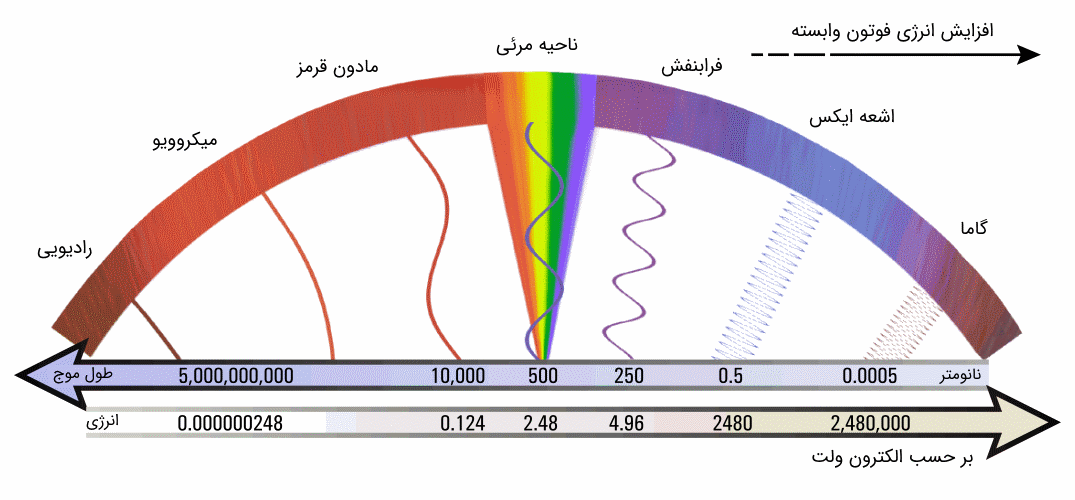
در ادامه چند مثال از مبحث فوق را ارائه میکنیم.
ایستگاه رادیویی (Radio Station)
یک آنتن فرستنده رادیویی FM که در فرکانس امواج الکترومغناطیسی (میدانهای الکتریکی و مغناطیسی عمود برهم) را تابش میکند، در واقع فوتونهایی با انرژی ساطع میکند. این مقدار انرژی مطابق با رابطه همارزی جرم و انرژی ()، حدود برابر جرم یک الکترون است.

فوتوسنتز (Photosynthesis)
در حین انجام عمل فوتوسنتز توسط گیاهان، مولکولهای کلروفیل (chlorophyll)، فرکانسهای نزدیک باند قرمز از طیفمرئی، یعنی فوتونهایی با طول موج تقریبی 700 نانومتر را جذب میکنند.

انرژی هر فوتون در طول موج مذکور مطابق با رابطه (6)، در حدود مقدار زیر است:
در رابطه فوق، حاصل ضرب ثابت بولتزمن (Boltzmann constant) با مقدار ، در دما (بر حسب کلوین) واحد انرژی حرارتی است. جهت سنتز مولکول گلوکوز (Glucose) از آب و با اختلاف پتانسیل شیمیایی و راندمان تبدیل انرژی ۳۵ درصد، حداقل به 48 فوتون نیاز است.
امواج پر انرژی گاما (VHEGR)
با افزایش فرکانس امواج الکترومغناطیسی، مطابق با طیف الکترومغناطیسی به امواج گاما میرسیم. امواج گاما به دلیل انرژی زیادی که دارند برای بدن انسان خطرناک بوده و بررسی آنها شرایط آزمایشگاهی خاصی را طلب میکند.
امواج بسیار پر انرژی گاما (Very High Energy Gamma Ray : VHEGR) که خود در انتهای ناحیه گاما قرار دارند، انرژی در حدود 100 گیگا الکترون ولت تا 100 ترا الکترون ولت () یا حدود 16 نانوژول تا 16 میکروژول دارند. به عبارت دیگر، فرکانس امواج مذکور در محدوده () است. همچنین این امواج مطابق با رابطه () طول موج بسیار کوچکی در محدوده () دارند.
منابع امواج مذکور که محدوده بزرگی از پرتوهای کیهانی (Cosmic Ray) را تشکیل میدهند، ستارههای بسیار داغ (پلاسمای چگال) هستند. به طور مثال تابشهای ساطع شده از ستاره Cygnus X-3 دارای انرژیی در محدوده گیگا الکترون ولت تا اگزا الکترون ولت را شامل میشود.
اثر فوتوالکتریک (Photoelectric Effect)
در دو مقاله «اثر فوتوالکتریک -- به زبان ساده» و «فوتوسل -- به زبان ساده» با فیزیک پدیده مذکور آشنا شدید. دیدیم که جهت آزاد شدن الکترونها از سطح فلز (موسوم به فوتوالکترون)، به فوتونی با حداقل انرژی تابع کار فلز نیاز است. در واقع مطابق با رابطه اینشتین، انرژی فوتون تابشی () باید بیشتر از تابع کار فلز () باشد تا مقداری انرژی برای الکترون در شکل انرژی جنبشی باقی بماند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر را نیز به شما پیشنهاد میکنیم:













سلام
آیا می شود انرژی دقیق نور سفید را به دست آورد؟
سلام
آیا انرژی فوتون نور در هوا یا آب یکسان است؟!
یعنی n مقدار ثابتی هست؟
به نظر من رفتار ذره ای نور اشتباه است و چرا چون مثلا فکر کنید که لامپ ال ای دی داره ذره تولید می کنه
یعنی ما تو راکتور اتمی یا آزمایشگاه نتونستیم ذره تولید کنیم انوقت یک لامپ داره تولید می کنه
مسخره هستش
نور کاملا موجی هست . و این قضیه ی ذره اشتباه است
با سلام،
به این نکته توجه داشته باشید که رفتار ذرهای یا موجی نور هر دو صحیح است. به عنوان مثال، هنگامی که اثر فوتوالکتریک را توضیح میدهیم نور را به صورت بستههای انرژی در نظر میگیریم. همچنین، ذراتی مانند الکترون نیز رفتار موجی خواهند داشت. این رفتار دوگانه موجی-ذرهای پایهترین اساس فیزیک کوانتوم است.
با تشکر از همراهی شما با مجله فرادرس
پتانسیلی که فوتون در هنگام ورود از هوا به شیشه به آن برخورد می کنه چیه؟
عزیز ثابت پلانک رو اشتباه نوشتین
6.626 باید باشه
ولی نوشتین 1.626
سلام و روز شما به خیر؛
این مورد در متن مورد بازبینی و ویرایش قرار گرفت.
از اینکه با مجله فرادرس همراه هستید خرسندیم.