میدان مغناطیسی جریان — از صفر تا صد

پیش‌تر در وبلاگ فرادرس میدان مغناطیسی را تعریف کردیم و مفاهیم آن را شرح دادیم. در مطلب مذکور تشریح کردیم که چگونه حرکت ذرات منجر به ایجاد میدان مغناطیسی می‌شود. در این قسمت قصد داریم تا حالت‌های مختلف این حرکت را بررسی کنیم و در نتیجه میدان ناشی از جریان را بدست آوریم.

قانون بیو-ساوار (Biot–Savart law)

همان‌طور که در بالا نیز بیان کردیم، با به حرکت درآمدن ذرات باردار، میدان مغناطیسی بوجود خواهد آمد. به‌منظور بدست آوردن میدان ناشی از سیم حامل جریان I، بایستی میدان ناشی از حرکت دیفرانسیل بار را بدست آورد و با جمع زدن آن‌ها، میدان ناشی از کل سیم محاسبه خواهد شد. مطابق با شکل زیر برای بدست آوردن میدان مغناطیسی، در ابتدا جزئی برداری برابر با $$\overrightarrow{ds}$$ در نظر می‌گیریم.

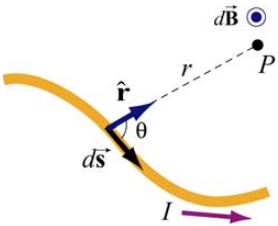
جریان موجود در دیفرانسیل ds برابر با $$I\overrightarrow{ds}$$ است. مطابق با شکل ۱ فرض کنید می‌خواهیم میدان مغناطیسی ناشی از سیم مفروض را در نقطه P بدست آوریم. از این رو در ابتدا بردار $$\overrightarrow{r}$$ را در نظر بگیرید که ابتدای آن در ds و انتهای آن در نقطه P قرار دارد. قانون «بیو-ساوار» (‌Biot-Savart) دیفرانسیل بردار میدان مغناطیسی را با استفاده از رابطه زیر توصیف می‌کند.

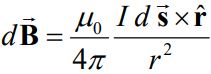
$${\mu_0}$$، تراوایی خلا را نشان می‌دهد و مقدار آن برابر است با:

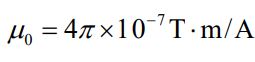
رابطه ارائه شده توسط بیو-ساوار بسیار مشابه با رابطه‌ای است که میدان الکتریکی ناشی از دیفرانسیل بار را نشان می‌دهد. منظور ما رابطه زیر است.

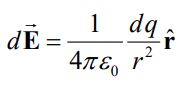
با انتگرال‌گیری از رابطه ۱، میدان ناشی از سیم حاوی جریان I برابر می‌شود با:

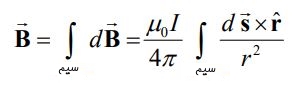
عبارت بالا رابطه‌ای برداری انتگرالی است. از این رو می‌توان گفت که عبارت مذکور ۳ رابطه را نشان می‌دهد [راستای x,y,z].

مثال ۱: میدان ناشی از سیم

مطابق با شکل زیر سیمی را تصور کنید که جریان I در آن جابجا می‌شود.

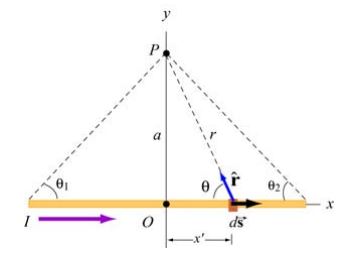
میدان مغناطیسی حاصل از سیم مفروض در نقطه P چقدر است؟

جهت محاسبه میدان مغناطیسی به ترتیب زیر عمل می‌کنیم.

در قدم اول دیفرانسیل سیم را به صورت $$\overrightarrow{ds}=dx'\widehat{i}$$ در نظر می‌گیریم؛ بدیهی است که جریان موجود در این دیفرانسیل برابر با I است. با توجه به شکل ۱ مکان این دیفرانسیل برابر است با:

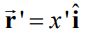
مطابق با شکل ۱ مختصات نقطه P برابر با (x,y)=(0,a) است؛ بنابراین بردار توصیف کننده نقطه P به شکل زیر است.

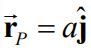
از طرفی بردار $$\overrightarrow{r}=\overrightarrow{r_p}-\overrightarrow{r^ \prime}$$ نشان دهنده موقعیت نقطه P نسبت به دیفرانسیل سیم است. از این رو بردار r را می‌توان به شکل زیر بیان کرد:

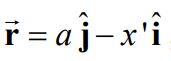
بنابراین اندازه این بردار برابر است با:

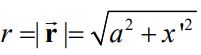
جهت انتگرال‌گیری از رابطه ۱ بهتر است تا عبارت زیر انتگرال را بر حسب بردار یکه $$\widehat{r}$$ نشان داد. بردار یکه $$\widehat{r}$$ را می‌توان با تقسیم بردار r به اندازه آن بدست آورد. در نتیجه داریم:

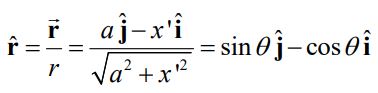
با بیان کردن دو بردار ds و r، حاصلضرب خارجی آن‌ها را نیز می‌توان مطابق با رابطه زیر بدست آورد.

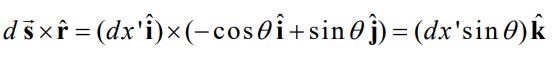
با استفاده از ضرب خارجی بدست آمده در بالا، رابطه ۱ برابر است با:

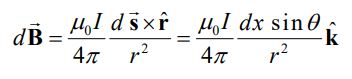
رابطه بالا نشان می‌دهد که میدان بدست آمده در جهت بیرون صفحه است ($$\widehat{k}$$). در قدم بعدی متغیر‌ها را بایستی در مختصاتی بیان کرد که انتگرال‌گیری ساده باشد. از این رو مطابق با دو رابطه زیر r و x را بر حسب $$\theta$$ بیان می‌کنیم:

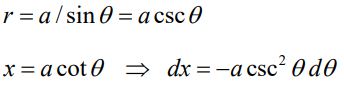
با تغیر متغیر ارائه شده در بالا، رابطه ۱ به شکل زیر قابل بازنویسی می‌شود.

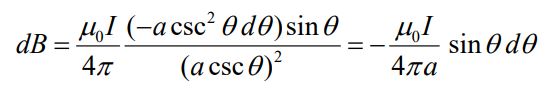
با انتگرال‌گیری از رابطه بالا در بازه $$-\theta_1$$ تا $$\theta_2$$، میدان مغناطیسی برابر با رابطه زیر بدست می‌آید.

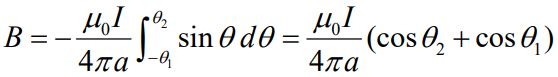
حالتی را تصور کنید که در آن $$-\theta_1=\theta_2$$ باشد. با فرض این‌که طول میله برابر با 2L باشد، می‌توان گفت:

با جایگذاری عبارت بالا در رابطه ۲، داریم:

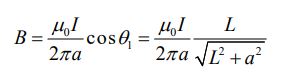
در حالتی که طول L را به بینهایت میل دهیم، میدان الکتریکی در فاصله a از میله برابر می‌شود با:

با توجه به رابطه بالا، میدان الکتریکی در اطراف یک سیم حامل جریان به صورت زیر خواهد بود.

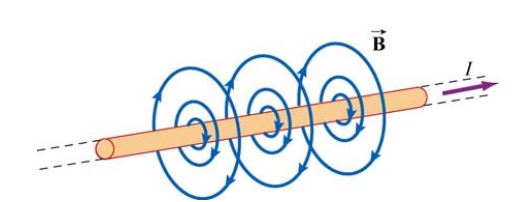
در حقیقت جهت میدان مغناطیسی در اطراف یک سیم را می‌توان با استفاده از قانون دست راست بدست آورد. میدان ناشی از جریانی که به بیرون صفحه جریان دارد، در شکل زیر نشان داده شده است.

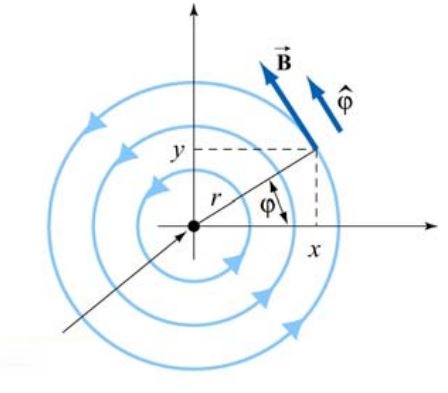
برای تعیین میدان مغناطیسی اطراف یک سیم مطابق با شکل زیر انگشست شست خود را در جهت جریان قرار دهید. در این حالت جهت انگشتان بسته شما، جهت میدان مغناطیسی را نشان می‌دهد.

مثال ۲: میدان ناشی از حلقه حاوی جریان

مطابق با شکل زیر حلقه‌ای به شعاع R را در نظر بگیرید که در صفحه x-y قرار گرفته و جریان I در آن حرکت می‌کند.

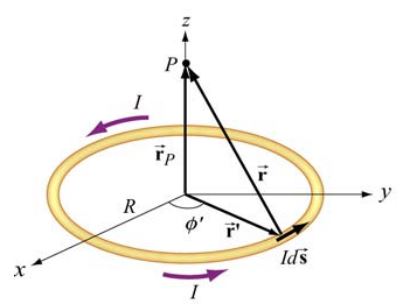
با این فرض موارد زیر مطلوب است:

1. میدان مغناطیسی در نقطه P در فاصله z از مرکز حلقه را بیابید.
2. اگر یک دو قطبی مغناطیسی به اندازه $$\overrightarrow{\mu}=\overrightarrow{\mu}_z\widehat{k}$$ را در میدان ناشی از سیم قرار دهیم، اندازه نیروی وارد شده به آن را بیابید؟

محاسبه میدان در نقطه P

همانند مثال ۱ در این مسئله نیز در ابتدا بایستی کمیت موجود در انتگرال را به‌صورت برداری تعریف کرد؛ از این رو جریان دیفرانسیلی از سیم که در $$\overrightarrow{r^ \prime}=R[Cos(\phi^{\prime}) \widehat{i}+sin(\phi^{\prime}) \widehat{j}]$$ قرار گرفته، برابر است با:

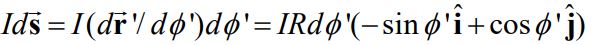
در قدم بعدی بایستی موقعیت نقطه P را نیز به صورت برداری و به شکل زیر بیان کنیم:

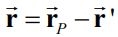
با توجه به دو بردار بدست آمده در مراحل قبل، بردار موقعیت نسبی برابر است با:

همان‌طور که قبلا نیز بیان شد، به‌منظور بدست آوردن بردار یکه r بایستی اندازه آن محاسبه شود. اندازه بردار r برابر با مقدار زیر است.

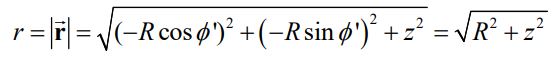
مقدار بالا فاصله بین دیفرانسیل جریان و نقطه P را نشان می‌دهد. در نتیجه بردار یکه r برابر است با:

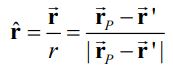
در قدم بعدی بایستی حاصلضرب خارجی بردار موقعیت نسبی (r) و جهت دیفرانسیل جریان را بدست آوریم. این عبارت مطابق با رابطه زیر بدست می‌آید.

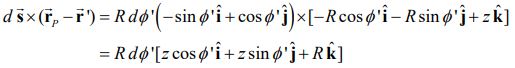
با قرار دادن ضرب خارجی بالا در رابطه بیو-ساوار داریم:

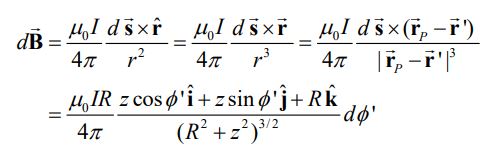
در نتیجه میدان B برابر است با:

می‌توان به شکل زیر نشان داد که مولفه x و y میدان برابر با صفر هستند. البته با استفاده از تقارن نیز این نتیجه قابل دست‌یابی است.

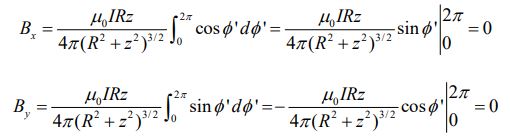
احتمالا متوجه شده‌اید که فقط مولفه z میدانِ بوجود آمده غیرصفر است که مقدار آن برابر است با:

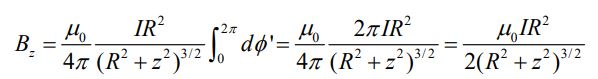
با توجه به رابطه بدست آمده، میدان در z=0 - یا مرکز حلقه - برابر با $$B_0=\large \frac {\mu_oI}{2R}$$ است. نمودار مربوط به میدان بدست آمده برابر است با:

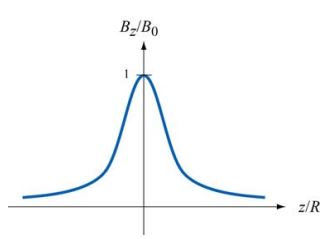
با توجه به شکل بالا و هم‌چنین رابطه بدست آمده برای میدان، می‌توان گفت که اندازه آن در مرکز حلقه ماکزیمم و در فواصل بسیار دور، میدان مغناطیسی برابر با صفر است.

نیروی وارد به دوقطبی

اگر یک دوقطبی مغناطیسی برابر با $$\mu=\mu _z \widehat{k}$$ در نقطه P قرار گیرد، با توجه به مطلب مقدمه‌ میدان مغناطیسی، نیروی وارد به دوقطبی مفروض برابر است با:

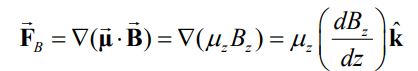
در نتیجه با مشتق‌گیری و جایگذاری میدان بدست آمده در رابطه بالا، نیروی F_B برابر می‌شود با:

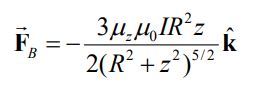
میدان مغناطیسی ناشی از بار متحرک

فرض کنید که در بخشی از یک سیم استوانه‌ای به طول ds و سطح مقطع A، بارهای الکتریکی با نرخ n در واحد حجم در آن جریان دارند. اگر I را برابر با نرخ بار‌های عبوری در واحد زمان در نظر بگیریم، با توجه به مطلب جریان و مقاومت الکتریکی می‌توان گفت:

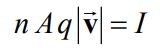
با توجه به پارامتر‌های تعریف شده، کل بار عبوری در سیم برابر با dN=nAds است. در نتیجه با استفاده از قانون بیو-ساوار میدان دیفرانسیلی ناشی از حرکت dN بار الکتریکی در این سیم، برابر است با:

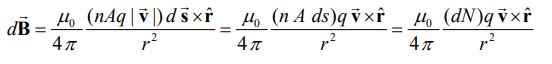
در رابطه بالا r نشان دهنده فاصله بین بارهای الکتریکی و نقطه P است. توجه داشته باشید که $$\overrightarrow{ds}$$ در جهت حرکت جریان و سوی $$\widehat{r}=\overrightarrow{r}/r$$، از سمت بار به نقطه‌ای است که می‌خواهیم میدان الکتریکی را در آن محاسبه کنیم. برای نمونه در حالتی که dN=1 باشد، رابطه بالا به شکل زیر در می‌آید.

توجه داشته باشید که با توجه به نسبیت انیشتین رابطه بالا در حالاتی صادق است که سرعت حرکت ذره بسیار بسیار کمتر از سرعت نور باشد (v<<c).

نیروی بین دو سیم حامل جریان

در بالا توضیح دادیم که چگونه یک سیم حامل جریان در اطراف خود میدانی مغناطیسی ایجاد می‌کند. در مطلب مقدمه میدان مغناطیسی نیز عنوان شد که اگر باری در یک میدان الکتریکی حرکت کند، نیرویی مغناطیسی به آن وارد خواهد شد؛ از این بیان نتیجه می‌شود که به سیم حامل جریان قرار گرفته در میدان مغناطیسی نیز نیرویی وارد خواهد شد. در این قسمت قصد داریم تا نیرو را بدست آورده و در مورد آن بحث کنیم.

در ابتدا مطابق شکل زیر دو سیم حامل جریان I₁ و I₂ را در نظر بگیرید که در فاصله a از یکدیگر قرار گرفته‌اند.

هرکدام از این سیم‌ها در محل سیمِ دیگر، میدان مغناطیسی به وجود آورده و باعث می‌شود به سیم دوم نیرو وارد کند. با توجه به مثال ۲ می‌دانیم که میدان ایجاد شده در محل سیم ۱، ناشی از سیم ۲ برابر است با:

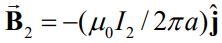
مطابق با شکل ۳ این میدان به‌صورت عمود به سیم ۱ است. در نتیجه نیروی وارد به سیم شماره ۱ از طرف سیم شماره ۲ برابر است با:

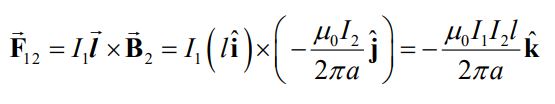
نیروی وارد به سیم ۲ از طرف سیم ۱ نیز دقیقا برابر با همین اندازه و در جهت مخالف است. هم‌چنین بایستی بدانید که اگر جریان درون دو سیم در یک جهت باشند، یکدیگر را جذب و اگر جهت جریان آن‌ها مخالف هم باشد، همدیگر را دفع می‌کنند.

قانون آمپر

تاکنون عنوان کردیم که حرکت بار‌های الکتریکی، میدان مغناطیسی به‌وجود می‌آورد. این میدان را می‌توان با قرار دادن مجموعه‌ای از قطب‌نماها در اطراف یک سیم حامل جریان نشان داد. همانند شکل زیر در حالتی که جریانی در سیم برقرار نباشد، تمامی قطب‌نماها در یک جهت هستند. از طرفی در حالتی که $$I \neq0$$ باشد، قطب‌نماها جهت مماس به میدان مغناطیسی را نشان می‌دهند.

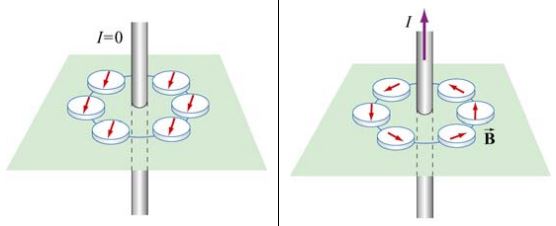
حال اجازه دهید تا مطابق با شکل زیر مسیر دایره‌ای اطراف سیم حامل جریان را به بردارهایی به صورت $$\triangle \overrightarrow{s}=\triangle s\widehat{\phi}$$ تقسیم‌بندی کنیم. اندازه این بردارها برابر با Δs و جهت آن مماس با میدان مغناطیسی در نظر گرفته می‌شود.

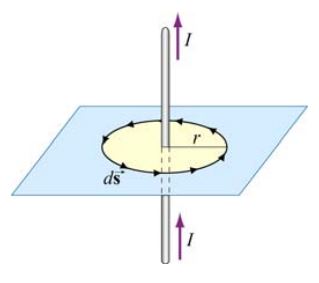
در حالتی حدی که $$\triangle \overrightarrow{s} \rightarrow \overrightarrow{0}$$ است، انتگرال میدان روی مسیر بسته اطراف سیم حامل جریان برابر است با:

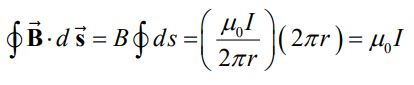
رابطه بالا را می‌توان برای هر مسیر بسته‌ دیگری که سیم حامل جریان I در آن قرار گرفته، نوشت. در حقیقت حاصل این انتگرال در تمامی مسیر‌های نشان داده شده در شکل زیر برابر با $$\mu_0I$$ است. چنین حلقه‌ای را «حلقه آمپری» (Amperian Loop) می‌نامند.

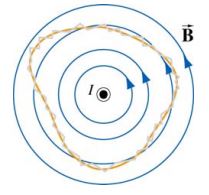
در حالتی عمومی انتگرال میدان مغناطیسی روی یک مسیر بسته،‌ با استفاده از «قانون آمپر» (Amper Law) قابل محاسبه است. این قانون می‌گوید:

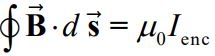
احتمالا شما نیز متوجه تشابه این قانون با قانون گاوس شده‌اید. در حقیقت قانون آمپر ارتباط بین میدان مغناطیسی و جریان‌های قرار گرفته در حلقه آمپر و قانون گاوس ارتباط بین میدان الکتریکی و بار‌های قرار گرفته در سطح بسته را بیان می‌کند.

توجه داشته باشید که قانون آمپر در حالتی که منبع جریان از تقارن مشخصی برخوردار باشد و در حالتی که فرض سیم بی‌نهایت در نظر گرفته شده، مورد استفاده قرار می‌گیرد. اما در شرایط عمومی که با سیمی متناهی روبرو هستیم، جهت محاسبه میدان مغناطیسی بایستی از قانون بیو-ساوار استفاده کرد.

به طور خلاصه قانون آمپر در موارد زیر کاربرد دارد:

• محاسبه میدان ناشی از سیمی بی‌نهایت که جریان I را در حالت پایا در خود حمل می‌کند.
• صفحه‌ای بینهایت به ضخامت b و با چگالی جریان J
• محاسبه میدان مغناطیسی ناشی از «سلونوئید» (Solenoid) بی‌نهایت

جهت آشنایی با نحوه به‌کارگیری قانون آمپر به مثالی که در ادامه آمده توجه کنید.

مثال ۳: میدان درون و بیرون سیم حامل جریان

مطابق با شکل زیر سیمی بلند به شعاع R و جریان I را در نظر بگیرید که چگالی جریان در آن بصورت یکنواخت است. با توجه به این فرضیات میدان مغناطیسی درون و بیرون سیم را بدست آورید.

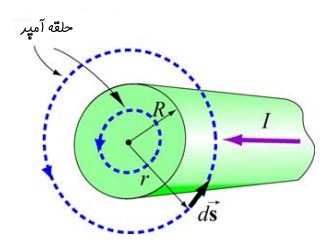
برای بدست آوردن میدان مغناطیسی در ابتدا بایستی حلقه آمپری مناسبی را انتخاب کنیم که این حلقه را دایره‌ای به شعاع $$R$$ در نظر می‌گیریم.

• در حالت اول یا خارج از حلقه آمپری، حلقه‌ای به شعاع r را فرض می‌کنیم که در آن r>R است. برای این حلقه، قانون آمپر مطابق با رابطه زیر نوشته می‌شود:

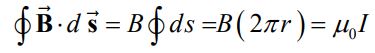
با توجه به رابطه بالا میدان مغناطیسی برابر با عبارت زیر بدست می‌آید.

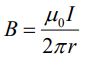
همان‌طور که در شکل نیز مشخص است کل جریان موجود در حلقه با شعاع $$R$$ در حلقه‌ای با شعاع $$r>R$$ محصور است و در نتیجه میدان به راحتی به دست می‌آید.

• در حالت دوم، یعنی زمانی که بخواهیم میدان درون سیم حامل جریان را به دست آوریم، شعاع کوچکتر از شعاع حلقه آمپری است و داریم:

$$r$$

در این حالت قسمتی از جریان حلقه آمپری در این حلقه قرار دارد. میزان جریان موجود در درون سیم حامل جریان برابر است با:

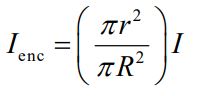
منظور از $$I_{enc}$$، سهم جریان موجود در حلقه‌ای با شعاع کوچکتر از شعاع آمپری است. بدین ترتیب داریم:

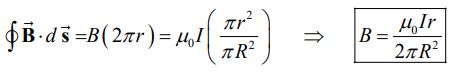
با توجه به رابطه بالا میدان مغناطیسی در مرکز سیم یعنی $$r=0$$ برابر با صفر و در r=R به ماکزیمم مقدار خود می‌رسد. همان‌طور که نمودار زیر نشان می‌دهد، میدان درون سیم به شکلی خطی تغییر می‌کند و میدان خارج از سیم، به‌صورت معکوس با r کم می‌شود.

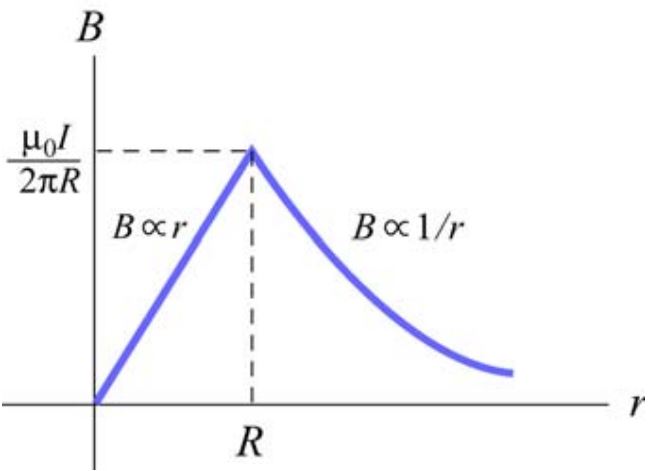
مثال ۴ (مهم): میدان ناشی از صفحه بینهایتِ حامل جریان

مطابق با شکل زیر صفحه‌ای بینهایت به ضخامت b را در نظر بگیرید که چگالی جریانِ آن یکنواخت و برابر با $$\overrightarrow{J}=J_0 \widehat{i}$$ است.

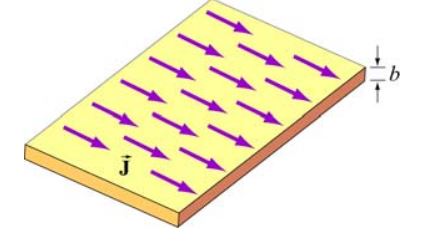
جهت ساده‌سازی مسئله می‌توان صفحه را معادل با بینهایت سیم حامل جریان در نظر گرفت. مطابق با شکل زیر، میدان مغناطیسی در جهت y- است. نقاط نشان داده شده در صفحه، جهت میدان مغناطیسی را به بیرون از صفحه نشان می‌دهند. هم‌چنین با توجه به دایره‌های ترسیم شده در این شکل، مشاهده می‌شود برآیند میدان سیم‌ها در راستای z همدیگر را خنثی می‌کنند.

جهت بدست آوردن میدان مغناطیسی، دو حلقه آمپری C₁ و C₂ را مطابق با شکل زیر در نظر بگیرید.

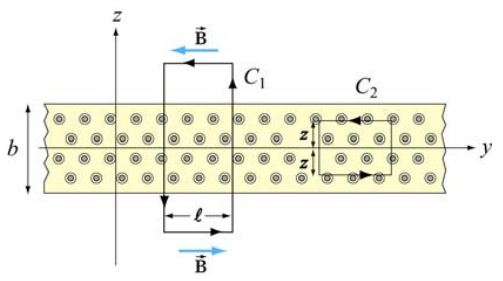
در شکل بالا می‌بینید که دو مسیر C₁ و C₂ ترسیم شده‌اند. از C₁ جهت محاسبه میدان بیرون از صفحه و از C₂ جهت بدست آوردن میدان درون صفحه استفاده خواهیم کرد. مقدار جریان قرار گرفته درون حلقه C₁ با انتگرال‌گیری از چگالی جریان،‌ به صورت زیر قابل محاسبه است.

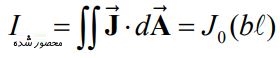
حال با اعمال قانون آمپر روی حلقه C₁ داریم:

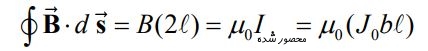
در نتیجه میدان مغناطیسی در بیرون از صفحه برابر است با:

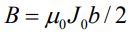
نکته جالب پاسخ بالا این است که میدان در بیرون از صفحه و در تمامی نقاط با یکدیگر برابر هستند. همانند مسیر C₁، جریان قرار گرفته در مسیر C₂ برابر است با:

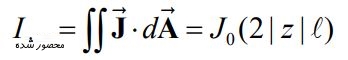
قانون آمپر برای مسیر C₂ به شکل زیر قابل بیان است:

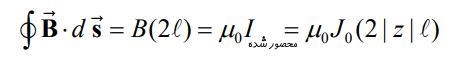
در نتیجه میدان مغناطیسی درون سیم برابر است با:

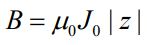
به‌منظور ایجاد تقارن، میدان مغناطیسی در z=0 برابر با صفر است. نهایتا میدان مغناطیسی را می‌توان به صورت برداری و به شکل زیر نشان داد.

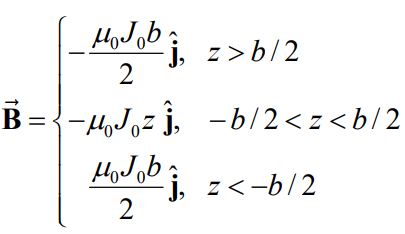
در حالتی حدی که صفحه بسیار نازک است ($$b \rightarrow 0$$)، به جای تعریف چگالی حجمی جریان از مفهومی تحت عنوان چگالی سطحی استفاده می‌شود. چگالی سطحی را با $$\overrightarrow{K}=K \widehat{i}$$ نشان داده که در آن K=J₀b است. نهایتا در حالتی که با صفحه بسیار نازکی با چگالی سطحی K مواجه‌ایم، میدان مغناطیسی ناشی از آن برابر با رابطه زیر است.

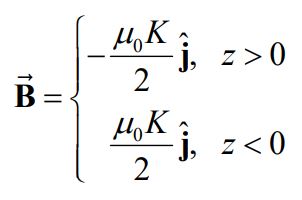
سلونوئید (Solenoid)

سلونوئید به حلقه‌‌هایی سیمی گفته می‌شود که معمولا دور یک هسته‌ فلزی پیچیده شده‌اند. با وصل کردن سلونوئید به یک اختلاف ولتاژ، جریانی الکتریکی در آن برقرار خواهد شد که منجر به تولید میدان مغناطیسی می‌شود. شکل زیر دو نما از یک سلونوئید را نشان می‌دهد.

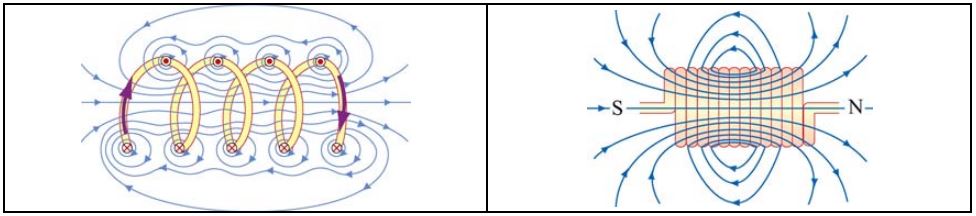
مشاهدات نشان داده که اگر حلقه‌های سلونوئید به یکدیگر نزدیک باشند، میدان مغناطیسی در آن به میزان قابل قبولی یکنواخت خواهد بود. در حقیقت در این حالت طول سلونوئید بسیار بیشتر از قطر آن است. برای سلونوئیدی که به صورت فشرده پیچیده شده، میدان مغناطیسی درون آن در راستای محورِ سلونوئید و یکنواخت است.

اندازه میدان مغناطیسی درون سلونوئید با استفاده از قانون آمپر قابل محاسبه است. در شکل زیر مقطع سلونوئیدی ایده‌آل نشان داده شده است. ردیف بالا میدان به بیرون صفحه و ردیف پایین، میدان درون صفحه را نشان می‌دهند.

مطابق با تصویر بالا مسیری مستطیلی شکل با طول l و عرض w در سلونوئید در نظر گرفته شده و برای انتگرال‌گیری، به صورت پادساعتگرد روی آن حرکت می‌کنیم. در نتیجه از آنجایی که جهت میدان مغناطیسی در راستای محور سلونوئید در نظر گرفته شده، بنابراین حاصل انتگرال میدان مغناطیسی روی مسیر‌های ۲ و ۴ برابر با صفر است. در نتیجه انتگرال روی مسیر بسته‌ مفروض به شکل زیر محاسبه می‌شود.

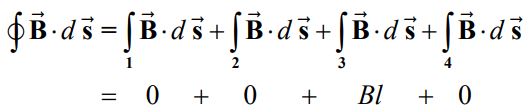
رابطه بالا با این فرض نوشته شده که میدان فقط بیرون از سلونوئید غیرصفر فرض شده باشد؛ به این خاطر است که انتگرال روی مسیر ۱ برابر با صفر در نظر گرفته شده. هم‌چنین از شکل ۴ نیز واضح است که میزان جریان قرار گرفته درون حلقه آمپر برابر با I_enc=NI است. N تعداد حلقه‌های سلونوئید و I جریان حلقه‌ها است. در نتیجه قانون آمپر (رابطه بالا) به صورت زیر در می‌آید.

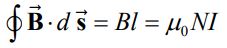
با توجه به رابطه بالا، میدان مغناطیسی، برابر است با:

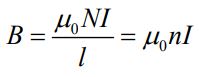
در رابطه بالا n=N/l است که نشان دهنده تعداد حلقه‌ها در واحد طول سلونوئید است. این رابطه در حالتی بدست آمده که طول سلونوئید بینهایت فرض شده است. در حالتی که این طول متناهی باشد، توزیع میدان مغناطیسی به چه شکل خواهد بود؟

جهت بدست آوردن میدان درون سلونوئیدی متناهی، تعداد حلقه‌های سلونوئید را زیاد و متراکم فرض کنید. در مثال ۲ میدان مغناطیسی در فاصله عمودی z از مرکز یک حلقه را برابر با مقدار زیر یافتیم.

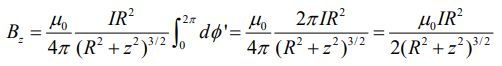
مطابق با شکل زیر جزئی دیفرانسیلی به طول 'dz را در نظر بگیرید که در موقعیت z قرار گرفته است. در حقیقت حلقه‌ای به شعاع R و ضخامت 'dz در نظر گرفته شده که هدف، محاسبه میدان ناشی از دیفرانسیل 'dz در نقطه P است.

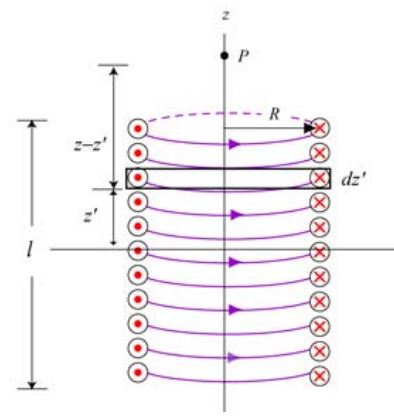
با فرض اینکه چگالی جریان الکتریکی به صورت یکنواخت در نظر گرفته شود، واضح است که میزان جریان موجود در 'dz، متناسب با اندازه آن است. در نتیجه دیفرانسیل جریان در 'dz برابر است با:

در رابطه بالا n=N/l است. در حقیقت n نشان دهنده تعداد حلقه‌ها در واحد طول سنولوئید است. با توجه به نتایج مثال ۲، میدان ناشی از دیفرانسیل 'dz در نقطه P برابر است با:

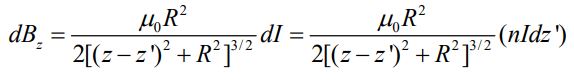
با استفاده از انتگرال‌گیری رابطه بالا روی طول کل سلونوئید، میدان مغناطیسی در P مطابق با رابطه زیر بدست می‌آید.

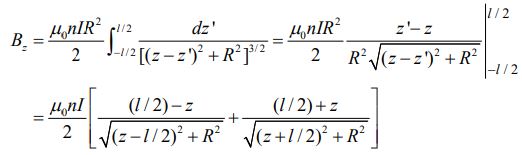
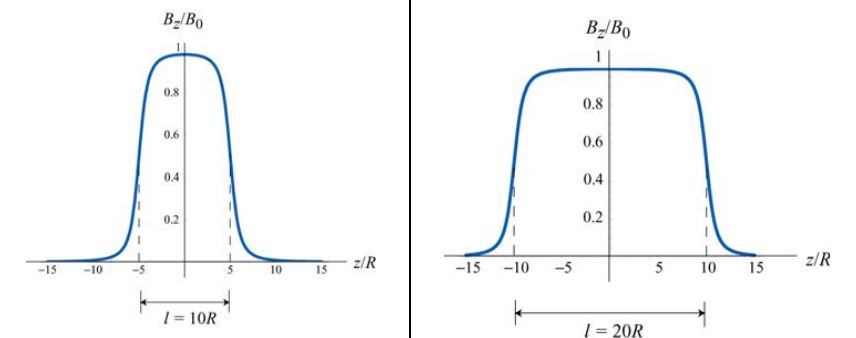
شکل زیر تغییرات تابع B_z/B₀ را برای سلونوئیدی با دو نسبت طول به شعاعِ متفاوت نشان می‌دهد. توجه داشته باشید که B₀ برابر با $$\mu_0nI$$ است. شکل سمت چپ سلونوئیدی با نسبت l/R=10 و سمت راست l/R=20 را نشان می‌دهد.

مثال ۵: سلونوئید حلقوی

مطابق با شکل زیر سلونوئیدی با N حلقه را در نظر بگیرید.

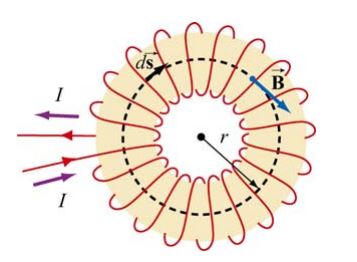
میدان مغناطیسی در وسط حلقه‌ها چقدر است؟

حلقه آمپری را همانند شکل ۵، درون سلونوئید در نظر بگیرید. با توجه به جهت جریان I، جهت میدان مغناطیسی به صورت ساعتگرد است. با فرض این‌که حلقه‌ها فشرده باشند، به این نتیجه می‌رسیم که اندازه میدان درون سلونوئید ثابت است. با نوشتن انتگرال میدان مغناطیسی روی مسیر فرض شده، میدان مغناطیسی برابر با مقدار زیر بدست می‌آید.

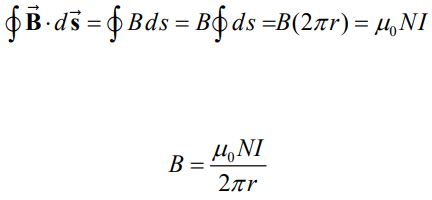
در مطالب آینده ابعادی بیشتر از میدان مغناطیسی را نشان خواهیم داد. در حقیقت یکی از منابع تولید میدان مغناطیسی ایجاد جریان است که در این قسمت آن را توضیح دادیم. البته جهت حل مثال‌های بیشتر و تسلط کامل‌تر به مفاهیم میدان مغناطیسی می‌توانید به این آموزش ویدئویی مراجعه کنید. هم‌چنین در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک پایه و مهندسی برق، احتمالا آموزش‌های زیر می‌توانند برایتان کاربردی باشند:

• مجموعه آموزش‌های فیزیک
• مجموعه آموزش‌های مهندسی برق
• مجموعه آموزشی دروس مهندسی برق
• میدان مغناطیسی چیست؟ به زبان ساده
• قانون دست راست -- به زبان ساده
• فیزیک الکتریسیته را به سادگی و با مجموعه مقالات وبلاگ فرادرس یاد بگیرید