القای فارادی – به زبان ساده

با توجه به مطالب بیان شده در مورد میدان الکتریکی و مغناطیسی دانستیم که این کمیت‌ها به ترتیب در نتیجه بار‌های ساکن و بارهای متحرک الکتریکی ایجاد می‌شوند. از آنجایی که میدان الکتریکی منجر به ایجاد جریان الکتریکی می‌شود، بنابراین احتمالا رابطه‌ای بین آن‌ها وجود دارد. این رابطه در سال ۱۸۳۱، توسط مایکل فارادی (Michael Faraday)،‌ دانشمند انگلیسی کشف شد. او متوجه شد که با تغییر دادن میدان مغناطیسی نسبت به زمان، میدان الکتریکی بوجود خواهد آمد. به این پدیده القای الکترومغناطیسی گفته می‌شود. شکل زیر یکی از آزمایش‌های انجام شده توسط فارادی را نشان می‌دهد.

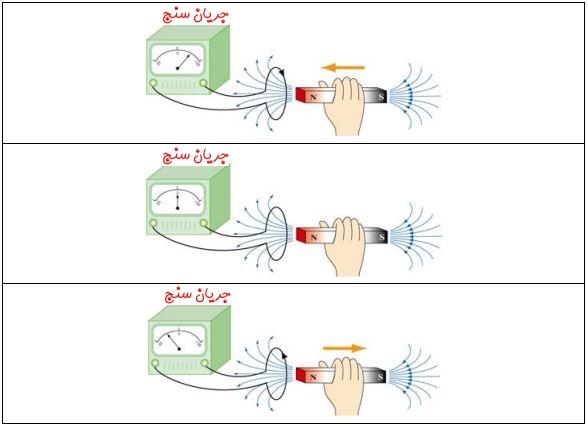
در این آزمایش حلقه‌ای رسانا به یک جریان‌ سنج وصل شده و در این حالت آهنربایی به تدریج به آن نزدیک می‌شود. با انجام این کار مشاهده می‌شود،‌ در زمان حرکت آهنربا، جریانی الکتریکی در سیم ایجاد می‌شود. فارادی در حالت‌های مختلف، مشاهده کرد تا زمانی که آهنربا نسبت به حلقه ساکن است، جریانی تولید نمی‌شود. در حقیقت تغییر میدان مغناطیسی نسبت به زمان منجر به ایجاد جریانی الکتریکی در سیم می‌شود. جهت توضیح کمی‌ این پدیده، در ابتدا نیاز است تا با مفهومی تحت عنوان شار مغناطیسی آشنا باشید که در ادامه به آن‌ اشاره خواهد شد.

شار مغناطیسی

مطابق با شکل زیر میدانی مغناطیسی و یکنواخت را در نظر بگیرید که از صفحه‌ای عبور می‌کند. بردار سطح به‌صورت $$\overrightarrow{A}=A \widehat{n}$$ در نظر گرفته می‌شود. در این فرض A برابر با اندازه سطحی است که میدان مغناطیسی از آن عبور می‌کند.

هم‌چنین $$\widehat{n}$$ بردار عمود به سطح را نشان می‌دهد که به سمت بیرون در نظر گرفته می‌شود. با توجه به این فرضیات، شار گذرنده از سطح، برابر است با:

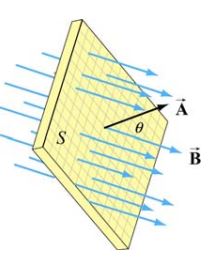
در رابطه بالا θ، زاویه بین بردار‌های $$\widehat{n}$$ و $$\overrightarrow{B}$$ را نشان می‌دهد. در حالتی که میدان یکنواخت نباشد، شار مغناطیسیِ $$\Phi_B$$ برابر است با:

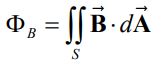
واحد شار مغناطیسی در سیستم SI را «وِبِر» می‌نامند که با Wb نشان داده می‌شود. ۱ وبر برابر است با:

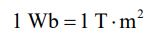
با توجه به تعریف شار مغناطیسی، قانون القای فارادی را می‌توان به صورت زیر توصیف کرد:

نیروی محرکه (ε) ایجاد شده در یک حلقه برابر با منفی تغییرات شار مغناطیسی است که از سطح سیم‌پیچ عبور می‌کند. بنابراین نیرو محرکه ایجاد شده برابر است با:

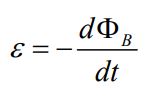
برای سیم‌پیچی که از N حلقه تشکیل شده، نیروی محرکه القا شده برابر است با:

با ترکیب روابط ۱ و ۲، نیرو محرکه القا شده را می‌توان تابعی از تغییرات سطح و زاویه، به شکل زیر بدست آورد.

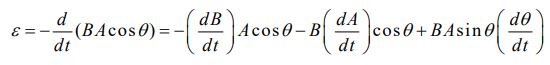
در نتیجه، نیروی محرکه القا شده در یک حلقه تحت شرایط زیر بوجود می‌آید.

1. تغییر میدان مغناطیسی $$\overrightarrow{B}$$ با زمان (شکل زیر)
   
2. تغییر مساحتِ‌ قرار گرفته در معرض میدان مغناطیسی (شکل زیر)
   
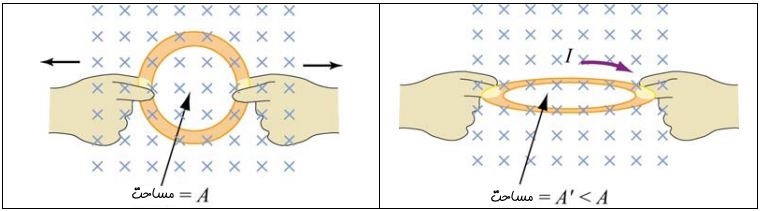
3. تغییر زاویه بین $$\overrightarrow{B}$$ و $$\overrightarrow{A}$$ با زمان (شکل زیر)
   

قانون لنز (Lenz Law)

جهت جریان ایجاد شده در سیم را با استفاده از قانون لنز تعیین می‌کنند. این قانون بیان می‌کند که جریان القا شده در رسانا، میدانی تولید می‌کند که خلاف جهت تغییرات شار مغناطیسی عمل می‌کند. به‌منظور توضیح قانون لنز، مطابق با شکل زیر حلقه‌ای را در نظر بگیرید که در میدانی مغناطیسی قرار گرفته است.

به‌منظور تعیین جهت جریان القا شده به ترتیب زیر عمل کنید:

1. جهت مثبتی برای بردار $$\overrightarrow{A}$$ در نظر بگیرید.
2. با فرض این‌که میدانِ $$\overrightarrow{B}$$ متقارن باشد، حاصلضرب داخلی دو بردار $$\overrightarrow{A}$$ و $$\overrightarrow{B}$$ را بیابید.
3. با مشتق‌گیری از شار بدست آمده در مرحله قبل، نرخ تغییرات آن را نسبت به زمان ($$\large \frac {d\Phi_B}{dt}$$) بدست آورید. سه حالت زیر وجود خواهد داشت:
   

در مرحله آخر با استفاده از قانون دست راست، جهت جریان القاء شده بدست می‌آید. انگشت شست خود را در جهت بردار A بگیرید؛ در این حالت اگر ۰<ε، جهت انگشتان بسته شما، جهت جریان و اگر ۰>ε باشد، جهت جریان القا شده، خلاف جهت انگشتان بسته شما است. با استفاده از ۴ مرحله بالا می‌توانید جهت جریان ایجاد شده در حلقه قرار گرفته در میدان مغناطیسی را بدست آورید. شکل زیر ۴ حالت متفاوت از جریان القا شده در میدان مغناطیسی متغیر را نشان می‌دهد.

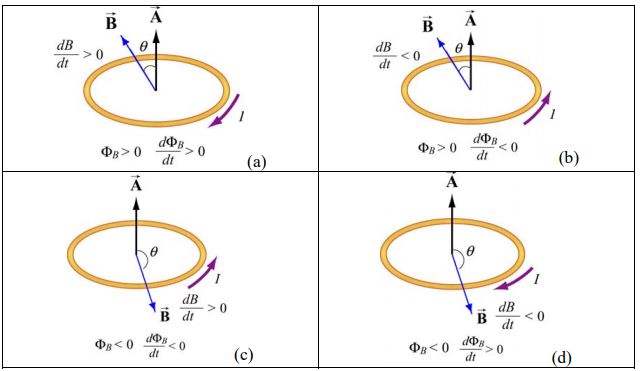
حالات بالا به طور خلاصه در جدول زیر بیان شده‌اند.

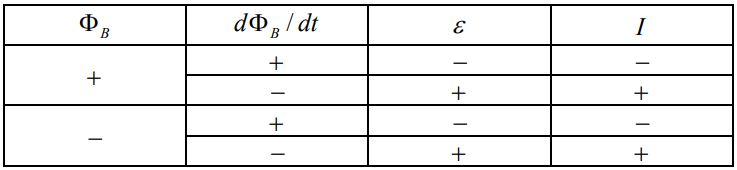
توجه داشته باشید که علامت منفی و مثبتِ جریانِ I، به ترتیب معادل با ساعتگرد و پادساعتگرد بودن جریان الکتریکی است. جهت بررسی نحوه عملکرد قانون لنز، مطابق شکل زیر حلقه‌ای را تصور کنید که آهنربایی از سمت قطب شمالش به آن نزدیک می‌شود.

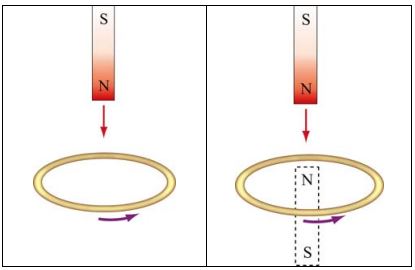
قبلا نیز ذکر کردیم که جهت میدان مغناطیسی یک آهنربا از قطب شمال به قطب جنوبش است. با توجه به این‌که جهت بردار A به سمت بالا و B به سمت پایین است، در نتیجه شارِ $$\Phi_B=-BA<0$$ منفی است. در حالی که آهنربا به سمت حلقه در حال نزدیک شدن است، میدان مغناطیسی عبوری از حلقه نیز با زمان افزایش می‌یابد ($$dB/dt>0$$) که منجر به عبور شار بیشتر با زمان می‌شود. در نتیجه تغییرات شار عبوری از حقله برابر با $$\Large \frac {d\Phi_B}{dt}=-A \Large \frac {dB}{dt}<0$$ است. از این رو با توجه به رابطه القای فارادی، نیرو محرکه القا شده مثبت خواهد بود (ε>0). حال با استفاده از قانون دست راست و این‌که نیرو محرکه بدست آمده مثبت است، جهت جریان القا شده در این حالت، به صورت پادساعتگرد خواهد بود.

شکل زیر قانون لنز را به طور خلاصه نشان می‌دهد.

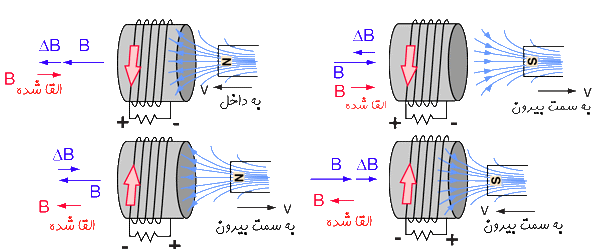
نیروی محرکه ایجاد شده در نتیجه حرکت

همان‌طور که در تصویر زیر نشان داده شده، میله‌ای رسانا را به طول L تصور کنید که در میدانی مغناطیسی در حال حرکت می‌باشد. جهت این میدان به سمت درون صفحه است.

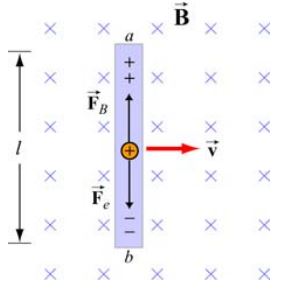
در مطلب مقدمه میدان مغناطیسی عنوان کردیم که به ذره باردار در حال حرکت در میدان مغناطیسی، نیرویی برابر با $$\overrightarrow{F}_B=q \overrightarrow{v}×\overrightarrow{B}$$ وارد می‌شود. در این مورد نیز به ذرات مثبت نیرویی به سمت بالا وارد خواهد شد؛ در نتیجه به نظر می‌رسد میله به دو بخش با ذرات باردار مثبت و منفی تبدیل می‌شود.

با قرار گرفتن بارهای مثبت و منفی در دو سر میله، میدانی الکتریکی ($$\overrightarrow{E}$$) بین آن‌ها بوجود خواهد آمد که منجر به وارد شدن نیرویی برعکس نیروی مغناطیسی به بارها می‌شود [$$\overrightarrow{F}_E=\overrightarrow{E}q$$]. در حالت تعادل، بار‌ها جابجایی خالصی را در میله تجربه نمی‌کنند؛ در نتیجه نیروی ناشی از میدان مغناطیسی (qvB) و میدان الکتریکی (Eq) با یکدیگر برابر خواهند شد. از این رو با برابر قرار دادن آن‌ها داریم:

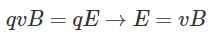
در نتیجه اختلاف پتانسیل ایجاده شده در دو سمت رسانای مفروض، برابر است با:

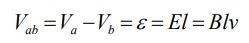
از آنجایی که اختلاف پتانسیل شرح داده شده در نتیجه حرکت رسانا است، بنابراین آن را اختلاف پتانسیل حرکتی می‌نامند. در حالت کلی اختلاف پتانسیل حرکتی ایجاد شده در یک مسیر بسته را می‌توان مطابق با رابطه زیر توصیف کرد.

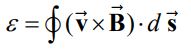
در رابطه بالا $$d \overrightarrow{s}$$ دیفرانسیلِ بردار طول را نشان می‌دهد. حال تصور کنید که میله رسانایی بخشی از یک مدار را مطابق با شکل زیر تشکیل می‌دهد. توجه داشته باشید که میدان مغناطیسی به درون صفحه در نظر گرفته شده و R مقاومت مدار است.

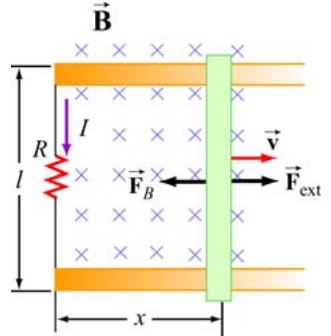
فرض کنید نیروی ثابت F_ext به میله متحرک وارد شود. در نتیجه میله مذکور با سرعت ثابت v به سمت راست حرکت خواهد کرد. از آنجایی که مساحت حلقه متغیر است، بنابراین شار بدست آمده در هر لحظه برابر است با:

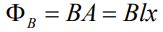
در نتیجه باتوجه به قانون القای فارادی، نیرو محرکه القا شده برابر با مقدار زیر بدست می‌آید.

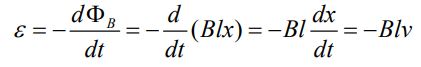
در رابطه بالا dx/dt=v برابر با سرعت میله است؛ جریان القا شده در این مدار را می‌توان مطابق با رابطه زیر بدست آورد.

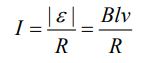
هم‌چنین با توجه به قانون لنز جهت جریان القا شده، پادساعتگرد بدست می‌آید؛ بنابراین حرکت این میله در میدان مغناطیسی مذکور را می‌توان معادل با مداری الکتریکی، به شکل زیر فرض کرد.

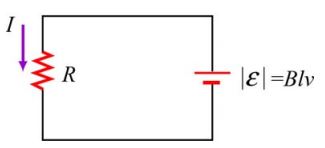
هم‌چنین نیروی وارد شده به میله در هنگام حرکت به سمت راست، برابر است با:

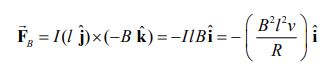
در نتیجه جهت ثابت بودن سرعت v، نیروی مغناطیسی بایستی برابر با نیروی خارجی وارد شده به میله باشد. در حقیقت رابطه بین نیرو‌ها به‌شکل زیر قابل بیان است:

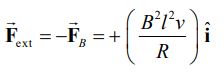
از دیدگاه انرژی، توانی که $$\overrightarrow{F}_{ext}$$ به سیستم می‌دهد برابر است با:

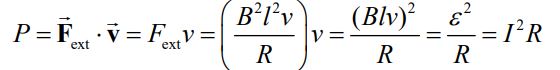
نکته جالب رابطه بالا در این است که توان اضافه شده به سیستم توسط نیروی خارجی برابر با توانی است که در مقاومت الکتریکی تلف می‌شود. بنابراین قانون پایستگی انرژی نیز برای کل سیستم صدق می‌کند.

در بالا مسئله‌ای را در نظر گرفتیم که در آن نیروی خارجی ثابت F_Ext به سیستم وارد می‌شد. حال فرض کنید که در زمان t=0 سرعت اولیه میله برابر با v₀ باشد و ناگهان نیروی خارجی قطع شود. بدیهی است که در این لحظه به دلیل وارد شدن نیروی مغناطیسی به میله، سرعت آن با گذشت زمان کم‌ می‌شود. از قوانین نیوتن داریم:

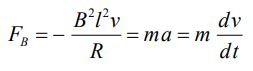
رابطه بالا را می‌توان به شکل زیر نیز بیان کرد:

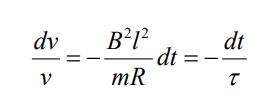
در رابطه بالا τ=mR/B²l² است. با انتگرال‌گیری از طرفین آن، سرعت میله ‌به‌صورت زیر بدست می‌آید.

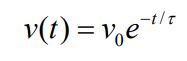
میدان الکتریکی القا شده

در مطلب پتانسیل الکتریکی عنوان کردیم که میدان الکتریکی می‌تواند اختلاف پتانسیلی بین دو نقطه A و B را برابر با مقدار زیر تولید کند.

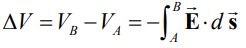
هم‌چنین عنوان شد که برای یک میدان الکتریکی پایسته،‌ انتگرال بالا روی مسیر بسته برابر با صفر است [$$\oint \overrightarrow{E}.\overrightarrow{ds}=0$$]. با توجه به صفر بودن این انتگرال پس چرا بار‌های الکتریکی با تغییر شار مغناطیسی به حرکت در می‌آیند؟ پاسخ در نیرو محرکه القا شده است. در حقیقت در این حالت میدان الکتریکی پایسته نیست، چرا که انتگرال روی مسیر بسته آن غیر صفر است. در نتیجه با فرض این‌که نیروی محرکه القا شده برابر با ε باشد، انتگرال میدان الکتریکی ناپایا (Non Conservative) روی مسیر بسته برابر است با:

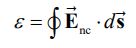
با ترکیب کردن قانون القای فارادی با رابطه بالا داریم:

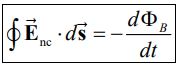
رابطه بالا بیان می‌کند که با تغییر شار مغناطیسی، میدان الکتریکی ناپایایی به‌وجود خواهد آمد که می‌تواند با زمان تغییر کند. این در حالی است که میدان الکتریکی ناشی از بار‌ الکتریکی، میدانی پایا را ایجاد خواهند کرد. جهت درک بهتر، به مثال زیر توجه کنید.

مثال ۱: میدان الکتریکی القاء شده در حلقه

مطابق با شکل زیر میدان مغناطیسی یکنواختی را در نظر بگیرید که جهت آن به سمت درون صفحه است.

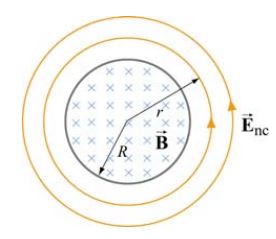
فرض کنید که میدان مغناطیسی مذکور با سرعت ۰<dB/dt نیز افزایش می‌یابد. در این صورت میدان الکتریکی القاء شده در نقاط مختلف این حلقه چقدر است؟

مسیر انتگرال‌گیری جهت یافتن میدان الکتریکی را به‌ شکل حلقه‌ای به شعاع r فرض می‌کنیم. با توجه به تقارن موجود در مسئله میدان القاء شده ($$\overrightarrow{E}_{nc}$$) روی تمامی نقاط این حلقه برابر است. بدیهی است که جهت $$\overrightarrow{E}_{nc}$$ میدان الکتریکی القا شده در جهت جریان الکتریکی القا شده است. اگر بردار A را به‌ سمت درون صفحه تصور کنیم، شار مغناطیسی بدست آمده با زمان افزایش می‌یابد؛ در نتیجه با استفاده از قانون دست راست، جهت جریان الکتریکی القاء شده بایستی در خلاف جهت انگشتانِ بسته باشد. اگر شست خود را در جهت میدان مغناطیسی (درون‌سو) قرار دهیم جهت انگشتان بسته ما به صورت ساعتگرد خواهد بود. در نتیجه جریان القا شده به صورت پادساعتگرد است. در شکل ۲ جهت میدان الکتریکی القاء شده نشان داده شده است.

با تعیین جهت میدان الکتریکی القاء شده، زمان آن رسیده تا اندازه آن را بدست آوریم. در ناحیه r<R، سرعت تغییرات شار مغناطیسی عبوری از مسیر فرضی برابر است با:

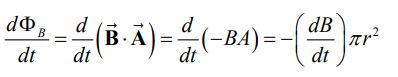
با استفاده از رابطه ۳ انتگرال میدان روی مسیر بسته فرض شده برابر است با:

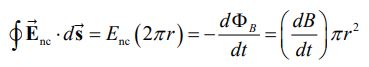
که رابطه زیر را نتیجه می‌دهد.

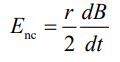
به طریقی مشابه برای حالت r>R، میدان القاء شده را می‌توان به‌ترتیب زیر بدست آورد.

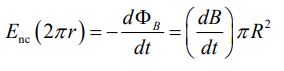
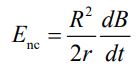
نمودار زیر میدان الکتریکی E_nc را بر حسب فاصله r نشان می‌دهد.

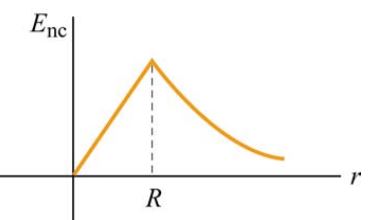
ژنراتورها

یکی از کاربرد‌های مهم قانون القای فارادی، در ژنراتور‌ها و موتور‌های الکتریکی است. یک ژنراتور به دستگاهی اطلاق می‌شود که در آن انرژی مکانیکی به انرژی الکتریکی تبدیل می‌شود؛ موتور الکتریکی، عکس ژنراتور عمل می‌کند و در واقع کار آن تبدیل انرژی الکتریکی به انرژی مکانیکی است. در شکل زیر نمای یک ژنراتور و موتور نشان داده شده است.

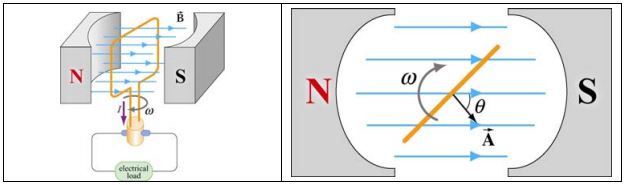
شکل سمت راست بالا، نمای یک ژنراتور را نشان می‌دهد. در آن از N حلقه استفاده شده که در میدان مغناطیسی دوران می‌کنند. با توجه به تعریف، شار عبوری از سطح این حلقه‌ها برابر است با:

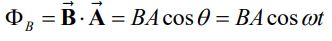
در نتیجه سرعت تغییرات شار مغناطیسی عبوری از حلقه را می‌توان مطابق با رابطه زیر محاسبه کرد.

با توجه به قانون القای فارادی نیروی محرکه القایی را به شکل زیر بدست می‌آوریم:

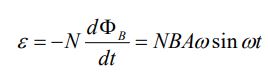
اگر حلقه را به مداری به مقاومت R متصل کنیم، جریان الکتریکی برابر با مقدار زیر بدست می‌آید.

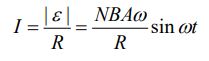
با توجه به مفاهیم بیان شده در مطلب جریان و مقاومت الکتریکی، توان خروجی ناشی از جریان القا شده برابر است با:

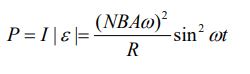
مقدار بالا توان الکتریکی بدست آمده از ژنراتور را نشان می‌دهد. حال می‌خواهیم توان ورودی به سیستم را محاسبه کنیم و مقدار آن را با توان خروجی بدست آمده در بالا مقایسه کنیم. بنابراین در ابتدا بایستی گشتاور مکانیکی وارد به حلقه محاسبه شود و سپس با استفاده از تعریف مکانیک کلاسیک از توان مصرفی جسم در حال دوران، توان ورودی را بدست آورد.

گشتاور وارد به حلقه با جریان I با استفاده از رابطه زیر محاسبه می‌شود.

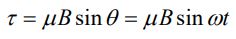
با استفاده از گشتاور وارد شده به حلقه، - از طرف میدان مغناطیسی - توان ورودی به حلقه به صورت زیر قابل محاسبه است.

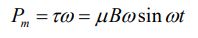
از طرفی گشتاور مغناطیسی برابر است با:

با جایگذاری عدد بالا در رابطه ۵ داریم:

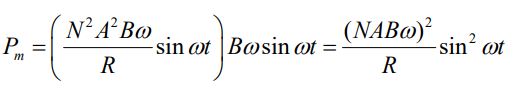
مقدار بالا برابر با رابطه ۴ است. در نتیجه مشاهده شد که توان ورودی و خروجی از ژنراتور با یکدیگر برابر است. در حقیقت قانون پایستگی انرژی برای این سیستم برقرار است.

قانون القای فارادی مبنای جریان‌هایی تحت عنوان، جریان متناوب هستند که در بخشی جداگانه به بررسی آن‌ها خواهیم پرداخت. البته جهت تسلط کامل به مبحث القای فارادی مثال‌هایی به صورت ویدئویی، در این آموزش حل شده که می‌توانند به شما کمک کنند.

چگونه مسائل را حل کنیم؟

در این مطلب قانون القای فارادی را معرفی کردیم و گفتیم که نیروی محرکه القا شده در نتیجه تغییر شار مغناطیسی، برابر با مقدار زیر است.

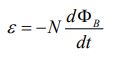
مطابق با این قانون، جریان القا شده در یک حلقه بسته برابر با I=|ε|/R است. در این رابطه R برابر با مقاومت حلقه در نظر گرفته می‌شود. به‌منظور محاسبه اندازه و جهت جریان القا شده، به ترتیب زیر عمل کنید:

1. برای یک سطح بسته با مساحت سطح A، بردار $$\overrightarrow{A}$$ را در یک جهت دلخواه در نظر بگیرید. این کار برای استفاده از قانون دست راست انجام می‌شود. پس از آن شار مغناطیسی را مطابق با روابط زیر بدست آورید:
   
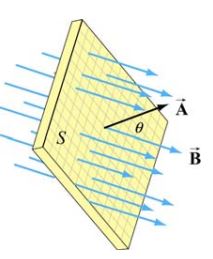
   توجه داشته باشید که پس از بدست آوردن Φ_B به علامت آن توجه کنید.
2. نرخ تغییراتِ میدان مغناطیسی یا همان dΦ_B/dt را محاسبه کنید. توجه داشته باشید که تغییرات شار نسبت به زمان می‌تواند در نتیجه تغییر یکی از عوامل زیر باشد:
   i. تغییرات میدان مغناطیسی غیر صفر باشد (۰≠dB/dt).
   ii. مساحت حلقه با زمان تغییر کند (۰≠dA/dt).
   iii. زاویه بین بردار میدان مغناطیسی و مساحت سطح حلقه با زمان تغییر کند (۰≠dθ/dt).
3. علامت نیرو محرکه القا شده (ε) را خلاف علامت تغییرات شار بدست آمده در نظر بگیرید.

مثال‌ها

جهت تسلط بیشتر به موضوع در این قسمت مثال‌هایی ارائه شده که پیشنهاد می‌شود، آن‌ها را به دقت مطالعه فرمایید.

مثال ۲: حلقه مستیطی در نزدیک سیم حامل جریان

مطابق با شکل زیر حلقه فلزی با عرض w و ارتفاع L را در نظر بگیرید که در فاصله s از سیمی قرار گرفته که جریان I را در خود حمل می‌کند.

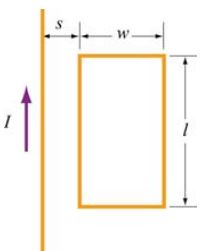
با توجه به مسئله توصیف شده، موارد زیر مطلوب است.

1. شار مغناطیسی عبوری از حلقه بسته
2. با فرض این‌که جریان مطابق با رابطه I=a+bt با زمان تغییر کند، نیروی محرکه القا شده و جهت جریان القایی را در حلقه بدست آورید.

(a): با استفاده از قانون آمپر می‌توان نوشت:

از طرفی سیم حامل جریان، میدانی مغناطیسی را در فاصله r از خود، برابر با مقدار زیر تولید می‌کند.

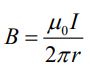
رابطه بالا نشان می‌دهد که میدان ناشی از سیم در جای‌جای حلقه متفاوت است. از این رو با فرض این‌که دیفرانسیل سطح برابر با dA=ldr باشد، شار مغناطیسی عبوری از سطح حلقه را می‌توان با انتگرال‌گیری از سمت چپ تا راست حلقه بدست آورد. بنابراین کل شار عبوری از سطح حلقه برابر است با:

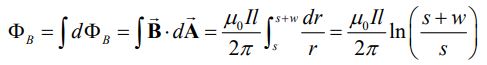
همان‌طور که مشخص شد، علامت شار بدست آمده مثبت است.

(b): با توجه به قانون القای فارادی، نیروی محرکه القا شده، برابر است با:

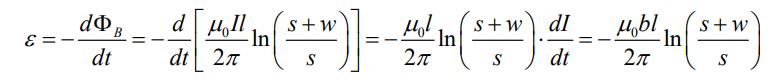
توجه داشته باشید که در رابطه بالا از رابطه زیر استفاده شده.

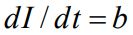
مثال ۳: تغییر مساحت حلقه با زمان

مطابق با شکل زیر، حلقه‌ای به شکل مربع را در نظر بگیرید که در میدان مغناطیسی درونسو و یکنواخت قرار گرفته است.

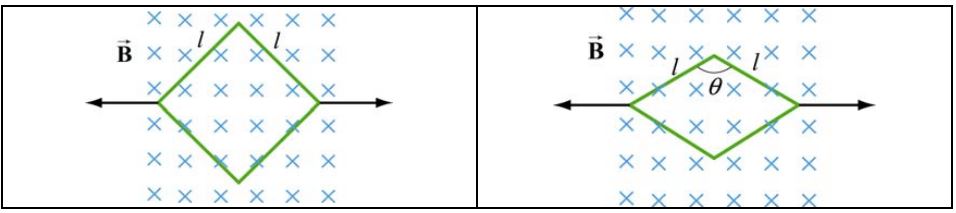
در بازه زمانی Δt، حلقه از دو سمت کشیده شده و به شکل لوزی در خواهد آمد. با فرض این‌که مقاومت کل حلقه برابر با R باشد، جریان الکتریکی القا شده در آن را بیابید.

با استفاده از قانون القای فارادی داریم:

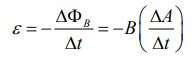
با توجه به شکل ارائه شده در صورت مثال، مساحت‌های اولیه و نهایی حلقه به ترتیب برابر با A_i=l² و A_f=l²sinθ هستند [توجه داشته باشید که مساحت لوزی مفروض برابر با اندازه ضرب خارجی $$|\overrightarrow{l_1}×\overrightarrow{l_2}|$$ است]. در نتیجه میانگین تغییرات مساحت در زمان برابر است با:

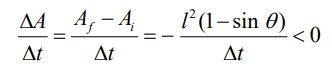
از این رو با استفاده از قانون القای فارادی داریم:

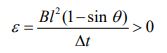
با بدست آمدن نیرو محرکه القایی، جریان القا شده در حلقه را نیز می‌توان با استفاده از قانون اُهم، به شکل زیر بدست آورد.

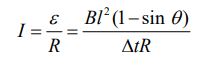
با توجه به این‌که تغییرات مساحت با زمان، منفی است در نتیجه شار مغناطیسی عبوری از حلقه نیز کاهش می‌یابد. بنابراین جریان در حلقه به صورتی حرکت خواهد کرد که شار مغناطیسی بدست آورده را تقویت کند. در نتیجه با استفاده از قانون دست راست، جهت جریان به صورت ساعتگرد بدست می‌آید.

مثال ۴: میله لغزنده

میله‌ای رسانا به طول L مطابق شکل زیر می‌تواند آزادانه روی دو رسانای دیگر بلغزد.

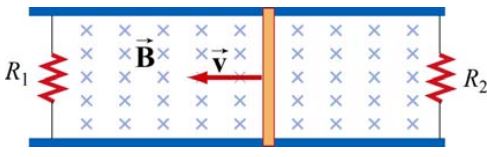
فرض کنید با استفاده از دو مقاومت R₁ و R₂ مداری بسته را ساخته‌ایم. تصور کنید که میدان مغناطیسی مفروض یکنواخت و جهت آن به سمت درون صفحه است. اگر با نیرویی خارجی، لغزنده را با سرعت ثابت به سمت چپ حرکت دهیم، موارد زیر مطلوب است:

1. جریانِ هرکدام از مقاومت‌ها
2. توان منتقل شده به مقاومت‌ها
3. نیروی مورد نیاز برای حرکت لغزنده

(a): نیرو محرکه القا شده بین دو انتهای لغزنده برابر است با:

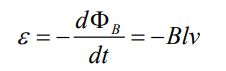
نیرو محرکه بدست آمده برابر با ولتاژ دو سر هر دو مقاومت است. در نتیجه جریان موجود در آن‌‌ها برابر هستند با:

از آنجایی که شار مغناطیسی موجود در حلقه سمت چپ با گذشت زمان کاهش می‌یابد، بنابراین جریان I₁ به صورت ساعتگرد در آن ایجاد می‌شود، تا شار درون صفحه را افزایش دهد. هم‌چنین شار عبوری از حلقه سمت راست در حال افزایش است، در نتیجه جریان I₂ به صورت پادساعتگرد خواهد بود.

(b): کل انرژی تلف شده در مقاومت‌ها برابر با حاصل جمع توان تلف شده در هرکدام از آن‌ها است. در حقیقت بایستی گفت:

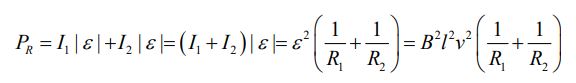
(c):‌ کل جریان عبوری از میله را می‌توان با استفاده از قانون گره، به شکل زیر بدست آورد.

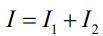
در نتیجه نیروی وارد به میله برابر است با:

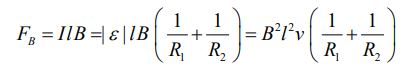
از آنجایی که حرکت میله با سرعت ثابت فرض شده، بایستی نیرویی برابر با F_B و به سمت راست، به میله وارد کرد. در حقیقت اگر نیروی خارجی وارد شده به میله را با F_ext نشان دهیم، خواهیم داشت:

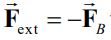
در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک و مهندسی برق، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی برق
• مجموعه آموزش‌های دروس فیزیک
• مجموعه آموزشی نرم‌ افزارهای برق و الکترونیک
• میدان مغناطیسی چیست؟ — به زبان ساده
• جریان و مقاومت الکتریکی — از صفر تا صد
• مدار الکتریکی — از صفر تا صد
• آهنربای الکتریکی – به زبان ساده