نیروی الکتریکی چیست؟ — به زبان ساده و با مثال

مطالعه ما در مورد الکتریسیته با الکترواستاتیک و نیروی الکتریکی یا الکترواستاتیک، یکی از چهار نیروی اساسی طبیعت آغاز می‌شود. نیروی الکتریکی یا الکترواستاتیک توسط قانون کولن توصیف می‌شود. از قانون کولن برای حل نیروهای ایجاد شده توسط پیکربندی بار استفاده می‌شود. در حقیقت الکترواستاتیک با نیروهای بین بارها سروکار دارد. استاتیک به این معنی است که بارها حرکت نمی‌کنند یا حداقل خیلی سریع حرکت نمی‌کنند. نیروی الکتریکی یک نیروی غیر تماسی است که در این مطلب در مورد آن صحبت خواهیم کرد.

نیرو چیست؟

نیرو کشیدن یا هل دادن یک جسم که دارای نماد $$F$$ است و واحد آن $$N$$ یا $$\frac{kg.m}{s^2}$$ است. در حقیقت نیرو به هر تأثیری گفته می‌شود که باعث تغییر یک جسم، چه در مورد حرکت، جهت یا ساختار هندسی آن شود. به بیان دیگر در فیزیک، نیرو به هر تأثیری گفته می‌شود که باعث می‌شود یک جسم دچار تغییر خاصی شود، چه در مورد حرکت، جهت یا ساختار هندسی آن. کمیت نیرو به افتخار ایزاک نیوتن با واحد SI نیوتن اندازه گیری می‌شود.

نیرو کمیتی است که می‌تواند باعث شود جسمی که دارای جرم است سرعت خود را تغییر دهد، یعنی شتاب بگیرد، یا باعث تغییر شکل جسمِ انعطاف پذیر شود. نیرو را می‌توان با مفاهیم شهودی مانند فشار یا کشیدن نیز توصیف کرد. یک نیرو هم قدر و هم جهت دارد و به همین دلیل آن را کمیت برداری می‌نامند. برای آشنایی بیشتر با مفهوم نیرو مطلب «نیرو چیست و با چه واحدی اندازه گیری می شود؟ — به زبان ساده» را مطالعه کنید.

نیروی غیرتماسی چیست؟

نیروهای غیر تماسی نیروهایی هستند که بدون تماس بین دو جسم اعمال می‌شوند و به سه دسته کلی تقسیم بندی می‌شوند که عبارتند از:

• نیروی گرانش
• نیروی الکترومغناطیسی (نیروی الکتریکی + نیروی مغناطیسی)
• نیروی هسته ای

در این مطلب با جزئیات بیشتری نیروی غیر تماسی الکتریکی را بررسی می‌کنیم، اما برای مطالعه بیشتر در مورد نیروی غیر تماسی مطلب «نیروی غیر تماسی چیست؟ — به زبان ساده و با مثال» را مطالعه کنید.

نیروی الکتریکی چیست؟

برهم کنش جاذبه یا دافعه بین هر دو جسم باردار یک نیروی الکتریکی است. مانند هر نیرویی، تأثیر این نیرو نیز بر اجسام با قوانین حرکت نیوتن توصیف می‌شود. نیروی الکتریکی یعنی به $$F_{elect}$$ به لیست طولانی نیروهای دیگری می‌پیوندد که می‌توانند بر روی اجسام عمل کنند.

قوانین نیوتن برای تجزیه و تحلیل حرکت (یا عدم حرکت) اجسام تحت تأثیر یک یا ترکیبی از نیروها بررسی می‌شود. در این حالت تجزیه و تحلیل معمولاً با رسم یک نمودار آزاد جسم آغاز می‌شود که در آن نوع و جهت نیروهای منفرد با فلش‌های برداری نشان داده شده و بر اساس نوع برچسب گذاری می‌شوند. سپس بزرگی نیروها به عنوان اندازه بردار در نظر گرفته می‌شود تا مجموع حاصل یا نیروی برآیند که به عنوان نیروی خالص نیز شناخته می‌شود، تعیین شود. در نهایت از نیروی برآیند می‌توان برای تعیین شتاب جسم استفاده کرد.

در برخی موارد، هدف تجزیه و تحلیل، تعیین شتاب جسم نیست. در عوض، نمودار جسم آزاد برای تعیین جدایی یا بار دو جسمی که در تعادل ایستا هستند استفاده می‌شود. در این مورد، نمودار جسم آزاد با درک اصول بردار ترکیب می‌شود تا مقداری ناشناخته در یک مسئله که شامل هندسه، مثلثات و قانون کولن است، تعیین شود. در این مطلب هر دو نوع کاربرد قوانین نیوتن در پدیده الکتریسیته ساکن را بررسی خواهیم کرد.

بار الکتریکی چیست؟

چگونه بفهمیم چیزی به نام بار الکتریکی یا شارژ وجود دارد؟ مفهوم بار از مشاهده طبیعت ناشی می‌شود زیرا که ما به عنوان ناظر نیروهایی را بین اجسام مشاهده می‌کنیم. بار الکتریکی خاصیت اجسام است که این نیروی مشاهده شده را ایجاد می‌کنند. مانند گرانش، نیروی الکتریکی نیز یک نیروی غیر تماسی است.

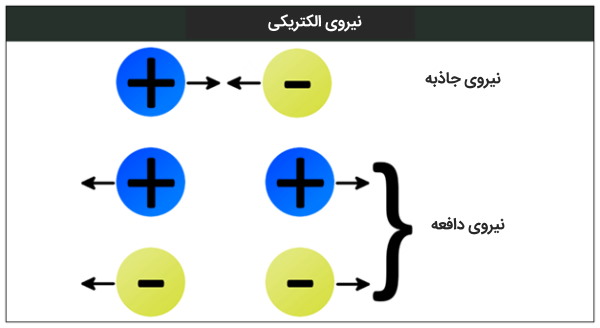
این ایده که یک نیرو می‌تواند در فاصله و بدون تماس عمل کند بسیار شگفت انگیز است، اما این چیزی است که در طبیعت واقعاً اتفاق می‌افتد. نیروی الکتریکی بسیار بزرگتر از نیروی گرانش است. بر خلاف گرانش، دو نوع بار الکتریکی وجود دارد در حالی که تنها یک نوع گرانش وجود دارد. در حقیقت نیروی گرانشی فقط از نوع جاذبه است. در نیروی الکتریکی بارهای غیر همنام یکدیگر را جذب می‌کنند در حالی که بارهای همنام یکدیگر را دفع می کنند. این موضوع در شکل زیر نمایش داده شده است:

برای آشنایی بیشتر با مفهوم بار الکتریکی و کوانتیدگی بار الکتریکی مطلب «پایستگی و کوانتیده بودن بار الکتریکی | به زبان ساده» را مطالعه کنید.

نیروی بین بارهای الکتریکی: قانون کولن برای نیروی الکتریکی

قانون کولن به خوبی چیزی را که در طبیعت مشاهده می‌کنیم توضیح می‌دهد. در حقیقت داریم:

$$\large \overrightarrow{F}=K\frac{q_0 q_1}{r^2}\hat{r}$$

در این معادله $$\overrightarrow{F}$$ نیروی الکتریکی است که به صورت بردار بین دو بار الکتریکی یا دو جسم باردار قرار می‌گیرد. $$K$$ ثابت الکتریکی است که قسمت چپ معادله که بر حسب نیوتن است را به سمت راست معادله که بر حسب کولن و متر است را به هم مرتبط می‌کند. این ثابت نیاز است تا جوابی که از معادله به دست می‌آید با تجربه ما از طبیعت همخوانی داشته باشد.

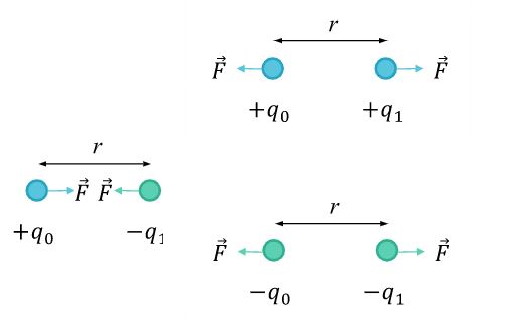
$$q_0$$ و $$q_1$$ مقدار بار الکتریکی در هر جسم را بر حسب کولن نشان می‌دهند. کولن واحد بار الکتریکی در سیستم اندازه گیری SI است. $$r$$ فاصله بین اجسام باردار است و $$\hat{r}$$ بردار یکه است که جهت بردار نیروی بین دو جسم باردار را نشان می‌دهد. همان طور که گفتیم این نیرو برای دو جسم با بار الکتریکی یکسان دافعه و برای دو جسم با بار الکتریکی غیر یکسان جاذبه است.

ثابت الکتریکی یا ضریب گذردهی فضای آزاد $$\large\epsilon_0$$

K، ثابت تناسب است که اغلب به شکل زیر ظاهر می‌شود و داریم:

$$\large K=\frac{1}{4 \pi \epsilon_0}$$

این ثابت مربوط به قضیه شار گاوس است. در این شکل نوشتار از ثابت می‌توان متوجه شد که ثابت K حاوی یک عامل هندسی و عامل دیگری است که توسط مشاهدات تجربی به دست می‌آید. قضیه گاوس مساحت یک کره را در بر می‌گیرد. ضریب هندسی $$4\pi$$ زاویه ثابت یک کره است (مشابه با زاویه کل $$2\pi$$ برای یک دایره). بقیه ثابت تناسب نشان‌دهنده چیزی است که تنظیمات تجربی به ما می‌دهد و در $$\epsilon_0$$ گنجانده شده است. این نماد به بیان ساده‌ای از قانون گاوس منجر می‌شود. بدین ترتیب می‌توان قانون کولن را به شکل زیر نوشت:

$$\large \overrightarrow{F}=\frac{1}{4\pi \epsilon_0}\frac{q_0 q_1}{r^2}\hat{r}$$

حرف یونانی $$\epsilon_0$$ ثابت الکتریکی است که به عنوان ثابت گذردهی فضای آزاد نیز شناخته می‌شود که منظور از فضای آزاد خلاء است. قانون کولن چیزی را که در طبیعت رخ می‌دهد را توضیح می‌دهد. ثابت الکتریکی $$\epsilon_0$$ تنظیمات آزمایشگاهی و سیستم واحدها را نیز شامل می‌شود. منظور از شرایط آزمایشگاهی، حالتی است که در آن $$\overrightarrow{F}$$ را برای یک بار نقطه‌ای یا هر چیزی که شبیه به یک بار نقطه‌ای مانند یک کره باردار رفتار می‌کند، اندازه گیری می‌کنیم. در سیستم SI، $$\epsilon_0$$ به صورت تجربی دارای مقدار زیر است:

$$\epsilon_{0}=8.854187817 \times 10^{-12} \text { coulomb }^{2} / \text { newton-meter }^{2}$$

این مقدار $$\epsilon_0$$ باعث می‌شود ثابت K دارای مقدار زیر شود:

$$K=\frac{1}{4 \pi \epsilon_{0}}=\frac{1}{4 \pi \cdot 8.854 \times 10^{-12}}=8.987 \times 10^{9}$$

که معمولاً برای حل مسائل مهندسی این مقدار را گرد می‌کنیم و داریم:

$$\large K=\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9}$$

دیمانسیون K نیز برابر با نیوتن در متر مربع بر مجذور کولن است.

سه بار نقطه‌ای

برای بررسی بیشتر، می‌خواهیم با استفاده از قانون کولن نیروی وارد بر دو بار اطراف یک بار سوم را محاسبه کنیم. سه بار الکتریکی را در سه راس مثلث با زاویه‌های $$30^{\circ}$$، $$60^{\circ}$$ و $$90^{\circ}$$ در نظر می‌گیریم. بار آزمایشی که می‌خواهیم نیروی الکتریکی را بر روی آن محاسبه کنیم بار الکتریکی $$q_2$$ است.

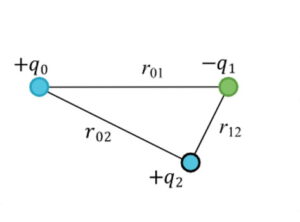
اگر بار الکتریکی برای بار $$q_0$$، $$q_1$$ و $$q_2$$ به ترتیب $$+4, -1$$ و $$+3$$ کولن باشد و فاصله بین بارها به صورت زیر باشد، داریم:

برای محاسبه نیروی الکتریکی طبق قانون کولن باید بارهای الکتریکی را به صورت جفت در نظر بگیریم. در این مثال جفت بار الکتریکی عبارت از $$q_0, q_2$$ و $$q_1, q_2$$ هستند. بردارهای نیرو در خط اتصال بین جفت بارها  به صورت زیر هستند:

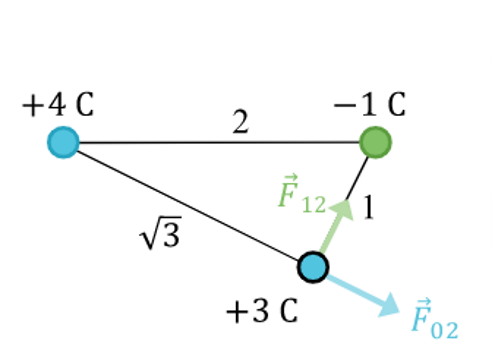
برای سادگی محاسبات $$K$$ را به صورت نماد استفاده می‌کنیم و از مقدار عددی آن استفاده نمی‌کنیم. بدین ترتیب مقدار نیروها برابر هستند با:

$$\large F=K\frac{q_0 q_1}{r^2}$$

در نتیجه نیروی $$F_{02}$$، یعنی نیروی بین بار $$q_0$$ و $$q_2$$ برابر است با:

$$\large F_{02}=K\frac{4 \times 3}{(\sqrt{3})^2}=4K$$
$$\large F_{12}=K\frac{1 \times 3}{(1)^2}=3K$$

مرحله بعد این است که نیروی الکتریکی برآیند را محاسبه کنیم. همان طور که گفتیم نیرو یک کمیت برداری است که دارای اندازه و جهت است. بنابراین با استفاده از جمع برداری می‌توانیم برآیند و جهت دو بردار $$F_{02}$$ و $$F_{12}$$ را محاسبه کنیم. بدین ترتیب داریم:

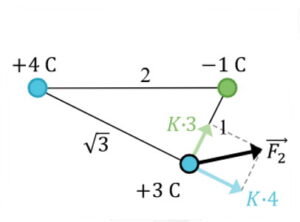
با استفاده از قضیه فیثاغورس برآیند دو بردار برابر است با:

$$\large \left|F_{2}\right|=K \cdot \sqrt{3^{2}+4^{2}}=K \cdot 5$$

برای محاسبه زاویه بردار نیروی برآیند یعنی $$F_2$$ با راستای افقی، با توجه به اندازه بردارها و روابط مثلثاتی داریم:

$$\large arc \sin(4/5)=53.13^{\circ}$$

$$\large arc \sin(3/5)=36.86^{\circ}$$

تصویر مثلث حاصل از سه بردار $$3K$$، $$4K$$ و $$5K$$ به صورت زیر خواهد بود:

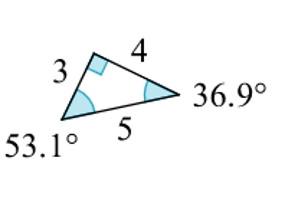
توزیع بار به صورت خطی

مثال بعدی که در استفاده از قانون کولن برای محاسبه نیروی الکتریکی مورد استفاده قرار می‌دهیم به شکل زیر است:

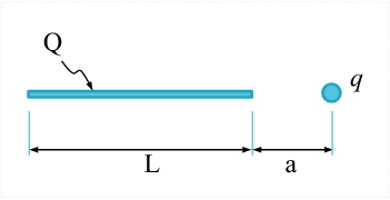
یک خط بار به طول L دارای بار کل $$Q$$ است. فرض کنید بار $$Q$$ به طور یکنواخت در طول $$L$$ پراکنده شده است. همچنین یک بار نقطه‌ای $$q$$ به فاصله $$a$ از انتهای میله قرار گرفته است. نیروی کل وارد بر بار q که در انتهای میله قرار گرفته است چه قدر است؟

خط بار شامل بار کل $$Q$$ است. برای حل این مسئله می‌توان خط بار را به صورت تعداد زیادی بار نقطه‌ای در نظر گرفت که مجموع بار آن‌ها Q است و پهلو به پهلوی هم قرار گرفته‌اند. برای محاسبه نیروی وارد بر بار q، باید مجموع (انتگرال) نیروهای هر بار نقطه‌ای در خط بار را به دست آوریم. چگالی بار خطی به این ترتیب برابر با $$\frac{Q}{L}$$ کولن بر متر خواهد بود و بدین ترتیب می‌توان جزء بار را در هر تکه از خط بار یعنی $$dx$$ به دست آورد. بدین ترتیب داریم:

$$\large dQ=\frac{Q}{L} dx$$

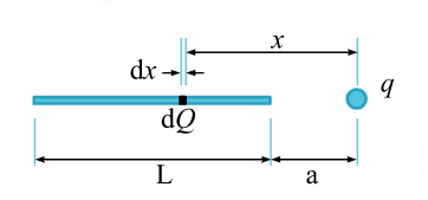
$$dQ$$ بسیار نزدیک به یک بار نقطه‌ای عمل می‌کند و این موضوع به ما اجازه می‌دهد تا از قانون کولن استفاده کنیم. جهت نیروی الکتریکی حاصل نیز خط واصل بین بار نقطه‌ای و $$dQ$$ قرار دارد. بدین ترتیب اندازه هر جزء نیرو برابر است با:

$$dF=\frac{1}{4\pi \epsilon_0} \frac{q dQ}{x^2}$$

که در این رابطه $$x$$ فاصله بین بار نقطه‌ای و هر جزء بار پیوسته است. برای به دست آوردن نیروی کل باید هر جزء از نیروها را به دست آوریم و با یکدیگر جمع کنیم. این مجموع باید در فاصله بین $$a+L$$ تا $$a$$ در نظر گرفته شود. بدین ترتیب داریم:

$$\large F=\int_{a}^{a+L} \mathrm{~d} \vec{F}=\int_{a}^{a+L} \frac{1}{4 \pi \epsilon_{0}} \frac{q \mathrm{~d} Q}{x^{2}}$$

این معادله $$x$$ و $$dQ$$ را به عنوان متغیر مستقل خواهد داشت. برای رسیدن به یک متغیر مستقل، $$dQ$$ را با عبارت $$\frac{Q}{L} dx$$ از بالا جایگزین می‌کنیم و بدین ترتیب داریم:

$$\large F=\int_{a}^{a+L} \frac{1}{4 \pi \epsilon_{0}} \frac{q Q}{L} \frac{1}{x^{2}} \mathrm{~d} x$$

همه مقادیر ثابت را از انتگرال بیرون می‌آوریم و بدین ترتیب داریم:

$$\large F=\frac{1}{4 \pi \epsilon_{0}} \frac{q Q}{L} \int_{a}^{a+L} \frac{1}{x^{2}} \mathrm{~d} x$$

با حل انتگرال و در نظر گرفتن حدود انتگرال، در نهایت نیروی وارد بر بار نقطه‌ای به صورت زیر محاسبه می‌شود و برابر است با:

$$\large F=\frac{1}{4 \pi \epsilon_{0}}\frac{qQ}{a(a+L)}$$

در ارتباط با این جواب چند نکته وجود دارد که باید آن‌ها را بیان کرد:

• صورت این جواب برابر با حاصلضرب اندازه بار نقطه‌ای و بار روی میله است که از لحاظ منطقی با آن‌ چه از قانون کولن می‌دانیم توافق دارد.
• مخرج کسر که در قانون کولن برابر با فاصله به توان دو است به صورت $$a$$ در $$a+L$$ آمده است، که از هندسه خاص این مسئله ناشی می‌شود.
• اگر بار نقطه‌ای $$q$$ را به فاصله خیلی دورتر از $$L$$ منتقل کنیم، بار خطی روی میله $$L$$ شبیه به یک بار نقطه‌ای رفتار می‌کند و مخرج تبدیل به $$a^2$$ می‌شود. بنابراین در فاصله‌های زیاد، خط بار تبدیل به یک کره باردار با بار نقطه‌ای Q می‌شود و جواب به دست آمده تبدیل به قانون کولن می‌شود.

به صورت کلی باید گفت قانون کولن انتخاب خوبی برای موقعیت‌هایی با بارهای نقطه‌ای و یا هندسه‌های متقارن ساده مانند خطوط یا کره‌های بار است. از آنجایی که قانون کولن بر پایه نیروهای زوجی بین بارها استوار است، وقتی با بارهای چندگانه یعنی بیش از دو بار نقطه‌ای مواجه می‌شویم، نیروهای بین هر جفت بار را محاسبه می‌کنیم و سپس بردار نیروی الکتریکی برآیند را محاسبه خواهیم کرد. همچنین برای موقعیتی که در آن بار به صورت توزیع شده است، به طور خلاقانه چگالی بار توزیع شده را به عنوان مجموعه‌ای از بارهای نقطه‌ای مدل کرده و نیروی برآیند را محاسبه می‌کنیم.

در این حالت $$dQ$$ نشان دهنده یک توزیع بار بی نهایت کوچک در فضای توزیع بار مورد بحث در مسئله است. بدین ترتیب نیروی الکتریکی بین بار نقطه‌ای و هر جزء بار کوچک توزیع شده را محاسبه می‌کنیم. مجموع این نیروها را توسط انتگرال به دست می‌آوریم. این انتگرال بردار برآیند نیروی الکتریکی وارد بر بار الکتریکی نقطه‌ای است.

نیروی الکتریکی و شتاب

فرض کنید که یک بادکنک و یک لوله گلف پلاستیکی که هر دو با مالیدن به پارچه‌های پشمی دارای بار منفی می‌شوند، وجود دارد. فرض کنید که بادکنک به هوا فرستاده می‌شود و لوله گلف در زیر آن نگه داشته می‌شود تا بادکنک را در هوا معلق نگه کند. این هدف زمانی محقق می‌شود که جداسازی فضایی بین اجسام باردار به گونه‌ای تنظیم شود که نیروی گرانش رو به پایین ($$F_{grav}$$) و نیروی الکتریکی رو به بالا ($$F_{elect}$$) با یکدیگر در حال تعادل قرار داشته باشند.

این کار نسبتاً دشوار است زیرا بادکنک دائماً تحت تأثیر نیروی گرانش و نیروی الکتریکی از یک سمت به سمت دیگر و همچنین به سمت بالا و پایین حرکت می‌کند. وقتی لوله گلف خیلی دور از بادکنک نگه داشته شود، بادکنک می‌افتد و به سمت پایین شتاب می‌گیرد. این اتفاق به نوبه خود فاصله جداسازی بین بادکنک و لوله گلف را کاهش می‌دهد و منجر به افزایش نیروی الکتریکی می‌شود. با افزایش $$F_{elect}$$، مقدار آن از $$F_{grav}$$ بیشتر می‌شود و بالون ناگهان به سمت بالا شتاب می‌گیرد.

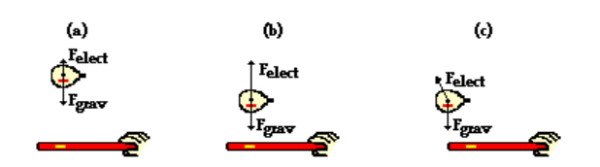
همچنین اگر نقطه بار روی لوله پلاستیکی مستقیماً زیر نقطه بار بادکنک نباشد که این موضوع یک سناریوی کاملاً محتمل است، نیروی الکتریکی با زاویه‌ای نسبت به جهت عمودی وارد می‌شود و بادکنک شتاب جانبی خواهد داشت. نتیجه محتمل چنین تلاشی برای معلق کردن بالون، انواع شتاب‌های لحظه‌ای در جهات مختلف خواهد بود. فرض کنید در یک لحظه در روند تلاش برای معلق کردن بالون، شرایط زیر به وجود آید:

یک بادکنک $$0.9$$ گرمی با بار الکتریکی $$75$$ نانوکولن در فاصله 12 سانتی متری بالای لوله گلف پلاستیکی قرار دارد که دارای بار الکتریکی $$83$$ نانوکولن است. چگونه می‌توان قوانین نیوتن را برای تعیین شتاب بالون در این لحظه اعمال کرد؟

مانند هر مسئله‌ای که شامل نیرو و شتاب است، حل این حالت با رسم نمودار آزاد جسم آغاز می‌شود. دو نیرو بر روی بالون عمل می‌کنند. نیروی گرانش روی بادکنک به سمت پایین و نیروی الکتریکی به سمت بالا اعمال می‌شود زیرا بادکنک و لوله گلف دارای بار الکتریکی هستند و لوله گلف در زیر بادکنک نگه داشته می‌شود. این دو نیرو در نمودار آزاد جسم در شکل زیر نشان داده شده‌اند. مرحله دوم شامل تعیین بزرگی این دو نیرو است. نیروی گرانش با ضرب جرم (به کیلوگرم) در شتاب گرانش تعیین می‌شود.

$$$$\large \begin{aligned}
F_{\text {grav }}=& m . g=(0.00090 \mathrm{~kg}) .(9.8 \mathrm{~m} / \mathrm{s^2}) \\
& F_{\text {grav }}=8.82 \times 10^{-3} \mathrm{~N}
\end{aligned}$$$$

جهت نیروی گرانشی به سمت پایین است. نیروی الکتریکی نیز با استفاده از قانون کولن تعیین می‌شود. واحد بار الکتریکی کولن (C) و واحد فاصله جدایی بین بارهای الکتریکی بر حسب متر (m) است. استفاده از این واحدها منجر به یک واحد نیروی نیوتن می شود. بدین ترتیب نیروی الکتریکی نیز برابر است با:

$$\large \begin{aligned}
F_{\text {elect }} &=k \cdot Q_{1} \cdot Q_{2} / d^{2} \\
F_{\text {elect }}=\left(9 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / C^{2}\right) & .\left(-75 \times 10^{-9} \mathrm{C}\right) \cdot\left(-83 \times 10^{-9} \mathrm{C}\right) /(0.12)^{2} \\
F_{\text {elect }} &=3.89 \times 10^{-3} \mathrm{~N}
\end{aligned}$$

نیروی برآیند یا نیروی کل حاصل جمع برداری این دو نیرو است. نیروهای رو به بالا و پایین به عنوان بردار با هم جمع می‌شوند و داریم:

$$\large \begin{gathered}
\mathrm{F}_{\text {net }}=\mathrm{F}_{\text {grav }} \text { (down) }+\mathrm{F}_{\text {elect }}(\text { up }) \\
\mathrm{F}_{\text {net }}=8.82 \times 10^{-3} \mathrm{~N}, \text { down }+3.89 \times 10^{-3} \mathrm{~N}, \text { up } \\
\mathrm{F}_{\text {net }}=4.93 \times 10^{-3} \mathrm{~N}
\end{gathered}$$

همان طور که مشخص است، جهت این نیرو به سمت پایین است. مرحله آخر این مسئله شامل استفاده از قانون دوم نیوتن برای تعیین شتاب جسم است. بر اساس قانون دوم نیوتن شتاب برابر با نیروی خالص تقسیم بر جرم (به کیلوگرم) است و داریم:

$$\large \begin{gathered}
\mathrm{a}=\mathrm{F}_{\text {net }} / \mathrm{m}=\left(4.93 \times 10^{-3} \mathrm{~N}, \text { down }\right) /(0.00090 \mathrm{~kg}) \\
\mathrm{a}=5.5 \mathrm{~m} / \mathrm{s^2}
\end{gathered}$$

جهت شتاب حرکت نیز هم راستا با جهت حرکت است. تجزیه و تحلیل بالا نشان می‌دهد که چگونه قانون دوم نیوتن و قانون کولن را می‌توان برای تعیین شتاب لحظه‌ای به کار برد. تحلیل بعدی شامل حالتی است که در آن دو جسم در حالت تعادل ساکن هستند.

نیروی الکتریکی و تعادل استاتیک

فرض کنید دو بادکنک با دو نخ بلند از سقف به صورت عمودی آویزان شده‌اند. هر بادکنک را ده بار با پارچه پشمی مالش داده‌ایم. بادکنک‌ها که نسبت به پارچه پشمی جاذبه بیشتری برای الکترون دارند، بار منفی به دست می‌آورند. بادکنک‌ها دارای یک نوع بار الکتریکی خواهند بود و متعاقباً یکدیگر را دفع می‌کنند. نتیجه دفع آن‌ها این است که نخ‌ها و بادکنک‌های معلق اکنون با راستای عمود زاویه ایجاد می‌کنند. زاویه ریسمان با راستای عمود از نظر ریاضی با مقدار بار روی بادکنک‌ها مرتبط است.

همان طور که بالن‌ها مقدار بیشتری بار بدست می‌آورند، نیروی دافعه بین آن‌ها افزایش می‌یابد و زاویه‌ای که نخ با راستای عمود ایجاد می‌کند نیز افزایش می‌یابد. مانند هر موقعیتی که شامل نیروی الکترواستاتیکی است، این وضعیت را می‌توان با استفاده از اصول برداری و قوانین نیوتن تحلیل کرد.

فرض کنید شرایط زیر وجود داشته باشد. دو بادکنک $$1/1$$ گرمی از رشته‌های نخ ۲ متری آویزان شده و از سقف آویزان شده‌اند. سپس بادکنک‌ها ده بار با پارچه پشمی مالش داده می‌شوند تا یک بار Q یکسان به هر بادکنک القا شود. بادکنک‌ها یکدیگر را دفع می‌کنند و هر رشته با راستای عمودی زاویه 15 درجه ایجاد می‌کند. در این حالت می‌خواهیم نیروی دافعه الکتریکی، بار روی هر بادکنک (که فرض می‌شود یکسان است) و مقدار الکترون‌های منتقل شده به هر بادکنک که در نتیجه 10 بار مالش با پارچه پشمی ایجاد شده است را تعیین کنیم.

به دلیل پیچیدگی موقعیت فیزیکی، عاقلانه است که آن را با استفاده از نمودار آزاد جسم نشان دهیم. نمودار به عنوان وسیله‌ای برای شناسایی اطلاعات شناخته شده برای این وضعیت عمل می‌کند. در این نمودار مانند شکل زیر،‌ دو بادکنک را با نخی به طول L و زاویه $$\theta$$ نشان داده‌ایم. جرم (m) بادکنک‌ها مشخص است که در اینجا به کیلوگرم (واحد استاندارد جرم) بیان می‌شود. فاصله بین بادکنک‌ها روی را با متغیر d نشان می‌دهیم.

خط عمودی از نقطه محوری یا پیوت روی سقف ترسیم شده است. این خط عمودی یک ضلع مثلث قائم الزاویه است که توسط خط افقی که بادکنک‌ها را به هم متصل می‌کند و رشته‌ای که از بالن تا سقف امتداد می‌یابد تشکیل شده است. این مثلث قائم الزاویه برای تحلیل موقعیت با استفاده از اصول برداری مفید خواهد بود. توجه داشته باشید که خط عمودی خطی را که بادکنک‌ها را به هم وصل می‌کند، نصف می‌کند و بنابراین، یک ضلع از مثلث قائم الزاویه دارای فاصله $$d/2$$ است.

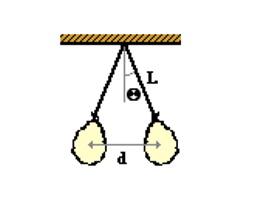
اعمال قوانین نیوتن در این موقعیت با ساختن نمودار آزاد جسم برای یکی از بادکنک‌ها آغاز می‌شود. سه نیرو بر روی بادکنک‌ها اثر می‌گذارد که عبارت از نیروی کشش نخ، نیروی گرانش و نیروی الکترواستاتیک دافعه هستند. این سه نیرو برای بادکنک سمت راست در شکل زیر نشان داده شده‌اند. توجه داشته باشید که نیروی کشش در زاویه‌ای نسبت به خط عمود قرار می‌گیرند. در فیزیک، چنین موقعیت‌هایی با تفکیک بردار نیرو به اجزای افقی و عمودی بررسی می‌شوند. این موضوع در شکل زیر نشان داده شده و بردارها به صورت مولفه‌های $$F_x$$ و $$F_y$$ نمایش داده شده‌اند. این مولفه‌ها با توابع مثلثاتی و با زاویه‌ای که در راستای عمود ایجاد می‌شوند، ارتباط دارند. از آنجایی که بادکنک‌ها در حالت تعادل هستند، نیروهایی که بر بادکنک‌ها وارد می‌شوند باید یکدیگر را خنثی کنند. این بدان معنا است که جزء عمودی نیروی کشش ($$F_y$$) باید نیروی گرانش رو به پایین یعنی $$F_{grav}$$ را خنثی کند و جزء افقی نیروی کشش ($$F_x$$) باید نیروی الکترواستاتیکی که به سمت راست وارد می‌شود ($$F_{elect}$$) را خنثی کند.

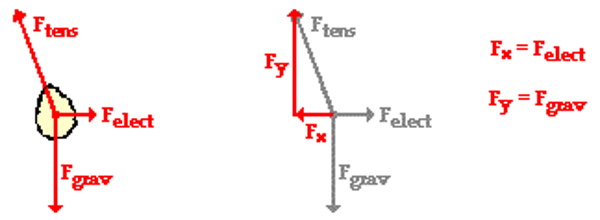
از آنجایی که جرم بادکنک مشخص است، می‌توان نیروی گرانش وارد بر بادکنک را تعیین کرد.

$$\large \begin{gathered}
\mathrm{F}_{\text {grav }}=\mathrm{m} . \mathrm{g}=(0.0011 \mathrm{~kg}) \cdot(9.8 \mathrm{~m} / \mathrm{s^2}) \\
\mathrm{F}_{\text {grav }}=0.01078 \mathrm{~N}
\end{gathered}$$

نیروی گرانش برابر با مولفه عمودی نیروی کشش است ($$\large F_y=0.0108\ N$$). مولفه $$F_y$$ با مولفه $$F_x$$ و زاویه تتا با تابع مماس مرتبط است. از این رابطه می‌توان برای تعیین مولفه افقی نیروی کشش استفاده کرد. بدین ترتیب داریم:

$$\tan(\theta) = \mathrm{F}_{\mathrm{x}} / \mathrm{F}_{\mathrm{y}} \\
\tan(15^{\circ}) =\mathrm{F}_{\mathrm{x}} /(0.01078 \mathrm{~N}) \\
\Rightarrow \mathrm{F}_{\mathrm{x}}=(0.01078 \mathrm{~N}) \cdot \tan (15 ^{\circ}) \\
\mathrm{F}_{\mathrm{x}}=0.00289 \mathrm{~N}$$

مولفه افقی نیروی کشش برابر با نیروی الکترواستاتیک است و بدین ترتیب داریم:

$$F_{elect}=0.00289\ N$$

اکنون که نیروی الکترواستاتیک با استفاده از قوانین نیوتن و اصول برداری تعیین شده است، می‌توان از قانون کولن برای تعیین بار روی بادکنک استفاده کرد. فرض بر این است که بادکنک‌ها مقدار بار یکسانی دارند زیرا با 10 بار مالش باردار شده‌اند. از آنجا که بار دو بادکنک یکسان است یعنی $$Q_1=Q_2$$ است، می‌توان قانون کولن را به صورت زیر بازنویسی کرد و داریم:

$$\large F=\frac{k.Q^2}{d^2}$$

این معادله را می توان به صورت جبری به منظور به دست آوردن بار $$Q$$ مجدداً بازنویسی کرد و داریم:

$$\begin{gathered}
\mathrm{F} \cdot \mathrm{d}^{2}=\mathrm{k} \cdot \mathrm{Q}^{2} \\
\mathrm{Q}^{2}=\mathrm{F} \cdot \mathrm{d}^{2} / \mathrm{k} \\
\mathrm{Q}=\sqrt{\frac{F.d^2}{k}}
\end{gathered}$$

برای به دست آوردن مقدار بار الکتریکی روی بادکنک‌ها دانستن مقدار d یا فاصله بین بادکنک‌ها مهم است. بدین منظور باید از مثلث قائم الزاویه برای تعیین طول ضلع مقابل زاویه 15 درجه استفاده کرد. این طول نصف فاصله d است. بدین منظور داریم:

$$\begin{aligned}
&\sin(\theta) = opposite side / hypotenuse side \\
&\sin(15^{\circ})=\text {opposite side / }(2.0 \mathrm{~m}) \\
&\text { opposite side }=(2.0 \mathrm{~m}) . \sin(15^{\circ}) \\
&\text { opposite side }=\mathrm{d} / 2=0.518 \mathrm{~m}
\end{aligned}$$

با دوبرابر کردن این فاصله، مقدار d برابر با 1٫035 متر به دست می‌آید. بدین ترتیب با جایگزین کردن مقدار d در رابطه به دست آمده برای Q، مقدار بار الکتریکی به صورت زیر به دست می‌آید:

$$\begin{gathered}
\mathrm{Q}=\sqrt{\frac{F.d^2}{k}}\\
\mathrm{Q}=\sqrt{\frac{(0.00289 \mathrm{~N}). (1.035 \mathrm{~m})^{2}}{9 \times 10^{9} \mathrm{~N} . \mathrm{m}^{2} / \mathrm{C}^{2}}} \\
\mathrm{Q}=5.87 \times 10^{-7} \mathrm{C}(\text { negative })
\end{gathered}$$

بار روی یک جسم به تعداد الکترون‌های اضافی (یا کمبود الکترون) در جسم مربوط می‌شود. با استفاده از بار یک الکترون منفرد یعنی مقدار $$-1.6 \times 10^{-19}\ C$$، می‌توان تعداد الکترون‌های روی این جسم را تعیین کرد:

$$\begin{aligned}
&\text { excess electrons }=(-5.87 \times 10^{-7} \mathrm{C}) /\left(-1.6 \times 10^{-19} \mathrm{C} / \text { electron }\right) \\
&\quad \text { excess electrons }=3.67 \times 10^{12} \text { electrons }
\end{aligned}$$

بدین ترتیب در طول فرآیند باردار شدن، بیش از سه تریلیون الکترون از پارچه پشمی به هر یک از بادکنک‌ها منتقل شده است.

نیروی الکتریکی چه نوع نیرویی است؟

نیروی الکتریکی یک نیروی غیر تماسی است که بدون تماس دو جسم باردار اعمال می‌شود.

معرفی فیلم آموزش فیزیک پایه یازدهم فرادرس

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک یازدهم کرده است. این مجموعه آموزشی مباحث فیزیک یازدهم را پوشش می‌دهد. در این مجموعه ابتدا به آموزش الکتریسیته ساکن، میدان الکتریکی، خطوط میدان الکتریکی، انرژی پتانسیل الکتریکی، خازن و دی الکتریک پرداخته می‌شود و در انتهای بخش اول نمونه تست‌های کنکور سراسری این مباحث مورد بررسی قرار می‌گیرند.

در درس دوم این مجموعه الکتریسیته جاری مورد بحث قرار می‌گیرد و آموزش موضوعاتی نظیر جریان الکتریکی، قانون اهم، مقاومت الکتریکی، باتری و توان آن نیز پوشش داده می‌شوند. حل تست‌های کنکور سراسری مربوط به این مباحث پایان بخش این قسمت از آموزش‌ خواهد بود.

در ادامه و در درس سوم آموزش مطالب مربوط به مغناطیس ارائه شده است. این درس شامل بخش‌هایی نظیر مغناطیس و قطب‌های مغناطیسی، میدان مغناطیسی، میدان مغناطیسی زمین، میدان مغناطیسی یکنواخت، یکای میدان مغناطیسی و ویژگی‌های مواد مغناطیسی است. تست‌های سراسری مربوط به این مبحث نیز پایان بخش این فصل خواهد بود.

در درس چهارم و آخر این مجموعه آموزشی مطالبی در مورد القای الکترومغناطیس و جریان متناوب بیان شده است. لینک این آموزش نیز در ادامه آورده شده است.

این مجموعه آموزشی برای دانش‌آموزان پایه یازدهم و دانشجویان رشته‌های مهندسی و علوم پایه در درس فیزیک عمومی مفید خواهد بود.

• برای دیدن فیلم آموزش فیزیک یازدهم + اینجا کلیک کنید.

جمع‌بندی

در این مطلب در مورد نیروی الکتریکی و ویژگی‌های نیروی الکتریکی صحبت کردیم. همچنین مفهوم بار الکتریکی و مسائل مختلفی که با مفهوم نیروی الکتریکی و قانون کولن مورد بررسی قرار می‌گیرند را نیز مرور کردیم.