قانون آمپر — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در این مقاله قصد داریم تا با زبانی ساده به معرفی و بررسی قانون آمپر بپردازیم. با ما در ادامه همراه باشید. در مقاله «میدان الکتریکی (Electric Field) چیست؟ — از صفر تا صد» دیدیم که به منظور محاسبه میدان الکتریکی ناشی از یک توزیع بار می‌توانیم از رابطه $$dE = \int \frac{dq}{4 \pi \varepsilon_{0} r^{2}}$$ استفاده کنیم. به عبارت دیگر با تعیین میدان الکتریکی $$dE$$ ناشی از یک جزء بار $$dq$$ و سپس جمع‌زنی روی تمام میدان‌های الکتریکی ناشی از اجزای بار، می‌توانیم میدان الکتریکی کل را به‌دست آوریم. همچنین در مقاله «قانون گاوس (Gauss Law) و شار الکتریکی — یادگیری با مثال» با قانون گاوس آشنا شدیم و دیدیم که به منظور محاسبه میدان الکتریکی حاصل از یک توزیع یکنواخت بار که شکل و ساختار منظمی (متقارن) دارند (خط، استوانه‌ای، کروی و ...)، می‌توانیم از قانون گاوس به فرم $$\varepsilon_{0} \oint_{S} E.dS = q_{enc}$$ استفاده کنیم. استفاده از قانون گاوس، روند محاسبات را کاهش می‌دهد و روشی آسان‌تر (و البته محدود) جهت محاسبه میدان الکتریکی است. به عبارت دیگر استفاده از قانون گاوس بسته به شرایط مسئله می‌تواند بسیار ساده‌تر از حل معادله $$dE = \int \frac{dq}{4 \pi \varepsilon_{0} r^{2}}$$ باشد.

با مشابه حالت فوق، در مقوله مغناطیس نیز مواجه هستیم. در مقاله «میدان مغناطیسی جریان — از صفر تا صد» دیدیم که جهت محاسبه میدان مغناطیسی ناشی از جریان‌ الکتریکی (بار متحرک) در ساختاری همانند سیم، از قانون بیوساوار (Biot - Savart Law) به فرم $$d \overrightarrow{B} = \frac{\mu_{0}}{4 \pi} \frac{i d \overrightarrow{s} \times \hat{r}}{r^{2}}$$ استفاده می‌کنیم. به عبارت دیگر با استفاده از قانون بیوساوار می‌توانیم میدان مغناطیسی کل ناشی از هر توزیع جریان الکتریکی $$dI$$ را به دست آوریم.

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

حال اگر ساختار حامل جریان الکتریکی، شکلی منظم (متقارن) داشته باشد، جهت محاسبه میدان مغناطیسی می‌توان از معادله‌ای استفاده کرد که بسیار شبیه به معادله قانون گاوس است. این معادله به افتخار آندره مری آمپر (André-Marie Ampère) به قانون آمپر (Amperes law) موسوم است. به صورت کلی می‌توان قانون آمپر را نتیجه‌ای از قانون بیوساوار دانست. لازم به ذکر است که این قانون در واقع با کارهای جیمز کلرک ماکسول (James Clerk Maxwell) توسعه پیدا کرد.

قانون آمپر

قانون آمپر به فرم ساده زیر است:

$$\large \oint \overrightarrow{B} \cdot d \overrightarrow{l} = \mu_{0} i_{\mathrm{enc}}$$
(1)

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

در معادله فوق، $$\oint$$ به معنی انتگرال بسته است. به عبارت دیگر حاصل ضرب نقطه‌ای $$B.dl$$ باید به دور مسیری بسته (حلقه بسته) باشد. به زبان ساده $$\oint_{l}$$ به معنی محیط مسیر بسته است. این مسیر بسته به حلقه آمپر نیز معروف است. همانند قانون گاوس که در آن $$q_{\mathrm{enc}}$$ مقدار بار خالص درون سطح بسته گاوسی است، در اینجا نیز $$i_{\mathrm{enc}}$$ مقدار جریان خالص درون حلقه آمپر است. $$\mu_{0}$$ نیز نفوذپذیری (تراوایی) مغناطیسی با مقدار زیر است.

$$\large \mu_{0}=4 \pi \times 10^{-7} \mathrm{T} \cdot \mathrm{m} / \mathrm{A} \approx 1.26 \times 10^{-6} \mathrm{T} \cdot \mathrm{m} / \mathrm{A}$$
(2)

در ادامه به بررسی چند مثال کاربردی از قانون آمپر می‌پردازیم.

میدان مغناطیسی در اطراف سیم مستقیم بلند حامل جریان الکتریکی

مطابق با شکل زیر سیم بلندی را در نظر بگیرید که جریان الکتریکی $$i$$ از آن در جهت رو به بیرون صفحه (نمایش با علامت $$\circledcirc$$) می‌گذرد. در نظر داریم تا با استفاده از قانون آمپر (معادله 1) میدان مغناطیسی را در اطراف آن پیدا کنیم.

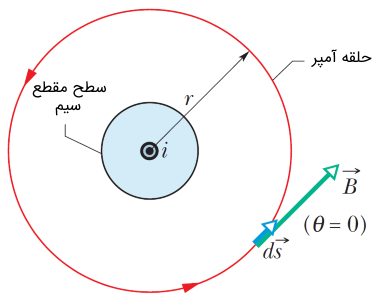
همان‌طور که از شکل فوق مشخص است، ساختار دارای تقارن بوده و میدان مغناطیسی در اطراف سیم حامل جریان برای هر جزء از سیم دارای تقارن است. بهترین شکلی که می‌توان به عنوان حلقه آمپر در نظر گرفت دایره‌ای به شعاع $$r$$ است. از آنجایی که جهت جریان الکتریکی رو به بالا است، مطابق با قانون دست راست، جهت میدان مغناطیسی در جهتی است که در شکل (۲) روی حلقه آمپر نشان داده شده است (فلش کوچک روی حلقه آمپر).

بنابراین مسیر انتگرال‌گیری پادساعتگرد بوده و در نتیجه جهت جز دیفرانسیلی $$dl$$ در جهت میدان مغناطیسی است (در شکل جزء دیفرانسیلی طول با $$ds$$ نمایش داده شده است؛ $$ds = dl$$). یعنی:

$$\large \begin{equation} \oint \overrightarrow{B} \cdot d \overrightarrow{l} = \oint B \cos \theta d l=B \oint d l = B(2 \pi r) \end{equation}$$
(3)

توجه داشته باشید که در اینجا مجموع تمامی جزهای دیفرانسیلی $$dl$$ روی حلقه آمپر که آن را به شکل دایره در نظر گرفتیم، برابر با محیط دایره $$2\pi r$$ می‌شود. از آنجایی که در حلقه آمپر تنها جریان $$i$$ قرار دارد، پس سمت راست قانون آمپر نیز برابر با $$\mu_{0}i$$ می‌شود. در نتیجه داریم:

$$\large \begin{equation}B=\frac{\mu_{0} i}{2 \pi r}\end{equation}$$
(4)

همان‌طور که مشاهده کردید، روند محاسبات میدان مغناطیسی با استفاده از قانون آمپر، بسیار ساده‌تر و سریع‌تر از قانون بیوساوار است.

میدان مغناطیسی درون سیم مستقیم بلند حامل جریان الکتریکی

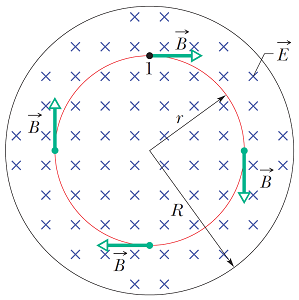
در قسمت قبل میدان مغناطیسی را در خارج (اطراف) از سیم مستقیم و بلند حامل جریان محاسبه کردیم. در اینجا در نظر داریم تا میدان مغناطیسی را درون سیم مذکور به دست آوریم. مطابق با شکل زیر، سیم مستقیم و بلند حامل جریان را با شعاع $$R$$ در نظر بگیرید.

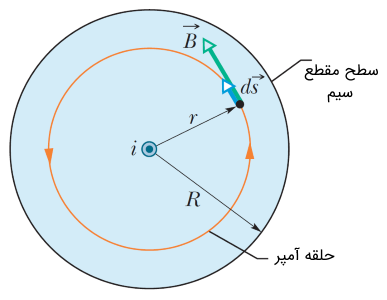
مطابق با قانون آمپر، متناسب با ساختار متقارن جسم مذکور، حلقه‌ آمپر را به شکل دایره‌ای با شعاع $$r$$ درون سیم در نظر می‌گیریم (حلقه نارنجی رنگ). در اینجا نیز جهت جریان الکتریکی به سمت خارج از صفحه و جهت میدان مغناطیسی و مسیر انتگرال‌گیری به صورت پادساعتگرد است. یعنی:

$$\large \begin{equation}\oint \overrightarrow{B} \cdot d \overrightarrow{l} = B \oint d l = B(2 \pi r)\end{equation}$$
(5)

گفتیم که سمت راست معادله قانون آمپر شامل جریان خالصی است که حلقه آمپر آن را در بر می‌گیرد. از آنجایی که ساختار شکل (3) متقارن است، توزیع جریان الکتریکی، در واقع چگالی جریان الکتریکی به صورت زیر است:

$$\large J=\frac{i}{A} \rightarrow J_{enc}=J_{T} \rightarrow \frac{i_{enc}}{\pi r^2}=\frac{i}{\pi R^2}$$
(6)

با توجه به این که چگالی جریان، جریان بر واحد سطح تعریف می‌شود، پس جریان محصور شده توسط حلقه آمپر به صورت زیر نتیجه می‌شود:

$$\large \begin{equation}i_{\mathrm{enc}}=i \frac{\pi r^{2}}{\pi R^{2}}\end{equation}$$
(7)

عبارت فوق با ضرب شدن در $$\mu_{0}$$ سمت راست معادله قانون آمپر را تشکیل می‌دهد. با توجه به مطالب فوق، میدان مغناطیسی درون سیم مستقیم و بلند حامل جریان به صورت زیر نتیجه می‌شود:

$$\large \begin{equation}B=\left(\frac{\mu_{0} i}{2 \pi R^{2}}\right) r\end{equation}$$
(8)

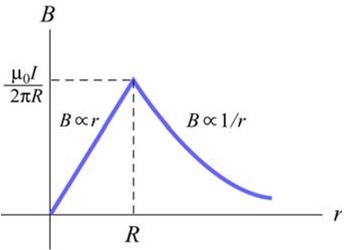
تعمیم قانون آمپر

قانون آمپر که در قسمت قبل مورد بررسی قرار گرفت، تنها برای جریان‌های الکتریکی ثابت مورد استفاده است. با در نظر گرفتن رابطه $$\mu_{0}$$ با چگالی شار میدان مغناطیسی ($$B = \mu_{0} H$$) داریم:

$$\large \oint_{c} H.dl = I$$
(9)

فیلم آموزش الکترومغناطیس مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

در مقاله «القای الکترومغناطیسی (Electromagnetic Induction) — از صفر تا صد» دیدیم که میدان‌های الکتریکی متغیر با زمان می‌توانند باعث ایجاد میدان مغناطیسی شوند. این امر به زبان ریاضی به صورت زیر وارد معادله قانون آمپر می‌شود:

$$\large \oint_{C} H.dl = \frac{\text{d}}{\text{d}t} \oint_{S} D.dS + I$$
(10)

رابطه فوق که به تعمیم قانون آمپر موسوم است، توسط ماکسول پیشنهاد شد. با وارد کردن جمله $$\frac{\text{d}}{\text{d}t} \oint_{S} D.dS$$ به قانون آمپر، ماکسول توانست اشکالات کلیه روابط الکترومغناطیسی را برطرف کند و مجموعه‌ای سازگار از نظریه الکترومغناطیسی را ارائه کند. چهار معادله زیر که به معادلات ماکسول معروف هستند، می‌توانند تمامی پدیده‌های الکترومغناطیسی را در حوزه فیزیک کلاسیک تشریح کنند. وارد کردن این معادلات به حوزه‌های نسبیتی و کوانتومی خود نیازمند تغییراتی است.

$$\large \begin{equation} \oint_{S} D \cdot d S = \int_{V} \rho d V \end{equation}$$
(11)

$$\large \begin{equation} \oint_{S} B \cdot d S = 0 \end{equation}$$
(12)

$$\large \begin{equation} \oint_{C} E \cdot d l = -\frac{d}{d t} \int_{S} B \cdot d S \end{equation}$$
(13)

$$\large \begin{equation} \oint_{C} H \cdot d l = \int_{S} J \cdot d S+\frac{d}{d t} \int_{S} D \cdot d S \end{equation}$$
(14)

پیشنهاد می‌کنیم تا نگاهی بر مقاله «فرم دیفرانسیلی معادلات ماکسول -- به زبان ساده» داشته باشید تا با نحوه به دست آوردن فرم دیفرانسیلی آن‌ها از فرم انتگرالی فوق، آشنا شوید. این معادلات به شکل زیر هستند:

$$\large \triangledown.D=\rho$$
(15)

$$\large \triangledown.B=0$$
(16)

$$\large \triangledown \times E=-\frac{\partial B}{\partial t}$$
(17)

$$\large \triangledown \times H=\frac{\partial D}{\partial t}+J$$
(18)

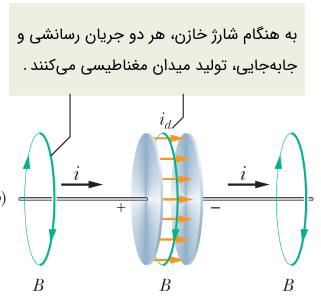
در صورتی که با جریان‌های ثابت سروکار داشته باشیم، واضح است که جمله $$\frac{\text{d}}{\text{d}t} \oint_{S} D.dS$$ در معادله (10) صفر شده و قانون آمپر به شکل ساده $$\large \oint_{c} H.dl = I$$ در می‌آید. این رابطه به قانون آمپر در مگنتواستاتیک نیز موسوم است. اغلب به جمله $$\frac{\text{d}}{\text{d}t} \oint_{S} D.dS$$ جریان جابه‌جایی گفته و آن را با نماد $$I_{D}$$ نشان می‌دهند. در نتیجه سمت راست قانون آمپر شامل دو نوع جریان است، یکی جریان رسانشی $$I$$ و دیگری جریان جابه‌جایی $$I_{D}$$. ماکسول جمع این دو جریان را، تنها جریان الکتریکی ($$i = I_{D} + I$$) نامید.

رابطه (10) را می‌توان به شکل زیر نیز نوشت. که در اغلب مراجع از آن به نام قانون آمپر - ماکسول (Ampere - Maxwell Law) یاد می‌کنند.

$$\large \begin{equation} \oint_{C} \overrightarrow{B} \cdot d \overrightarrow{l} = \mu_{0} \varepsilon_{0} \frac{d \Phi_{E}}{d t} + \mu_{0} i_{\mathrm{enc}} \end{equation}$$
(19)

عبارت $$\frac{d \Phi_{E}}{d t}$$، تغییرات شار الکتریکی با زمان است. همان‌طور که پیش‌تر بیان کردیم، در صورتی که در یک سیم جریان ثابتی برقرار باشد، تغییرات شار الکتریکی وجود نداشته و در نتیجه جریان جابه‌جایی صفر است. اما در صورتی که شار الکتریکی تغییر کند اما جریانی برقرار نباشد، مثلاً بین صفحات خازن، تنها جریان جابه‌جایی داریم.

اجازه دهید این مطلب را با همان مثال خازن ادامه دهیم. قبل از اضافه کردن جمله جریان جابه‌جایی $$I_{D}$$ توسط ماکسول به قانون آمپر، یکی از موارد پر ابهام، چگونگی عبور جریان در مداری شامل خازن بود. مداری را فرض کنید که تنها شامل یک خازن و منبع جریان باشد. در این حالت جریان الکتریکی وارد صفحه مثبت خازن شده و از صفحه منفی آن خارج می‌شود.

سوالی که در اینجا مطرح می‌شود، چگونگی پیوستگی جریان الکتریکی است. در واقع بین صفحات خازن که با یکدیگر فاصله دارند، جریان چگونه منتقل می‌شود؟ با توجه به شکل زیر اگر سطح بسته‌ای را طوری انتخاب کنیم که از میان صفحات خازن بگذرد، در این صورت جریان از یک سمت وارد و از سمت دیگر خارج نمی‌شود.

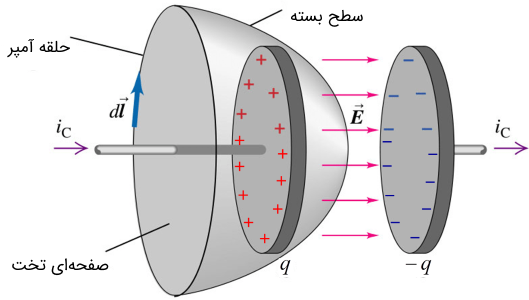
این ابهام با تعمیم قانون آمپر به راحتی حل‌ و فصل می‌شود. بر اساس نظر ماکسول، جریان الکتریکی تنها از نوع رسانشی نبوده و بلکه جریان الکتریکی کل، مجموع جریان رسانشی ($$I$$) و جریان جابه‌جایی ($$I_{D}$$) است. در مورد خازن، جریان الکتریکی از طریق جریان جابه‌جایی بین صفحات آن منتقل می‌شود. به عبارت دیگر در سیم‌های مدار، جریان الکتریکی کل (i) به دلیل صفر بودن جریان جابه‌جایی $$I_{D}$$، تنها برابر با $$I$$ یعنی جریان رسانشی است. بین صفحات خازن نیز جریان رسانشی صفر بوده و جریان کل تنها برابر با جریان جابه‌جایی $$i = I_{D}$$ است.

با توجه به مطالب فوق، مقدار جریان جابه‌جایی بین صفحات خازن باید با مقدار جریان رسانشی در سیم‌های مدار مساوی باشد. جهت بررسی این تساوی، فرض کنید که منبع تولید جریانی با اختلاف پتانسیل متغیر $$\frac{dV}{dt}$$ از طریق سیم‌هایی به یک خازن متصل است. جریان رسانشی (هدایتی) $$I$$ برابر است با:

$$\large I = \frac{dq}{dt} = C \frac{dV}{dt}$$
(20)

توجه داشته باشید که بار الکتریکی جمع شده در صفحات یک خازن به صورت $$q = CV$$ است. حال به محاسبه جریان جابه‌جایی می‌پردازیم. طبق رابطه (10) داریم:

$$\large I_{D} = \oint_{S} D.dS = \frac{\text{d}}{\text{d}t} (DS)$$
(21)

در رابطه فوق، $$S$$ مساحت صفحات خازن مذکور و $$D$$ مقدار جابه‌جایی الکتریکی است. در اینجا به دلیل یکنواخت بودن میدان الکتریکی بین صفحات خازن (البته متغیر به دلیل منبع ولتاژ متغیر با زمان) مقدار انتگرال فوق به راحتی برابر با $$DS$$ می‌شود. در مقاله «دی‌الکتریک -- به زبان ساده» دیدیم که جابه‌جایی الکتریکی $$D$$ با شدت میدان الکتریکی $$E$$ به صورت $$D = \varepsilon_{0}E$$ رابطه دارد. در نتیجه معادله (21) به شکل زیر در می‌آید:

$$\large I_{D} = \frac{\text{d}}{\text{d}t} (DS) = \varepsilon_{0} S \frac{\text{d}E}{\text{d}t}$$
(22)

می‌دانیم که میدان الکتریکی با ولتاژ به صورت $$V = Ed$$ ارتباط دارد. در نتیجه:

$$\large I_{D} = \frac{\text{d}}{\text{d}t} (DS) = \varepsilon_{0} S \frac{\text{d}}{\text{d}t}\frac{V}{d}$$

$$\large I_{D} = C \frac{\text{d}V}{\text{d}t}$$
(23)

در عبارت فوق، $$\varepsilon_{0}\frac{S}{d}$$ ظرفیت خازن بوده که در مقاله «ظرفیت خازن -- یادیگری با مثال» آن را محاسبه کردیم. همان‌طور که مشاهده می‌کنید، مقدار جریان جابه‌جایی بین صفحات خازن با مقدار جریان رسانشی که در سیم‌های مدار جریان دارد برابر است. اگر بین صفحات خازن، ماده‌ دی‌الکتریک با رسانایی ویژه σ قرار داشته باشد، در این صورت مقداری از جریان رسانشی که در سیم‌های مدار جریان دارد از خازن نیز عبور کرده که در این صورت قسمتی از جریان داخل خازن نیز رسانشی می‌شود. در اینجا نیز دقت داشته باشید که مقدار جریان داخل خازن پر شده با دی‌الکتریک ($$k$$) با جریان رسانشی که از سیم‌ها عبور می‌کند، باید برابر باشد.

میدان مغناطیسی حاصل از جریان جابه‌جایی بین صفحات خازن

خازنی تخت با صفحات دایروی که بین آن‌ها از هوا پر شده است را در نظر بگیرید. فاصله بین صفحات دایروی $$d$$ است (شکل ۸). خازن مذکور به یک منبع ولتاژ متصل بوده که ولتاژ دوسر آن به صورت $$\frac{dV}{dt}$$ تغییر می‌کند. در اینجا قصد داریم تا به محاسبه میدان مغناطیسی بین صفحات خازن بپردازیم.

در اینجا از معادله (19) استفاده می‌کنیم. شار الکتریکی بین صفحات خازن (از قانون گاوس) به صورت زیر محاسبه می‌شود:

$$\large \Phi_{E} = \int D.dS = \varepsilon_{0} \pi r^{2} E$$
(24)

$$\large \Phi_{E} = \varepsilon_{0} \pi r^{2} (\frac{V}{d})$$
(25)

در رابطه فوق از رابطه میدان الکتریکی با ولتاژ به صورت $$V = Ed$$ استفاده کردیم. با گرفتن مشتق زمانی از رابطه فوق، جریان جابه‌جایی $$I_{D}$$ نتیجه می‌شود.

$$\large I_{D} = \frac{\text{d}}{\text{d}t} \int D.dS = \frac{\text{d}}{\text{d}t} (\varepsilon_{0} \pi r^{2} \frac{V}{d}) = \frac{\varepsilon_{0} \pi r^{2}}{d} \frac{\text{d}V}{\text{d}t}$$
(26)

از آنجایی که جریان رسانشی بین صفحات خازن پر شده با هوا صفر است، جریان داخل خازن تنها برابر با جریان جابه‌جایی $$I_{D}$$ است. در نتیجه بر اساس قانون آمپر داریم:

$$\large \oint_{c} H.dl = I_{D}$$
(27)

به دلیل تقارن ساختار، پارامتر $$H$$ (شدت میدان مغناطیسی) به راحتی از انتگرال بیرون آمده و حاصل $$\oint_{C} dl$$ برابر با محیط صفحات دایروی خازن است. در نتیجه:

$$\large H 2 \pi r = \frac{\varepsilon_{0} \pi r^{2}}{d} \frac{\text{d}V}{\text{d}t}$$

$$\large \Rightarrow H = \frac{\varepsilon_{0} r}{2d} \frac{\text{d}V}{\text{d}t}$$
(28)

عبارت فوق بر حسب چگالی شار مغناطیسی به صورت زیر است:

$$\large \Rightarrow B = \mu_{0} H = \frac{\mu_{0} \varepsilon_{0} r}{2d} \frac{\text{d}V}{\text{d}t}$$
(29)

در عبارت فوق حاصل $$\mu_{0} \varepsilon_{0}$$ به صورت $$\mu_{0} \varepsilon_{0} = \frac{1}{c^{2}}$$ است که در آن $$c$$ سرعت نور است. مقدار $$B$$ بسیار اندک بوده و به همین علت در عمل از مقدار آن بین صفحات خازن صرف نظر می‌کنند.

اگر مطالب ارائه شده در این مقاله برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آنتن و فرستنده -- به زبان ساده
• امواج رادیویی -- به زبان ساده
• طیف مرئی -- به زبان ساده

^^