تحلیل ابعادی (Dimensional Analysis) در مکانیک سیالات – به زبان ساده

مفهوم تحلیل ابعادی کاربرد بسیار زیادی در علم مکانیک دارد. در این علم، برای استفاده از نتایج آزمایشگاهی در کاربردهای صنعتی باید اندازه‌ها و نتایج را مقیاس کنیم. مقیاس کردن در مسائل مختلف مکانیک سیالات به کمک اعداد بی‌بعد انجام می‌شود. برای مثال، زمانی نتایج یک تست آزمایشگاهی روی ماکت کوچک بال هواپیما می‌تواند برای طراحی بال واقعی هواپیما مورد استفاده قرار بگیرد که اعداد بی‌بعد مانند رینولدز در ماکت و بال واقعی هواپیما یکسان باشند.

محاسبه این اعداد بی‌بعد در هر مسئله خاص با استفاده از روشی به نام تحلیل ابعادی انجام می‌شود. در این مطلب ابتدا تئوری پی باکینگهام مورد بررسی قرار می‌گیرد و در ادامه روش تحلیل ابعادی به صورت گام به گام آموزش داده می‌شود و در انتها با استفاده از یک مثال، کاربرد روش معرفی شده در این مطلب برای تحلیل ابعادی مسائل مکانیک سیالات مورد بررسی قرار می‌گیرد.

تئوری پی باکینگهام

نکته اساسی در تحلیل ابعادی یک سیستم، تعیین تعداد پارامترهای بی‌بعدی است که می‌توان آن‌ها را جایگزین متغیرهای اصلی کرد. تئوری پی باکینگهام به بررسی این موضوع می‌پردازد. این تئوری به شکل زیر بیان می‌شود:

«اگر یک معادله که از نظر ابعادی همگن و شامل k متغیر است را در نظر بگیریم. این معادله را می‌توان با استفاده از رابطه بین k-r متغیر بدون بعد مستقل نیز بیان کرد. در اینجا r کمترین تعداد بعدهای مرجع مورد نیاز برای تعریف متغیرها را نشان می‌دهد.»

اعداد بی‌بعد نهایی را «ترم‌های پی» (Pi terms) و عبارت فوق را «تئوری پی باکینگهام» (Buckingham pi theorem) می‌نامند. ادگار باکینگهام از علامت $$\pi$$ برای نمایش متغیرهای بی‌بعد استفاده کرد. این نماد به صورت رایج در سایر مسائل مکانیک سیالات نیز مورد استفاده قرار می‌گیرد. توجه کنید که اگرچه تئوری پی باکینگهام ساده به نظر می‌رسد ولی اثبات آن به این سادگی نیست و در این مطلب آورده نشده است.

همانطور که در متن تئوری پی باکینگهام اشاره شد، این تئوری برای معادله‌ای صادق است که از نظر ابعادی همگن باشد. برای توضیح این موضوع، معادله‌ای شامل‌ k متغیر به شکل زیر را در نظر بگیرید.

برای اینکه معادله فوق از نظر ابعادی همگن باشد، باید «دیمانسیون» (Dimensions) متغیر سمت چپ معادله با دیمانسیون کلی تمام ترم‌های سمت راست معادله برابر باشد. تابع بالا با استفاده از ترم‌های $$\pi$$ (متغیرهای بی‌بعد)، به شکل زیر بیان می‌شود:

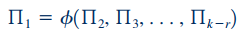
تعداد ترم‌های $$\pi$$ در این رابطه (k-r) نسبت به تعداد متغیرهای رابطه اصلی به میزان r عدد کمتر است. r برابر با کمترین تعداد «بعد‌های مرجع» (Reference Dimensions) مورد نیاز برای تعریف متغیرهای رابطه اصلی است.

معمولا بعدهای مرجع که برای توصیف متغیرها مورد استفاده قرار می‌گیرند، همان «بعدهای پایه» (Basic Dimensions) مانند M ،L و T یا F ،L و T هستند. البته ممکن است در برخی حالات فقط دو متغیر مانند L و T و یا تنها یک متغیر مانند L کافی باشد. حالات بسیار کم‌یابی نیز هستند که در آن‌ها متغیرها براساس ترکیبی از این بعد‌های پایه توصیف می‌شوند. مانند $$M/T^{2}$$ و L. در این مثال، r در تئوری پی باکینگهام باید برابر با 2 در نظر گرفته شود. در ادامه به بررسی روند استفاده از تئوری پی باکینگهام برای تعریف متغیرهای بی‌بعد پرداخته می‌شود.

مشخص کردن ترم‌های $$\pi$$ در تئوری پی باکینگهام برای تحلیل ابعادی

روش‌های متعددی برای تحلیل ابعادی موجود هستند که این روش‌ها در نهایت منجر به تولید اعداد بی‌بعد و ترم‌های $$\pi$$ در معادله پی باکینگهام می‌شوند. در ادامه و به طور دقیق روشی مورد بررسی قرار خواهد گرفت که متغیرهای ‌بی‌بعد را به صورت گام به گام و مستقل از هم تولید کند. این روش موسوم به «روش تکرار متغیرها» (Method of Repeating Variables) است.

گام اول: مشخص کردن تمام متغیرهای موجود در مسئله

این مرحله سخت‌ترین و البته مهم‌ترین گام در تحلیل ابعادی به کمک روش ارائه شده در این مطلب است. در این مرحله تمامی متغیرهای موجود در مسئله (بی‌بعد و بابعد) باید به درستی مشخص بشوند، در غیر این صورت تحلیل ابعادی به درستی صورت نخواهد گرفت.

این متغیرها با استفاده از قوانین فیزیکی حاکم بر پدیده مورد بررسی و دانش آزمایشگاهی برای انجام آزمایشات مربوط به آن، تعیین می‌شوند. برای مثال این مجموعه حتما باید شامل متغیرهایی باشد که توانایی توصیف هندسه سیستم را داشته باشند. همچنین این متغیرها باید به گونه‌ای تعیین شوند که بتوانند توصیف خوبی از خواص سیال مانند ویسکوزیته و عوامل خارجی وارد بر سیستم مانند افت فشار را ارائه دهند.

نکته‌ای که باید به آن توجه کرد این است که در مسائل مختلف، احتمالاً متغیرهایی موجود هستند که در تقسیم‌بندی بالا حضور ندارند. بنابراین باید متغیرهای تاثیرگذار در هر مسئله به صورت دقیق مورد ارزیابی قرار بگیرند.

در اعلام لیست متغیرها باید توجه داشت که هدف ما یافتن کمترین تعداد متغیری است که به کمک آن‌ها، خواص سیستم به صورت کامل توصیف شود. بنابراین تنها متغیرهایی را در نظر می‌گیریم که مستقل از یکدیگر هستند. برای مثال در صورتی که مساحت مقطع یک لوله و قطر آن پارامتر‌های مهمی برای توصیف ویژگی‌های سیستم باشند، تنها یکی از این دو متغیر را در لیست متغیرهای موجود در این مسئله اعلام می‌کنیم.

گام دوم: بیان متغیرهای مسئله برحسب ابعاد پایه

ابعاد پایه‌ در مسائل مکانیک سیالات عموماً M ،L و T یا F ،L و T هستند و در یک مسئله تحلیل ابعادی باید تنها از یکی از این گروه‌های نام‌گذاری استفاده کرد. این دو گروه از متغیرها با استفاده از قانون دوم نیوتن و به شکل زیر به یکدیگر مرتبط می‌شوند.

برای مثال چگالی را می‌توان به کمک این گروه به شکل زیر نمایش داد.

گام سوم: تعیین تعداد ترم‌های $$\pi$$ مورد نیاز

در این قسمت از تئوری پی باکینگهام استفاده می‌شود. این تئوری بیان می‌کند که تعداد ترم‌های $$\pi$$ برابر با k-r است. در این رابطه k تعداد متغیرهای مسئله است که در گام اول محاسبه شد و r برابر با تعداد ابعاد مرجع مورد نیاز برای تعریف متغیرهای مسئله در نظر گرفته می‌شود. در اکثر حالات تعداد ابعاد مرجع و تعداد ابعاد پایه برای تعریف متغیرهای مسئله یکسان هستند ولی در برخی از مسائل برای تعریف متغیرهای مسئله در گام دوم نیاز به ترکیبی از ابعاد پایه داریم که در این حالت تعداد ابعاد مرجع کمتر از تعداد ابعاد پایه خواهند بود.

گام چهارم: تعیین تعداد متغیرهای تکرار شونده

متغیرهای تکرار شونده آن دسته از متغیرهایی هستند که در تمام ترم‌های $$\pi$$ مورد استفاده قرار می‌گیرند. تعداد این متغیرهای تکرار شونده در گام چهارم برابر با تعداد ابعاد مرجع در نظر گرفته می‌شوند و در اکثر مسائل برابر با تعداد ابعاد پایه نیز هستند.

برای تعیین متغیرهای تکرار شونده، از لیست متغیرهایی که در گام اول مشخص شدند، آن‌هایی را انتخاب می‌کنیم که می‌توانند با یکدیگر ترکیب شوند و یک ترم $$\pi$$ را تولید کنند. توجه شود که هرکدام از این متغیرهای تکرار شونده باید از نظر ابعادی مستقل از یکدیگر باشند به طوری که نتوان یک متغیر تکرار شونده را با استفاده از ترکیبی از سایر متغیرهای تکرار شونده تولید کرد.

گام پنجم: محاسبه اولین پارامتر بی‌بعد $$\pi$$

در این قسمت پارامتر بی‌بعد اول محاسبه می‌شود. برای این منظور، ترم بی‌بعد $$\pi$$ را به صورت حاصل ضرب متغیرهای تکرار شونده در یکی از متغیرهای باقی‌مانده مانند رابطه زیر می‌‌نویسیم.

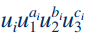
در این رابطه u₂ ،u₁ و u₃ متغیرهای تکرار شونده هستند و $$u_{i}$$ یکی از متغیرهای باقی‌مانده است. b_{i ،}a_i و c_i نیز برای این استفاده شده‌اند که عبارت رابطه فوق بی‌بعد باشد. در این رابطه b_{i ،}a_i و c_i مجهول هستند و با نوشتن یک دستگاه معادلات چند مجهولی می‌توان مقدار آن‌ها را محاسبه کرد.

گام ششم: تکرار گام پنجم برای سایر متغیرهای باقی‌مانده

در این مرحله، همان فرآیندی که در مرحله پنجم انجام دادیم را برای تمام متغیرهای باقی‌مانده تکرار می‌کنیم. نکته مهم این است که در نهایت تعداد ترم‌های $$\pi$$ باید برابر با همان عددی باشد که در مرحله سوم محاسبه شد. در غیر این صورت حتما اشتباهی رخ داده است و باید مراحل قبلی مورد ارزیابی قرار بگیرند.

گام هفتم: بررسی بی‌بعد بودن تمام ترم‌های $$\pi$$ محاسبه شده در گام پنجم و ششم

در این قسمت ابعاد متغیرها را در تمام ترم‌های $$\pi$$ قرار می‌دهیم و بُعد هرکدام از این ترم‌ها را محاسبه می‌کنیم و از بی‌بعد بودن آن‌ها مطمئن می‌شویم. این مرحله را می‌توان به کمک هر دو گروه متغیرهای پایه MLT و FLT انجام داد.

گام هشتم : نوشتن رابطه تابع نهایی

در این قسمت شکل نهایی تابع بر حسب پارامتر‌های بی‌بعد محاسبه شده، به شکل زیر در می‌آید:

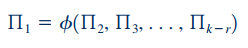
نکته مهم در اینجا این است که ترم $$\pi_{1}$$ شامل متغیر وابسته است. متغیر وابسته همان متغیری است که در گام اول، تمام متغیرهای موثر در تعیین آن را مشخص کردیم.

در ادامه با استفاده از یک مثال کاربرد گام‌های مختلف بالا در مسائل تحلیل ابعادی مکانیک سیالات نشان داده می‌شود.

مثال

جریان پایا، نیوتنی و غیرقابل تراکم سیال را در نظر بگیرید که مطابق شکل در یک لوله طویل، دایروی، افقی و با سطوح صاف جریان دارد. هدف مسئله، محاسبه افت فشار در طول لوله است که رابطه آن به شکل زیر نمایش داده می‌شود.

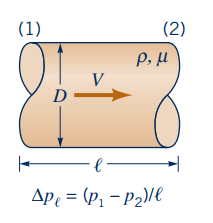
گام اول در تحلیل ابعادی، مشخص کردن تمام متغیرهای موجود در مسئله است. در اینجا بر اساس اطلاعات تجربی متغیرهای موثر در افت فشار لوله به شکل زیر نمایش داده می‌شوند.

در  تابع بالا، D قطر لوله، $$\rho$$ چگالی سیال، $$\mu$$ ویسکوزیته سیال و V سرعت میانگین سیال در لوله را نشان می‌دهند.

در گام دوم تحلیل ابعادی، متغیرهای مسئله باید برحسب ابعاد پایه‌ بیان شوند. برای این منظور، F ،L و T به عنوان ابعاد پایه‌ در نظر گرفته می‌شوند. بنابراین داریم:

در صورتی که ابعاد پایه را در مرحله قبل برابر با M ،L و T در نظر می‌گرفتیم نیز، نتیجه نهایی یکسان می‌شد ولی باید توجه کرد که نمی‌توان هر دو گروه ابعاد پایه (M ،L و T یا F ،L و T) را با یکدیگر ترکیب کرد و در هر مسئله، تنها یکی از گرو‌ه‌های ابعاد پایه رایج باید مورد استفاده قرار بگیرد.

گام سوم تحلیل ابعادی، به کار بستن تئوری پی باکینگهام برای تعیین تعداد ترم‌های $$\pi$$ در این مسئله است. در این مثال k (متغیرهایی که در گام دوم بر حسب ابعاد پایه بیان شدند) برابر با 5 و r (تعداد ابعاد مرجع F ،L و T) برابر با ۳ است. بنابراین با توجه به تئوری پی باکینگهام، دو (3-5) ترم‌ پی برای توصیف این سیستم با استفاده از اعداد بی‌بعد مورد نیاز است.

در گام چهارم تحلیل ابعادی، باید متغیرهای تکرار شونده برای تعیین ترم‌های پی، مشخص شوند. در این مثال، متغیرهای تکرار شونده باید از بین D، $$\rho$$، $$\mu$$ و V انتخاب گردند. نکته مهم این است که متغیر وابسته یعنی افت فشار به عنوان متغیر تکرار شونده در نظر گرفته نمی‌شود.

در این مسئله تعداد ابعاد مرجع مورد نیاز برابر با ۳ است؛ بنابراین باید سه متغیر تکرار شونده نیز انتخاب شود. در این گام برای ساده‌سازی مسئله متغیرهایی را به عنوان متغیر تکرار شونده در نظر می‌گیریم که از نظر ابعادی ساده و مستقل از یکدیگر باشند. برای مثال در این مسئله $$\rho$$، D و V به عنوان متغیرهای تکرار شونده در نظر گرفته می‌شوند. مستقل بودن این سه متغیر نسبت به یکدیگر، نشان می‌دهد که نمی‌توان با استفاده از آن‌ها، یک عبارت بی‌بعد را تولید کرد.

در گام پنجم تحلیل ابعادی، باید یکی از ترم‌های $$\pi$$ محاسبه شود. در گام سوم مشخص شد که تنها دو ترم $$\pi$$ برای این مسئله مورد نیاز است. بنابراین ترم اول $$\pi$$ به صورت حاصل ضرب متغیر وابسته (تغییر فشار) در سه متغیر تکرار شونده به فرم زیر نوشته می‌شود.

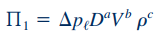
فرم نهایی رابطه بالا باید به صورت بی‌بعد باشد. برای بررسی بی‌بعد بودن این رابطه، ابتدا باید آن را برحسب متغیرهای پایه به صورت زیر بازنویسی کرد.

در رابطه بالا باید توان‌ نهایی هرکدام از ابعاد پایه F ،L و T برابر با صفر باشد. بنابراین سه معادله و سه مجهول به شکل زیر داریم:

با حل دستگاه معادلات فوق، نتایج نهایی به صورت b=-2 ،a=1 و c=-1 محاسبه می‌شوند و در نهایت رابطه زیر را برای ترم بی‌بعد $$\pi$$ داریم:

در گام ششم تحلیل ابعادی، ترم بی‌بعد ‌$$\pi$$ را با ترکیب سه متغیر تکرار شونده و متغیر باقی‌مانده یعنی $$\mu$$ به شکل زیر می‌نویسیم.

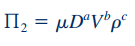
رابطه بالا را می‌توان بر حسب متغیرهای پایه به شکل زیر نمایش داد:

در ادامه با صفر قرار دادن توان هرکدام از ابعاد پایه به سه معادله و سه مجهول زیر می‌رسیم.

در نهایت نیاز به حل دستگاه معادلات فوق داریم و با حل این معادلات، نتایج نهایی به صورت b=-1 ،a=-1 و c=-1 محاسبه می‌شوند و رابطه زیر برای ترم بی‌بعد $$\pi$$ به‌ دست می‌آید:

در گام هفتم تحلیل ابعادی، باید با استفاده از هر دو گروه ابعاد پایه MLT و FLT، بی‌بعد بودن ترم‌های $$\pi$$ چک شوند. بنابراین داریم:

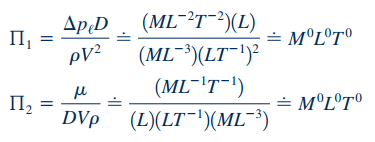
در نهایت و در گام هشتم، نتیجه نهایی تحلیل ابعادی به شکل زیر بیان می‌شود.

عبارت فوق نشان می‌دهد که این مسئله را می‌توان با استفاده از دو ترم $$\pi$$ معرفی شده به جای ۵ متغیر اولیه، مورد مطالعه قرار داد.

هشت گام مناسب برای تحلیل ‌ابعادی به صورت خلاصه در شکل زیر نشان داده شده‌اند.

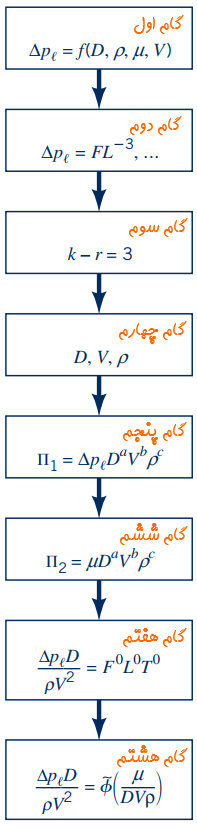
در این مطلب، تئوری پی باکینگهام و تحلیل ابعادی به صورت دقیق و کامل مطالعه شدند و در انتها نیز به کمک یک مثال، کاربرد روش معرفی شده برای تحلیل ابعادی مسائل مکانیک سیالات مورد بررسی قرار گرفت.

در صورتی که قصد یادگیری بیشتر در زمینه‌ مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• مجموعه آموزش‌های دروس مهندسی شیمی
• عدد رینولدز (Reynolds number) چیست؟ — از صفر تا صد
• پیوستگی و بقای جرم در سیالات — از صفر تا صد
• مومنتوم زاویه‌ای (Moment of Momentum) در سیالات — آموزش سریع و ساده
• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد

^^