تمرکز تنش در بارگذاری خمشی – به همراه مثال

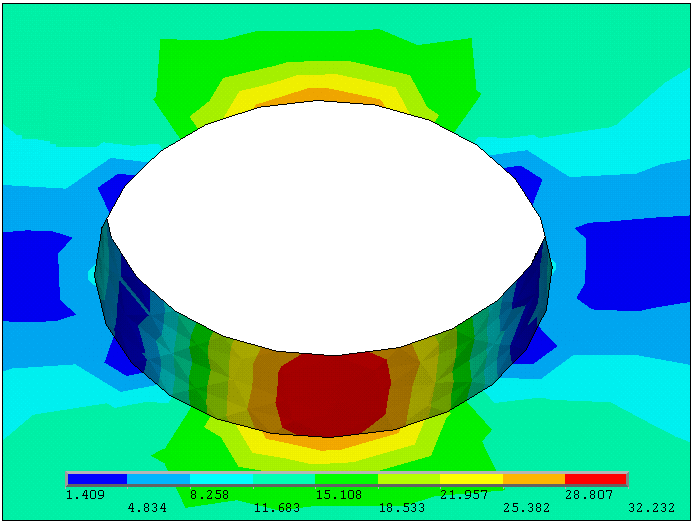
در مباحث «تنش‌های نرمال موجود در تیرها» و «تحلیل تنش‌های برشی در تیرهای مستطیلی» به معرفی رابطه خمش و رابطه پیچش برای تیرهای بدون حفره و شکاف پرداختیم. وجود حفره، شکاف و تغییرات ناگهانی ابعاد در تیرهای تحت بارگذاری باعث ایجاد تنش‌های زیاد در اطراف نواحی ناپیوستگی می‌شود. به تجمع تنش‌ها در کنار ناپیوستگی‌ها، «تمرکز تنش» (Stress Concentration) می‌گویند. در تحلیل مواد شکننده و حالت بارگذاری دینامیک، این پدیده اهمیت بسیار بالایی پیدا می‌کند. در این مقاله، به معرفی ساز و کار پدیده تمرکز تنش در بارگذاری خمشی خواهیم پرداخت. در انتها نیز، به منظور آشنایی بهتر با مفاهیم و روابط ارائه شده، یک مثال کاربردی را تشریح خواهیم کرد.

تمرکز تنش

در این بخش، برای ترسیم مفهوم بصری تمرکز تنش در بارگذاری خمشی، دو حالت از تمرکز تنش موجود در تیرها را توصیف می‌کنیم.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

حالت اول

در حالت اول، یک تیر مستطیلی به همراه یک حفره بر روی محور خنثی آن (شکل زیر) را مورد بررسی قرار می‌دهیم. ارتفاع این تیر برابر با h و ضخامت آن در راستای عمود بر صفحه برابر با b است. به علاوه، این تیر تحت خمش خالص ناشی از اعمال گشتاور خمشی M قرار دارد.

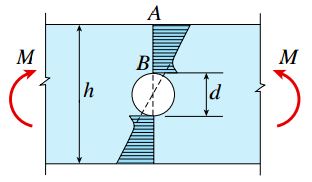
هنگامی که قطر حفره نسبت به ارتفاع تیر کوچک باشد، توزیع تنش بر روی مقطع عرضی گذرنده از حفره تقریباً مانند شکل بالا خواهد بود. در این حالت، تنش موجود بر روی نقطه B در لبه حفره بسیار بزرگ‌تر از تنش موجود بر روی همان نقطه در یک سطح مقطع بدون حفره است (خط چین‌های شکل بالا، توزیع تنش در سطح مقطع بدون حفره را نمایش می‌دهند). با دور شدن از حفره و نزدیک‌تر شدن به لبه تیر (نقطه A)، نمودار توزیع تنش نسبت به فاصله نقطه مورد بررسی تا محور خنثی به صورت خطی تغییر می‌کند. در این نواحی، تأثیر حضور حفره بر روی توزیع تنش بسیار کاهش می‌یابد.

در صورتی که ابعاد حفره نسبتاً بزرگ باشد، الگوی تنش تقریباً مشابه شکل زیر خواهد بود. با مقایسه این توزیع با توزیع تنش در تیر بدون حفره می‌توان مشاهده کرد که میزان تنش در نقطه B با یک افزایش بزرگ همراه بوده و تنش موجود در نقطه A با خط چین فاصله خیلی کمی دارد. تنش موجود در نقطه C نسبت به تنش نقطه A بیشتر اما نسبت به نقطه B کمتر است.

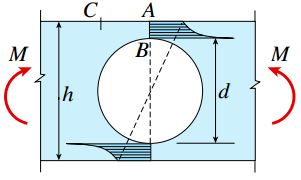
بررسی‌های گسترده نشان داده‌اند که تنش موجود در لبه حفره (نقطه B) تقریباً با «تنش اسمی» (Nominal Stress) همان نقطه برابر است. تنش اسمی معمولاً با استفاده از رابطه استاندارد خمش (σ=My/I) تعیین می‌شود. از این‌رو می‌توان از رابطه تقریبی زیر به منظور محاسبه تنش موجود در نقطه B استفاده کرد:

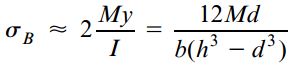
y: فاصله محور خنثی تا نقطه B (طول d/2 در شکل‌های بالا)؛ I: ممان اینرسی سطح مقطع خالص در محل وجود حفره

در لبه بیرونی تیر (نقطه C)، مقدار تنش تقریباً با تنش اسمی در نقطه A (مختصات y=h/2) برابر است:

با توجه به دو رابطه بالا، نسبت σ_B/σ_C تقریباً برابر با 2d/h خواهد بود. از این‌رو، زمانی که نسبت قطر حفره به ارتفاع تیر از ½ عبور کند، بیشترین تنش در نقطه B رخ می‌دهد. به این ترتیب اگر این نسبت از ½ کمتر باشد، بیشترین تنش به نقطه C اعمال خواهد شد.

حالت دوم

در حالت دوم، نحوه تمرکز تنش در یک تیر مستطیلی دارای شکاف را مورد بررسی قرار می‌دهیم. شکل زیر، یک نمونه از تیر مذکور با ارتفاع h و ضخامت b (در راستای عمود بر صفحه) را نمایش می‌دهد که در معرض خمش خالص قرار دارد. ارتفاع خالص تیر در محل شکاف (فاصله ابتدای هر شکاف) برابر با h₁ و شعاع آن در ابتدای هر شکاف برابر با R است.

حداکثر تنش اعمال شده بر این تیر در ابتدای هر شکاف رخ می‌دهد. مقدار تنش در این نقطه می‌تواند بسیار بیشتر از تنش اسمی محاسبه شده از رابطه خمش در همان نقطه باشد (y=h₁/2 و I=bh³/12):

تنش ماکسیمم با حاصل‌ضرب ضریب تمرکز تنش K در تنش اسمی برابر است:

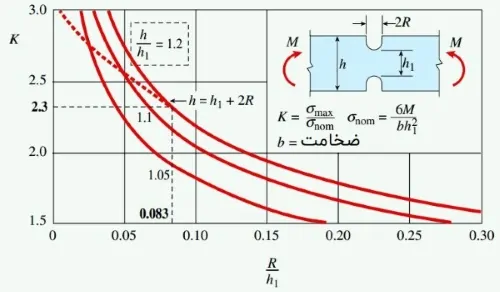
ضریب تمرکز تنش در شکل بالا برای برخی از مقادیر h/h₁ رسم شده است. توجه داشته باشید که با تیزتر شدن لبه‌های شکاف (کوچک‌تر شدن نسبت R/h₁)، ضریب تمرکز تنش افزایش می‌یابد. اثرات تمرکز تنش به نواحی کوچک در اطراف حفره‌ها و شکاف s محدود می‌شود.

بر اساس اصل سنت-ونانت، اگر فاصله نقطه مورد بررسی تا حفره درون تیر برابر یا بزرگ‌تر از h (ارتفاع مقطع) باشد، تأثیر تمرکز قابل چشم‌پوشی خواهد بود. در این حالت می‌توان از روابط کلی برای تحلیل تنش در آن نقطه استفاده کرد. در ادامه، به منظور آشنایی بهتر با نحوه تحلیل تمرکز تنش در تیرهای تحت پیچش، به تشریح کامل یک مثال می‌پردازیم.

مثال

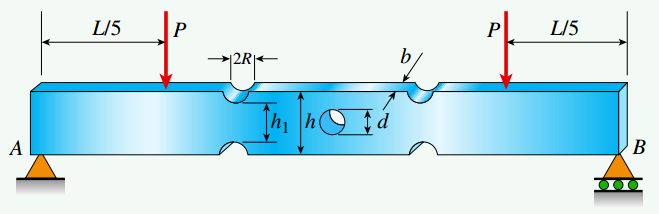
شکل زیر، یک تیر ساده با سطح مقطع مستطیلی (ابعاد b در h) نمایش می‌دهد که یک حفره با قطر d در مرکز طولی آن به همراه دو شکاف با فاصله‌ای برابر در دو طرف حفره وجود دارد. بارهای P در فاصله L/5 از دو انتهای تیر AB اعمال می‌شوند.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

با فرض فاصله L=4.5m، ضخامت تیر b=50mm، ارتفاع تیر h=144mm، فاصله بین شکاف‌ها h₁=120mm، قطر حفره d=85mm، شعاع شکاف‌ها R=10mm و تنش خمشی مجاز σ_a=150MPa، موارد زیر را تعیین کنید:

• الف) حداکثر مقدار مجاز برای بار P
• ب) کوچک‌ترین شعاع قابل قبول برای شکاف‌ها (R_min) با فرض P=11kN
• ج) حداکثر قطر قابل قبول برای حفره مرکزی تیر با فرض P=11kN

الف) حداکثر مقدار مجاز P

بخش مرکزی تیر در محدوده بین بارهای P (از x=L/5 تا x=4L/5)تحت خمش خالص قرار دارد و گشتاور ماکسیمم در این ناحیه برابر M=PL/5 است. برای تعیین P_max، باید تنش خمشی ماکسیمم (در بخش میانی اطراف حفره و در محل قرارگیری شکافs) را با تنش مجاز σ_a=150MPa مقایسه کنیم.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

به این منظور، ابتدا به بررسی تنش‌های ماکسیمم موجود در اطراف حفره می‌پردازیم. نسبت قطر حفره به ارتفاع تیر d/h=88/144=0.59 است. به دلیل عبور این نسبت از مقدار ½، تنش موجود در نقطه B در مقایسه با تنش موجود در نقطه C بیشتر خواهد بود. با جایگذاری σ_a به جای σ_B و PL/5 به جای M، رابطه مورد نیاز برای محاسبه P_max به دست می‌آید:

به این ترتیب، با استفاده از مقادیر عددی خواهیم داشت:

در مرحله بعد به منظور تعیین مقدار دوم P_max، تنش‌های حداکثری موجود در ابتدای هر دو شکاف را مورد بررسی قرار می‌دهیم. نسبت شعاع شکاف‌ها به فاصله آن‌ها (R/h₁) برابر با 0.083، نسبت ارتفاع تیر به ارتفاع شکاف‌ها (h/h₁) برابر با 1.2 و ضریب تمرکز تنش K تقریباً برابر با 2.3 است.

با توجه به روابط ارائه شده برای ضریب تمرکز تنش داریم:

به این ترتیب:

با مقایسه P_max1 و P_max2 می‌توان مشاهده کرد که تنش حداکثری موجود در ابتدای شکاف‌ها، عامل کنترل کننده حداکثر مقدار مجاز برای اعمال بار اعمال شده است:

ب) کوچک‌ترین شعاع قابل قبول برای شکاف‌ها

توجه داشته باشید در نمودار بالا، ضریب تمرکز تنش با کاهش نسبت R به h₁ افزایش می‌یابد. با استفاده از رابطه تنش اسمی داریم:

به منظور تعیین ضریب تمرکز تنش، تنش خمشی ماکسیمم σ_max را برابر تنش مجاز σ_a قرار می‌دهیم:

در نمودار زیر، با در نظر داشتن h/h₁=1.2 و K=1.82 داریم:

ج) حداکثر قطر قابل قبول برای حفره

برای حل این بخش از مثال، ابتدا فرض می‌کنیم که d/h>1/2 بوده و تنش خمشی ماکسیمم در نقطه B رخ می‌دهد. به این ترتیب می‌توانیم از رابطه σ_B برای تعیین d_max کنیم. اگر d/h کوچک‌تر از ½ باشد، تنش خمشی ماکسیمم در نقطه C رخ خواهد داد. در این صورت، از رابطه σ_C برای تعیین این تنش کمک می‌گیریم. در صورت اعمال تنش حداکثری در نقطه B خواهیم داشت:

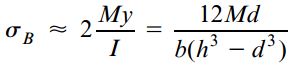
با قرار دادن مقادیر عددی در رابطه بالا، حداکثر قطر قابل قبول حفره برابر خواهد بود با:

از آنجایی که d_max/h=0.752، فرض اولیه ما مبنی بر رخ دادن تنش حداکثری در نقطه B تأیید می‌شود. در صورت عدم تأیید این فرض باید محاسبات بالا را بر حسب رابطه σ_C تکرار می‌کردیم.

^^