تنش های نرمال موجود در تیرها – با مثال های کاربردی
در مبحث «تعیین کرنش درون تیرها»، به ارزیابی کرنشهای طولی εx در هنگام اعمال خمش خالص بر روی یک تیر پرداختیم. از آنجایی که المانهای طولی یک تیر تنها در معرض کشش یا فشار قرار میگیرند، به منظور تعیین تنشهای ناشی از کرنشهای طولی میتوان از منحنی تنش-کرنش کمک گرفت. این تنشها معمولاً بر روی تمام سطح مقطع تیر اعمال میشوند. به علاوه، شدت آنها با توجه به شکل منحنی تنش-کرنش و ابعاد سطح مقطع تغییر میکند. در این مقاله، به معرفی نحوه ارزیابی تنش های نرمال موجود در تیرها خواهیم پرداخت. در انتها نیز به منظور آشنایی با کاربرد روابط ارائه شده، چند مثال کاربردی را تشریح خواهیم کرد.
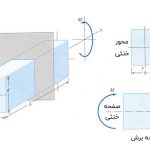
تنش نرمال
پرکاربردترین رابطه بین تنش و کرنش در مسائل مهندسی، معادله مورد استفاده برای مواد الاستیک خطی است. در این مواد، با ترکیب معادله قانون هوک برای تنش تک محوری و رابطه کرنش طولی تیر، رابطه زیر به دست میآید:

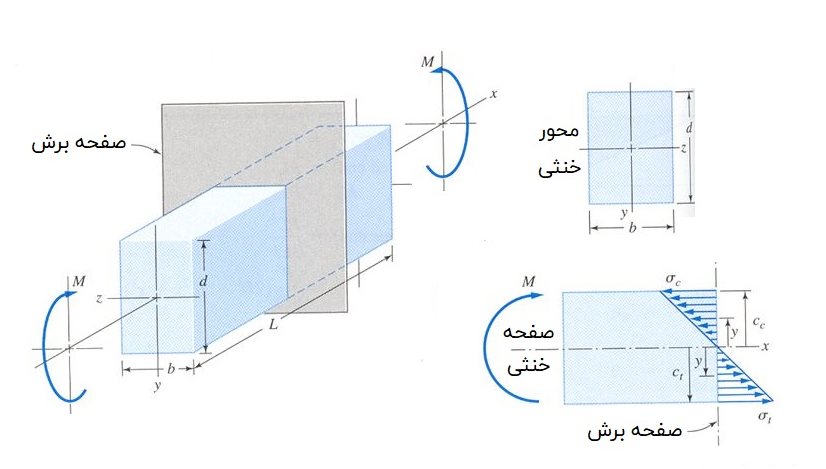
به این ترتیب، تنشهای نرمال اعمال شده بر روی سطح مقطع تیر با فاصله y از صفحه خنثی رابطه مستقیم دارند. شکل زیر، نحوه توزیع تنش بر اساس این رابطه را نمایش میدهد. در این مثال، گشتاور خمشی M دارای علامت مثبت و خمیدگی تیر دارای انحنای مثبت است.
در هنگام مثبت بودن انحنا، تنشهای σx در بالای صفحه خنثی دارای علامت منفی (از نوع فشاری) و در پایین این صفحه دارای علامت مثبت (از نوع کششی) خواهند بود. در شکل بالا، جهتگیری اعمال تنشهای فشاری به سمت داخل سطح مقطع و جهتگیری اعمال تنشهای کششی به سمت خارج سطح مقطع است.
به منظور تعیین محل رخ دادن مقدار مشخصی از تنش با توجه به رابطه ارائه شده در ابتدای این بخش، باید مبدأ دستگاه مختصات دربرگیرنده سطح مقطع را مشخص کنیم. این مبدأ بر روی محور خنثی مطابقت دارد. علاوه بر این، باید رابطه بین انحنا و گشتاور خمشی را نیز به دست بیاوریم و آن را در σx=-Eκy قرار دهیم. به این ترتیب، رابطه بین تنش و گشتاور خمشی مشخص میشود. شروع این فرآیند با تعیین برآیند تنشهای اعمال شده بر روی سطح مقطع تیر امکانپذیر خواهد شد.
به طور کلی، برآیند تنشهای نرمال داری دو مؤلفه است. مؤلفه اول، نیروی اعمال شده در راستای x و مؤلفه دوم، گشتاور خمشی حول محور z را نمایش میدهد. با این وجود، در صورت اعمال خمش خالص، مقدار نیروی محوری صفر خواهد بود. بنابراین، با در نظر داشتن نکات زیر میتوانیم دو معادله استاتیک را برای تحلیل مسئله به دست بیاوریم:
- مقدار برآیند نیرو در راستای x برابر با صفر است.
- مقدار برآیند گشتاور با گشتاور خمشی M برابری میکند.
با استفاده از معادله اول، مختصات محور خنثی و با به کارگیری معادله دوم، رابطه بین گشتاور خمشی و انحنا به دست میآید.
مختصات محور خنثی
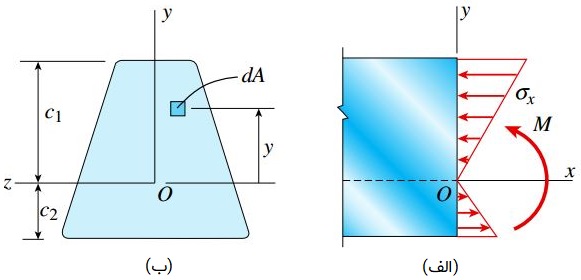
به منظور تعیین اولین معادله استاتیک، المان سطح dA را مطابق شکل زیر در نظر بگیرید. این المان در فاصله y از محور خنثی قرار دارد. از اینرو، تنش اعمال شده بر روی آن (σx) با استفاده از رابطه σx=-Eκy قابل محاسبه خواهد بود. نیروی وارد شده بر المان با σxdA برابر بوده و در هنگام مثبت بودن y به صورت فشاری است.

به دلیل عدم وجود برآیند نیرو بر روی مقطع عرضی، انتگرال σxdA در محدوده A برابر با صفر است:
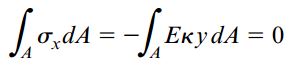
کمیتهای انحنا κ و مدول الاستیسیته E، دارای مقادیر ثابت و غیر صفر هستند. به همین دلیل میتوان آنها را از انتگرال بالا حذف کرد. به این ترتیب، خواهیم داشت:

این معادله بیان میکند که گشتاور اول سطح مقطع عرضی حول محور z برابر با صفر است. به عبارت دیگر، محور z از مرکز هندسی مقطع عرضی عبور میکند. محور z بر روی محور خنثی نیز منطبق است. بنابراین، اگر ماده از قانون هوک پیروی کند و هیچ نیروی محوری بر روی مقطع عرضی اعمال نشود، محور خنثی از مرکز هندسی سطح مقطع عبور خواهد کرد. بر اساس این مشاهدات، موقعیت قرارگیری محور خنثی به سادگی تعیین میشود. توجه داشته باشید که مطالب ارائه شده در این مقاله برای تیرهایی قابل استفاده است که مقاطع عرضی آنها نسبت به محور y دارای تقارن باشند. در نتیجه، مرکز مختصات O بر روی مرکز هندسی سطح مقطع قرار خواهد گرفت.
به دلیل تقارن مقاطع عرضی نسبت به محور y، این محور به عنوان یک «محور اصلی» (Principal Axis) محسوب میشود. محور z نیز به دلیل عمود بودن بر محور y، یکی دیگر از محورهای اصلی خواهد بود. از اینرو، در صورت اعمال خمش خالص بر روی یک تیر از جنس مواد الاستیک خطی، محورهای y و z به عنوان محورهای اصلی مرکزی در نظر گرفته خواهند شد.
رابطه بین گشتاور و انحنا
دومین معادله استاتیک بیان میکند که برآیند گشتاور تنشهای نرمال σx با گشتاور خمشی M برابر است. در صورت مثبت بودن σx، المان نیروی σxydA بر روی المان سطح dA دارای جهتگیری مثبت و در صورت منفی بودن σx، این المان دارای جهتگیری منفی خواهد بود.
به دلیل قرارگیری dA در بالای محور خنثی، تنش مثبت σx بر روی المان سطح اعمال میشود و یک المان گشتاور با مقدار σxydA را به وجود میآورد. این المان گشتاور در خلاف جهت گشتاور خمشی مثبت M عمل میکند.

با توجه به شکل بالا و مطالب ارائه شده، خواهیم داشت:
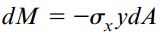
به این ترتیب، انتگرال تمام المانهای موجود بر روی سطح مقطع A باید با گشتاور خمشی M برابر باشد:
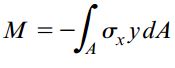
با جایگذاری σx=-Eκy در انتگرال بالا، به معادله زیر میرسیم:

این معادله، رابطه بین انحنای تیر و گشتاور خمشی را نمایش میدهد. از آنجایی که انتگرال موجود در معادله بالا به عنوان یکی از خواص سطح مقطع تیر در نظر گرفته میشود، بازنویسی این معادله به صورت زیر مناسبتر خواهد بود:

در این معادله:

این انتگرال با عنوان ممان اینرسی سطح مقطع نسبت محور z (محور خنثی) شناخته میشود. مقدار ممان اینرسی همیشه مثبت و واحد آن با طول به توان چهار برابر است. به عنوان مثال، به منظور تحلیل تیرها در سیستم SI، این کمیت با واحد mm4 و در سیستم یکاهای آمریکایی با واحد in4 مورد محاسبه قرار میگیرد. در صورت بازنویسی معادله M=κEI میتوانیم میزان انحنای تیر را بر حسب گشتاور خمشی تعیین کنیم:

رابطه بالا، «معادله گشتاور-انحنا» (Moment-Curvature Equation) نام دارد. این معادله نشان میدهد که انحنا با گشتاور خمشی M دارای رابطه مستقیم و با کمیت EI رابطه عکس دارد. EI با عنوان «صلبیت خمشی» (Flexural Rigidity) شناخته میشود. صلبیت خمشی معیاری برای نمایش مقاومت تیر در برابر خمش است. از اینرو، هر چه مقدار این کمیت بیشتر باشد، انحنای تیر برای یک گشتاور خمشی مشخص کمتر خواهد بود. در نهایت توجه داشته باشید که گشتاور خمشی مثبت باعث ایجاد انحنای مثبت و گشتاور خمشی منفی منجر به ایجاد انحنای منفی میشود (شکل زیر).
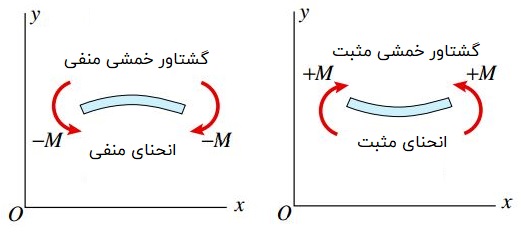
رابطه خمش
با تعیین محل قرارگیری محور خنثی و رابطه گشتاور-انحنا، امکان محاسبه تنشهای موجود در تیر بر اساس گشتاور خمشی فراهم میشود. اگر رابطه انحنا را در σx=-Eκy جایگذاری کنیم، به معادله زیر خواهیم رسید:

این معادله با عنوان «رابطه خمش» (Flexure Formula) شناخته میشود و رابطه مستقیم بین تنش با گشتاور خمشی و رابطه عکس بین تنش با ممان اینرسی سطح مقطع را نمایش میدهد. علاوه بر این، تنشهای موجود در تیر با تغییر فاصله y (فاصله از محور خنثی) به صورت خطی تغییر میکنند. تنشهای به دست آمده از رابطه خمش با عنوان «تنش خمشی» (Bending Stress یا Flexural Stress) شناخته میشوند.
در صورت مثبت بودن گشتاور خمشی تیر، تنشهای خمشی بر روی بخشی از سطح مقطع با فاصله منفی از محور خنثی دارای علامت مثبت (کششی) خواهند بود. این تنشها در بخش بالایی تیر با علامت منفی (فشاری) ظاهر میشوند. اگر علامت گشتاور خمشی منفی شود، علامت تنشها برعکس خواهد شد (شکل زیر).
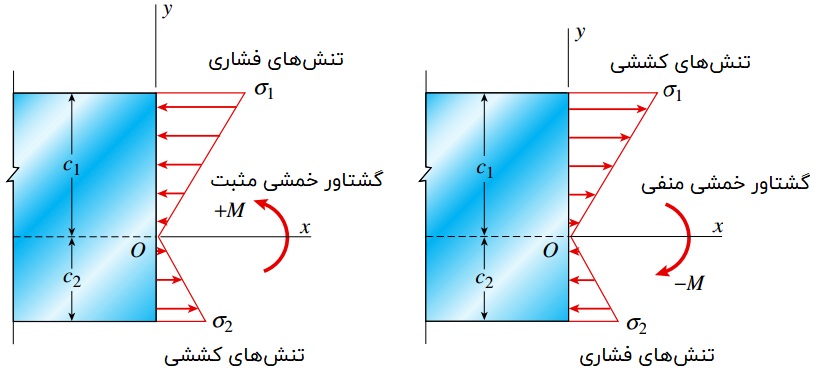
تنشهای ماکسیمم موجود روی سطح مقطع
تنشهای کششی و فشاری ماکسیمم موجود بر روی هر سطح مقطع دلخواه، در نقاطی با بیشترین فاصله از محور خنثی رخ میدهند. در شکل بالا، c1 و c2 به ترتیب فاصله محور خنثی از دورترین المانهای موجود در جهت منفی و مثبت هستند. به این ترتیب، تنشهای نرمال ماکسیمم بر روی این نقاط به صورت زیر خواهند بود:
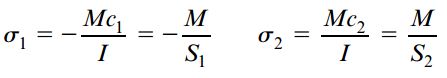
که در آنها:

کمیتهای S1 و S2 با عنوان «مدول مقطع» (Section Modulus) شناخته میشوند. با توجه به روابط بالا، مدول مقطع دارای واحد طول به توان سه (in3 یا mm3) است. علاوه بر این، توجه داشته باشید که فواصل c1 و c2 نسبت به بالا و پایین تیر همیشه مثبت در نظر گرفته میشوند.
شکلهای دارای تقارن مضاعف
اگر مقطع عرضی تیر علاوه بر محور z نسبت به محور y نیز تقارن داشته باشد (تقارن مضاعف)، رابطه c1=c2=c برقرار خواهد بود. به این ترتیب، تنشهای کششی یا فشاری ماکسیمم با استفاده از رابطه زیر به دست میآیند:

که در آن:
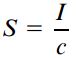
در این حالت، کمیت S تنها مدول مقطع برای سطح مورد بررسی خواهد بود. اگر تیر دارای سطح مقطع مستطیلی با عرض b و ارتفاع h باشد (شکل زیر)، ممان اینرسی و مدول مقطع با کمک روابط زیر تعیین می شوند:
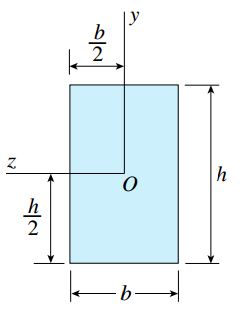
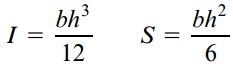
ممان اینرسی و مدول مقطع برای یک سطح مقطع دایرهای با قطر d (مانند شکل زیر) نیز با استفاده از روابط زیر به دست میآیند:

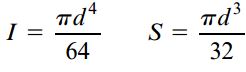
برای دیگر شکلهای دارای تقارن مضاعف نظیر لولههای توخالی (دایرهای یا مستطیلی) و «بال پهن» (Wide Flange) نیز می توان از طریق روابط بالا به منظور تعیین خواص سطح مقطع استفاده کرد.
نکات تکمیلی
مطالب ارائه شده در این مقاله برای حالت خمش خالص تیرهای منشوری (دارای سطح مقطع یکنواخت در راستای محور طولی) و همگن (یکسان بودن خواص مواد تشکیلدهنده در تمام نقاط) با رفتار الاستیک خطی قابل استفاده است. در صورت اعمال خمش غیر یکنواخت بر روی یک تیر، نیروهای برشی باعث ایجاد «تاب خوردگی» (Warping) در مقاطع عرضی خواهد شد. در این حالت، نقاط سطح مقطعی که پیش از اعمال خمش بر روی یک صفحه قرار داشتند، پس از بارگذاری بر روی یک صفحه مشترک قرار نخواهند داشت.
تاب خوردگی ناشی از تغییر شکلهای برشی، رفتار تیر را بسیار پیچیده میکند. با این وجود، برخی از تحقیقات نشان میدهند که در حضور تنشهای برشی و تاب خوردگی همراه آنها، مقدار تنشهای نرمال به دست آمده از رابطه پیچش با تغییر چندانی مواجه نمیشود. از اینرو، به کارگیری روابط ارائه شده در این مقاله برای محاسبه تنشهای نرمال در تیرهای تحت خمش غیر یکنواخت نیز قابل توجیه است.
مثالها
در این بخش، به منظور آشنایی بهتر با روابط ارائه شده و نحوه به کارگیری آنها در تحلیل تیرهای تحت پیچش خالص، به تشریح کامل سه مثال خواهیم پرداخت. توجه داشته باشید که برای حل مثالهای 2 و 3، از مفاهیم نیروی برشی و گشتاور خمشی و نمودارهای مربوط به آنها استفاده شده است.
مثال 1
میلهای ساخته شده از فولاد مقاوم با قطر d مطابق شکل زیر در اطراف استوانهای با شعاع R0 خم شده است. اگر قطر این میله d=4mm، شعاع استوانه R0=0.5m، مدول الاستیسیته فولاد E=200GPa و حد الاستیک آن σp1=1200MPa در نظر گرفته شود، گشتاور خمشی M و تنش خمشی ماکسیمم σmax چقدر خواهد بود؟
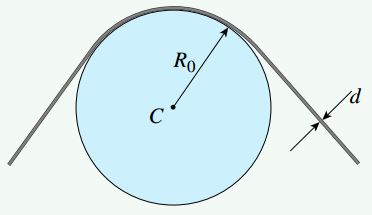
اولین قدم برای حل این مسئله، تعیین شعاع انحنای ρ میله خمیده است. با مشخص شدن این پارامتر، گشتاور خمشی میتوان گشتاور خمشی و تنشهای ماکسیمم را مورد محاسبه قرار داد.
شعاع انحنا
در این مثال، شعاع انحنای میله خمیده با فاصله مرکز استوانه تا محور خنثی سطح مقطع میله برابری میکند:
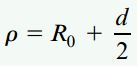
گشتاور خمشی
گشتاور خمشی موجود در میله با استفاده از رابطه گشتاور-انحنا به دست میآید:
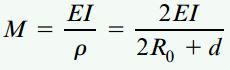
I در این رابطه، ممان اینرسی سطح مقطع عرضی میله را نمایش میدهد. با جایگذاری I=πd4/64 در رابطه بالا خواهیم داشت:
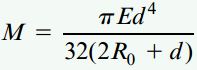
به دلیل واضح بودن جهتگیری خمش در شکل مسئله، رابطه بالا بدون در نظر گرفتن علامت گشتاور خمشی به دست آمد.
تنشهای خمشی ماکسیمم
تنشهای کششی و فشاری ماکسیمم که از نظر عددی با هم برابر هستند، از طریق رابطه خمش محاسبه میشوند:

در رابطه بالا، S بیانگر مدول مقطع یک سطح دایرهای است. با جایگذاری عبارتهای M از بخش قبلی و S=πd3/32 خواهیم داشت:
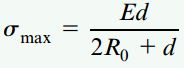
در صورت قرار دادن y=d/2 در رابطه σx=-Eκy، بازنویسی این رابطه بر حسب d/2 و جایگذاری آن در معادله به دست آمده برای تعیین شعاع انحنا ρ (بخش اول حل مسئله) نیز به نتیجه مشابهی دست خواهیم یافت. بررسی شکل زیر نشان میدهد که تنشهای به وجود آمده در بخش پایینی میله از نوع فشاری و در بخش بالایی آن از نوع کششی هستند.
نتایج عددی
اکنون میتوانیم با قرار دادن مقادیر عددی هر یک از کمیتها درون روابط به دست آمده در بخشهای قبلی، گشتاور خمشی و تنش خمشی ماکسیمم اعمال شده بر میله را محاسبه کنم:
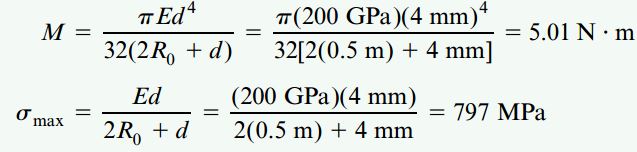
با توجه به نتایج به دست آمده، تنش ماکسیمم σx کمتر از حد تناسب فولاد به کار رفته در میله است. به همین دلیل، محاسبات صورت گرفته دارای اعتبار هستند. توجه داشته باشید که به دلیل طول زیاد شعاع استوانه نسبت به قطر میله، صرف نظر کردن از پارامتر d در مخرج روابط بالا مانعی ندارد. با این کار، مقادیر M و σx به صورت زیر خواهند بود:

نتایج بالا نسبت به نتایج به دست آمده از روابط قبلی محافظهکارانهتر و دارای اختلاف تقریباً 1 درصدی هستند.
مثال 2
شکل زیر، یک تیر ساده با انتهای آزاد با عرض مقطع b=5in و ارتفاع h=22in را نمایش میدهد که در معرض بار گسترده یکنواخت با شدت q=400lb/ft و بار متمرکز P=2400lb قرار دارد. بار یکنواخت q، وزن تیر را نیز شامل میشود. این تیر از چوب روکشدار و چسب مخصوص ساخت و ساز تشکیل شده است. با توجه به پیکربندی سازه و اطلاعات مسئله:
- الف: تنشهای کششی و فشاری ماکسیمم ناشی از خمش را محاسبه کنید.
- ب: با فرض ثابت بودن بار q و تنش نرمال مجاز σa=1875psi (در بارگذاری کششی و فشاری)، حداکثر مقدار مجاز بار P را به دست بیاورید.

الف: تنشهای نرمال ماکسیمم
به منظور شروع تحلیل این مسئله، نمودارهای نیروی برشی و گشتاور خمشی پیکربندی بالا را رسم میکنیم. سپس، گشتاور خمشی ماکسیمم را به دست میآوریم. با توجه به وضعیت بارگذاری این تیر، گشتاور ماکسیمم در زیر محل اعمال بار متمرکز رخ میدهد (در مثال 3 از مبحث رسم نمودار نیروی برشی و گشتاور خمشی این موضوع به طور مفصل مورد بررسی قرار گرفته است).
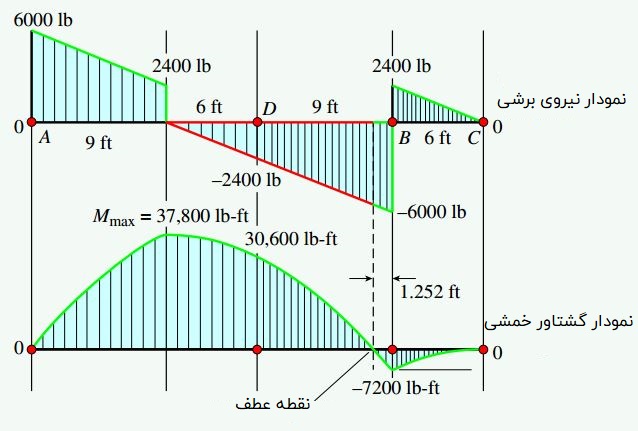
بر اساس نمودار گشتاور خمشی، Mmax در فاصله 9 فوتی از تکیهگاه A برابر با 37800lb-ft است. توجه داشته باشید که تنش خمشی ماکسیمم در مقطع دربرگیرنده گشتاور ماکسیمم رخ میدهد.
مدول مقطع
مدول مقطع سطح مستطیلی تیر با استفاده از رابطه زیر به دست میآید:
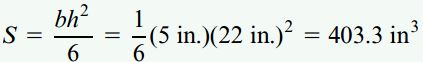
تنشهای ماکسیمم
تنشهای کششی و فشاری ماکسیمم نیز از طریق روابط زیر محاسبه میشوند:

نمودار گشتاور خمشی در این مثال با توجه به بخش تحت فشار تیر رسم شده است. از اینرو، بخش زیادی از بالای تیر در معرض تنش فشاری و بخش زیادی از پایین تیر در معرض تنش کششی قرار دارد. برعکس این موضوع برای بخش BC صادق است.
ب: حداکثر مقدار مجاز بار P
مقدار تنشهای نرمال موجود در محل رخ دادن گشتاور خمشی ماکسیمم بسیار کمتر از مقدار مجاز (σa=1875psi) است. در نتیجه، تیر مورد بررسی میتواند مقادیر بسیار بزرگتری نسبت به بار متمرکز P در بخش الف مسئله را تحمل کند. اگر فاصله P تا تکیهگاه A را a=9ft، طول محدوده AB را L=24ft و بار گسترده را با شدت ثابت q=400lb/ft در نظر بگیریم، عکسالعمل تکیهگاهی در نقطه A به صورت زیر خواهد بود:
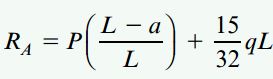
گشتاور ماکسیمم در فاصله a از تکیهگاه A رخ میدهد و رابطه آن به صورت زیر نوشته میشود:
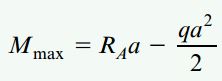
با برابر قرار دادن Mmax با σa)(S)=63016lb-ft) و جایگذاری این مقدار در رابطه RA، مقدار عددی Pmax=6883lb به دست میآید.
راه حل دیگر
مقدار گشتاور ماکسیمم بر روی نمودار برابر با 37800lb-ft و مقدار گشتاور ماکسیمم با در نظر گرفتن تنش مجاز σa برابر با 63016lb-ft است. اختلاف این دو با Δm=25216lb-ft نمایش داده میشود. به این ترتیب، مقدار بار اضافی مورد نیاز برای رسیدن به گشتاور خمشی ماکسیمم در قسمت ب مسئله از رابطه زیر به دست میآید:
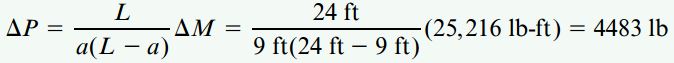
اگر ΔP را به P=2400lb در بخش الف اضافه کنیم، خواهیم داشت:
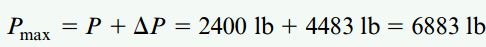
توجه داشته باشید که حداکثر بار مجاز P باعث ایجاد تنشهای نرمال مجاز در محل رخ دادن گشتاور ماکسیمم میشود. اگر Pmax را در رابطه RA قرار دهیم، RA=8802lb و Mmax=63016lb-ft خواهد شد. با استفاده از این مقادیر، تنشهای موجود در نقطه اعمال Pmax به صورت زیر خواهند بود:
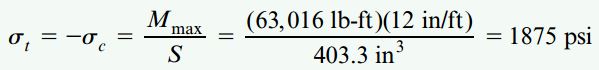
مثال 3
شکل زیر، یک تیر ساده با انتهای آزاد را نمایش میدهد که تمام طول آن در معرض یک بار گسترده یکنواخت با شدت q=3.2kN/m قرار دارد. طول بخش ساده L=3m، طول بخش آزاد L/2=1.5m و سطح مقطع تیر به شکل کانالی با عرض b=300mm و ارتفاع h=80mm است. ضخامت جانِ تیر با مقدار t=12mm و ضخامت میانگین ضخامت بالها یا فلنجها نیز با همین مقدار برابری میکند.
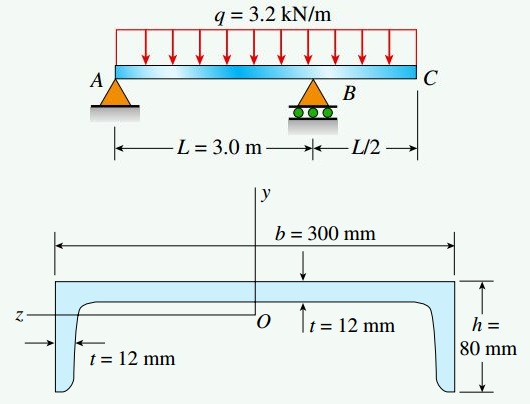
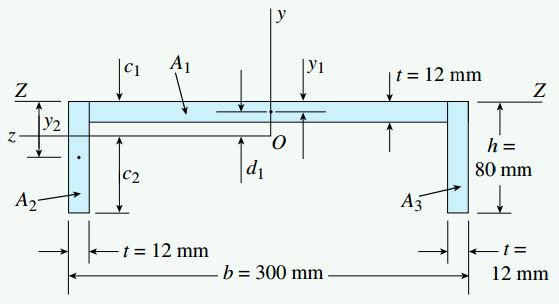
به منظور محاسبه خواص مقطع عرضی تیر، آن را به صورت یک سطح متشکل از سه مستطیل در نظر بگیرید (شکل زیر).
- الف: تنشهای کششی و فشاری ماکسیمم ناشی از اعمال بار یکنواخت را به دست بیاورید.
- ب: حداکثر مقدار مجاز بار یکنواخت q را با در نظر گرفتن تنش مجاز کششی σaT=110MPa و تنش مجاز فشاری σaC=92MPa محاسبه کنید.
الف: تنشهای کششی و فشاری ماکسیمم
در مرحله اول تحلیل باید عکسالعملهای تکیهگاهی، نیروهای برشی و گشتاورهای خمشی مورد محاسبه قرار دهیم. به این ترتیب، عکسالعملهای موجود در تکیهگاههای A و B را مطابق مطالب ارائه شده در مبحث «مثالهای کاربردی تعیین عکسالعملهای تکیهگاهی تیرها» تعیین میکنیم. نتایج به دست آمده به صورت زیر خواهند بود:
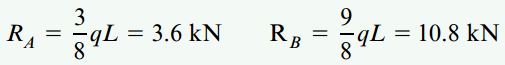
با توجه به مقادیر به دست آمده، نمودار نیروی برشی تیر را مطابق شکل زیر رسم میکنیم. توجه داشته باشید که نیروی برشی در این مثال در دو نقطه تغییر علامت میدهد و مقدار آن برابر با صفر میشود. نقطه اول در فاصله 1.125 متری از تکیهگاه سمت چپ و نقطه دوم بر روی تکیهگاه سمت راست قرار دارد.
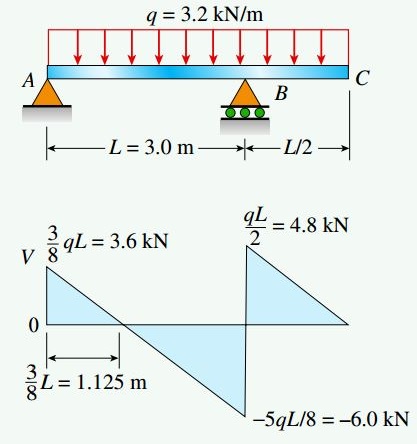
در مرحله بعد، نمودار گشتاور خمشی تیر را مطابق شکل زیر رسم میکنیم. گشتاورهای خمشی ماکسیمم و منفی بر روی محل تغییر علامت نیروی برشی رخ میدهند.

مقادیر گشتاورهای ماکسیمم از روابط زیر به دست میآیند:
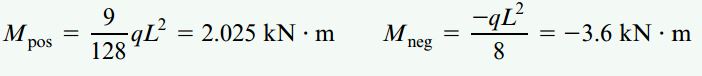
مختصات محور خنثی سطح مقطع
مبدأ مختصات y-z بر روی مرکز هندسی سطح مقطع قرار گرفته است. از اینرو، محور z به عنوان محور خنثی سطح مقطع در نظر گرفته میشود.

موقعیت قرارگیری مرکز هندسی شکل بالا به صورت زیر به دست میآید:
- تقسیم سطح مقطع تیر به سه مستطیل A2 ،A1 و A3
- رسم خط مرجع Z-Z بر روی لبه بالایی سطح مقطع
- در نظر گرفتن y1 و y2 به عنوان فاصله عمودی محور Z-Z تا مرکز سطح A1 و A2
به این ترتیب، محاسبات مورد نیاز برای تعیین محل قرارگیری مرکز هندسی کل سطح مقطع (c1 و c2) به صورت زیر خواهد بود:

ممان اینرسی
به منظور محاسبه تنشهای موجود در تیر بر اساس رابطه خمش باید در ابتدا ممان اینرسی سطح مقطع را با توجه به محور خنثی آن تعیین کنیم. برای انجام این محاسبات از قضیه محورهای موازی کمک میگیریم. ممان اینرسی سطح A1 از رابطه زیر به دست میآید:
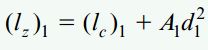
Ic)1) در رابطه بالا، ممان اینرسی سطح A1 حول محور مرکزی خودش و d1، فاصله محور مرکزی این سطح تا محور z را نمایش میدهد:
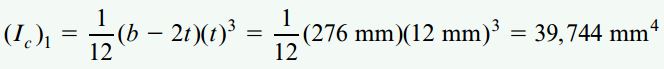

به این ترتیب، ممان اینرسی سطح A1 حول محور z برابر است با:
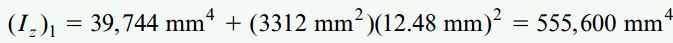
با همین روش، ممان اینرسی سطوح A2 و A3 نیز قابل محاسبه خواهد بود:

ممان اینرسی مرکزی Iz سطح مقطع نیز به صورت زیر به دست میآید:

مدول مقطع
مدول مقطع برای بخش بالایی و پایینی تیر به صورت زیر تعیین میشود:

اکنون با مشخص شدن ممان اینرسی و مدول مقطع سطح میتوانیم تنشهای ماکسیمم را به دست بیاوریم.
تنشهای ماکسیمم
در محل اعمال گشتاور خمشی ماکسیمم مثبت، حداکثر مقدار تنش کششی (σ2) در پایین تیر و حداکثر مقدار تنش فشاری (σ1) در بالای تیر رخ میدهد. بنابراین، با توجه به روابط ارائه شده در متن مقاله خواهیم داشت:

به همین ترتیب، حداکثر مقدار تنشهای موجود در محل رخ دادن گشتاور خمشی ماکسیمم منفی برابرند با:

با مقایسه مقادیر به دست آمده میتوان مشاهده کرد که تنش کششی ماکسیمم در تیر برابر با 50.5 مگا پاسکال است. این تنش بر روی بخش پایینی تیر و در محل اعمال گشتاور خمشی ماکسیمم مثبت رخ میدهد:

مقدار تنش فشاری ماکسیمم نیز با 89.8- مگا پاسکال برابری میکند. محل رخ دادن این تنش بر روی بخش بالایی تیر در محل اعمال گشتاور خمشی ماکسیمم منفی مشاهده میشود:
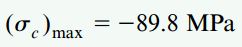
به خاطر داشته باشید که این تنشهای خمشی ماکسیمم بر اثر اعمال بار گسترده یکنواخت بر روی تیر به وجود آمدهاند.
ب: حداکثر مقدار مجاز بار یکنواخت q
در مرحله دوم تحلیل، میزان qmax را با توجه مقادیر مجاز تنشهای نرمال کششی و فشاری تعیین میکنیم. مقدار مجاز تنش فشاری σaC کمتر از این مقدار برای تنش کششی σaT است. این مقادیر برای بررسی احتمال رخ دادن کمانش محلی بالهای C شکل تیر در هنگام اعمال بارگذاری فشاری در نظر گرفته شدهاند.
به منظور انجام محاسبات در این بخش، رابطه خمش را برای تعیین مقادیر احتمالی qmax در چهار نقطه مورد استفاده قرار میدهیم (بالا و پایین تیر در محل رخ دادن گشتاور خمشی ماکسیمم مثبت Mpos، بالا و پایین تیر در محل رخ دادن گشتاور خمشی ماکسیمم منفی Mneg). برای هر یک از این نقاط، باید مقادیر مناسب تنش مجاز را به کار بگیریم. اگر جهتگیری تیر C شکل به صورت زیر باشد، بخش بالایی در محل اعمال Mpos تحت فشار و بخش پایینی تحت کشش قرار خواهد گرفت. این وضعیت برای نقطه B (محل اعمال Mneg) به صورت برعکس خواهد بود.

اکنون باید با استفاده از روابط Mpos و Mneg و برابر قرار دادن آنها با حاصلضرب مدول مقطع در تنش مجاز مربوطه، مقادیر احتمالی qmax را تعیین کنیم. در بخش AB بر روی تیر داریم:
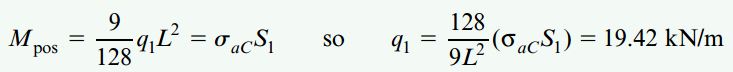
برای بخش AB زیر تیر خواهیم داشت:

در بخش بالایی مفصل B داریم:
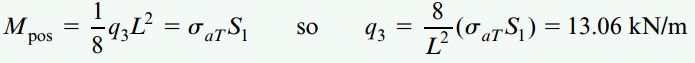
برای بخش پایینی مفصل B نیز خواهیم داشت:
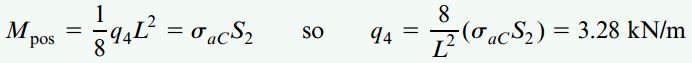
با توجه به این نتایج، بخش پایینی تیر در نزدیکی مفصل B (اعمال فشار به نوک بالهای تیر) حداکثر مقدار مجاز بار یکنواخت q را کنترل میکند. به این ترتیب:
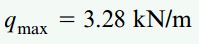
^^












