بارگذاری ضربه ای و رفتار مواد در شرایط بارگذاری دینامیک

نحوه اعمال بار به مواد مختلف را می‌توان به دو گروه «بارگذاری استاتیک» (Static Loading) و «بارگذاری دینامیک» (Dynamic Loading) تقسیم‌بندی کرد. یکی از معیارهای تشخیص نوع بارگذاری، ثابت یا متغیر بودن بار در طی زمان است. در بارگذاری استاتیک، بار به آرامی بر روی سازه اعمال می‌شود و هیچ لرزشی درون سیستم رخ نمی‌دهد. در این شرایط، میزان بار به تدریج از 0 تا حداکثر مقدار مورد نظر افزایش می‌یابد و سپس در همان مقدار حداکثری ثابت باقی می‌ماند.

شرایط بارگذاری دینامیک با بارگذاری استاتیک متفاوت است. این نوع بارگذاری انواع مختلفی دارد. در برخی از موارد، اعمال بار برای دوره‌های طولانی‌مدت صورت می‌گیرد و شدت آن به طور پیوسته تغییر می‌کند. به بارهای اعمال شد در این شرایط، «بارهای متناوب» (Fluctuating Loads) گفته می‌شود. بارهای متناوب توسط ماشین‌آلات چرخشی، ترافیک، تندباد، امواج آب، زلزله و فرآیندهای تولید قطعات به وجود می‌آیند. در نوع دیگر بارگذاری دینامیک، اعمال بار و توقف آن به صورت ناگهانی صورت می‌گیرد. به بارهای اعمال شده در این شرایط، «بارهای ضربه‌ای» (Impact Loads) گفته می‌شود. بارهای ضربه‌ای در هنگام برخورد دو شی به یکدیگر یا اصابت یک شی در حال سقوط به یک سازه ایجاد می‌شوند. در این مقاله، به معرفی بارهای ضربه‌ای و مفاهیم مرتبط با آن خواهیم پرداخت. در انتها نیز چند مثال کاربردی را برای شما تشریح خواهیم کرد.

بارگذاری ضربه‌ای

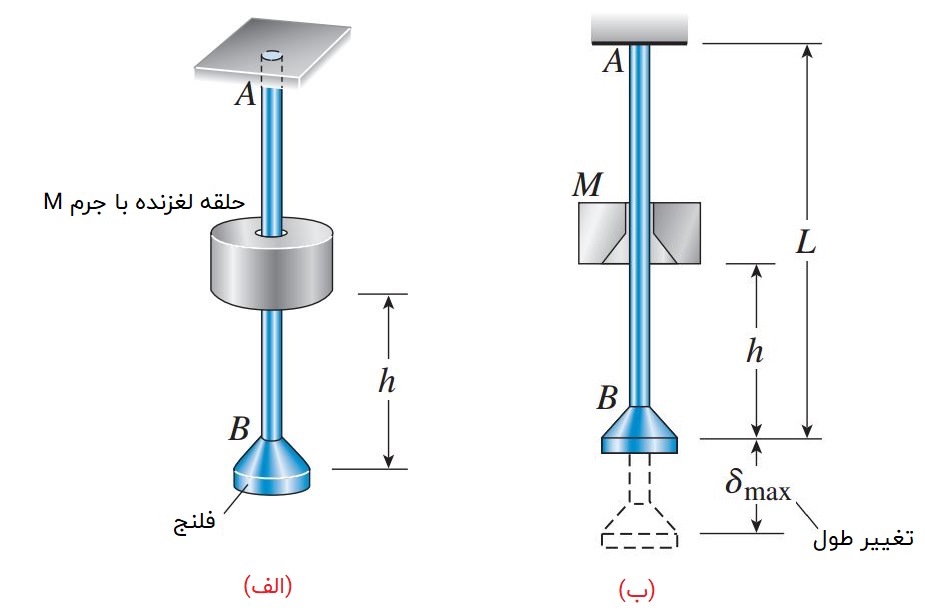
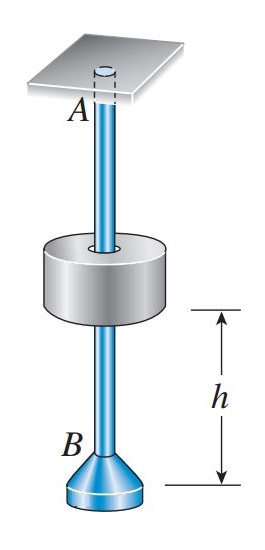
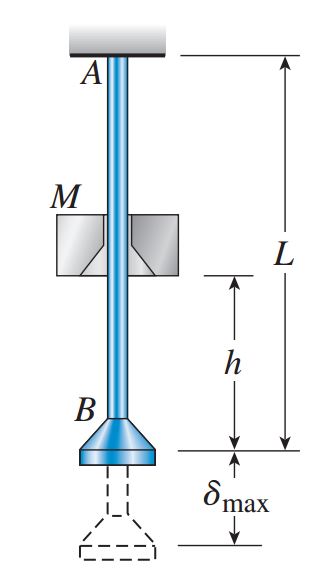
برای درک نحوه واکنش سازه‌ها در هنگام اعمال بارهای ضربه‌ای، فرآیند اصابت یک شی در حال سقوط به انتهای یک میله منشوری را مورد بررسی قرار می‌دهیم (شکل زیر). در این فرآیند، حلقه M که در حالت سکون قرار دارد، از ارتفاع h بر روی فلنج موجود در انتهای میله AB سقوط می‌کند. هنگام اصابت حلقه به فلنج، طول میله افزایش می‌یابد و منجر به ایجاد تنش‌های محوری درون میله می‌شود.

در یک بازه زمانی بسیار کوتاه (در حدود چند میلی‌ثانیه)، فلنج به سمت پایین حرکت می‌کند و به موقعیت حداکثر جابجایی خود (δ_max) می‌رسد. پس از این لحظه، با ایجاد لرزش طولی در میله و حرکت آن در جهت بالا و پایین، طول میله کاهش، سپس افزایش و دوباره کاهش می‌یابد. این لرزش مشابه لرزش ایجاد شده در هنگام کشیدن و رها کردن یک فنر یا جابجایی‌های یک فرد در حین انجام بانجی جامپینگ است. پس از مدت کوتاهی، این لرزش‌ها به دلیل وجود اثرات میرایی متوقف می‌شوند و با قرارگیری حلقه بر روی فلنج، میله به حالت سکون بازمی‌گردد.

واکنش میله به حلقه در حال سقوط بسیار پیچیده است. به همین دلیل، به منظور اجرای یک تحلیل دقیق و کامل بر روی این فرآیند باید از روش‌های پیشرفته ریاضی کمک گرفت. اگرچه، با استفاده از مفهوم انرژی کرنشی و در نظر گرفتن فرضیات ساده‌سازی می‌توان واکنش این میله به بارگذاری ضربه‌ای را به صورت تقریبی مورد ارزیابی قرار داد.

برای شروع تحلیل، انرژی سیستم پیش از رهاسازی حلقه را در نظر بگیرید. انرژی پتانسیل حلقه نسبت به ارتفاع فلنج برابر Mgh است. پارامتر g، شتاب جاذبه زمین (9.81 متر بر مجذور ثانیه) را نمایش می‌دهد. با سقوط حلقه، انرژی پتانسیل به انرژی جنبشی تبدیل می‌شود. در لحظه اصابت حلقه به فلنج، انرژی پتانسیل آن به صفر و انرژی جنبشی آن به Mv²/2 می‌رسد. که در این رابطه، v برابر سرعت حلقه در لحظه اصابت با فلنج است و مقدار آن از طریق عبارت ^0.5(2gh) به دست می‌آید.

پس از لحظه اصابت، انرژی جنبشی حلقه به شکل‌های دیگر انرژی تبدیل خواهد شد. بخشی از انرژی جنبشی، به انرژی کرنشی میله کشیده شده تبدیل می‌شود. یک بخش دیگر از این انرژی به صورت گرما و تغییر شکل پلاستیک در ناحیه اصابت حلقه به فلنج هدر می‌رود. بخش کوچکی از آن نیز به صورت انرژی جنبشی باقی می‌ماند. انرژی جنبشی باقیمانده یا باعث حرکت بیشتر حلقه در جهت پایین می‌شود یا حلقه را به مقدار کمی در جهت بالا پرتاب می‌کند.

به منظور اجرای یک تحلیل ساده بر روی این شرایط پیچیده، فرضیات زیر را در نظر می‌گیریم:

• حلقه و فلنج به گونه‌ای هستند که در هنگام اصابت، حلقه به فلنج می‌چسبد و با آن به سمت پایین حرکت می‌کند. به عبارت دیگر، حلقه در لحظه اصابت به فلنج، هیچ حرکت رو به بالایی نخواهد داشت. اگر جرم حلقه نسبت به جرم میله بزرگ باشد، احتمال وقوع این رفتار وجود دارد.
• هیچ هدر رفت انرژی در طی این فرآیند رخ نمی‌دهد و تمام انرژی جنبشی به انرژی کرنشی تبدیل می‌شود. تنش‌های محاسبه شده در این حالت بیشتر از تنش‌ها در حالتی است که هدر رفت انرژی در آن در نظر گرفته می‌شود.
• هیچ تغییری در انرژی پتانسیل میله رخ نمی‌دهد. به علاوه، انرژی کرنشی حاصل از وزن میله نیز نادیده گرفته می‌شود. این فرضیات تأثیر بسیار کمی بر روی نتایج به دست آمده دارند.
• تغییرات تنش‌های درون میله در ناحیه الاستیک خطی قرار دارند.
• توزیع تنش در این شرایط با توزیع تنش در شرایط اعمال یک بار استاتیک در انتهای پایینی میله یکسان است. به عبارت دیگر، توزیع تنش در سراسر میله به صورت یکنواخت خواهد بود. در واقعیت، موج‌های تنشی درون میله حرکت می‌کنند و باعث ایجاد تغییرات در توزیع تنش می‌شوند.

بر اساس فرضیات بالا، امکان محاسبه تغییر طول ماکسیمم و تنش‌های کششی ماکسیمم در بارگذاری ضربه‌ای فراهم می‌شود. در ادامه به توضیح نحوه محاسبه این پارامترها می‌پردازیم.

تغییر طول ماکسیمم

میزان تغییر طول ماکسیمم (δ_max) با استفاده از قواعد تبدیل انرژی تعیین می‌شود. به این منظور باید انرژی پتانسیل از دست رفته در هنگام سقوط حلقه را برابر با انرژی کرنشی ماکسیمم جذب‌شده توسط میله قرار داد. انرژی پتانسیل از دست رفته برابر است با:

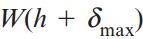
W: وزن حلقه است که از رابطه Mg به دست می‌آید؛ h+δ_max: مسیری که حلقه آن را طی می‌کند.

انرژی کرنشی میله برابر است با:

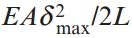
EA: صلبیت محوری؛ L: طول میله

اکنون روابط بالا را برابر هم قرار می‌دهیم:

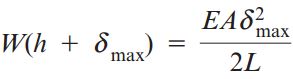
با بازنویسی معادله بالا و حل آن نسبت به ریشه مثبت δ_max خواهیم داشت:

توجه داشته باشید که در صورت افزایش طول میله (طول سقوط) و یا افزایش وزن حلقه، تغییر طول ماکسیمم نیز افزایش خواهد یافت. در صورت کاهش سختی (EA/L)، تغییر طول کاهش می‌یابد.

معادله بالا را می‌توان به شکل ساده‌تر بازنویسی کرد:

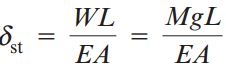
δ_st: تغییر طول میله در اثر وزن حلقه تحت شرایط بارگذاری استاتیک

اکنون می‌توانیم روابط δ_max را به صورت زیر بازنویسی کنیم:

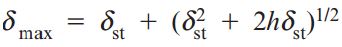
یا

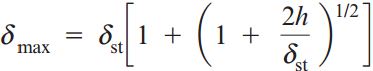
بر اساس رابطه بالا می‌توان مشاهده کرد که با اعمال یک بار هم‌اندازه، تغییر طول میله در شرایط بارگذاری ضربه‌ای بسیار بزرگ‌تر از تغییر طول در شرایط بارگذاری استاتیک است. به عنوان مثال، اگر ارتفاع h چهل برابر جابجایی استاتیک (δ_st) باشد، تغییر طول دینامیک، ده برابر تغییر طول استاتیک خواهد بود.

در صورتی که ارتفاع h نسبت تغییر طول استاتیک بزرگ باشد، می‌توان از اعداد 1 در رابطه بالا صرف نظر کرد. به این ترتیب خواهیم داشت:

که در آن:

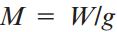
و

تنش ماکسیمم

مقدار تنش ماکسیمم (σ_max) در بارگذاری ضربه‌ای را می‌توان با استفاده از تغییر طول ماکسیمم به سادگی محاسبه کرد. به این ترتیب، بر اساس فرض یکنواخت بودن توزیع تنش در طول میله داریم:

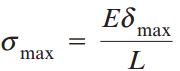
با جایگذاری رابطه بالا در رابطه تغییر طول ماکسیمم خواهیم داشت:

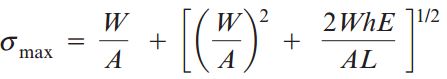
رابطه بالا را می‌توانیم برای شرایط بارگذاری استاتیک بازنویسی کنیم:

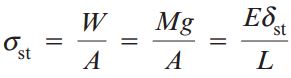
σ_st: تنش به وجود آمده در هنگام اعمال بار استاتیک

به این ترتیب، روابط تنش ماکسیمم به صورت زیر خواهد بود:

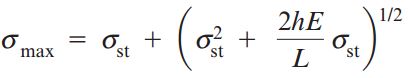
یا

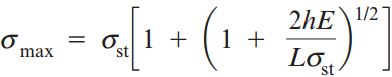
این رابطه نیز مانند رابطه δ_max نشان می‌دهد که در صورت اعمال بارهای برابر، تأثیر بارگذاری ضربه‌ای بر روی میزان تنش‌های به وجود آمده بسیار بیشتر از تأثیر بارگذاری استاتیک است. اگر ارتفاع h نسبت به میزان کشیدگی میله بزرگ باشد، می‌توانیم مقادیر 1 را از درون معادله بالا حذف کنیم:

بر اساس این رابطه، افزایش انرژی جنبشی (Mv²/2) باعث افزایش میزان تنش و افزایش حجم میله (AL) باعث کاهش میزان تنش می‌شود. به این ترتیب، در بارگذاری ضربه‌ای بر خلاف بارگذاری استاتیک، میزان تنش به طول میله (L) و مدول الاستیسیته (E) نیز بستگی دارد.

معادلات ارائه شده برای δ_max و σ_max تنها برای لحظه رسیدن فلنج به پایین‌ترین موقعیت قابل استفاده هستند. پس از رسیدن به تغییر طول ماکسیمم، میله در راستای محور خود می‌لرزد. این ارزش تا ثابت شدن میله در تغییر طول استاتیک ادامه می‌یابد. از این لحظه به بعد، مقادیر تنش و تغییر طول میله را می‌توان با استفاده از روابط δ_max و σ_max محاسبه کرد.

با وجود تعیین روابط δ_max و σ_max برای یک میله منشوری، این روابط برای تمام سازه‌های الاستیک خطی در شرایط بارگذاری ضربه‌ای قابل استفاده هستند. به منظور، باید به جای عبارت EA/L در روابط مذکور از مقدار سختی سازه مورد تحلیل استفاده کرد.

ضریب ضربه

عکس‌العمل دینامیکی یک سازه نسبت به عکس‌العمل استاتیکی آن با عنوان «ضریب ضربه» (Impact Factor) شناخته می‌شود. به عنوان مثال، ضریب ضربه برای تغییر طول میله نمایش داده شده در شکل زیر، نسبت تغییر طول ماکسیمم به تغییر طول استاتیک است:

δ_max: تغییر طول ماکسیمم؛ δ_st: تغییر طول استاتیک

این ضریب بیانگر تشدید میزان تغییر طول استاتیک در اثر اعمال بارگذاری ضربه‌ای است. رابطه ضریب ضربه برای تنش‌های موجود در یک میله نیز مشابه رابطه بالا نوشته می‌شود (نسبت σ_max به σ_st). اگر حلقه در حال سقوط دارای ارتفاع قابل توجهی باشد، ضریب ضربه نیز بسیار بزرگ خواهد بود (مقداری نظیر 100 یا بیشتر).

بارگذاری ناگهانی

یکی از حالت‌های خاص بارگذاری ضربه‌ای، در هنگام اعمال ناگهانی بار بدون سرعت اولیه رخ می‌دهد. برای توصیف این نوع بارگذاری، میله منشوری زیر را در نظر بگیرید. فرض کنید که ارتفاع حلقه تا لحظه قرارگیری آن بر روی فلنج به آرامی کاهش داده شود.

در صورت رها کردن ناگهانی حلقه در لحظه تماس با فلنج، «بارگذاری ناگهانی» (Suddenly Applied Load) رخ می‌دهد. علیرغم عدم وجود انرژی جنبشی در لحظه شروع این نوع اعمال بار، رفتار بارگذاری ناگهانی با بارگذاری استاتیک کاملاً متفاوت است. در بارگذاری استاتیک، بار به تدریج رها می‌شود و همیشه بین بار اعمال شده و نیروی مقاوم میله شرایط تعادل برقرار است.

اکنون رفتار میله در هنگام رهاسازی ناگهانی حلقه در نقطه تماس با فلنج را مورد تحلیل قرار می‌دهیم. میزان تنش و تغییر طول میله در شروع بارگذاری صفر است. در این لحظه، حلقه تحت نیروی وزن خود به سمت پایین حرکت می‌کند. در طی این حرکت، میله تحت کشش قرار می‌گیرد و میزان نیروی مقاوم آن به تدریج افزایش می‌یابد. حرکت حلقه تا لحظه تعادل بین نیروی مقاوم با وزن آن (W) ادامه پیدا می‌کند. در این لحظه بخصوص، میزان تغییر طول میله برابر با δ_st است. پس از طی کردن مسیر δ_st، مقداری انرژی جنبشی در حلقه به وجود می‌آید. بنابراین، حرکت رو به پایین حلقه تا رسیدن سرعت آن به مقدار صفر ادامه می‌یابد. اگر ارتفاع h را برابر با صفر قرار دهیم، رابطه تغییر طول ماکسیمم برای این شرایط به صورت زیر خواهد بود:

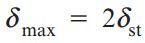
بر اساس رابطه بالا می‌توان مشاهده کرد که در صورت اعمال بارهای یکسان، تغییر طول ناشی از بارگذاری ناگهانی، دو برابر تغییر طول ناشی از بارگذاری استاتیک است. بنابراین، ضریب ضربه در این شرایط 2 خواهد بود. پس از رسیدن به تغییر طول ماکسیمم (δ_max)، انتهای میله به سمت بالا حرکت کرده و چندین بار به سمت پایین و بالا نوسان می‌کند. این فرآیند تا لحظه ثابت ماندن میله در تغییر طول استاتیک (δ_st) ادامه می‌یابد.

نکاتی در مورد تحلیل بارگذاری ضربه‌ای

تحلیل‌های بالا بر اساس فرض عدم هدر رفت انرژی در حین بارگذاری ضربه‌ای صورت گرفتند. در واقعیت، هدر رفت انرژی همیشه وجود دارد و در اکثر مواقع به صورت گرما و تغییر شکل‌های محلی ماده رخ می‌دهد. به همین دلیل، مقدار انرژی جنبشی سیستم بلافاصله پس از رخ دادن ضربه کمتر از انرژی جنبشی پیش از رخ دادن ضربه است. از این‌رو، تحت این شرایط انرژی کمتری به انرژی کرنشی تبدیل می‌شود. در نتیجه، جابجایی واقعی انتهای میله کمتر از مقدار پیش‌بینی‌شده در تحلیل‌های صورت گرفته با فرضیات ساده‌سازی خواهد بود.

در تحلیل‌های صورت گرفته فرض کردیم که تنش‌های ایجاد شده درون میله در محدوده الاستیک خطی (زیر حد تناسب) قرار دارند. اگر مقدار تنش ماکسیمم (σ_max) از حد تناسب بیشتر شود، تحلیل بارگذاری ضربه‌ای پیچیده‌تر خواهد شد؛ چراکه در این وضعیت، تغییر طول میله نسبت به نیروی محوری متناسب نخواهد بود. علاوه بر این، عوامل دیگری نظیر موج‌های تنش، میرایی و نقص‌های موجود بر روی صفحات اتصال نیز بر روی نتایج تحلیل تأثیرگذار هستند. بنابراین، باید به خاطر داشته باشیم که تمام روابط ارائه شده در این مقاله، بر اساس فرضیات ایدئال به دست آمده‌اند. به همین دلیل، نتایج حاصل از این روابط را می‌توان تنها به عنوان یک تقریب خام از شرایط واقعی در نظر گرفت.

موادی که شکل‌پذیری قابل توجهی را پس از حد تناسب از خود به نمایش می‌گذارند، مقاومتشان در برابر بارگذاری ضربه‌ای بسیار بیشتر از مقاومت مواد شکننده است. به علاوه، وجود شیار، حفره و دیگر مصادیق تمرکز تنش در میله باعث کاهش مقاومت آن در برابر ضربه می‌شود. در این حالت، اعمال یک شوک کوچک نیز می‌تواند باعث رخ دادن شکست شود.

مثال‌های کاربردی

در انتها برای آشنایی بهتر با کاربرد روابط تنش و کرنش برشی در مسائل واقعی، به تشریح چند مثال کاربردی می‌پردازیم.

مثال 1

یک میله مدور منشور با طول 2 متر، قطر 15 میلی‌متر و مدول الاستیسیته 210 گیگاپاسکال را در نظر بگیرید (شکل زیر). این میله به صورت عمودی از انتهای بالایی خود به یک تکیه‌گاه وصل شده است. یک حلقه لغزنده با جرم 20 کیلوگرم از ارتفاع 150 میلی‌متری (نسبت به فلنج) رها می‌شود.

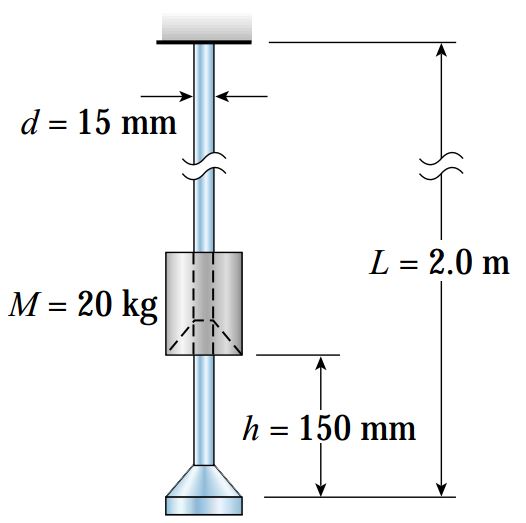
• الف) تغییر طول ماکسیمم میله در اثر اعمال ضربه و ضریب ضربه مرتبط با آن را محاسبه کنید.
• ب) تنش کششی ماکسیمم در میله و ضریب ضربه مرتبط با آن را محاسبه کنید.

نحوه قرارگیری حلقه و میله در شکل بالا، مشابه مثالی است که در مقاله مورد تحلیل قرار گرفت. از این‌رو، می‌توانیم از روابط δ_max و σ_max برای حل این مثال استفاده کنیم.

الف) تغییر طول ماکسیمم. اولین قدم برای تعیین تغییر طول ماکسیمم (δ_max)، محاسبه تغییر طول استاتیک میله (δ_st) با توجه به وزن حلقه است. به این ترتیب، با در نظر گرفتن رابطه W=Mg برای وزن حلقه، تغییر طول استاتیک به صورت زیر خواهد بود:

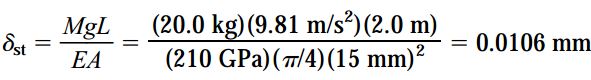
با حل رابطه بالا می‌توان مشاهده کرد که:

اگر مقدار نسبت به دست آمده را در رابطه δ_max جایگذاری کنیم، مقدار تغییر طول ماکسیمم به دست می‌آید:

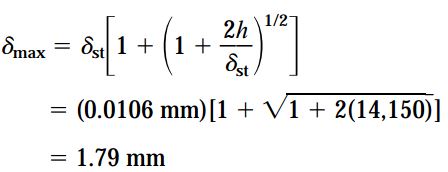
ارتفاع سقوط حلقه (h) نسبت به میزان تغییر طول استاتیک (δ_st) بسیار بزرگ است. به همین دلیل، اگر عبارات 1 را از رابطه بالا حذف کنیم، δ_max تغییر چندانی نخواهد داشت:

ضریب ضربه با نسبت δ_max به δ_st برابر است:

نتیجه به دست آمده نشان می‌دهد که در صورت اعمال بارهای مشابه، تأثیر بارگذاری دینامیک می‌تواند بسیار بیشتر از بارگذاری استاتیک باشد.

ب) تنش کششی ماکسیمم. تنش ماکسیمم (σ_max) ایجاد شده در اثر سقوط حلقه از رابطه زیر به دست می‌آید:

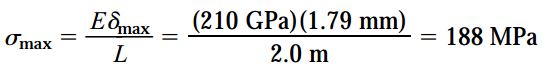
مقادیر تنش ماکسیمم و تنش استاتیک (σ_st) باید با یکدیگر مقایسه شوند:

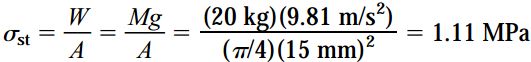
نسبت σ_max به σ_st با 169=188/1.11=Impact Factor برابر است. برابر این نسبت با ضریب ضربه محاسبه شده بر اساس مقادیر تغییر طول برابری می‌کند. نتیجه به دست آمده کاملاً قابل انتظار بود چراکه مقادیر تنش و تغییر طول با یکدیگر متناسب هستند.

مثال 2

میله افقی AB با طول L را در نظر بگیرید. بلوکی به جرم M به صورت افقی و با سرعت v به انتهای آزاد این میله ضربه وارد می‌کند.

• الف) حداکثر کاهش طول میله در اثر این ضربه و ضریب ضربه مربوط به آن چقدر است؟
• ب) حداکثر تنش فشاری و ضریب ضربه مرتبط با آن چقدر است؟

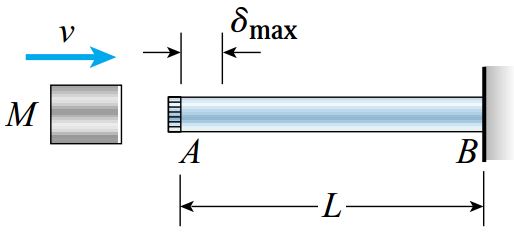
نحوه بارگذاری در این مثال با مثال قبلی کاملاً متفاوت است. بنابراین، برای حل این مسئله باید از روش تحلیلی جدید بر اساس اصل بقای انرژی استفاده کنیم.

الف) کاهش طول ماکسیمم میله (δ_max). به منظور تحلیل این مسئله، فرضیات ارائه شده در این را به کار می‌گیریم. بنابراین، از هدررفت انرژی در حین بارگذاری صرف نظر می‌کنیم. با توجه به این فرض، تمام انرژی جنبشی بلوک به طور کامل به انرژی کرنشی میله تبدیل خواهد شد.

انرژی جنبشی بلوک در لحظه برخورد با میله از رابطه Mv²/2 به دست می‌آید. انرژی کرنشی میله در هنگام رسیدن به تغییر طول ماکسیمم نیز از رابطه EAδ_max/2L تعیین می‌شود. طبق اصل بقای انرژی داریم:

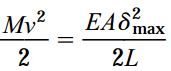
با حل رابطه بالا نسبت به δ_max خواهیم داشت:

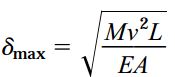
برای تعیین ضریب ضربه، باید جابجایی استاتیک انتهای میله را نیز محاسبه کنیم. در این مثال، جابجایی استاتیک با کاهش طول میله بر اثر اعمال بار فشاری حاصل از ضربه بلوک بر روی میله برابر است:

بنابراین، ضریب ضربه برابر است با:

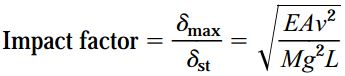
ب) تنش فشاری ماکسیمم در میله (σ_max). میزان تنش ماکسیمم در میله با استفاده از مقدار تغییر طول ماکسیمم قابل محاسبه است:

تنش استاتیک (σ_st) در میله با رابطه W/A یا Mg/A تعیین می‌شود. مقدار ضریب ضربه بر اساس تنش نیز با ضریب ضربه بر اساس تغییر طول برابر خواهد بود.

^^